基于尖點突變理論的軟巖棄渣路堤局部穩定性分析

鞠興華，楊曉華，張莎莎

(1.濰坊學院建筑工程學院，山東 濰坊 261041;2.長安大學公路學院，陜西 西安 710064)

軟巖在我國分布廣泛。隨著經濟的快速發展，軟巖地區的公路建設日益增加，但其“似土非土、似石非石”的特性也帶來諸多工程問題。目前，軟巖棄渣在路基填筑中的合理性問題已被廣泛關注[1-2]。鑒于軟巖具有水理性差、強度低、成分復雜等特征，許多學者對其在路基填筑中的可行性和適用性進行了深入研究。張靜波等[3]利用動三軸試驗分析了軟巖填料在干濕循環條件下的動力特性，為工程施工提供了的參考依據；毛雪松等[4]探討分析了不同顆粒級配及水泥摻入量對路基填料CBR值的影響，確定了兩者的最佳組合；宋楊等[5]對路基壓實度的影響因素進行了研究，得出了施工參數與壓實度間的影響關系，合理指導了實際施工；毛雪松等[6-7]對以千枚巖作為路基填料的施工工藝進行了設計，并根據現場實測結果進行了技術改良；趙德新[8]、詹永祥等[9]在填筑材料性能研究的基礎上，探討了不同填筑參數的組合施工效果，并提出了相應的控制措施，為類似軟巖路基的填筑施工積累了經驗。上述研究取得了一定的成果，但多偏重于路基填料的工程性質分析，未涉及路基填筑后的穩定性評價，也未涉及尖點突變理論的應用；同時，不同地區的軟巖性質具有差異，加之地質環境條件不盡相同，因此需對不同地區的軟巖路基填筑進行針對性的研究。

成武高速(成縣—武都)共設計30余座隧道，巖性以紅層軟巖為主，伴隨隧道開挖，將會產生大量軟巖棄渣。由于工程地處長江上游環境保護區，工程區的水土保持、生態保護具有嚴格要求，其棄渣存放面臨多種問題，如耕地占用、破壞地貌景觀等；且成武高速地處隴南山嶺重丘區，交通較為不便，使得路基填料取土困難，嚴重影響工程的經濟效益。因此，若能將隧道棄渣用于路基填筑，將會大大降低投資成本，具有很好的實用價值。綜合上述，本文以成武高速公路為工程實例背景，分析了路基填筑材料的工程特性；結合路基沉降監測數據，分析路基填筑后的穩定性及其發展趨勢。

1 工程概況

成武高速公路是甘肅省境內的重點建設項目之一，具有特殊的作用和地位。該高速公路主要涉及9個鄉鎮，起點位于隴南市成縣，終點位于武都區城郊鄉，設計行車速度80 km/h，路基寬24.5 m，全長為92.04 km，其中包含4.4 km的二級公路連接線[10-12]。

如前所述，成武高速公路包含30余座隧道，巖性以泥質粉砂巖和粉砂質泥巖為主，紅色，屬紅層軟巖，具不等互層結構，親水性強、透水性弱、強度低(一般小于30 MPa)、軟化性強，且失水后易崩解；同時，巖層層面遇水易滑動，巖體層面之間抗剪強度低，特別是層面之間含水后易產生層間滑動。

2 工程特性分析

2.1 篩分試驗結果

根據隧道開挖過程，區內棄渣具有明顯的差異性特征，主要體現在顆粒成分、顏色及粒徑等方面。為綜合、全面分析區內棄渣的工程特征，該文以顆粒成分、顏色及粒徑等為劃分指標，將棄渣劃分為三類(Ⅰ類、Ⅱ類、Ⅲ類)，并對三類棄渣進行試驗分析。其中，篩分試驗結果表明，Ⅰ類棄渣屬巨粒混合土，紅褐色，巨粒土含量為15%～50%，不均勻系數為12～30，曲率系數為0.82～4，波動性較大，但平均結果的級配較好；Ⅱ類棄渣屬礫類土，紅色，礫類土質量占比大于總質量的50%，不均勻系數5～8，曲率系數0.5～0.8，波動性相對較小，級配較好；Ⅲ類棄渣屬巨粒土，灰色，巨粒組含量間于50%～75%，不均勻系數6～10，曲率系數0.5～1.28，級配較好。對比三類棄渣的篩分結果，得出不同棄渣的級配雖具有一定的差異，但整體級配分布區間一致，均屬級配較好，基本符合路基填筑要求。

2.2 擊實試驗結果

由于成武高速泥質軟巖棄渣中的大尺寸顆粒相對較多，有些粒徑已經超過規范規定的標準重型擊實試驗的試桶要求，為了使試驗結果更加可靠，研制了適用于大顆粒的大型擊實試驗。其中，標準重型擊實試驗的錘底直徑5 cm，錘質量4.5 kg，落高45 cm，試樣高度12 cm，試樣體積2 177 cm3；大型擊實試驗擊錘直徑5 cm，擊實錘重量4.5 kg，擊錘下落高度45 cm，所用試模尺寸直徑30 cm，高度35.4 cm，體積25 000 cm3。結合前述級配分析結果，Ⅰ類和Ⅲ類棄渣采用大型擊實試驗，Ⅱ類棄渣采用標準擊實試驗，三類棄渣的擊實試驗結果如表1所示。可以看出Ⅰ類棄渣的最優含水率最高，Ⅲ類棄渣的最大干密度最大，且三者的平均最優含水率為6.5%，平均最大干密度為2.27 g/cm3。同時，結合現場鉆孔取樣后的巖石試樣數據，兩類原巖的天然密度為2.42～2.55 g/cm3，少量可達2.6 g/cm3，而含水率則為3.0%～4.5%。與室內擊實試驗成果對比可知，路基填筑后的最佳密度要適當小于原巖狀態的密度，這與開挖后的松散及填筑工藝相關。

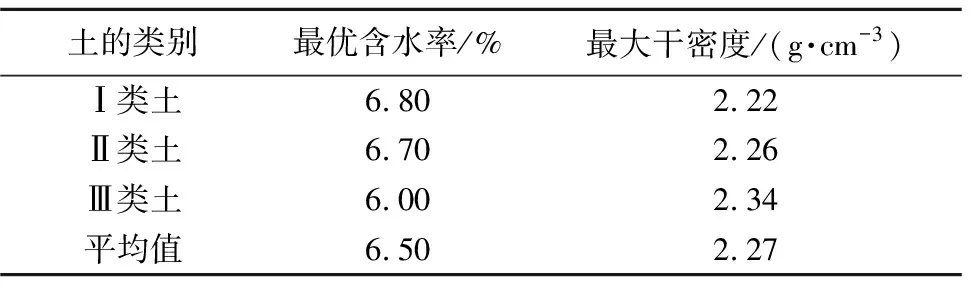
表1 擊實試驗結果

2.3 CBR試驗結果

在前述擊實試驗的基礎上，按照最優含水率制備CBR試驗試樣。在CBR試驗過程中，需進行浸水膨脹，該過程為：在試件面部鋪設薄濾紙，并將其放置于多孔板上，用拉桿固定試樣筒和多孔板；對試樣筒進行倒轉，在其另一面也放設濾紙，并在該面上放置多孔頂板及4塊荷載板，每塊荷載板1.25 kg；將整個裝置放入水槽中，并安裝好測定膨脹量的裝置，在初始讀數讀取后，向水槽內注水，水面應高出試件25 mm，浸泡時間為96 h；量測浸水后試件的高度，計算膨脹量；卸除膨脹量測定裝置，取出試樣筒，吸去試件頂面的水，靜置15 min后卸下荷載塊、多孔頂板和多孔底板、濾紙，稱試樣筒和試件總質量，計算試樣含水率和干密度的變化。最后，采用微機控制電子式萬能試驗機進行貫入試驗。

在試驗過程中，對貫入深度2.5 mm和5 mm均進行試驗。根據試驗及統計，得到CBR試驗結果(表2)。

表2 CBR試驗成果

在不同貫入深度條件下，均以Ⅲ類棄渣的CBR值相對更大，說明Ⅲ類棄渣的路基填筑性質相對更佳；同時，在各組試驗中，對比貫入深度為2.5 mm和5 mm時的CBR值，得出前者均小于后者，因此，以貫入深度為5 mm時的試驗結果為采用值，且三類土的CBR5.0值均滿足高速公路填筑路堤的強度要求。

綜合上述對棄渣工程特性的分析，得出成武高速的軟巖棄渣具有較好的工程特性，可作為路基填料，但是在路基填筑過程中，應嚴格控制含水率，建議將含水率控制在6.5%左右。

3 穩定性現狀評價

3.1 基本變形特征

在完成路基填筑以后，為掌握其沉降特征，進行了路基沉降監測，并利用尖點突變理論分析局部路基穩定性的現狀。監測斷面布置在成武高速第四標段C匝道，共布設兩個監測斷面，斷面布置如圖1所示，兩斷面水平間隔120 m；同時，每個監測斷面共布置11個監測點，兩斷面的監測點布置情況圖2所示。在監測過程中，監測頻率為1次/周，監測項目為沉降監測。

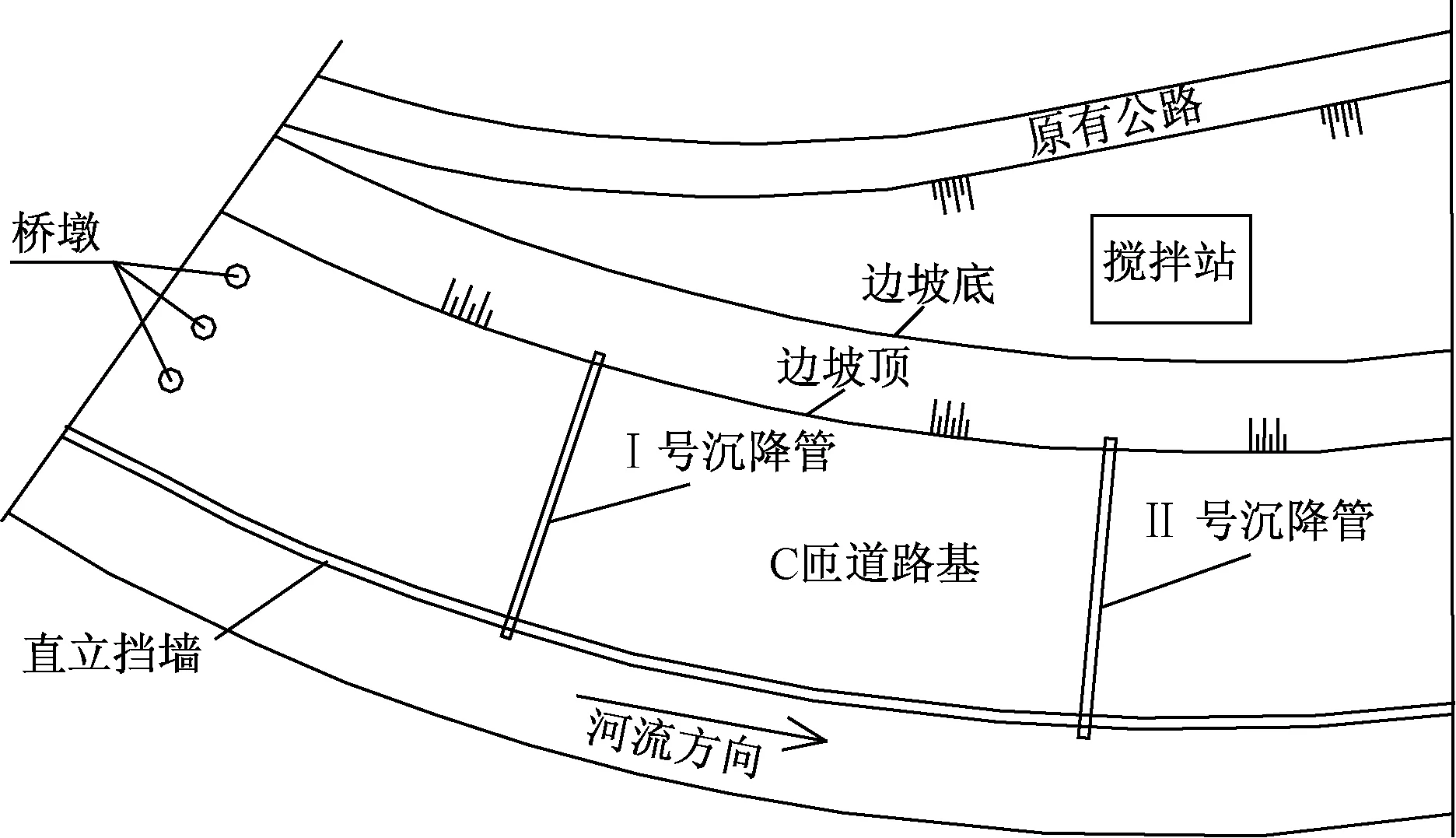
圖1 監測平面布置示意圖

圖2 監測斷面布置示意圖

根據現場監測，共獲得21期(147 d)的監測數據。Ⅰ號監測斷面的最大沉降量發生在6號監測點，沉降值為71.3 mm，位于監測斷面中部；最小沉降量發生在1號監測點，沉降值為16.9 mm，位于路基靠邊坡一側。Ⅱ號監測斷面的最大沉降量發生在7號監測點，沉降值為61.4 mm，位于監測斷面中部；最小沉降量發生在1號監測點，值為26.4 mm，位于路基靠邊坡一側。

對兩斷面相應監測點的沉降變形進行對比，得到圖3。由圖3可知，路基沉降變形以中心處的沉降量相對更大，斜坡側的沉降量相對較少，即路基沉降具不均勻特性；對比Ⅰ、Ⅱ監測斷面在相應監測點處的沉降量可知，Ⅰ號監測斷面的沉降量要略大于Ⅱ號監測斷面的沉降量，說明隨路基深度的增加，沉降量相應減小。

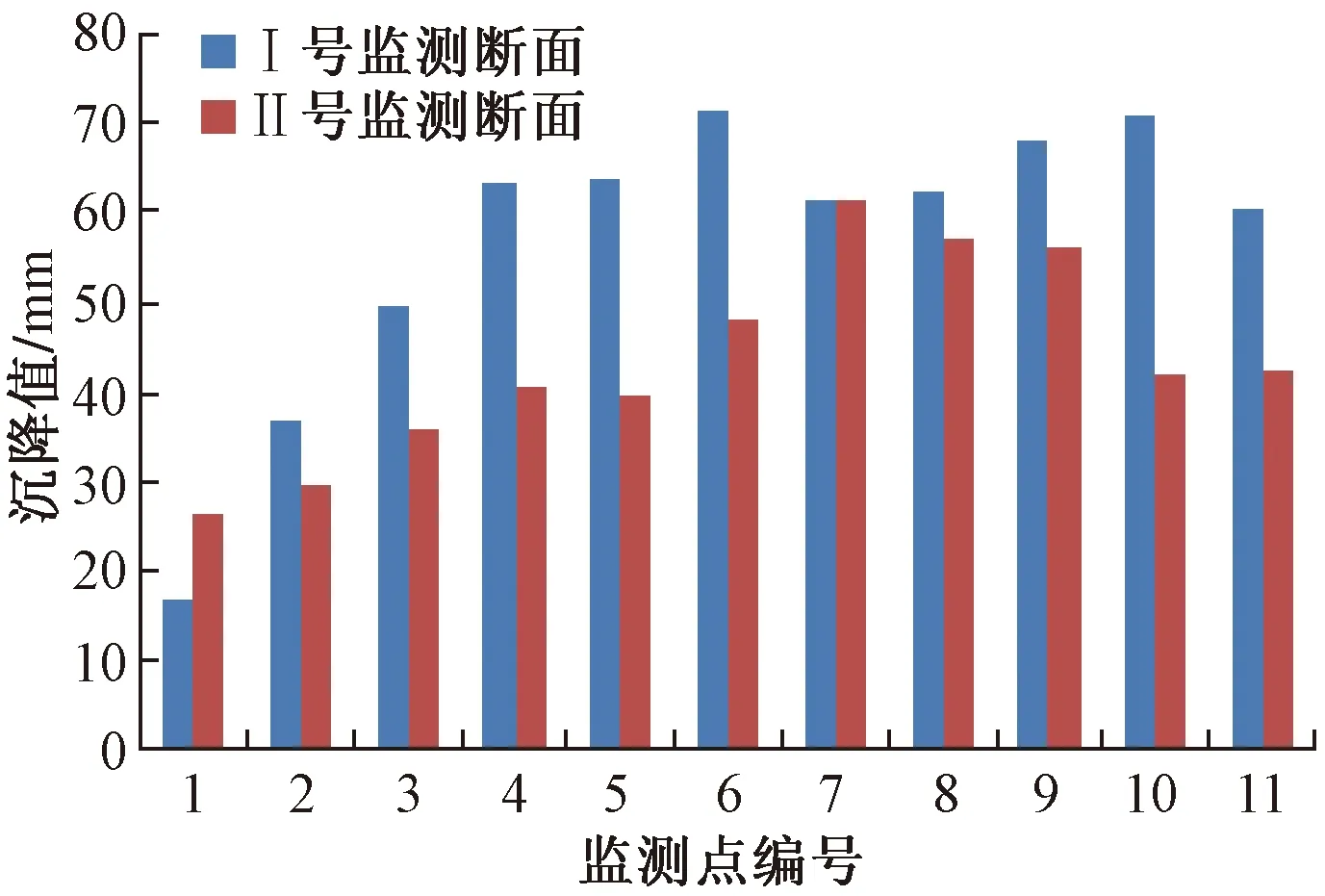
圖3 兩監測斷面的沉降對比圖

3.2 穩定性評價

根據路基填筑效果分析，得出路基整體穩定性滿足設計要求，但因填料遇水易崩解等特性，在后期運營過程中，路堤內部填料因水的作用可能會出現崩解，導致局部的變形失穩。為進一步分析路基局部的穩定性特征，本文基于局部現場監測成果，以尖點突變理論中的突變特征值為評價指標，判斷路基填筑后的穩定性。

尖點突變理論的研究重點是事物穩定與非穩定間的轉換問題，對路基穩定性評價具有一定的適用性[13]。結合尖點突變理論的基本原理，先利用數值擬合來構建勢函數，即采用Matlab擬合工具箱，對路基沉降數據進行四次多項式擬合：

Yt=a0+a1t+a2t2+a3t3+a4t4

(1)

式中：Yt——t時刻對應的擬合值；

ai(i=0，1，2，3，4)——擬合參數。

由于式(1)并非尖點突變理論的標準形式，需進行變換處理，且將變換方式確定為Tschirhaus變換，即令A=a3/4a4，t=x-A，并將其帶入式(1)進行轉化，得：

fx=b4x4+b2x2+b1x+b0

(2)

式中：fx——變換函數；

bi(i=0，1，2，4)——變換參數。

同時，參數a和b間存在如下矩陣變換關系：

(3)

對式(2)兩側同除b4，即可得到尖點突變理論的標準函數：

Ux=x4+μx2+vx+c

(4)

式中：Ux——標準函數；

μ、ν——突變特征參數。

兩突變特征參數可根據下式進行求解：

(5)

(6)

基于兩特征參數，可求得突變特征值：

Δ=8μ3+27v2

(7)

根據上述原理，提出以突變特征值為評價指標，判斷路基沉降的穩定性，其判據為：當Δ<0時，路基處于不穩定狀態；當Δ=0時，路基處于臨界平衡狀態；當Δ>0時，路基處于穩定狀態。另外，當Δ>0時，Δ值可進一步評價路基的穩定程度，即Δ值越接近于零，穩定性越好[14]。

同時，在尖點突變分析過程中，選取兩斷面中沉降量最大的監測點為分析對象，即分析數據來源于Ⅰ號監測斷面的6號監測點和Ⅱ號監測斷面的7號監測點。

首先，對兩監測點的所有監測樣本進行尖點突變分析，以掌握其整體穩定性，且經Matlab的擬合工具箱擬合，得6號監測點的四次多項式擬合函數為：

yⅠ=-1.132×10-6t4+3.977×10-4t3-4.474×10-2t2+2.465t+1.812×10-13

根據擬合結果，6號監測點的擬合度為0.982 7，具較好的擬合效果，保證了后續分析的有效性。結合尖點突變理論的基本原理，對突變特征參數和特征值進行求解：

μⅠ=-4.351×104；νⅠ=-2.317×105

則

ΔⅠ=7.903×1011>0

根據上述計算，得到第Ⅰ斷面6號監測點的突變特征值大于零，說明該監測點處于穩定狀態。

類比上述，對第Ⅱ斷面的7號監測點進行尖點突變分析，經擬合，得其四次多項式擬合函數為：

yⅡ=-8.808×10-7t4+3.193×10-4t3-3.951×10-2t2+2.124t+1.498×10-13

在7號監測點的擬合過程中，其擬合度為0.9879，較趨近于1，說明該監測點的擬合效果也較好。同時，也對該監測點的突變特征參數和特征值進行求解：

μⅡ=-4.423×103；νⅡ=-2.358×105

則

ΔⅡ=8.085×1011>0

根據計算結果，得到第Ⅱ斷面7號監測點的突變特征值也大于零，說明該監測點也處于穩定狀態。

對比兩監測點的整體穩定性分析結果，得到兩者均處于穩定狀態，且ΔⅡ>ΔⅠ，說明6號監測點的穩定性相對更高。

其次，為掌握路基穩定性隨時間持續的變化特征，再將監測樣本劃分為1-7周期、1-14周期、1-21周期三個階段，并對各階段進行尖點突變分析，結果如表5和6所示。

表5 6號監測點在不同階段的穩定性分析結果

表6 7號監測點在不同階段的穩定性分析結果

由表5和6可知，兩監測點在不同階段的突變特征值均大于零，說明路基始終處于穩定狀態，且隨時間持續，突變特征值不斷減小，路基穩定性增加。

綜合上述，整體分析和分階段分析均得出路基處于穩定狀態，驗證了路基填料的適用性，為類似工程施工積累了經驗。

4 穩定性發展趨勢分析

通過構建粒子群優化極限學習機(PSO-ELM模型)來實現路基沉降的變形預測，進而判斷路基穩定性的發展趨勢[15-16]。極限學習機(Extreme Learning Machine，ELM)是一種新型智能模型，具有較高的學習速度和泛化能力，適用于非線性預測。若訓練樣本為(xi,ti)，且總個數為N，則可將極限學習機的網絡模型表示為：

(8)

式中：yi——第i個節點處的預測值；

xi——第i個節點處的預測輸入值；

K——隱層節點數；

g(x)——激勵函數；

βi——隱層與輸出層間的連接權值；

wi——輸入層與隱層間的連接權值；

bi——隱層偏置。

極限學習機在相應參數設置前提下，可實現預測結果到期望結果的零誤差逼近，即

(9)

根據訓練樣本可構建N個方程，并將其表示為矩陣形式：

T=Hβ

(10)

式中：T——期望輸出矩陣；

H——隱層輸出矩陣；

β——權值矩陣。

上式可等價于求解H=βT的最小二乘解，即需求解β′矩陣：

β′=H+T

(11)

式中：H+——H矩陣的廣義逆矩陣。

在極限學習機的應用過程中，隱層節點數一般小于訓練樣本數，易造成復共線性問題，進而導致輸出結果的隨機波動，造成預測結果的穩定性不足。因此，為克服上述問題，該文提出利用粒子群算法優化極限學習機的權值矩陣和隱層偏置。

粒子群算法可將尋優參數看作為空間粒子的屬性，通過不斷迭代來更新粒子速度和位置，進而得到尋優目標的全局最優值。結合該文實例特點，將權值矩陣和隱層偏置的優化過程分述如下：

①隨機產生一個粒子群，并對群中每個粒子賦予參數屬性，即將權值矩陣和隱層偏置作為粒子屬性，并將種群規模設置為30，慣性權值設置為1，學習因子設置為2，最大迭代次數為600 次，實現了粒子群的初始化。

②按下式求解各粒子的適應度值：

(12)

式中：fi——第i個粒子的適應度；

f(xi)——第i個節點處的預測值；

yi——第i個節點處的樣本值。

③以適應度最小為原則，對比粒子群中所有粒子的適應度值，確定其中的最佳粒子。當最佳粒子的適應度值滿足期望要求時，則停止迭代，最佳粒子的屬性參數即為最優權值矩陣和隱層偏置；反之，改變粒子的位置和速度，并重新求解粒子的適應度值，直至達到期望值或達到設定的迭代次數。

在預測過程中，對Ⅰ號監測斷面的6號監測點和Ⅱ號監測斷面的7號監測點均進行預測。將訓練樣本設置為1～17周期，18～21為驗證樣本，且對22～24周期進行外推預測。通過預測，得兩監測點的預測結果如表7～8所示。

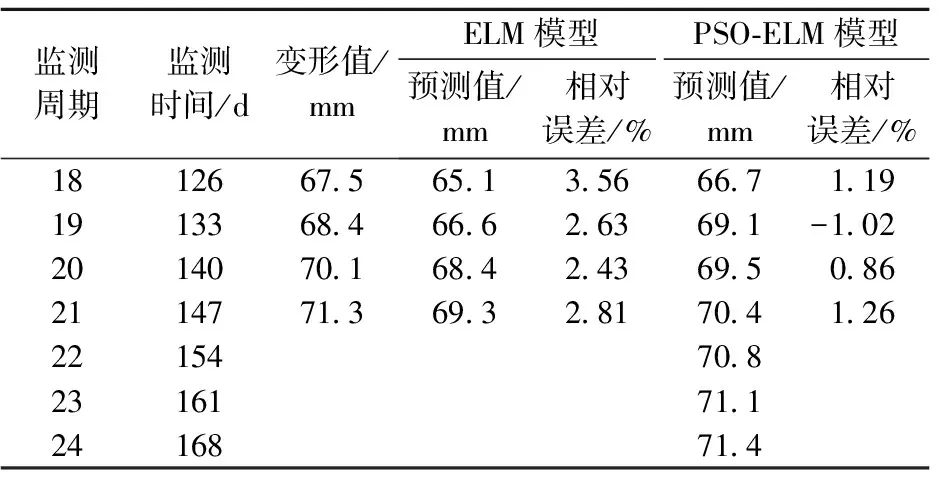
表7 6號監測點的預測結果

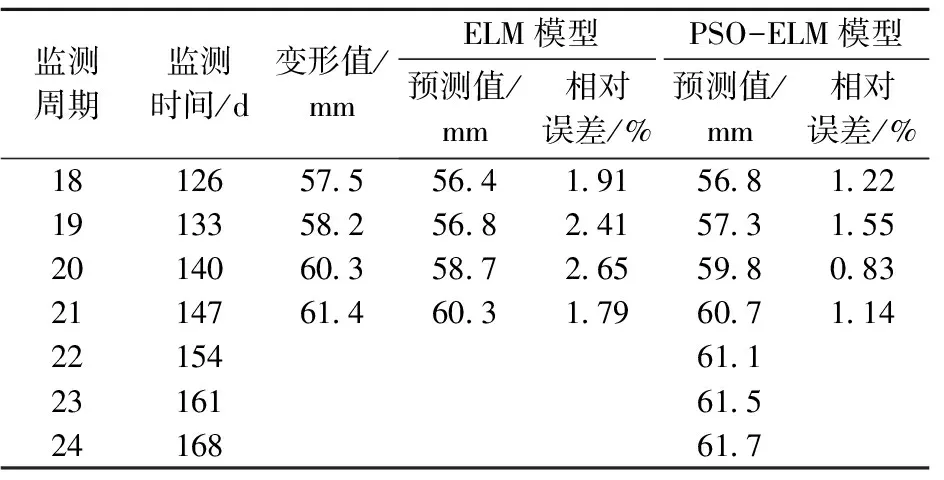
表8 7號監測點的預測結果

對比優化前后各監測點在相應節點處的預測效果可知，經粒子群算法的參數優化，有效提高了預測精度，驗證了參數優化的有效性和必要性；在6號監測點的最終預測結果中，最大相對誤差1.26 %，最小相對誤差為-1.02 %，平均相對誤差0.57 %，預測精度較高，滿足期望要求，且外推預測表明，該監測點的變形值將會繼續增加，但增加速率較小，趨于穩定；在7號監測點的最終預測結果中，最大相對誤差1.55 %，最小相對誤差為0.83 %，平均相對誤差1.18 %，也具有較高預測精度，進一步驗證了該文預測模型的有效性，且其外推預測變形值也呈小速率增加趨勢。

根據上述，得出路基變形仍將進一步增加，但增加速率均較小，說明路基變形趨于穩定，且其穩定性發展趨勢也趨于穩定。

5 結論

(1)通過多種工程性質試驗，得出成武高速各類棄渣級配均屬較好，可作為路基填料，但是在路基填筑過程中，應以最優含水率進行嚴格控制。

(2)根據路基沉降監測，最大沉降量為71.3 mm，且Ⅰ號監測斷面的最終平均沉降量為56.77 mm，而Ⅱ號監測斷面的最終平均沉降量為43.51 mm，說明隨路基深度的增加，沉降量相應減小。

(3)在路基整體穩定性分析中，6號監測點和7號監測點的突變特征值均大于零，判斷兩監測斷面均處于穩定狀態，且以Ⅱ監測斷面的穩定性相對更高。

(4)在路基穩定性的分階段分析中，路基不同階段的突變特征值也大于零，得出路基始終處于穩定狀態，且隨時間持續，突變特征值具減小趨勢，認為路基穩定性隨沉降時間的持續具有增加趨勢。

(5)粒子群算法可有效提高極限學習機的預測精度，且PSO-ELM模型能很好實現路基的變形預測，得出路基變形仍將進一步增加，但增加速率均較小，即穩定性發展趨勢趨于穩定。