高中函數解題思路的多元化

江蘇省江陰市第一中學 劉麗麗 顧靜凌

一、函數解題思路多元化的重要性簡析

高中函數是初中函數的延伸和拓展，其深入性和復雜性大幅增強，對學生的數學思維能力要求更高。一般來說，從初中函數題目的特征來看，其思路簡明且較易想到，單一化解題思路占據主導，但高中函數題目則解題難度偏大，大多較為復雜且有著多種思路，單一思路解題不僅效率差，且正確率低，因而促進學生解題思路多元化向來是高中函數教學的重要一環。具體來說，要能夠使學生切實轉變函數解題思維，思考習慣和思路認知上由一元轉變為多元，并能夠在實際解題中依據自身特點快速找到適合自己的思路和解法，從而提高解題效率和正確率。而要達到這樣的效果，就需要教師在習題教學中精選典型例題，通過有效的引導和強調提高學生的發散性思維水平和創新性思維水平。

二、培養學生發散思維與創新思維

高中函數題的順利解答有賴于弄清題目的結構和條件（尤其是隱含條件）間的有機關系，這往往需要學生從多個角度加以思考，從不同的切入點嘗試建立已知條件和所求結論之間的聯系，若只僅限于一種思路，則容易受到定式思維的影響，難以快速而準確地解答題目。而發散性思維正是要求解題者從不同的角度分析問題，它是解題思路多元化的基礎性思維方式，但僅有這個條件還是不夠的，學生還必須具備一定的創新性思維，否則就無法產生創新性的思路和解法。事實上，發散思維和創新思維是相輔相成、不可分割的關系，前者為“體”，后者為“用”，學生只有兩者兼具，才能真正形成合格的函數多元化解題能力。而要提升學生的發散思維和創新思維水平，就需要教師在平時的習題教學中注重選擇較為典型的題目，引導學生從不同的角度分析，進而掌握各種思路解法的創新點，長期使學生經歷這樣的思維訓練過程，就能在潛移默化中有效促進學生發散思維和創新思維的發展。下面我們來看一道具體例題：

該題是2018 年高考全國一卷理科21 題第二問，有“直接換元法”“對數均值不等式法”“洛必達法則法”三種解法，我們先看一下三種解法的解題過程：

解法一：直接換元法

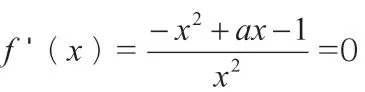
解法二：對數均值不等式法

解法三：洛必達法則法

明確了三種解法的過程并加以對比后就不難發現，解法一思路簡明，常規性較強，多數考生一般首先想到的都是“直接換元法”，但解法二的簡便性和技巧性則更為突出一些，解法三比較繁復，需要反復設函數求導，通過層層傳導證明函數的單調性，但其思路上亦有可取之處。大體來說，三種思路各有特點和優勢，在具體的剖析過程中，教師要能夠使學生切實掌握每種思路，并明了每種思路的特點，使學生在深度思考中提升思維水平，促進解題思路的多元化發展。