基于信噪比-虛擬力算法的水下傳感網絡節點移動策略研究*

楊海波,趙克華,祝云凱

(1.浙江樹人大學信息科技學院,杭州 310015;2.浙江杭佳科技發展有限公司,杭州 310010)

水下無線傳感網絡(Underwater Wireless Sensor Networks,UWSN)是將低能耗、通信距離受限的節點部署在指定水域中,利用節點的自組織能力組網,對指定區域內的信息進行采集并完成相應的數據整理[1]。UWSN在海洋資源勘探、海洋環境監測以及海洋軍事領域有廣泛且重要的用途,已經引起工業界、學術界以及軍事界的極大關注。

近年來,隨著各國發展海洋經濟熱潮的不斷興起,UWSN已經成為無線傳感器網絡的熱點研究領域。區別于傳統無線傳感網絡(Wireless Sensor Networks,WSN),UWSN需要監測三維水域環境。由于水下環境復雜多變且僅能依靠衰落較快的聲波信號傳輸信息,使得許多傳統WSN的方法并不適用于UWSN[2]。尤其水下節點移動策略直接關系網絡的節點能量、通信帶寬、監測信息的準確性,成為UWSN眾多研究方向的首要待解決問題。

虛擬力模型(Virtual Force Algorithm,VFA)是解決WSN節點移動策略的主要方法之一[3-7]。傳統虛擬力模型通過采集鄰居節點的信息,并與事先確定的閾值進行比較判斷,確定節點所受斥力或者引力的大小及方向[3]。網絡中的節點將根據所受力的大小及屬性(引力或斥力)進行移動。李明等[4]以網絡覆蓋率最大為優化目標函數,提出一種解決異構WSN覆蓋問題的虛擬力導向差分優化算法。在該算法中,節點間距離被用于關鍵指標并以指數函數形式建立虛擬力模型。區別于傳統線性函數形式的虛擬力模型,指數函數能夠增加算法收斂速度,減少計算用時。魏連鎖等[5]對傳統虛擬力模型進行改進,以網絡節點的鄰居節點數量以及到鄰居節點的距離兩項因素作為關鍵指標并以指數函數形式建立虛擬力模型,提出一種適用于WSN的錨節點移動策略。區別于傳統虛擬力模型,采用雙項指標構建指標函數有效地解決節點移動策略的多目標優化問題。傳統虛擬力模型在UWSN中的應用主要體現于節點部署策略,尤其是提高網絡覆蓋率。由于UWSN特殊性使得難以在網絡中實現確定性節點部署,虛擬力模型便可以實現節點動態部署。羅強等[6]在UWSN中引入虛擬力的概念作為節點部署的重要策略,以提高節點初始隨機部署后的覆蓋率。首先,將節點隨機散布于UWSN;然后,通過計算節點間距離從而確定所受力的大小及方向。王軍等[7]基于三維網格劃分與虛擬力模型,提出了一種適用于UWSN的節點部署策略。在文章中,采用節點間距離作為關鍵指標并以線性函數形式構建虛擬力模型,從而實現UWSN節點動態部署策略。

綜上所述,虛擬力算法制定的節點移動策略多以提高網絡整體覆蓋率為目標,而較少考慮網絡吞吐量、網絡生存時間等重要因素。本文基于傳統虛擬力模型,提出一種以信道比與節點度雙因素作為關鍵指標的虛擬力算法,并據此制定UWSN節點移動策略(SINR Virtual Force Algorithm,SVFA)。

表1 幾種虛擬力構造方式對比表

1 節點模型與信道模型

1.1 節點模型

假設在UWSN中部署N個節點,且每個節點都具備相同的覆蓋半徑Rcov。在真實環境中,傳感器可以監測以其自身為球心,以Rcov為半徑的圓球內部數據信息。同時,每個節點都具備相同的通信半徑Rcom,傳感器可以與以其自身為球心,以Rcom為半徑的圓球內部的其他節點進行通信業務。為了便于描述UWSN節點間的連通狀況,引入一個0-1連通矩陣T=(tij)N×N,矩陣元素含義如下所示:

位置i與位置j的兩個傳感器節點三維坐標分別表示為(xci,yci,zci)與(xcj,ycj,zcj),i=1,2,…,N;j=1,2,…,N。連通矩陣元素計算方式如下:

(1)

定義本地節點通信范圍內的鄰居傳感器節點數量為節點度[8]。因此,位置i的傳感器節點度ndi計算公式如下所示:

(2)

覆蓋率是UWSN節點部署與節點移動策略非常關注的一項指標。為描述UWSN覆蓋狀況,可以將網絡離散成K×M×L的三維長方體網格。覆蓋矩陣維度P為網絡格點總數,P=(K+1)×(M+1)×(L+1)。引入覆蓋矩陣F=(fij)N×P,矩陣元素含義如下所示:

位置i的傳感器節點與位置j的探測點三維坐標分別表示為(xci,yci,zci)與(xgj,ygj,zgj),i=1,2,…,N;j=1,2,…,P。覆蓋矩陣元素計算方式如下:

(3)

通過覆蓋矩陣F=(fij)N×P可得網絡中任何一個格點被覆蓋的情況K=(ki)1×P,矩陣元素的計算方法如下:

(4)

將UWSN的覆蓋效率定義為指定區域被覆蓋格點數與網絡格點總數之比[9]。網絡覆蓋效率指標g可以表達如下:

(5)

1.2 信道模型

UWSN節點之間正常通信不僅要求滿足連通性指標tij=1,還要滿足鏈路信噪比閾值要求[10]。因此,需要考慮信息傳輸的信道模型。當發送節點S向目的節點D發送信息時,處于目的節點D通信半徑內的其他節點R1與R2將對節點S與D之間的通信產生干擾,如圖1所示。

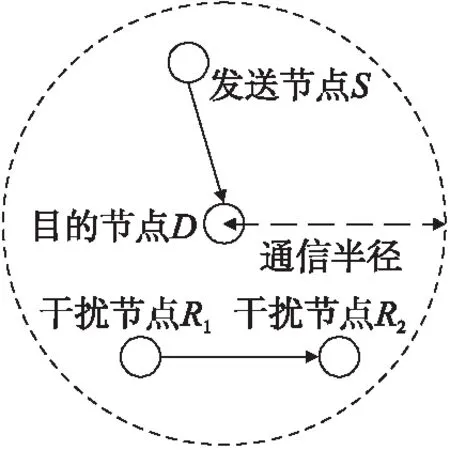
圖1 網絡傳輸干擾說明圖

以hij表示從發送節點i向目的節點j發送信息時的信道增益,計算方法表示如下[11]:

(6)

式中:dij表示發送節點i與目的節點j之間的距離,α表示介質吸收系數,ρ2表示信道衰弱系數,A表示由于多徑傳輸等因素引起的傳輸損耗。文獻[12-13]指出在深水環境中多徑衰落對水聲信道的影響較小,可以忽略不計。因此,可以取A=0,ρ2=1。信道增益公式可以簡化如下:

(7)

當發送節點i與目的節點j之間的信道信噪比SINRij滿足如下條件時,兩傳感器節點間可以正常通信。信噪比計算公式如下:

(8)

式中:ri表示發送節點i的天線方向,ri∈[0,1],Pi表示發送節點i的信息發送功率,l表示干擾節點的標號,rlPlhljtlj表示目的節點通信范圍內的干擾節點所產生的干擾功率,tlj的含義如式(1)所述,η表示信道噪聲功率,β表示信道信噪比閾值。

2 基于信噪比的虛擬力模型

2.1 虛擬力的基本思想

假設UWSN每個節點都可以感知其通信范圍內鄰居節點的相關信息。虛擬力的基本思想可以歸納為:每個節點都將受到鄰居節點的影響,這種影響以“力”的方式改變節點的移動方向以及速率。本節主要討論與覆蓋率指標相關的“節點度虛擬力”和與吞吐量指標相關的“信噪比虛擬力”設置方式。

UWSN節點分布不能過于密集,否則將造成網絡覆蓋率指標下降。為此,需要為每個節點配置節點度閾值Td。當鄰居節點的節點度超過閾值時,說明該鄰居節點周圍有很多節點,本地節點將向遠離該鄰居節點的方向移動;當鄰居節點的節點度低于閾值時,本地節點將向該鄰居節點的方向移動,如圖2所示。圖中標號為1的節點通信范圍內有4個鄰居節點,可以感知此4個鄰居節點的節點度。節點2和節點3 的節點度都低于閾值Td,節點1將向靠近節點2和節點3的方向移動;節點4和節點5的節點度都超過閾值Td,節點1將向遠離節點4和節點5的方向移動。

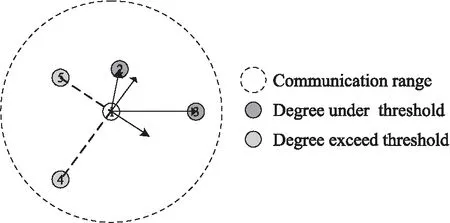
圖2 節點度閾值示意圖

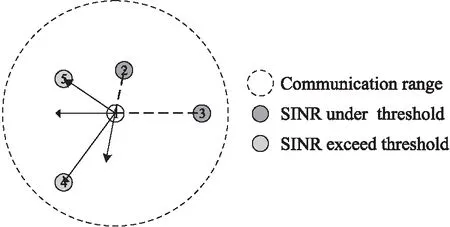
圖3 信噪比閾值示意圖

由于UWSN節點之間需要滿足鏈路信噪比閾值才能正常通信,故需要為每個節點配置信噪比閾值β。當鄰居節點與本地節點構成的鏈路信噪比超過閾值時,該節點將向鄰居節點方向移動,以增強傳輸信號強度;當鄰居節點與本地節點構成的鏈路信噪比低于閾值時,該節點將向遠離鄰居節點方向移動,如圖3所示。圖中標號為1的節點通信范圍內有4個鄰居節點,可以感知此4個鄰居節點的信噪比。節點2和節點3 的信噪比都低于閾值β,節點1將向靠近節點2和節點3的方向移動;節點4和節點5的信噪比都超過閾值β,節點1將向遠離節點4和節點5的方向移動。綜上所述,節點1的移動方式受到兩項閾值的影響。

2.2 虛擬力參數設定

節點度閾值設定是為使得節點位置均勻地分布于UWSN。因此,可以將節點位置均勻分布時,節點度的期望值作為閾值Td。在區域體積為V的UWSN中部署N個節點,節點度的期望計算方式如下二項分布公式所示:

(9)

借鑒Logistic函數[13],定義“節點度虛擬力”和“信噪比虛擬力”為取值范圍[0,1]的指數有向函數。定義時刻t鄰居節點j對本地節點i的“節點度虛擬力”αij(t)計算方式如下:

(10)

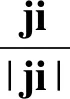
當鄰居節點的節點度小于閾值時,“節點度虛擬力”的方向與ij相同,表示向靠近鄰居節點的方向移動。此時,鄰居節點的節點度越小,虛擬力越大。當鄰居節點的節點度等于1時,“節點度虛擬力”達到最大值為1。當鄰居節點的節點度大于閾值時,“節點度虛擬力”的方向與ji相同,表示向遠離鄰居節點的方向移動。此時,鄰居節點的節點度越大,虛擬力越大。當鄰居節點的節點度等于閾值時,“節點度虛擬力”不會對本地節點的移動方式產生作用。

定義時刻t鄰居節點j對本地節點i的“信噪比虛擬力”γij(t)如下:

(11)

當本地節點與鄰居節點構成的鏈路信噪比低于閾值時,“信噪比虛擬力”的方向與ij相同,表示向靠近鄰居節點的方向移動;當本地節點與鄰居節點構成的鏈路信噪比大于閾值時,“信噪比虛擬力”的方向與ji相同,表示向遠離鄰居節點的方向移動;當本地節點與鄰居節點的鏈路信噪比等于閾值時,“信噪比虛擬力”不會對本地節點的移動方式產生作用。

在時刻t本地節點i的虛擬力ri(t)為所有鄰居節點所施加的“節點度虛擬力”和“信噪比虛擬力”之和:

(12)

時刻t本地節點i的移動方向與虛擬力ri(t)的方向一致,移動速度的計算方法如下所示:

(13)

式中:vmax表示每個節點允許移動的最大速度,vi(t)為時刻t節點i的移動速率,|ri(t)|表示時刻t節點i所受到虛擬力的數值。由于|ri(t)|是ndi個“節點度虛擬力”與ndi個“信噪比虛擬力”的合力,|ri(t)|/(2ndi)的取值范圍為[0,1]。

3 仿真分析

為評價本文所提出的算法效果,本文采用MATLAB 軟件進行數值仿真。針對一個60 m×60 m×60 m水下區域隨機散布100個傳感器節點,節點按照算法制定的移動策略進行移動。假設網絡中節點的覆蓋半徑為15 m,通信半徑為20 m,信道信噪比閾值為20 dB。假設每個節點在單位仿真時間內的最大移動速度為1 m,網絡中所有節點的初始能量為5 J。

將文獻[6]中的傳統虛擬力模型VFA、文獻[5]中的修正虛擬力模型DVFA作為本文所提出SVFA的對比算法。仿真600個單位時間,傳感器節點在每個仿真時間移動一次,網絡覆蓋率隨時間變化趨勢如圖4所示。同時,對于在網絡中部署不同數量的傳感器節點,并采用三種不同節點移動策略得到網絡最終覆蓋率如圖5所示。

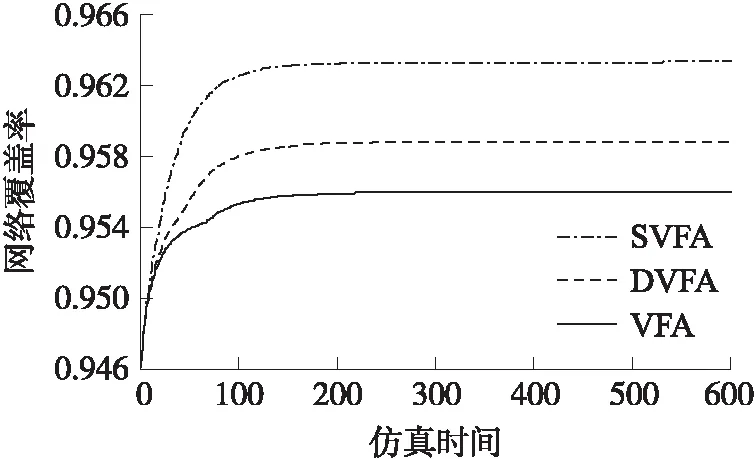
圖4 網絡覆蓋率隨仿真時間變化趨勢圖

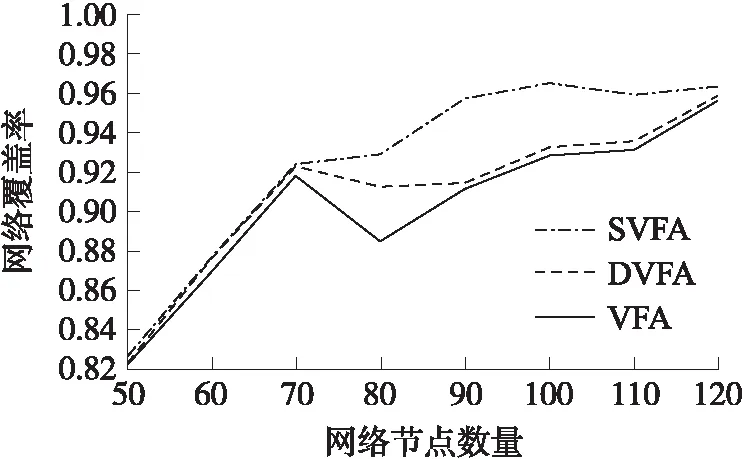
圖5 網絡覆蓋率隨節點數量變化趨勢圖

圖4顯示:在三種不同虛擬力模型所制定的節點移動策略下,隨著仿真時間推移,網絡覆蓋率快速提升,并在仿真后期逐漸趨于穩定。本文所提出的SVFA在覆蓋率上的表現優于DFVA和VFA,可以實現更高的網絡覆蓋率。此三種虛擬力模型中都考慮以節點間距離或者節點度作為關鍵指標,這些因素在一定程度上能夠保障網絡覆蓋率。圖5顯示:網絡覆蓋率隨著節點數量增加而增加,本文所提出SVFA使得網絡覆蓋率稍高于其他兩種策略獲得的網絡覆蓋率。其中,圖5中VFA曲線出現的抖動是由于隨機仿真所造成的。

當在網絡中部署100個傳感器節點時,單位時間網絡吞入量隨時間變化情況如圖6所示。定義網絡中能量最低的節點為瓶頸節點,瓶頸節點能量百分比隨仿真時間變化情況如圖7所示。

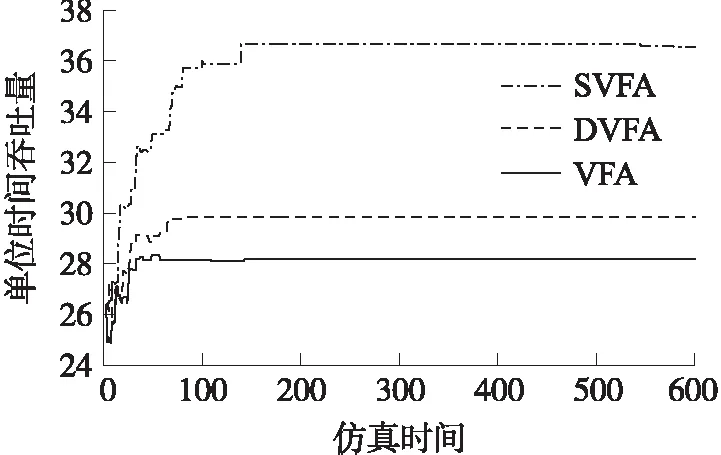
圖6 網絡吞吐量隨仿真時間變化趨勢圖

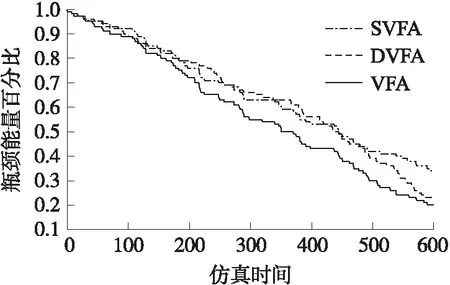
圖7 網絡瓶頸能量變化隨仿真時間變化趨勢圖

圖6顯示:在三種不同虛擬力模型所制定的節點移動策略下,隨著仿真時間推移,網絡吞吐量明顯增加。本文所提出的SVFA在覆蓋率上的表現明顯優于DFVA和VFA,可以獲得更高的網絡吞吐量,這是由于DFVA和VFA在構造過程中并未考慮鏈路信噪比所造成。圖7顯示:在三種不同虛擬力模型所制定的節點移動策略下,網絡瓶頸能量下降速度較為接近,本文所提出的SVFA在延緩瓶頸節點能量下降方面稍顯優秀。

4 結束語

本文提出一種基于信噪比的虛擬力算法。首先,考慮水下網絡信道傳輸特性,構建信道信噪比數學模型;然后,以信噪比和節點度雙指標修正傳統虛擬力模型,并制定節點移動策略。結果顯示:相比于傳統節點移動策略,本文所提出的移動策略可以有效提升網絡吞吐量,延長網絡生存時間。