非同步網絡中基于TOA的魯棒非視距目標自定位算法*

朱偉辰,王 剛

(寧波大學信息科學與工程學院,浙江 寧波 315211)

近年來,各種定位技術在我們的日常生活中發揮了重要作用。目標定位的應用包括導航,目標跟蹤,救援,航空航天等[1-4]。基于到達時間(Time-of-Arrival,TOA)的定位方法具有較高的定位精度,在實際環境中十分常用。本文考慮構造目標源自定位問題[5],錨節點在同一未知時間向目標源發送信號,目標源依靠接收信號測量TOA[6]。在這個問題中,目標源不向錨節點發送信號,因而節省了能量并延長了目標源的電池壽命。而且,本方法不要求目標源和錨節點之間保持時間同步[7]。

傳感器網絡中的時間同步問題對目標定位的精度有著不可忽略的影響,近些年來該問題已經得到了學界的廣泛研究[6-11]。在文獻[6]中通過目標源接收來自其他錨節點的信號,可以節省目標源的一些能量,并且目標源不需要與其他錨節點保持嚴格的時間同步。通過使用文獻[6]類似的信號收發方式并將時鐘偏差當成噪聲的一部分進行處理,文獻[7]提出一種有效的分式規劃(Fractional Programming,FP)方法用于估計目標源的位置。由文獻[8]可知,目標源存在的時鐘偏差(Clock Skew)和時鐘漂移(Clock Offset)是難以處理的參數。最近,文獻[9]通過將時鐘偏差視為隱藏變量,為異步接收器提出了一種集中的基于期望最大化的被動定位方法,提升了算法性能且可以達到克拉美羅下界。文獻[10]采用合作的方式同時完成傳感器網絡同步和目標源定位的工作,其中目標源之間的協作顯著提高了同步和定位的性能。文獻[11]提出了一種基于飛行時間(Time-of-Flight,TOF)的方法,該方法通過估計傳感器對的相關時鐘偏差用于修正TOF測量信息,并引入補償因子來消除多組傳感器對之間的相關時鐘偏差從而提高算法的性能。

除了傳感器間的時鐘同步問題,信號在傳播過程中可能被一些障礙阻擋,這種現象被稱為非視距(Non-Line-of-Sight,NLOS)信號傳播。非視距傳播導致信號TOA測量值中存在NLOS誤差。各種研究表明,NLOS誤差通常遠大于測量噪聲,這種誤差會對算法定位性能有著顯著的負面影響[12-16]。一些方法使用非視距誤差的分布或統計信息來提升定位精度[12-13]。然而,在時變的實際環境中很難獲得這種統計信息。文獻[14]提出了一個魯棒的半正定規劃(SDP)方法,無需NLOS誤差的統計信息。在文獻[15]中,兩種對非視距誤差具有魯棒性的方法被提出,即二階錐松弛(SOCR)和半正定松弛(SDR)方法。這兩種方法既不需要路徑狀態信息也不需要NLOS誤差的統計信息,它們只需要實際環境中是較易獲得的NLOS誤差的上界,并且表現出優于之前非魯棒方法的性能。通過給定信號到達參考錨節點的時間戳,文獻[16]將到達時間差(Time-Difference-Of-Arrival,TDOA)測量模型轉化為TOA測量模型,并聯合估計目標源發出信號的時間和位置,但該方法在非視距密集環境下定位效果較差。然而,上述文章中研究的定位問題是基于傳感器網絡完全同步這一條件,并且它們大多不具備目標源自定位的功能。因此,可以看出非同步傳感器網絡中存在NLOS誤差時的目標源自定位問題是一個全新的研究領域。

本文在NLOS條件下解決非同步傳感器網絡中基于TOA的目標源自定位問題,采用文獻[8]和[10]中的測量模型并加入了NLOS誤差。模型中存在影響問題求解的參數,例如錨節點開始傳輸信號的起始傳輸時間,時鐘偏差和時鐘漂移。通常,有兩種方法可以處理這些參數。一種是聯合估計這些參數和目標源位置,另一種是通過模型的轉換來消除它們。本文采用后者,通過使用其他測量值減去一個選定的參考測量值,可以消除起始傳輸時間和時鐘漂移而只剩下時鐘偏差。經此種處理后,TOA測量值被轉換成TDOA測量值。同時經理論分析,可以驗證文獻[15]中使用的NLOS誤差的上界過大,降低了定位性能。為克服該弊端,本文提出了一種新的魯棒最小二乘(Robust Least Square,RLS)方法,該方法聯合估計目標源位置和參考測量值中的NLOS誤差,與[15]一樣,同樣不需要路徑狀態信息或NLOS誤差的統計信息。這種做法將NLOS誤差的上界縮小至合理的范圍,從而提高了定位性能,然后根據所提出的RLS方法構造了一個非凸最小最大化優化問題。為了求解這個問題,首先應用了三角不等式來消除目標函數中的最大化部分,然后應用半正定松弛(Semidefinite Relaxation,SDR)技術將其松弛為半正定規劃(Semidefinite Programming,SDP)問題并進行求解。

1 系統模型

考慮使用k(k=2或3)維定位場景,假設傳感器網絡中存在N+1個錨節點和一個目標源,其中第i個錨節點和目標源的位置分別由si(i=0,1,…,N)和x表示,x和si都是k維列向量。所有錨節點在同一起始傳輸時間T0向目標源發送信號,目標源測量并記錄各個錨節點發送信號的TOA。假設錨節點之間是時間同步的(目標與錨節點之間不必保持時間同步),且錨節點和目標源之間的傳播路徑可能是NLOS的。基于上述假設,可將TOA測量模型寫為[8]:

(1)

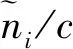
本文的目標是根據模型(1)估計未知目標源位置x,其中ω,T0和θ也是未知的。一種可能的方法是聯合估計目標源位置這些未知參數,但太多的優化變量降低了算法的性能[10]。在本文中,我們采用與文獻[7]中相同的方法:減去參考測量值并形成TDOA測量值,并通過將編號為0的錨節點指定為參考錨節點,可以將變換后的TDOA測量值表示為:

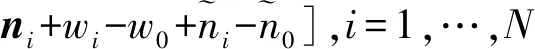
(2)

式(2)又可改寫為如下形式:

di=ω(‖x-si‖-‖x-s0‖+wi-w0+ni),i=1,…,N

(3)

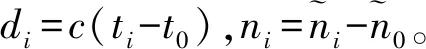
2 魯棒半正定規劃問題的推導

通常時鐘偏差ω的值約為1,故本文做出與[6]中相同的假設ω=1+δ,且采用相同的方法來處理δ,即假設δ是隨機變量并且服從區間為(-δmax,δmax)的均勻分布,其中δmax是已知常數。通常δ的值遠小于1。據此,做出以下近似1/ω=1-δ,模型(3)可近似改寫為:

di≈ri-r0+wi-w0+ni+δdi=ri-r0+wi-w0+i,i=1,…,N

(4)

式中:‖x-s0‖=r0,‖x-si‖=ri,i=ni+δdi(i=1,…,N),通過轉換δdi可以被視為測量噪聲i的一部分。

NLOS誤差會對定位性能造成非常顯著的負面影響。解決該問題的難點在于NLOS誤差的統計信息和信號傳播的路徑信息通常是未知的,這意味著不能通過將NLOS誤差與背景噪聲組合從而將式(3)轉換為視距(Line-Of-Sight,LOS)模型。文獻[15]提出了一種處理NLOS誤差方法,該方法僅需要NLOS誤差的上界。通常可假設NLOS誤差的上界為已知常數,即0≤wi≤i(i=0,…,N),并令ei=wi-w0,可以得到ei的上界為|ei|≤max{0,i}ρi,在[15]文中即對非視距誤差ei進行處理。但是,經對該種非視距誤差的結構分析,可以得出其上界過大的結論。當參考路徑上的非視距誤差w0值固定時,分析可得ei實際上落在[-w0,i-w0]的區間內,其區間長度為i。相比之下,[15]中使用的非視距誤差區間[-ρi,ρi]的長度是2ρi,明顯大于i,故導致了其算法存在額外的性能損失。由此促使本文將未知參考路徑非視距誤差w0作為變量與目標源位置進行聯合估計。

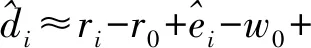
(5)

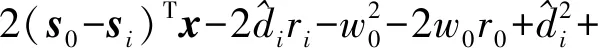
(6)

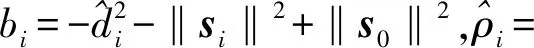
(7)

式中:ai和y是N+k+4維列向量,由此可以構造一個最壞情況下RLS問題:

s.t. ‖x-si‖=ri,i=0,…,N

(8)

為求解問題(8),本文使用三角不等式來處理式(8)中的最大化部分:

(9)

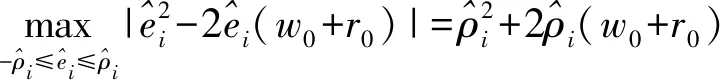
s.t. ‖x-si‖=ri,i=0,…,N

(10)

將問題(10)用上鏡圖的形式等價表述為:

i=1,…,N,

i=1,…,N,

‖x-si‖=ri,i=0,…,N

(11)

式中:η=[η1,…,ηN]T。由式(10)可以看出,問題的目標函數中只有一個絕對值符號從而會產生兩個不等式約束,所以該問題的約束數量少于[15]中問題的約束數量,但引入了更多的變量又會增加計算復雜度,具體見后文分析。問題(11)仍是非凸問題,難以求解。利用SDR技術將其放松為以下SDP問題:

(12a)

(12b)

(12c)

i=0,…,N

(12d)

式中:Y(1:k,1:k)表示矩陣Y的第1到k行和1到k列構成的子矩陣,y(1:k)表示y向量的第1到k個元素構成的子向量,而Y(k,k)和y(k)則分別代表矩陣和向量對應位置的元素。其余符號定義如下:

(13)

在文獻[15]中已經證明,添加以下二階錐約束可以改善SDP問題的精確性:

‖x-s0‖≤r0?‖x-s0‖≤y(N+k+1)‖x-si‖≤ri?‖x-si‖≤y(k+i)i=1,…,N

(14)

此外,根據已知條件0≤w0≤0并通過利用y和Y元素之間的內部關系,我們可以向問題(12)中添加如下約束:

0≤y(N+k+3)≤0y(N+k+2),0≤y(N+k+4)≤0y(N+k+1)Y(N+k+2,N+k+2)=y(N+k+3),Y(N+k+1,N+k+2)=y(N+k+4)

(15)

此外,由于NLOS誤差遠大于測量噪聲[14-15]并且δ很小的事實[6-8],使得條件|i|?wi成立,并結合式(4),可得如下不等式:

di-ri+r0+w0≥0

(16)

該結果與已知條件0≤w0≤0相結合,可以通過應用重構線性化技術(Reformulation-Linearization Technique,RLT)[17]以構成以下額外約束:

(di-ri+r0+w0)(w0-0)≤0

(di-ri+r0+w0)w0≥0

(17)

進一步,利用y和Y中對應元素重新表示約束(17)為:

diy(N+k+2)-Y(2+i,N+k+2)+y(N+k+4)+y(N+k+3)≤0(di-y(2+i)+y(N+k+1)+y(N+k+2))

(18a)

diy(N+k+2)-Y(2+i,N+k+2)+y(N+k+4)+y(N+k+3)≥0

(18b)

將約束(14),(15),(18)添加到問題(12)中,可得最終SDP問題:

(19)

至此,求解問題(19)即可得目標源的位置估計,為直觀展現算法推導遞進的過程,本節最后以圖表的形式介紹算法的具體實施步驟,內容見表1。

表1 算法流程

3 算法復雜度分析

通常混合SD/SOCP問題的復雜度可通過下式求得[15]:

(20)

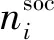
表2 算法復雜度

4 仿真結果

在本節中,通過仿真實驗對所提出方法與其他方法的定位性能進行比較驗證。各錨節點位置在表3中給出,目標源位置從[-50,50]×[-50,50]的正方形區域中隨機產生。

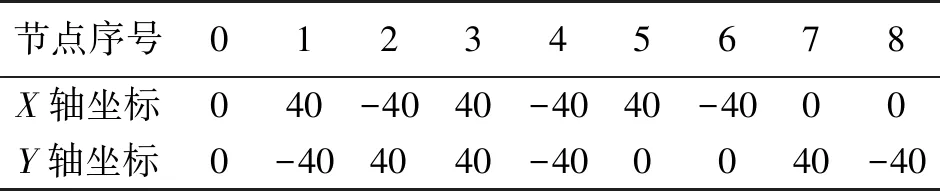
表3 錨節點位置

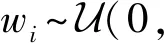
場景一:在這種場景下,固定錨節點的個數為5(N=4),同時設置0=2,i=20α(i=1,…,4)。如圖1所示,本文提出方法整體優于其他五種方法,且優勢隨α的增加愈加明顯。具體的,當α=1時,與SOCP-Robust和SDP-Robust相比,本文提出方法的RMSE降低了3.1 m。需要注意的是,當α較大時,SDP-Robust和SOCP-Robust方法中的非視距誤差ei大多符號為正,這意味著三角不等式中的等式基本不成立,嚴重影響了方法性能。隨著α的增大SDP-TOA方法的定位精度快速下降,因其需要估計與NLOS誤差相關的參數在較大NLOS誤差的情況下無法得到精確的估計值。

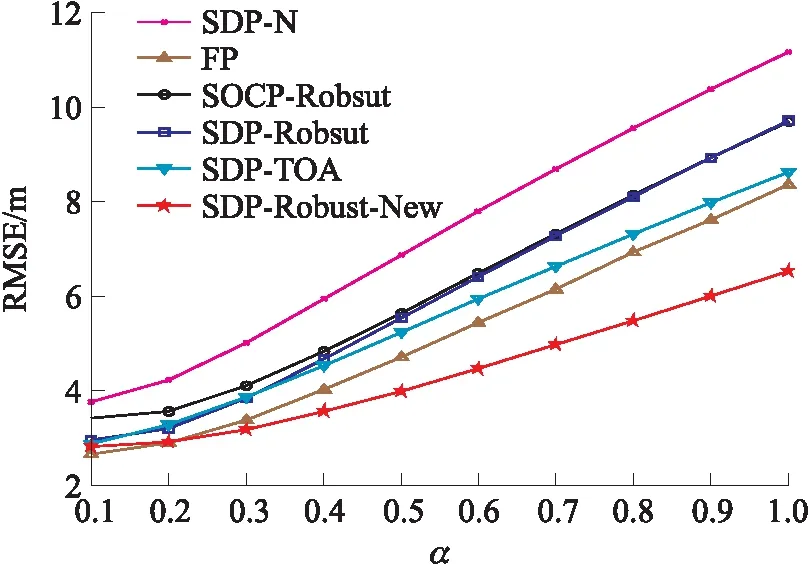
圖1 當α變化,0=2,i=20α時各方法性能對比

場景二:在這種場景下,固定錨節點的個數為5個(N=4),同時設置0=20,i=20α(i=1,…,4)。由圖2可知,參考路徑上的NLOS誤差嚴重影響了FP和SDP-N方法的定位效果。根據文獻[15]可知,SDP-Robust和SOCP-Robust方法直接受到非視距誤差ei量級的影響。該場景下,隨著α的增加非視距誤差ei量級下降但三角不等式中的等式也漸漸無法滿足,故造成了SDP-Robust和SOCP-Robust方法定位效果的波動。與其他方法不同,所提出的方法幾乎不受參考路徑上的NLOS誤差的影響。原因是本文將w0作為估計變量同時用魯棒方法處理NLOS誤差。因此,所提出的方法僅受到wi量級大小的影響,仿真結果已經清楚地說明了這一點。同樣受到非視距誤差wi影響的SDP-TOA方法的定位效果則下降較快,最后在α=1甚的時候甚至比不過SDP-Robust方法,也印證了文獻[16]中的結果。

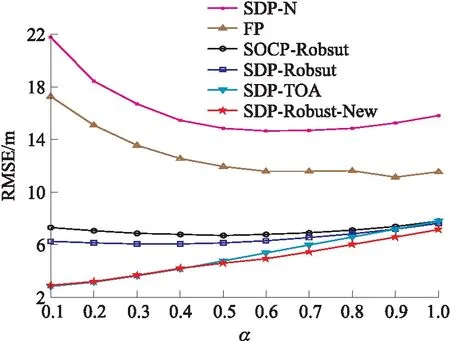
圖2 當α變化,0=20,i=20α時各方法性能對比

場景三:在這種場景下,錨節點個數由5增加到9,即N由4增加到8,時設置0=i=20(i=1,…,N)。如圖3所示,因為未對非視距誤差做出有效處理,在非視距誤差較大的環境下FP和SDP-N表現較差。本文提出的方法定位性能隨錨節點個數增加而逐漸提升,且仍在定位效果上具有優勢。尤其是與SDP-N方法相比,本文方法具有超過6 m的RMSE降低。SDP-Robust和SOCP-Robust方法表現出異常的仿真結果,即隨著錨節點個數的增加,性能可能無法穩定提升。此現象可歸因于這樣的事實:隨著錨節點個數的增加,不合適的非視距誤差上界問題將對更多測量值產生負面影響。

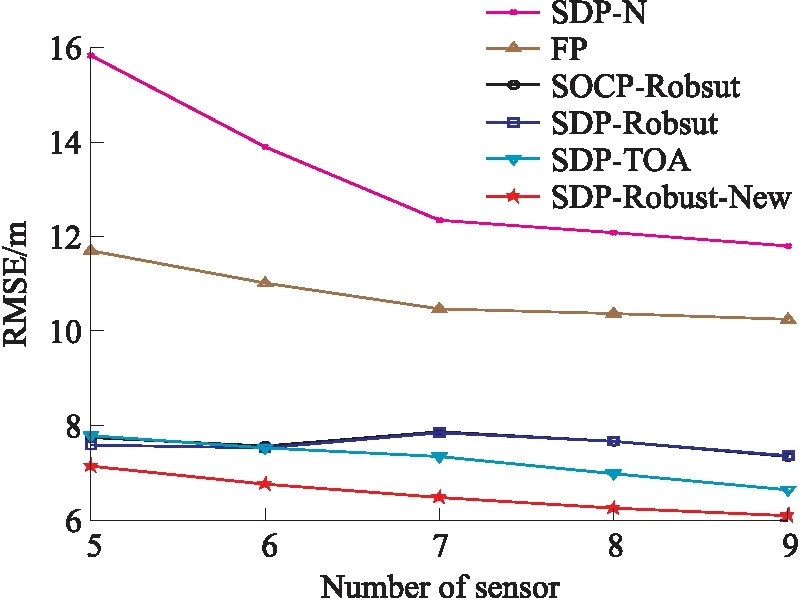
圖3 當錨節點數量N變化時各方法性能對比

5 總結

本文提出了一種新的RLS方法,在非同步網絡中對NLOS條件下基于TOA的目標源自定位問題的求解有較好的效果。所提出的RLS方法通過模型轉換消去了原模型中存在的一些干擾參數,解決了現有其他方法中存在的不合適的非視距誤差上界問題,并挖掘出各優化變量間存在的關系,將這些關系轉化為合理的凸約束,因此改善了定位性能。仿真結果證實了該方法的良好性能,并展現了方法對減輕NLOS誤差影響的顯著效果。