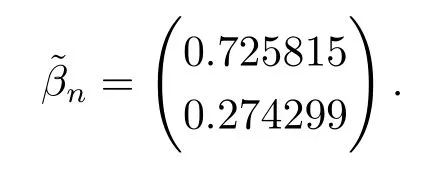長(zhǎng)相依固定設(shè)計(jì)下部分線性EV 模型的小波估計(jì)的漸近性質(zhì)
劉香, 胡宏昌, 余新新
(湖北師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)學(xué)院, 湖北黃石435001)
1 引言
部分線性EV 模型如下

這里{yk,k=1,2,···,n} 是觀測(cè)值,β是一維未知參數(shù),g(t) 是光滑的曲線, {tk} 為區(qū)間[0,1]內(nèi)的序列.{εk,k=1,2,···,n} 表示隨機(jī)誤差, 變量{xk} 不能直接被觀測(cè), 只能通過Xk=xk+uk來觀測(cè), 其中{uk} 是測(cè)量誤差, 且假設(shè){uk} 為已知獨(dú)立同分布的隨機(jī)變量, 而且對(duì)于每個(gè)k值, {uk} 與{εk,k=1,2,···,n} 都是相互獨(dú)立的.假設(shè)E(εi)=0, var(εi)=1 (即假定已知).則自協(xié)方差函數(shù)為

這里0<θ<1 是常數(shù),L(t),t∈(0,∞) 是正的緩慢變化函數(shù), 即
幾十年來, 部分線性EV 模型已經(jīng)被廣泛研究, 文獻(xiàn)[1–4]用小波估計(jì)的方法研究了部分線性回歸模型, 在誤差序列{εk} 獨(dú)立同分布時(shí), 得到估計(jì)量的大樣本性質(zhì); 若其誤差為鞅差序列, 如參考文獻(xiàn)[5], 則使用近鄰估計(jì)方法來研究了部分線性EV 模型.相依誤差的一個(gè)重要的特殊情況就是誤差為長(zhǎng)相依的.這種情況會(huì)出現(xiàn)在經(jīng)濟(jì)學(xué), 時(shí)間序列分析和其他學(xué)科領(lǐng)域的運(yùn)用中, 見文獻(xiàn)[6–8].使用小波估計(jì)對(duì)半?yún)?shù)模型的研究見文獻(xiàn)[3, 9].文獻(xiàn)[10]是對(duì)固定設(shè)計(jì)下的半?yún)?shù)回歸模型使用非參數(shù)權(quán)函數(shù)法和最小二乘法.在一定的正則性條件下, 文獻(xiàn)[11]中研究了部分線性模型中參數(shù)β和函數(shù)g(·) 的估計(jì)的弱相合性, 均方相合性和收斂速度, 得到了這些估計(jì)的漸近表示和漸近分布; 文獻(xiàn)[12]研究了長(zhǎng)相依隨機(jī)設(shè)計(jì)下的部分線性EV 模型, 得到了參數(shù)估計(jì)量的漸近表示, 漸近分布和弱收斂速度.本文是在這些文獻(xiàn)的基礎(chǔ)上, 運(yùn)用小波估計(jì)研究了固定設(shè)計(jì)下的參數(shù)估計(jì)量的漸近表示, 漸近分布和弱收斂速度.
2 小波估計(jì)
本節(jié)中, 我們使用小波方法估計(jì)未知參數(shù)和非參數(shù).令A(yù)i=[si?1,si]表示區(qū)間[0,1]的劃分區(qū)間, 且由(1.1) 式, 得到

假設(shè)Schwartz 空間Sl中存在尺度函數(shù)φ(x), 在伴隨Hilbert 空間中存在多分辨率分析Vm,它的再生核定義為將(2.3) 式看成一般部分線性回歸模型.首先, 假設(shè)β已知, 定義g(t) 的估計(jì)量為

然后, 通過最小化方法來定義小波估計(jì)量
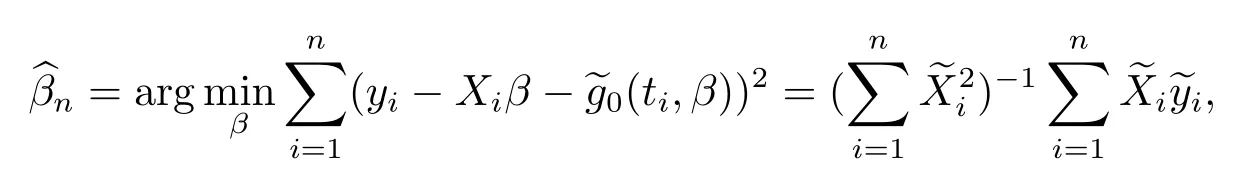
由于在線性回歸或在部分線性回歸中, 由測(cè)量誤差所導(dǎo)致的不一致性可由“衰減效應(yīng)”所克服.因此使用以下修正的最小二乘估計(jì)量

最后, 定義g(t) 的小波估計(jì)量為

3 主要結(jié)果
為了獲得主要結(jié)果, 作如下假設(shè)條件
(1) 令xj=f(tj)+νj,j=1,2,···,n, 這里f(tj) 是區(qū)間[0,1]中的函數(shù), 對(duì)于實(shí)數(shù)列{νi}, 有
(2)g(·),f(·)∈Hα(Sobolev 空間),α>1/2;
(3)g(·),f(·) 都是階數(shù)為γ>0 的Lipschitz 函數(shù);
(4) 2m=O(n?1),0<θ 注1條件(2)–(4) 在小波估計(jì)中常被用到(見文獻(xiàn)[4,10,17,19]).條件(1) 是研究部分線性模型時(shí)常用到的條件, 但是本文條件與他們有所不同. (1)文獻(xiàn)[9,10,13]均對(duì)|νi|p(p≥2) 施加條件, 本文僅對(duì)|νi| 施加條件; (2)文獻(xiàn)[9,10,13]中對(duì)νi施加的條件較多, 本文對(duì)νi僅有一個(gè)條件; (3)雖然文獻(xiàn)[10,13]的條件及文獻(xiàn)[9]中的條件A1)i) 均可由本文中νi的條件(條件(1)) 推出(本文中νi的條件比文獻(xiàn)[10,13]的條件及文獻(xiàn)[9]中的條件1 強(qiáng)), 但本文中νi的條件推不出文獻(xiàn)[9]中的條件A1)ii).說明本文νi條件比文獻(xiàn)[9]中的條件A1) ii) 弱. 因此文獻(xiàn)[9]中條件A1)ii) 不成立. 注2與文獻(xiàn)[12]類似, 文獻(xiàn)[12]是隨機(jī)變量, 本文是固定設(shè)計(jì). 定理1假設(shè)條件(1)–(4) 均成立, 則對(duì)任意的α≥3/2, 且有 假設(shè)定理1 的條件及結(jié)論成立, 則有以下推論, 其中推論1 和推論2 與文獻(xiàn)[12]中推論相同. 推論1若{ek,k=1,2,· · ·} 是獨(dú)立隨機(jī)變量,G(s)=s, 則對(duì)E|uk|4+2δ< ∞,有 推論2在定理1 的條件下, 若uk=0, 則 定理2若定理1 的條件成立, 則對(duì)λ/<θ, 且有 為了證明主要結(jié)果, 首先介紹一些有用的結(jié)論及引理. 首先介紹Hermite 秩的表示和Hermite 級(jí)數(shù)的一些基本結(jié)論.令e表示N(0,1) 上的隨機(jī)變量, 且G={G:E(G(e))=0,E(G2(e))<∞}, 則G是 構(gòu)成了L2(R,Φ(s)) 中函數(shù)的完整正交系統(tǒng), 并滿足E(Hl(e)Hq(e))=δlqq!. 對(duì)任意的G∈G, 令J(q)=EG(e)Hq(e).定義且為G的Hermite 秩.由于J(0)=E(G)=0, 故通常是正數(shù). 令{ek,k=1,2,···,n} 和ρ(k) 如上所述,>0 為固定常數(shù), 則以下結(jié)果成立[18]. (F2) 對(duì)任意Hermite 秩為<1/θ, 可測(cè)函數(shù)G∈L2(R,Φ(s)), 特別的, (F3) 對(duì)任意緩慢變化函數(shù)L(n) 而言, 有 (F4) {Hq(ei)} 是L2(R,Φ(s)) 中的一列隨機(jī)變量, 且滿足 引理1[3]假設(shè)條件(3) 成立, 則 引理2假設(shè)條件(1) 和(3) 成立, 則xi有界,有界, 且 證由于{νi} 是實(shí)數(shù)列,f(·) 是階數(shù)為γ> 0 的Lipschitz 函數(shù), 故xj=f(tj)+νj,j=1,2,··· ,n有界.由和引理1(2), 有 引理3令則有 證為了證明此引理, 只需證明注意到 由Cr不等式及引理2, 有 由ui的獨(dú)立性得 由引理1 及ui的獨(dú)立性得 引理4[14]假設(shè)條件(1)–(4) 成立, 則 引理5[11]假設(shè)條件(4) 成立, 則對(duì)每個(gè)實(shí)數(shù)a1,a2,···,an, 下列分解成立 這里Tl1,Tl2滿足 引理6[13]令表示函數(shù)G∈G 的Hermite 秩,ai表示有界的非負(fù)實(shí)數(shù), 則它的Hermite 秩也是, 且 引理7[15]若G(ei)∈G 的Hermite 秩是, 則 定理1 的證明對(duì)由引理2 進(jìn)行如下分解 由引理6 及(F4) 有 由引理2 及(F4) 有 對(duì)Tn3求二階矩 由引理2 及(F2) 有 由引理6 及(F2) 有 由(5.3)–(5.4) 式可得 對(duì)Tn4求二階矩 由引理2 及(F2) 有 由引理6 及(F2) 有 由(5.6)–(5.7) 式可得 對(duì)Tn5求二階矩 由引理2 有 由引理2 及引理6 有 由(5.9)–(5.10) 式可得 由(F4) 有 對(duì)Tn7求二階矩 由(F2) 有 由(5.12) 式及(F2) 有 由(5.14)–(5.15) 式可得 對(duì)Tn8求二階矩 由(F2) 有 由(5.12) 式及(F2) 有 由(5.17)–(5.18) 式可得 對(duì)Tn9求二階矩 由引理2 有 由(5.12) 式及引理2 有 由(5.20)–(5.21) 式可得 對(duì)Tn10求二階矩 由(5.12) 式, 有 由(5.23)–(5.24) 式可得 由(5.12) 和Chebyshev 不等式可得 定理1 證畢. 推論1 的證明由(3.1) 和(5.28) 式, 有 因此由(5.29)–(5.30) 式得推論1 成立. 推論2 的證明由(3.1) 和(5.28) 式, 有 因?yàn)?/p> 且 因此由(5.31)–(5.32) 式得推論2 成立. 定理2 的證明 注意到 因?yàn)?/p> 所以有 從而 由上式和引理2 有 由引理6 和引理7 有 由引理1 有 因此由Markov 不等式和(F3) 可得 由引理1, 可得到 定理2 證畢. 為了對(duì)本文的證明結(jié)果做進(jìn)一步的解釋和驗(yàn)證, 選取2013 年5 月到2018 年8 月之間的全國(guó)居民消費(fèi)價(jià)格指數(shù), 城市居民消費(fèi)價(jià)格指數(shù)和農(nóng)村居民消費(fèi)價(jià)格指數(shù), 使用Mathmatic來做模擬應(yīng)用(具體數(shù)值見東方財(cái)富網(wǎng)《中國(guó)居民消費(fèi)價(jià)格指數(shù)》). 使用下述的式子 其中設(shè)全國(guó)居民消費(fèi)價(jià)格指數(shù)為y, 城市居民消費(fèi)價(jià)格指數(shù)和農(nóng)村居民消費(fèi)價(jià)格指數(shù)為矩陣X, 通過X, 由Mathmatic 算得 圖1: (t) 的散點(diǎn)圖 相對(duì)誤差H由下式算得 64 個(gè)數(shù)據(jù)中有55 個(gè)在0.05%以內(nèi),占總數(shù)的85.94%;有9 個(gè)在0.1%以內(nèi),占總數(shù)的14.06%,在一定程度上說明估計(jì)出的和(t) 是有效的.這個(gè)例子也直接說明了本文前面所證明的結(jié)論是正確的, 對(duì)于數(shù)據(jù)處理預(yù)測(cè)也有實(shí)際的作用. 具體計(jì)算的結(jié)果如下表1. 表1: 相對(duì)誤差表

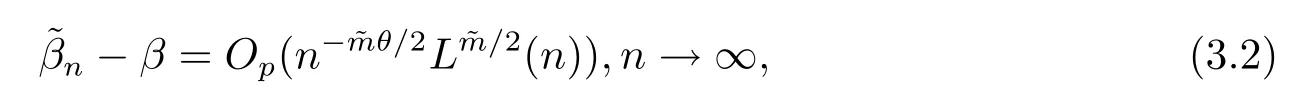
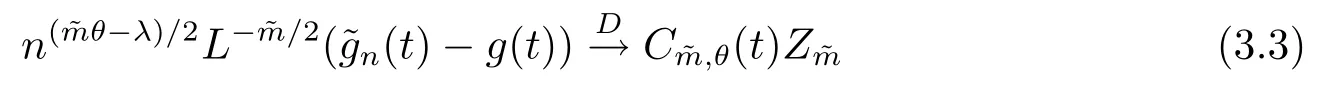

4 主要結(jié)果證明所需的引理



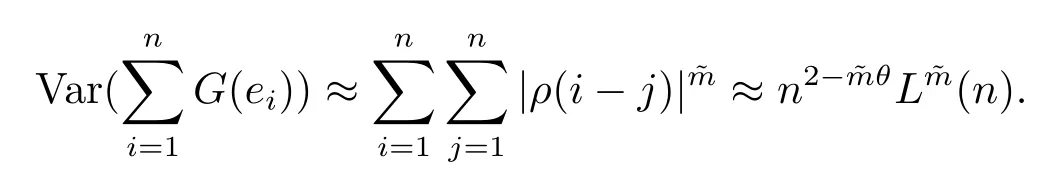




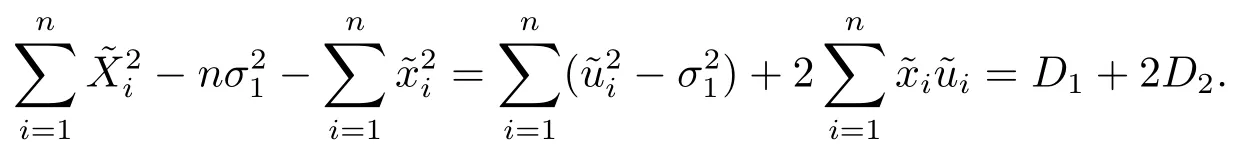
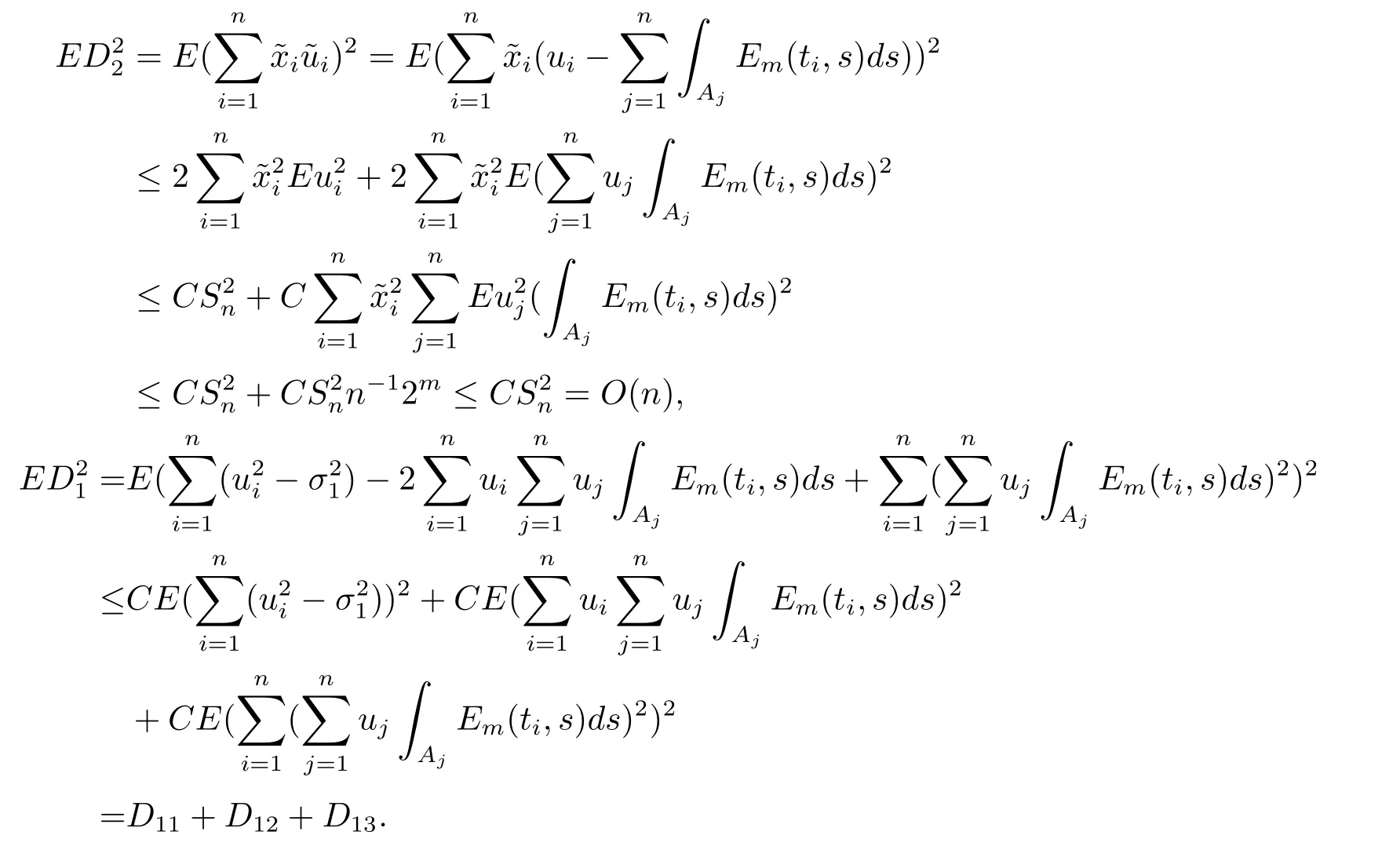




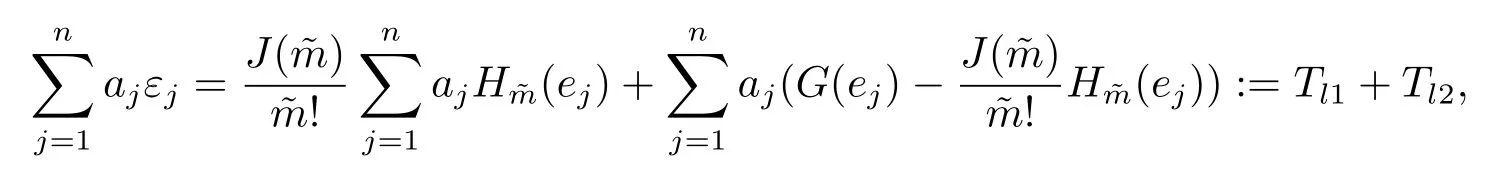
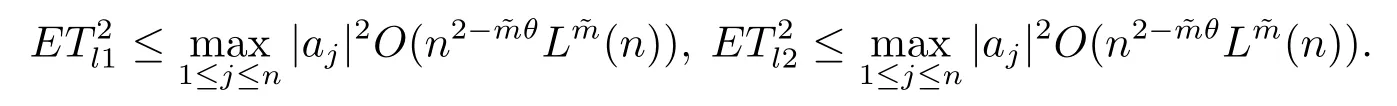


5 主要結(jié)果的證明




















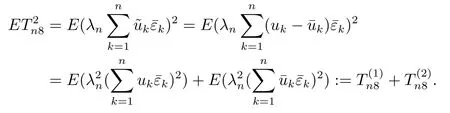

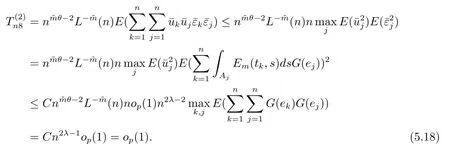






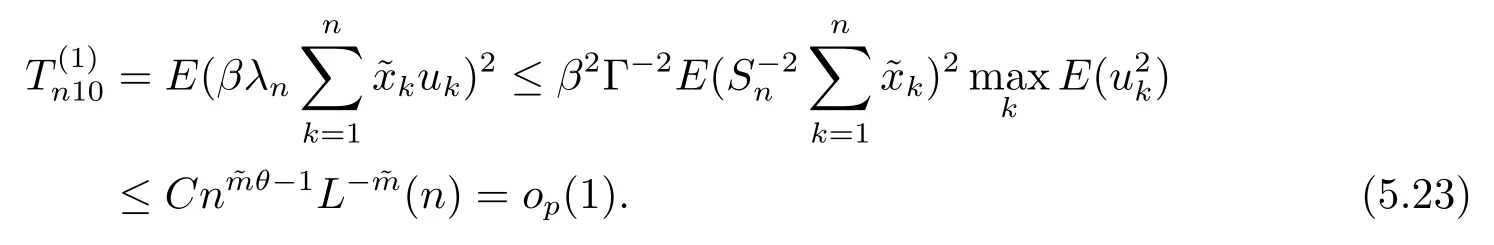
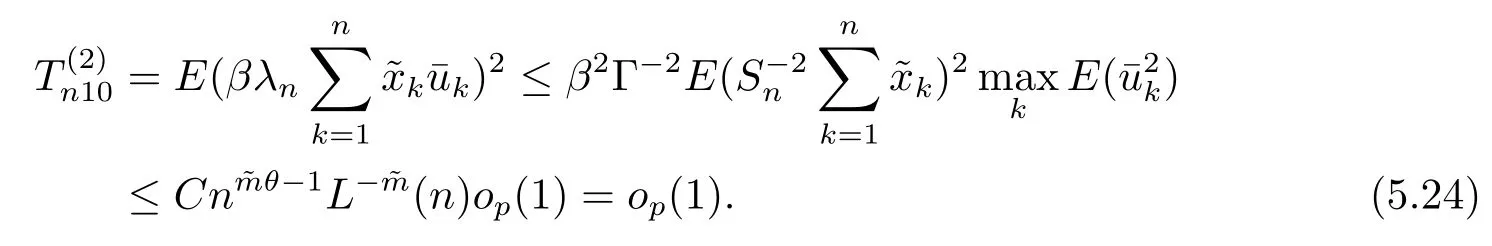






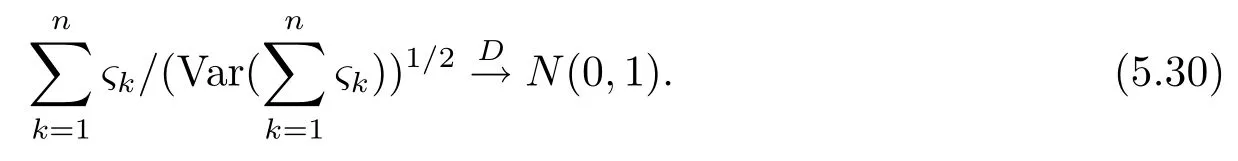








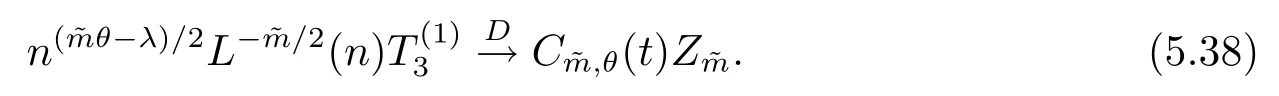


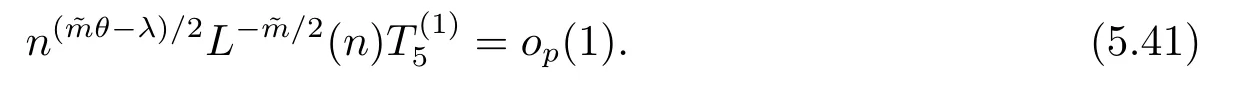
6 模擬例子