基于試驗數(shù)據(jù)統(tǒng)計的畸變特性關聯(lián)模型

吳森林，葉 巍，張 毅，劉曉晨，王迎國

(中國航發(fā)四川燃氣渦輪研究院，四川綿陽 621010)

1 引言

發(fā)動機氣動穩(wěn)定性評定是進氣道與發(fā)動機相容性評定中最核心的內(nèi)容，規(guī)范發(fā)動機穩(wěn)定性設計與評定是發(fā)動機研制過程中不可回避的關鍵問題。針對該關鍵問題，國內(nèi)外航空技術人員開展了大量進氣畸變對發(fā)動機氣動穩(wěn)定性影響的研究，并建立了具體的評定方法和標準，如SAE ARP-1420、SAE AIR-1429、GJB/Z64 等。但由于所使用的理論分析方法還不夠完善，迄今為止主要還是依靠試驗驗證手段來完成對發(fā)動機氣動穩(wěn)定性的評定。而壓氣機作為航空發(fā)動機的核心部件之一，其氣動穩(wěn)定性直接關系到發(fā)動機的工作狀態(tài)，因此，在航空發(fā)動機研制過程中，壓氣機的氣動穩(wěn)定性評定被定為必不可少的試驗科目之一。目前國外采用的發(fā)動機壓氣機穩(wěn)定性評定試驗方法，主要有英、美等國采用的模擬板和模擬網(wǎng)試驗方法[1-2]，以及俄羅斯采用的固定式插板試驗方法[3-5]。

采用固定式插板方法進行發(fā)動機壓氣機氣動穩(wěn)定性檢驗，可以在壓氣機進口產(chǎn)生穩(wěn)態(tài)壓力畸變流場以及表現(xiàn)為頻率和振幅隨機變化的“紊流”畸變流場。這兩種畸變共同影響壓氣機工作的穩(wěn)定性。當綜合畸變指數(shù)達到一定數(shù)值(一般為3%～10%)時，才能有效地評定壓氣機的抗畸變能力。不同壓氣機的進口氣流速度不同，其固定式插板的深度和安裝位置就不同。為了達到一定的畸變指數(shù)，在制定畸變試驗方案時，一般需要加工4 組插入深度的插板和3 組安裝距離的進氣道，試驗過程也需試著安裝2～4 組插板和2～3 組安裝距離[6-8]，并進行多次試驗。這樣既提高了試驗成本，又增加了試驗風險。對試驗數(shù)據(jù)進行統(tǒng)計后發(fā)現(xiàn)，在某一固定插板深度下，畸變指數(shù)隨進口氣流馬赫數(shù)呈單值遞增函數(shù)變化[9-11]。本文利用這一規(guī)律，對單位已有的壓縮部件試驗數(shù)據(jù)進行了整理分析，獲取了不完全統(tǒng)計規(guī)律下的關聯(lián)模型，并將該模型成功應用于壓縮部件進氣畸變試驗方案制定中，可降低試驗成本、提高試驗效率。

2 試驗數(shù)據(jù)統(tǒng)計及處理

2.1 數(shù)據(jù)統(tǒng)計

共收集整理了6 臺份風扇/壓氣機畸變試驗數(shù)據(jù)，表1 給出了各臺份在設計點附近的進口馬赫數(shù)(Ma)和進氣道直徑(D)。可以看出，壓氣機設計點的流速在0.13～0.50 馬赫范圍，進氣道直徑在200～850 mm 之間，包含了當前大多數(shù)風扇/壓氣機的進氣流速范圍，基本可以表征風扇/壓氣機進氣畸變的強度特性。

2.2 數(shù)據(jù)處理

(1) 綜合畸變指數(shù)相對偏差

綜合畸變指數(shù)相對偏差為本文建立的關聯(lián)模型與試驗獲取的綜合畸變指數(shù)之間的偏差大小，表征了關聯(lián)模型對畸變指數(shù)預測的準確性。

式中：ΔWx為綜合畸變指數(shù)相對偏差，Wj為采用關聯(lián)模型計算得到的綜合畸變指數(shù)，W為試驗中獲取的綜合畸變指數(shù)。

(2) 進口馬赫數(shù)

為將不同狀態(tài)畸變特性統(tǒng)一到一個基準上進行對比分析，本文定義了進口馬赫數(shù)Ma(為插板前未受到擾動的均勻氣流速度，即插板前來流馬赫數(shù))。可通過公式(2)計算得到流量函數(shù)q(λ)，再查表得到Ma。

式中：G為流量管上測取的進口物理流量，T*為穩(wěn)壓箱內(nèi)測取的進氣總溫，p*為穩(wěn)壓箱內(nèi)測取的進氣總壓，A為進氣道面積。

2.3 統(tǒng)計原則

分別整理統(tǒng)計了5 組插板深度(H)下，5 組氣動界面與插板距離(L，下面簡稱安裝距離)的畸變數(shù)據(jù)，如表2 所示。

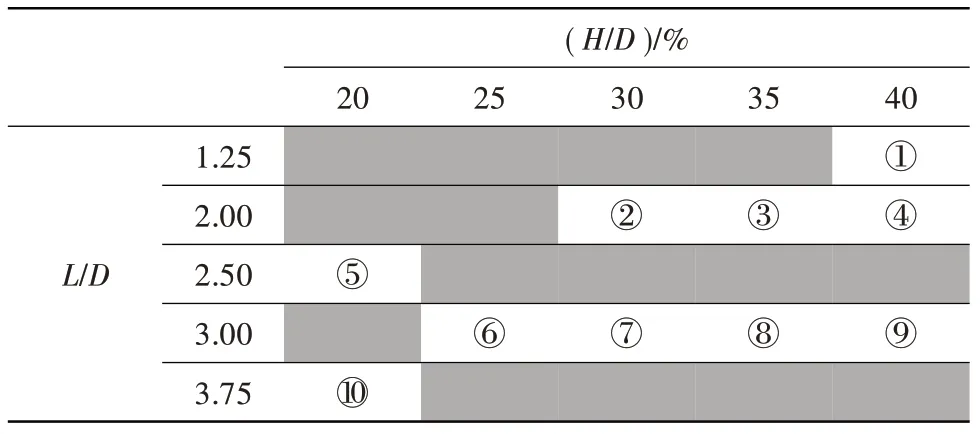
表2 畸變發(fā)生器的布置狀態(tài)Table 2 Position conditions of distortion generators

基于數(shù)據(jù)量限制，為使擬合曲線的馬赫數(shù)范圍更大，將L=2.95D、3.11D的數(shù)據(jù)近似為3.00D(前期的數(shù)據(jù)統(tǒng)計發(fā)現(xiàn)，L=2.95D、3.11D與L=3.00D的周向畸變指數(shù)變化均在測試誤差范圍內(nèi))，將L=2.06D、2.20D的數(shù)據(jù)近似為2.00D。數(shù)據(jù)擬合過程中，考慮到馬赫數(shù)等于零時流場不存在畸變，此時畸變指數(shù)理論上應為零，因此曲線擬合時采用過零點擬合。

3 數(shù)據(jù)分析

3.1 進氣道直徑對畸變特性的影響

在上述所統(tǒng)計的試驗數(shù)據(jù)中，進氣道直徑從200 mm 到850 mm 不等，為明確進氣道直徑對畸變特性的影響程度，本文對不同進氣道直徑(750 mm和801 mm)下的插板吹風試驗數(shù)據(jù)進行了對比。從圖1 可以看出，在插板深度相同時，不同進氣道直徑之間的總壓恢復系數(shù)和周向畸變指數(shù)隨馬赫數(shù)的變化曲線重合性均相當好，總壓恢復系數(shù)最大偏差約為1.0%，周向畸變指數(shù)最大偏差約為0.2%，均在測試誤差范圍內(nèi)。據(jù)此可認為，進氣道直徑對畸變特性的影響可忽略，后續(xù)統(tǒng)計規(guī)律中不再考慮進氣道直徑的影響。

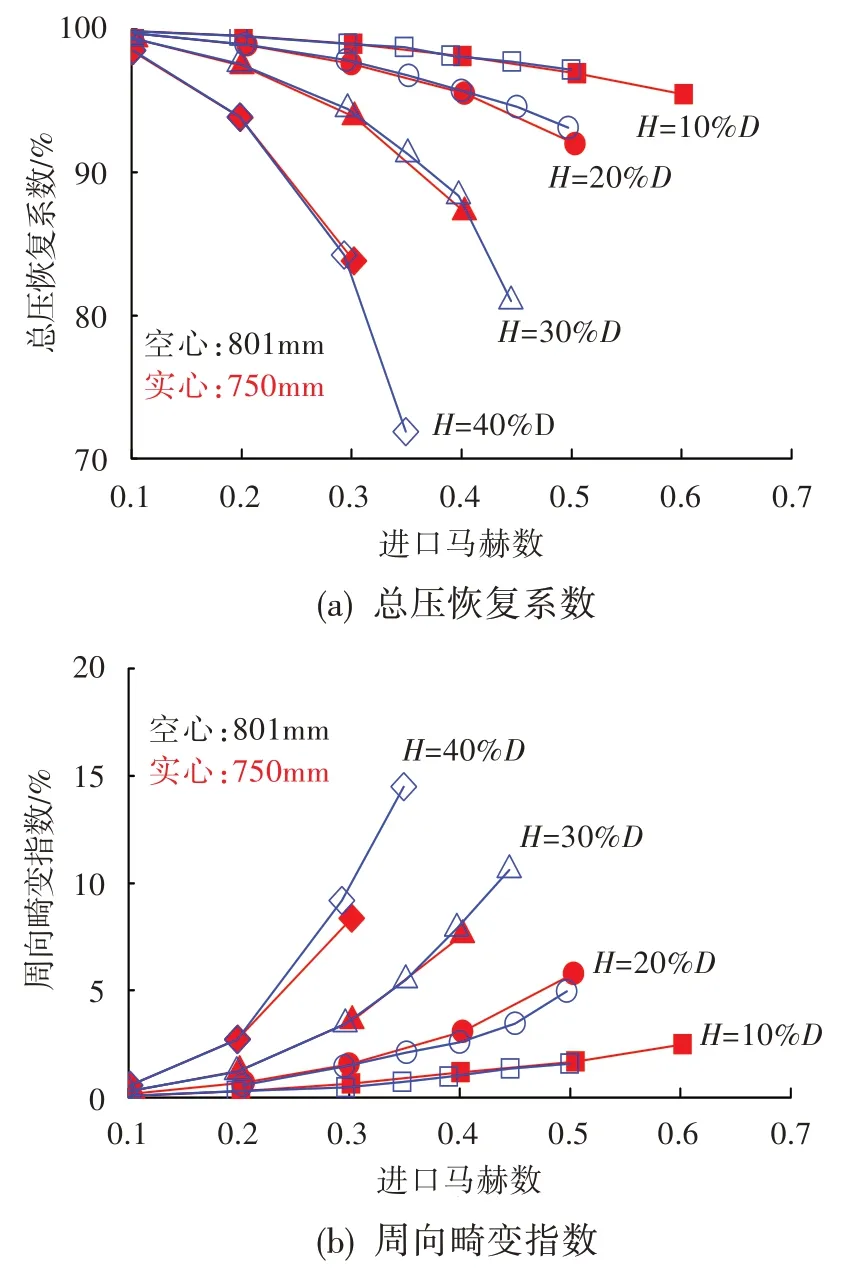
圖1 不同進氣道直徑下的畸變流場特性對比Fig.1 Comparison of distortion flow field at different flow channel diameters

3.2 畸變指數(shù)關聯(lián)模型

3.2.1 模型的建立

通過對上述6 臺份壓氣機10 種畸變發(fā)生器布局方案試驗數(shù)據(jù)進行整理分析，將各狀態(tài)的綜合畸變指數(shù)隨馬赫數(shù)變化的離散點進行對比(圖2)可以發(fā)現(xiàn)，同一種畸變發(fā)生器布局方案下，綜合畸變指數(shù)隨馬赫數(shù)的線性分布趨勢非常好。根據(jù)離散點的分布規(guī)律，分別采用了2、3、4、5、6 階次進行多項式擬合，發(fā)現(xiàn)當擬合階次高于4 次方后容易導致低馬赫數(shù)下畸變指數(shù)為負值，因此本文采用3 次方進行擬合。圖3 給出了各狀態(tài)下綜合畸變指數(shù)隨馬赫數(shù)的關聯(lián)模型。圖中，虛線為通過關聯(lián)模型外插部分，實線為試驗數(shù)據(jù)擬合部分。

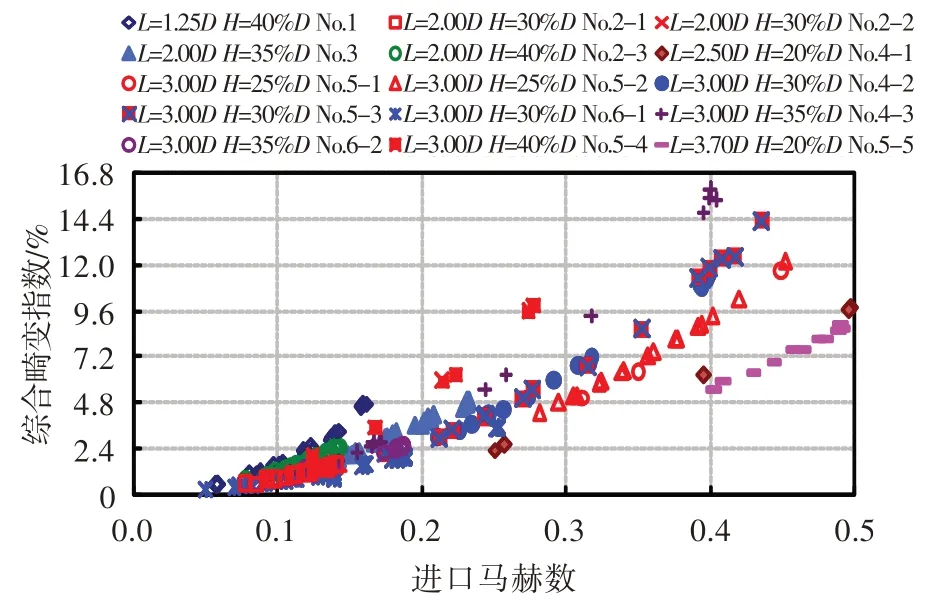
圖2 綜合畸變指數(shù)隨進口馬赫數(shù)的離散點Fig.2 The discrete points of comprehensive distortion index along with inlet Mach number

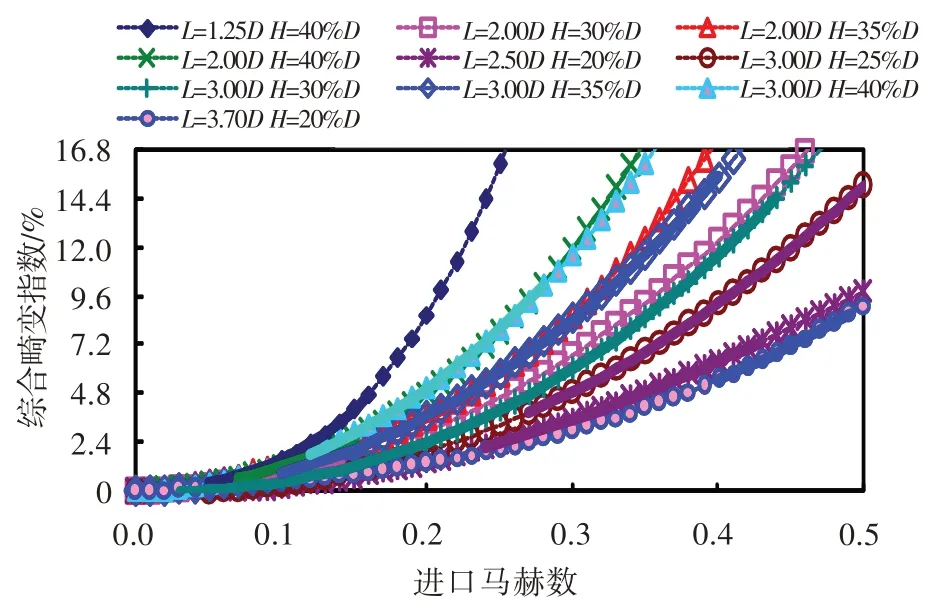
圖3 綜合畸變指數(shù)隨進口馬赫數(shù)的關聯(lián)特性Fig.3 Correlation characteristics of comprehensive distortion index along with inlet Mach number

結合圖3 和表2 可以看出，狀態(tài)②與⑦、③與⑧、④與⑨、⑤與⑩的關聯(lián)模型差異較小，狀態(tài)①與其相同插板深度的關聯(lián)模型差異明顯。但整體上講，同一插板深度下不同安裝距離的綜合畸變指數(shù)差異較小，而同一安裝距離下不同插板深度的綜合畸變指數(shù)差異較大。這說明，相比于安裝距離，調(diào)整插板深度更容易改變進氣畸變流場。

圖4 綜合畸變指數(shù)關聯(lián)模型預測偏差Fig.4 Relative deviation caused by correlation model of comprehensive distortion index

為驗證圖3 中各關聯(lián)模型對綜合畸變指數(shù)預測的準確性，圖4 給出了全部壓氣機性能試驗獲取的綜合畸變指數(shù)與相對應的關聯(lián)模型之間的偏差統(tǒng)計。可以發(fā)現(xiàn)，在0.2 馬赫數(shù)以下有少部分離散點相對偏差超過了25.0%，整個馬赫數(shù)范圍絕大部分離散點的相對偏差處于14.0%范圍內(nèi)。從圖5 也可以看出，相對偏差大于14.0%的離散點數(shù)目只占所有統(tǒng)計離散點總數(shù)的13.7%。由此可說明，本文建立的關聯(lián)模型，在所擬合的馬赫數(shù)范圍內(nèi)可以用于指導壓縮部件進氣畸變試驗插板布局方案的制定，但在擬合的馬赫數(shù)范圍外仍需要進一步驗證。

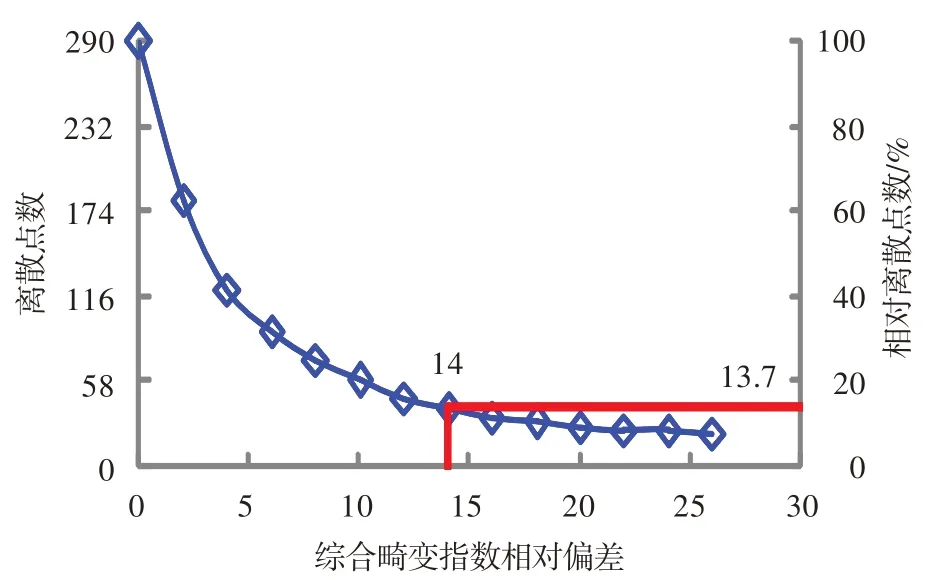
圖5 預測偏差與離散點數(shù)目的關系Fig.5 Relation of predicted deviation and the number of discrete points

3.2.2 模型的工程應用

在多臺份壓縮部件進氣畸變試驗方案制定中對關聯(lián)模型進行了應用驗證。從圖6 中關聯(lián)模型應用前后試驗效率的對比結果可以看出，模型建立前，插板深度需要使用2～4 組，插板安裝距離分別要使用2～3 組，需要3～6 次試驗才能完成預定試驗內(nèi)容；應用模型后，只需要1 組插板和1 組安裝距離，開展1～2 次試驗即可完成預定試驗內(nèi)容，試驗效率提升了1 倍。另外，在某風扇畸變試驗中，應用關聯(lián)模型所預測的綜合畸變指數(shù)與實測值的相對偏差不到10.0%，也進一步驗證了模型的準確性。

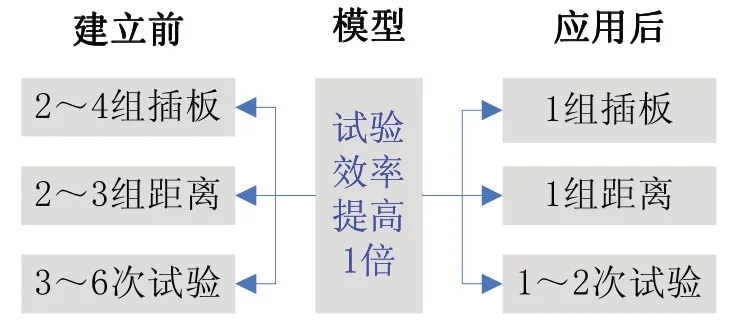
圖6 模型應用前后試驗效率對比Fig.6 Comparison of test efficiency before and after model application

3.3 穩(wěn)動態(tài)畸變指數(shù)占比統(tǒng)計

在壓氣機進氣畸變試驗中，用于評定壓氣機抗畸變能力的參數(shù)有綜合畸變指數(shù)和穩(wěn)定裕度損失，其中綜合畸變指數(shù)為周向畸變指數(shù)與紊流度之和。由于紊流度屬于動態(tài)參數(shù)，受白噪聲、濾波結構形式、采樣頻率、采樣周期等因素影響，其測試誤差一般較大。為了在數(shù)據(jù)處理過程中判斷紊流度的有效性，圖7 給出了周向畸變指數(shù)在綜合畸變指數(shù)中所占的百分比統(tǒng)計。從圖中可看出，所統(tǒng)計的狀態(tài)點中，周向畸變指數(shù)在綜合畸變指數(shù)中的比例基本處于40%～60%區(qū)間。根據(jù)綜合畸變指數(shù)公式可以推出，紊流度在綜合畸變指數(shù)中所占的比例為40%～60%，考慮到±10%的畸變流場壓力測試精度，可認為周向畸變指數(shù)約等于紊流度。據(jù)此，當壓氣機由于結構原因無法布置動態(tài)總壓測點時，可用兩倍周向畸變指數(shù)的方式近似得到綜合畸變指數(shù)，進而評定壓氣機的抗畸變敏感性；同時，還可利用這一結論判別紊流度的粗大誤差。

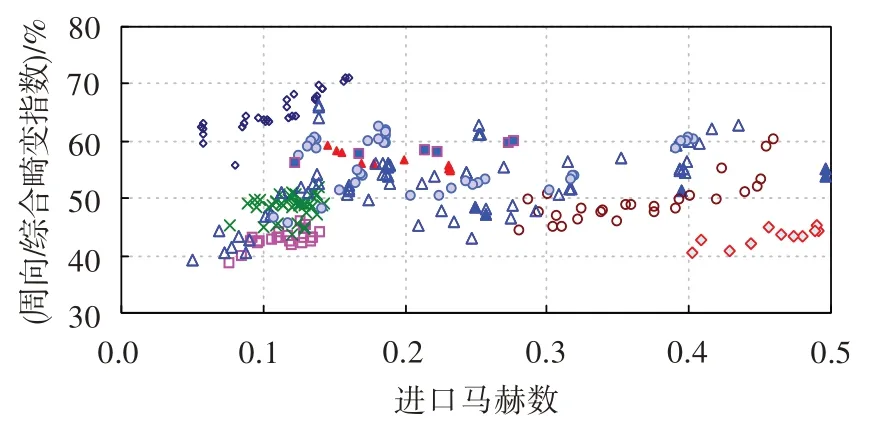
圖7 周向畸變指數(shù)在綜合畸變指數(shù)中所占比例Fig.7 The proportion of circumferential distortion index in comprehensive distortion index

4 結論

(1) 進氣道直徑大小對畸變特性基本無影響，可忽略。

(2) 建立了基于試驗數(shù)據(jù)不完全統(tǒng)計規(guī)律下畸變指數(shù)與插板幾何特性的關聯(lián)模型。該模型已用于指導壓縮部件進氣畸變試驗方案的制定，并將試驗效率提升了1 倍。試驗過程中，當需要調(diào)整壓氣機進口畸變強度時，采用更換插板深度的方式比改變距離更容易達到目的。

(3) 周向畸變指數(shù)在綜合畸變指數(shù)中的占比為50%±10%，當壓氣機由于結構原因無法布置動態(tài)總壓測點時，可用兩倍周向畸變指數(shù)的方式近似得到綜合畸變指數(shù)。

(4) 由于數(shù)據(jù)有限，本文所建立的綜合畸變指數(shù)與進口馬赫數(shù)的關聯(lián)模型還存在很寬的區(qū)域(圖3中的虛線)需要驗證，在以后工作中應使用更多的試驗數(shù)據(jù)對各關聯(lián)模型進行修正完善。