基于瞬時銑削力系數法的拼接模具銑削穩定性研究

岳彩旭，郝小樂，王彥武，高海寧，馬 晶，馮 磊

(1.哈爾濱理工大學 機械動力工程學院，哈爾濱 150080;2.哈爾濱理工大學 先進制造智能化技術教育部重點實驗室，哈爾濱 150080)

汽車覆蓋件模具加工過程中，由于部分零件表面形狀復雜多變，在局部位置上有特殊的硬度要求，致使模具型腔凹凸不平。需要根據零件不同部位受力、受熱特征采用不同硬度的模具拼接而成，將不同硬度的鑲塊分離淬火后再拼接成整體件來保證模具的輪廓精度，并改善模具的加工工藝。由于不同硬度工件拼接的影響致使銑削拼接過縫處時銑削力幅值明顯變化并加劇振動，進而降低工件表面質量和刀具的使用壽命，如何在拼接過縫處平穩過渡是亟待解決的問題。為此，本文提出基于瞬時銑削力系數法的銑削穩定性預測模型，來解決銑削拼接模具過程的振動問題，該預測模型可以為大型汽車覆蓋件銑削加工提供理論參數依據。

獲得銑削力系數是完成銑削穩定性預測研究的基礎，針對銑削力系數研究方法國內外學者從多方面進行探究，其中Gonzalo 等[1-2]對銑削力系數隨切削參數變化規律深入研究，得到了切削力系數與瞬時切厚、傾角的關系表達式，并結合試驗與理論驗證該方法的優勢。Campatelli等[3]提出了銑削力系數隨速度變化的規律，研究結果表明切削力系數在低速區數值偏大，在高速區數值先減小后增大。Grossi等[4]利用傳統的平均力法和基于遺傳算法的瞬時估計法得到銑削力系數。最后驗證表明瞬時估計法更加準確有效。Wang等[5]通過平均銑削力法結合槽切試驗得到切削力系數，研究了切削參數對銑削力系數的影響規律，得出在主軸轉速(500～1 500 r/min)范圍內切削參數不影響切削力系數的結論。岳彩旭等[6]基于動態銑削力系數法結合改進的半離散時域方法仿真得到銑削過程穩定性預測曲線。Gonzalo等[7]提出一種能夠預測瞬時銑削力模型，在綜合考慮了刀具材料屬性、切削參數以及刀具幾何等因素，得到的模型較平均法的預測精度高5%。

在研究銑削穩定性時多用穩定性葉瓣圖來判斷是否發生顫振，穩定性葉瓣圖的邊界是由臨界切削深度和主軸轉速關系繪制的預測曲線，顫振預測模型方法主要分為頻域法、離散法、數值法等。在利用頻域法求解銑削穩定性顫振模型方面諸多學者對此進行了研究，Altintas[8]建立了多自由度動力學模型，提出了零階求解法，通過求解特征方程根獲得無顫振發生下的臨界銑削深度，該方法計算效率高，但精度較低。Merdol等[9]在零階求解法的基礎上提出了多頻率法，綜合考慮了定向因子的高次諧波以及刀具-工件間的傳遞函數，提高了頻域法的計算精度。Bachrathy等[10]將多頻率求解法應用到動態特性研究中，不僅考慮了時滯因素影響，而且將二分法與多頻率法進行結合，又進一步提高了頻率法的計算效率與計算精度。離散法可分為全離散法、半離散法、有限元法等。宋清華等[11]采取半離散方法利用共振區半帶寬理論研究了穩定性預測曲線與工件表面質量的關系，通過試驗綜合驗證分析了共振區的穩定性預測曲線的精度。李忠偉等[12]運用Magnus-Gaussjan截斷法來獲得不同參數條件下的銑削穩定性葉瓣圖，在提高了原半離散法的計算精度的基礎上，又減少了仿真的計算時間。全離散首先由Ding等[13]提出，運用了數值積分的方法對時滯周期等分離散，再求解振動微分方程的特征值，根據Floquet理論判斷是否發生顫振。Liu等[14]綜合考慮了復雜曲面特征以及刀具前傾角對瞬時切屑厚度影響等因素，利用全離散法得出了曲面特性對穩定性時域的影響關系。Bayly等[15]分別進行了單、雙自由度動力學建模研究，主要對銑刀是否參與切削所導致的動力學變化而進行深入研究。后續Ding等[16-18]通過運用時間有限元方法，將有限元法改進成考慮再生效應等延遲項的半解析方法來預測銑削穩定性，重新建立了隨周期系數矩陣變化的積分表達式。Liang等[19]提出了一種改進的數值積分法，基于變化時間延遲，利用偏移矩陣對Floquet過渡矩陣進行修改，得到時滯對穩定性變化影響趨勢。

在上述銑削穩定性研究中，多數采用平均銑削力系數法來獲取仿真所需的銑削力系數，由于拼接模具銑削過程存在不同硬度拼接及切入沖擊，致使銑削力幅值增大，隨著加工的進行銑削力幅值逐漸減小，為此拼接模具銑削過程銑削力系數是變化的，而平均銑削力系數不能體現該過程，所以本文采用瞬時銑削力系數法。基于瞬時銑削力系數法所得到的穩定性預測曲線分為上下限兩部分，每部分存在多條預測曲線，選擇任意一條上下限預測曲線不能準確預測銑削系統是否發生顫振，故本文利用最小包絡法來得到極限穩定域，根據上下限選取各個穩定性葉瓣的最低包絡點以形成的最小包絡葉瓣帶作為最終的穩定邊界；最后通過時頻域分析綜合驗證模型的準確性，其結果可以為大型汽車覆蓋件銑削加工過程提供理論參數依據。

1 拼接過縫處切厚模型

在動態銑削過程中，當刀具與工件接觸而產生振動，每一刀齒都會留下振紋，當下一刀齒切入時會再次產生波動。銑削振動影響瞬時變化的銑削厚度，而且前一刀齒波動也會影響。建立拼接模具銑削過程的瞬時切厚模型需要先劃分銑削區域，根據單硬度區域、多硬度區域來分段式求解瞬時切削厚度。

1.1 銑削區域的劃分

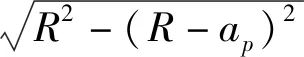
(1)

由式(1)可知，當0≤t≤td時，在同時銑削相鄰兩個不同硬度工件時，銑削過程由60HRC工件切向50HRC工件，取銑刀螺旋刃上的一點P，切削區域的劃分示意圖如圖1所示。

可以根據P點的位置來判斷銑削厚度，可以分成兩種情況：第一種為P點處在銑削高硬度60HRC區域(第一硬度區域)；第二種為P點處在銑削低硬度50HRC區域(第二硬度區域)。設定沿進給方向上P點距切削圓中心軸線的距離表示為Rp=Rsinθjisinκ。以此可以得到當前刀齒的P點距拼接縫的距離dj，表示為

(2)

圖1 切削區域的劃分示意圖Fig.1 Division of cutting areas

當dj≥0時，則P點處在銑削單一硬度(低硬度)50HRC區域。否則，P點處在單一硬度(高硬度)60HRC區域。

1.2 拼接過縫處的切削厚度

切削厚度可以表示為hs，前一刀齒軌跡距拼接處的距離dj-1表達式為

dj-1=dj-hssinκ

(3)

hs=fzsinθjisinκ

(4)

當dj-1<0時，同時銑削兩種硬度工件，此時切削厚度需要分兩段來計算，hs1和hs2分別表示P點在過縫前后的切削厚度，如圖2所示。

(a)切厚三維示意圖

(b)切厚平面示意圖圖2 切厚三維示意圖Fig.2 Three-dimensional sketch of cut thickness

圖2中|PP1|即為切屑厚度。

根據上述靜態厚度表示為hs，當前刀齒軌跡P點距拼接處的距離為dj，可以得到

(5)

則該點的三個方向銑削力公式根據切厚的表達式不同需要分段來計算，拼接區域的切向、徑向和軸向的銑削力表達式，將上述公式轉化為X、Y、Z三個方向銑削力公式為

(6)

當dj≤0時，則P點處在銑削單一硬度(低硬度)60HRC區域。則該點的銑削力在X、Y、Z方向的表達式為

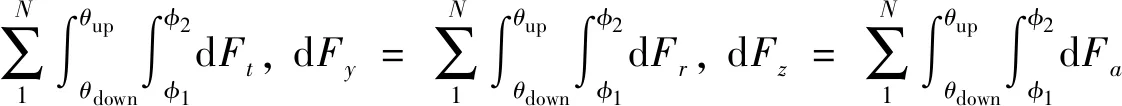
(7)

式中：N為齒數；φ1、φ2分別為第j齒參與切削時最小、最大位置角。

確定φ1、φ2、φ3、φ4的值，首先要明確P點與刀具幾何軸線的距離，點P1，P2，P3和P4分別處在切削刃上三個不同區域的交界處。P1和P4位置角度可以表示為

(8)

在P2處，點P2到拼接縫的距離為零，即dj=0，可以根據式(9)確定φ2。

(9)

在點P3處，前一刀齒軌跡距拼接過縫處的距離為0，則可以根據公式(10)確定φ3。

(10)

上述公式推導出拼接區域的靜態切厚，動態銑削過程需考慮再生效應，前后兩刀齒由于相位差引起的動態切厚hd表達式為

hd=(vj-vj-1)sinκ

(11)

式中：vj和vj-1分別表示前后兩刀齒留下的振動位移，然而，在大振幅的情況下，第(j+1)刀齒不與已加工表面接觸，而vj可能是第(j+2)刀齒留下的振動位移，甚至第(j+3)、第(j+4)刀齒。這是由動態銑削過程的非線性導致的，因此vj可表示為

vj=min {vj+1(t-T),vj+2(t-2T)+h,vj+3(t-T)+2h,…}

(12)

t為當前時間，T為連續刀齒運動周期，因為切屑厚度在徑向進行測量的，vj轉變為X、Y方向為

vj=Δxsinθji+Δycosθji=

[x(t)-x(t-T)]sinθji+[y(t)-

y(t-T)]cosθji

(13)

其中Δx=x(t)-x(t-T)，Δy=y(t)-y(t-T)分別表示為X、Y方向前、后刀齒所產生的動態位移。時滯周期T表達式為T=60/(Nt·n)。

由靜態切厚、動態切厚共同構成未變形瞬時切屑厚度h，可表示為

h=(hs+vj-vj-1)g(θj)

(14)

其中g(θj)為判斷刀具是否參與切削的函數。刀齒j的銑削力是關于銑削力系數、銑削深度和切屑厚度的函數關系式，公式為

(15)

2 銑削過程的瞬時銑削力系數法的求解

準確獲得銑削力系數是得到銑削穩定性預測仿真模型的關鍵。銑削力系數求解研究方法大體分為兩種：① 基于直角切削數據庫通過參數轉換來獲取斜角銑削力系數方法；② 利用快速標定的方法來獲取斜角銑削力系數方法。第二種求解銑削力系數的方法又可分為平均銑削力系數法和瞬時銑削力系數法兩種。本文所采用的是瞬時銑削力系數法，該方法是在時域部分用最小二乘法擬合仿真結果和試驗結果，通過反演的方法來獲取銑削力系數。

瞬時銑削力系數求解法利用非線性最優化方法解決最小二乘曲線擬合的問題，并考慮到目標函數定義的上限和下限變量，優化過程使用最小二乘算法，時域仿真的銑削力等同于在每個時間步內測量的銑削力。

在每一個小的時間步dt時域仿真計算銑削力，dt的求解公式為

(16)

式中：fs是銑削力測量過程的采樣頻率。在每一個時間周期計算瞬時切屑厚度和切削力，刀齒旋轉角度為φ，dφ由時間步數和主軸轉速決定。瞬時切屑厚度由刀具圓弧路徑近似而成，并假設刀具和工件是剛性的。銑削力可以分為切向力Ft、法向力Fn和軸向力Fa，為了得到仿真結果，需將三個方向銑削力進行坐標系轉換，表示為

(17)

ds為每一離散單元的切削刃長度，h是未變形切屑厚度，db是每一離散單元的切屑寬度。瞬時銑削力系數是根據仿真銑削力和測量銑削力來計算的，公式可表示為

[A(t,θ,κr,h,S)]{Ktc,Kte,Krc,Kre,Kac,Kae}

(18)

把仿真銑削力和試驗測量銑削力在t時等同化，方程轉變成

[A(t,θ,κr,h,S)tn]{Ktc,Kte,Krc,Kre,Kac,Kae}

(19)

其中Φ是刀具瞬時旋轉角，目標函數被定義為

(20)

其中k是決策變量的向量，包括6個具體的銑削力系數，目標函數在每一時間步仿真力和測量力是不同的。

因為每個模擬瞬時銑削力的時間步長必須和測量時的銑削力是一致的，所得到的方程組取決于采樣頻率(即時間步數)，求解公式表示為

fn(k)2)

(21)

n是時間步數，曲線擬合問題通過反射算法來解決，常用于求解決策變量的上限或下限。測得的平均銑削力分別用于包括一些相關工藝參數的非線性優化函數，其中參數包括刀具的齒數、銑削力的測量采樣頻率和決策變量。此處求得不同硬度下銑削力系數將為后期穩定性預測曲線的編程提供參數基礎。

3 拼接模具銑削過程穩定性研究及算法分析

根據球頭銑削加工特點建立了銑削過程的動力學模型，求解動力學方程時使用Li等[20]提出的基于四階Runge-Kutta法的全離散法(RKCDM)，此方法是在全離散法的基礎上，運用龍格庫塔迭代法離散時滯微分方程，簡化離散迭代公式的復雜性，提高了仿真的計算效率與計算精度，表現出較好的收斂性。

對于球頭刀銑削加工而言，通常都沿X、Y平面進給，刀具受力主要為切向力和徑向力，軸向力一般忽略不計，因而建立兩自由度的銑削動力學模型。建立拼接模具銑削過程動力學模型時同時考慮了銑削單硬度區域的銑削力與拼接處切入切出的沖擊力，以球頭銑刀和工件作為研究對象，將刀-工接觸模型轉化為兩個垂直的彈簧阻尼等效模型，在主軸與刀具之間可以把在X和Y方向的微分方程描述為

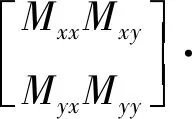
(22)

式中:Mxx、Myy為在X和Y兩方向的模態質量；Cxx、Cyy為在X和Y兩方向的模態阻尼；Kxx、Kyy為兩方向的模態剛度；忽略銑刀X和Y向的結構模態耦合效應，即假設式中Mxy、Myx、Cyx、Cxy、Kxy、Kyx均為0；總切削力分成單一硬度區的銑削力F(t)和拼接處的沖擊力F(t)impact兩部分。

將上述銑削動力學公式轉化為考慮時滯性的二維銑削時滯微分方程為

(23)

式中：ωnx、ζx、kx、ωny、ζy、ky分別表示為X、Y方向上的固有頻率、阻尼比、剛度系數；ap是軸向切削厚度；Kt是切向的切削力系數；T是刀齒通過周期；x(t-T)和y(t-T)是時滯項。

g(φj(t))=(2πΩ/60)t+2π(j-1)/N

(24)

式中：Ω是主軸轉速，單位為r/min；g(φj(t))為判斷刀齒j是否參與切削的函數，被定義為

(25)

式中，φst和φex分別表示刀齒j的切入角、切出角。逆銑時，φst=0且φex=arccos(1-2a/D)；順銑時，φst=arccos(2ae/D-1)且φex=π，ae/D表示徑向浸入率(ae是徑向切削深度，D是球頭銑刀的直徑)。

將式(17)轉換到空間形式為

(26)

其中A(t)和B(t)表示時間周期系數矩陣，則A(t)=A(t+T)，B(t)=B(t+T)，T是時間周期，其數值與時滯量相等。τ是時滯時間，在T=τ時為單延遲銑削過程。為了解決A(t)和B(t)，本節使用四階龍格庫塔方法，時間周期T等距離散成m個時間段(m為整數)，每段時間周期為Δt，T=mΔt，m為單齒通過周期的離散數，由經典Runge-Kutta表示成

(27)

式中，ui表示u(i·Δt)，ui+1表示u[(i+1)·Δt]，ti表示idt，變量i為整數且滿足0≤i≤m。使用龍格庫塔方法，公式依次推導得

(28)

ut+1=Fi·ui+Fi-m·ui-m+Fi-m+1·ui-m+1

(29)

其中系數Fi，Fi-m，Fi-m+1表示為

(30)

其中I是n×n單位矩陣，n是矢量ut的維數。

為了獲得傳遞矩陣，n×(m+1)維度矢量公式為

zi=col(ui,ui-1,…,ui-m+1,ui-m)

(31)

由上式能得到傳遞方程表達式為

zi+1=Dizi

(32)

因此系數矩陣Di作為一個Di(2m+4)維度矩陣，當i=0,1,…,k-1，(2m+4)維傳遞矩陣φ表示為

φ=Dk-1·Dk-2…D2·D1

(33)

根據Floquet理論，如果傳遞矩陣φ的特征方程根有一個大于1，則系統是不穩定的，否則系統是穩定的。因此邊界曲線在穩定性圖表中被分為穩定區域和不穩定區域，能作為判定是否發生顫振的依據。

4 銑削試驗及結果分析

4.1 銑削力系數試驗

在拼接區域同一刀齒同時切削兩種不同硬度材料，為獲得表示該過程切削力系數，基于每一刀齒切削力數據，采用最小二乘曲線擬合法得到瞬時銑削力系數。

試驗所需裝置包括：奇士樂旋轉測力儀，數據采集箱，奇士樂5070A電荷放大器；試驗所需工件：硬度為50HRC、60HRC拼接工件。試驗所需的刀具為：直徑φ=20 mm的刀片式球頭銑刀；所需的機床是大連機床VDL-1000E立式四軸加工中心。由于銑削平面工件時球頭銑刀刀尖的切削速度為0，所以進行銑削力系數試驗時，將工件傾斜放置，傾斜角為：20.4°，如圖3(a)、(b)分別為銑削力系數辨識試驗所用的數據采集儀、電荷放大器和旋轉測力儀。銑削力系數試驗機床與工件擺放位置圖如圖4。

(a)數據采集儀與電荷放大器

(b)旋轉測力儀圖3 銑削力系數辨識試驗所用的儀器Fig.3 Machines and equipment of milling experiment

圖4 銑削試驗機床與工件擺放布局Fig.4 Milling test machine and workpiece placement layout

此節求得不同硬度下銑削力系數將為后續穩定性預測曲線的編程提供參數基礎。

得到拼接區域瞬時銑削力系數的平均值如表1所示，不同切削參數對銑削力系數的影響規律見4.2節。

表1 拼接區域瞬時銑削力系數Tab.1 Instantaneous milling force coefficient of splicing area

4.2 切削參數對瞬時銑削力系數的影響

4.2.1 主軸轉速的影響

本節主要針對主軸轉速因素進行了一系列銑削試驗，并使用瞬時銑削力法求解銑削力系數，保持每齒進給量0.08 mm/tooth、銑削深度0.2 mm保持不變，并選取的主軸轉速范圍為2 500～6 000 r/min，每次增加的步長為500 r/min。

圖5中的三條折線為利用平均銑削力系數法得到的銑削力系數隨主軸轉速的變化趨勢，并利用瞬時銑削力法得到每個主軸轉速下銑削力系數的最大值、最小值。圖中銑削力系數有一個顯著的下降趨勢直到臨界主軸轉速達到4 500 r/min，當超過臨界轉速4 500 r/min時，銑削力系數有明顯上升的趨勢，然后平穩。銑削力系數出現下降的趨勢歸因于高速銑削條件下刀具與切屑相互作用導致溫度上升進而導致工件材料出現熱軟化的現象。

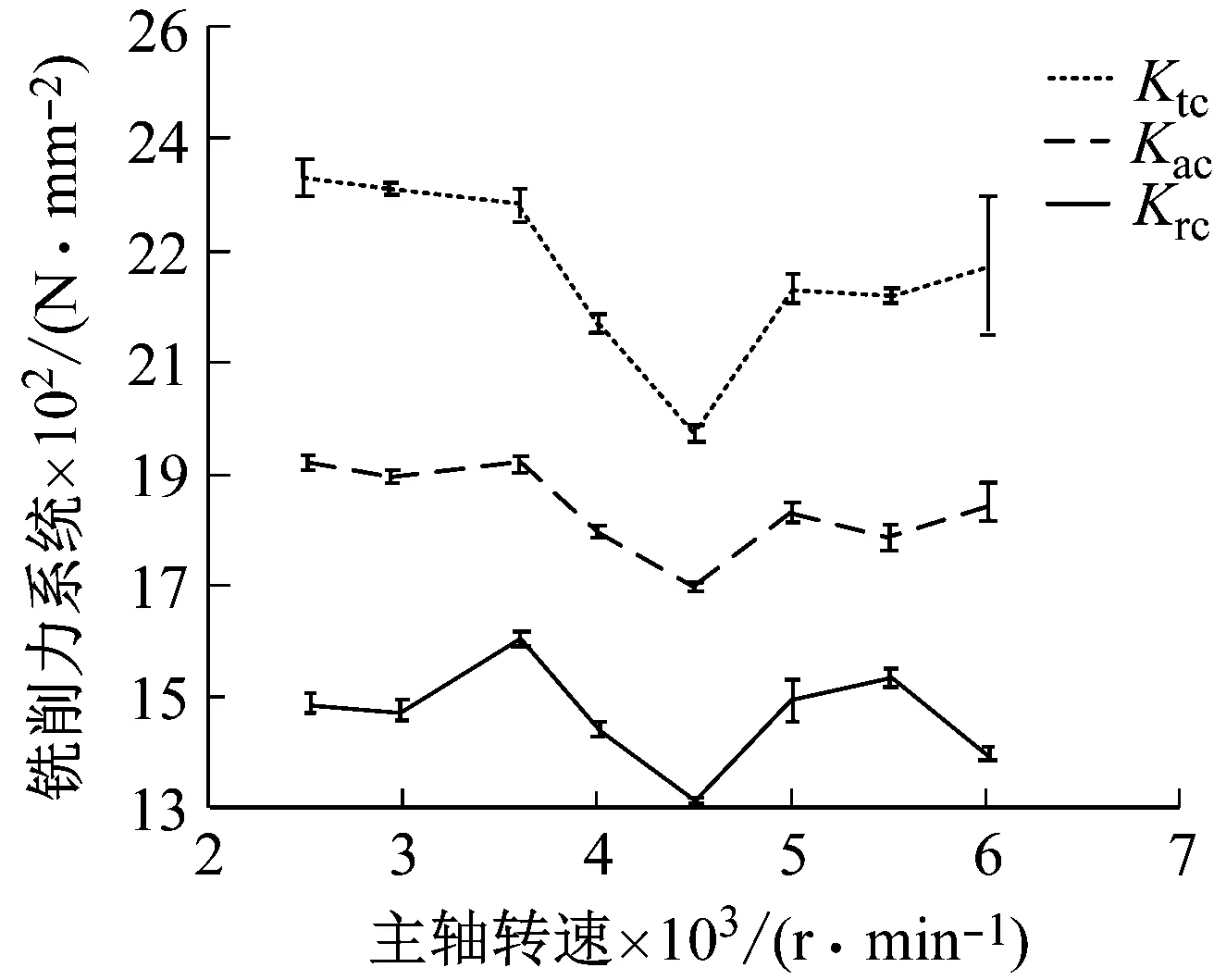
圖5 主軸轉速對銑削力系數的影響Fig.5 Effect of spindle speed on milling force coefficient

4.2.2 每齒進給量的影響

本節主要針對每齒進給量因素進行了一系列銑削試驗，并結合使用平均銑削力系數法以及瞬時銑削力法求解銑削力系數，保持主軸轉速4 000 r/min、銑削深度0.2 mm不變，并選取的每齒進給量的范圍為：0.05～0.25 mm/tooth，每次增加的步長為0.05 mm/tooth。

圖6是在逆銑條件下得到的銑削力隨每齒進給量變化的趨勢示意圖，其中的三條折線為利用平均銑削力系數法得到的銑削力系數隨每齒進給量的變化趨勢，并利用瞬時銑削力系數法得到每齒進給量下銑削力系數的最大值和最小值。從圖中可以發現切向銑削力系數和法向切削力系數隨著每齒進給量的改變呈現無規則降低的趨勢。然而徑向銑削力系數沒有顯著變化。同一參數條件下進行順銑試驗，發現不同銑削方向的銑削力系數變化趨勢是相一致的。

圖6 每齒進給量對銑削力系數的影響Fig.6 Effect of feed per tooth on milling force coefficient

4.2.3 銑削深度的影響

由于球頭銑刀每一刀齒參與切削區域的不斷變化導致瞬時未變形切屑厚度受每齒進給量和銑削深度的影響。當每齒進給量保持固定，銑削深度減小，則瞬時未變形切屑厚度也減小，為了研究徑向銑削深度對特定銑削力系數影響，銑削深度設定為0.2～1 mm，每次增加的步長為0.2 mm。保持主軸轉速4 000 r/min、每齒進給量0.08 mm/tooth不變情況下來進行一系列銑削試驗，使用平均銑削力系數線性法和瞬時銑削力非線性法得到的瞬時銑削力系數結果如圖7所示。

圖7 銑削深度對銑削力系數的影響Fig.7 Effect of milling depth on milling force coefficient

從圖7可以發現，切向、法向和徑向銑削力系數隨著銑削深度的改變而顯著變化，即呈現不規則減小的趨勢，當銑削深度在0.1～0.6 mm之間銑削力系數隨著銑削深度逐漸減小，當超過0.6 mm銑削深度時銑削力系數基本保持不變。

4.3 拼接模具銑削穩定性分析

根據上述提出的穩定性預測分析方法，首先輸入銑削系統的X、Y和Z方向模態參數，并基于Runge-Kutta法的全離散法進行MATLAB仿真來獲得多硬度拼接模具銑削過程穩定性預測曲線。選取一階模態參數為ωnx=785 Hz，ωny=800 Hz，ωnz=753 Hz，ζx=0.024 6，ζy=0.026 3，ζz=0.021 5，kx=1.74×107N/m，ky=1.71×107N/m，kz=1.21×107N/m，計算步數選取m=40。由于瞬時銑削力系數隨著銑削參數的變化而變化，導致不同主軸轉速和切深下存在多條預測曲線，選擇任意一條上下限預測曲線不能準確預測銑削系統是否發生顫振，故本文利用最小包絡法來得到極限穩定域，根據上下限選取各個穩定性葉瓣的最低包絡點以形成的最小包絡葉瓣帶作為最終的穩定邊界。最小包羅法適用于任何硬度的拼接件，在獲得準確切削系數的前提下，借助于求解動力學的時頻域方法，獲得相應系數下的葉瓣圖，最后用最小包羅法得到穩定性葉瓣帶。利用最小包絡法得到穩定性預測曲線的步驟為：首先保持每齒進給量0.08 mm/tooth、銑削寬度0.15 mm、刀具參數不變的前提下選取四組切削參數：① 主軸轉速3 500 r/min、銑削深度0.15 mm；② 主軸轉速3 500 r/min、銑削深度0.2 mm；③ 主軸轉速4 000 r/min、銑削深度0.15 mm；④ 主軸轉速4 000 r/min、銑削深度0.2 mm，然后求解各組參數條件下的瞬時銑削力系數，得到每個參數條件下的瞬時銑削力系數的上下限，最終分別仿真上限和下限的穩定性預測曲線，通過MATLAB仿真可得到多硬度拼接模具銑削過程穩定性預測曲線如圖8所示。

圖8 銑削穩定性葉瓣圖Fig.8 The milling stability lobes

圖8中上部四條曲線、下部四條曲線分別為利用四組切削參數求解的瞬時銑削力系數繪制的上、下限穩定性葉瓣，上、下方粗曲線是利用最小包絡法得到的穩定性預測曲線，兩粗曲線中間區域為臨界穩定區域，即區域內不是所有點都是穩定或不穩定的點，上方為不穩定區域，下方為穩定區域。

4.4 銑削穩定性預測結果的試驗驗證

根據利用最小包絡法得到穩定性葉瓣曲線，選取局部點進行銑削顫振試驗，主軸轉速選取的范圍為2 000～8 000 r/min，每次增加的步長為1 000 r/min，銑削深度選取的范圍為0.1～0.6 mm，每次增加的步長為0.05 mm。選用銑削試驗機床是大連機床VDL-1000E立式四軸加工中心進行，試驗所用的信號采集系統采用的東華DH5922，采用的測力儀為Kistler旋轉測力儀，銑削顫振試驗的儀器與銑削力系數試驗儀器相同。試驗所用的刀具為φ=20 mm刀片式球頭銑刀，齒數為2，刀具裝夾懸伸長度220 mm，工件采用硬度為60HRC、45HRC拼接而成的淬硬鋼Cr12MoV。

圖9為多硬度拼接淬硬鋼銑削穩定性預測曲線的示意圖，在圖中選取四個參數點進行試驗驗證，選取四點的切削參數分別為A(n=4 000 r/min，ap=0.1)、B(n=4 000 r/min，ap=0.3 mm)、C(n=5 500 r/min，ap=0.3 mm)、D(n=4 000 r/min，ap=0.6 m)，利用時域振動加速度以及傅里葉變換后的頻譜分析綜合驗證繪制穩定性預測曲線的準確性。

圖9 多硬度拼接淬硬鋼銑削穩定性預測曲線圖Fig.9 Prediction curve of milling stability of multi-hardness splicing hardened steel

圖10(a)、(c)、(e)、(g)分別為A、B、C參數點的振動加速度信號，圖10(b)、(d)、(f)、(h)分別為A、B、C點的傅里葉變換頻譜圖，從圖10(a)、(b)可以清晰看出A點的振動加速度波動平穩，幅值為6 m/s2，在傅里葉變換后頻譜分析的最大幅值對應的頻率為266.66 Hz是刀齒通過頻率(4 000×2/60=133.33 Hz)的倍頻，綜上分析可以判斷A點為穩定切削參數。從圖10(c)、(d)可以看出B點的幅值有短暫的波動，波動幅度不大，幅值基本維持在9.5 m/s2，較A點高出3.5 m/s2，但從頻譜圖中最大幅值對應的頻率為266.66 Hz可以看出，該頻率是刀齒通過頻率的倍頻，不是顫振頻率，綜合分析判斷B點是穩定切削參數；B、C兩點是同一切深不同轉速條件下兩點，圖10(e)、(f)中可以看出C點的振動加速度幅值突變較B點明顯，波動的最大加速度幅值達到19 m/s2，且頻譜圖中最高幅值所對應的頻率既不是刀齒通過頻率也不是其倍頻，該頻率為顫振頻率，綜上分析C點為不穩定切削參數；由于B、C兩點處于同一區域，但是通過分析得到該兩點一個是穩定切削條件，另一個為不穩定切削條件，故可以得出預測曲線上下限之間區域是臨界穩定區域。從圖10(g)、(h)中可以看出D點的振動加速度幅值突變明顯，且幅值較大，波動的最大加速度幅值達到21 m/s2，最終幅值穩定在15 m/s2，且頻譜圖中最高幅值所對應的頻率2 000 HZ既不是刀齒通過頻率也不是其倍頻，該頻率為顫振頻率；綜上分析D點為不穩定切削參數。通過對A、B、C、D四點的時域、頻域分析，可以得出本文所建立的穩定性預測曲線是準確的。

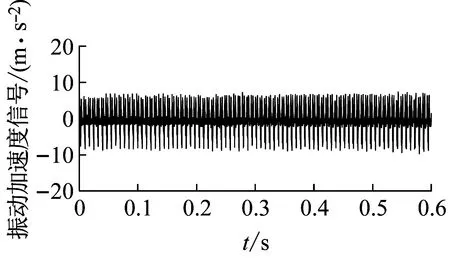
(a)A點的振動加速度信號圖

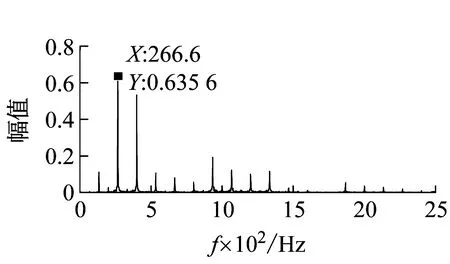
(b)A點的傅里葉變化頻譜圖

(c)B點的振動加速度信號圖

(d)B點的傅里葉變化頻譜圖

(e)C點的振動加速度信號圖

(f)C點的傅里葉變化頻譜圖

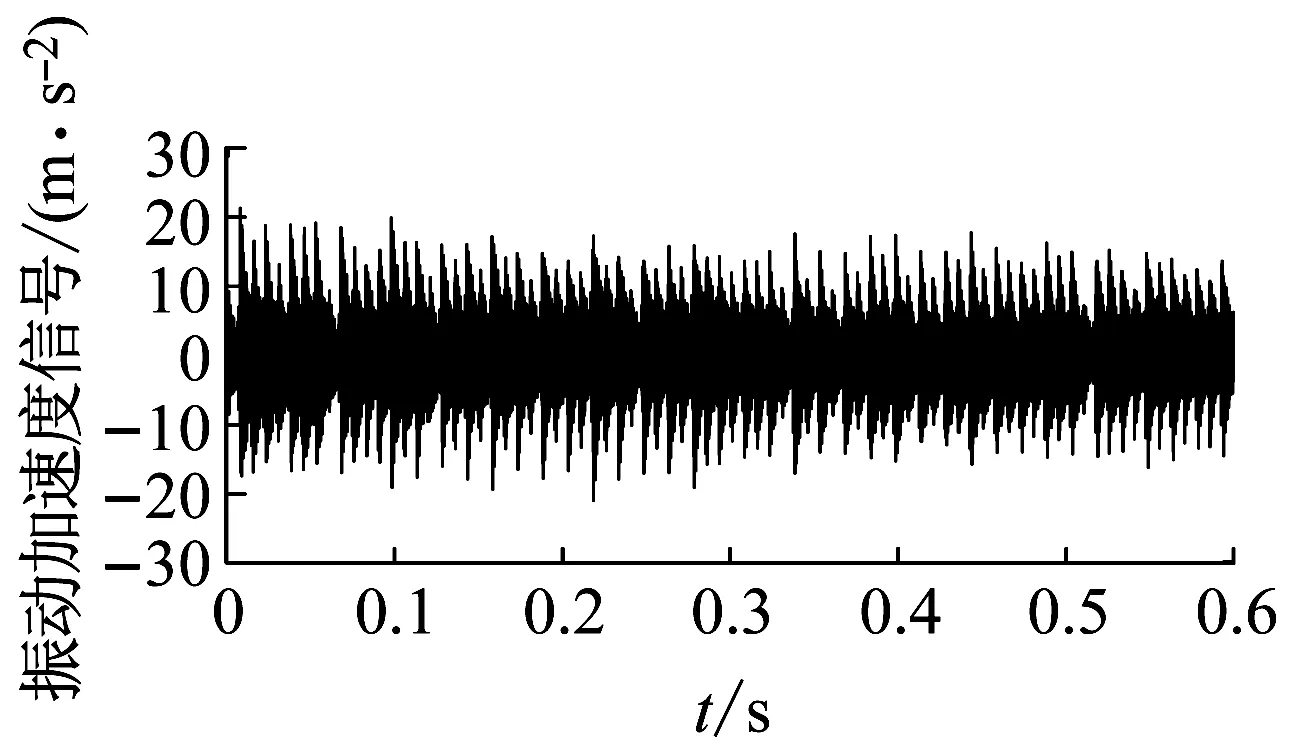
(g)D點的振動加速度信號圖

(h)D點的傅里葉變化頻譜圖圖10 A、B、C、D四點銑削試驗驗證圖Fig.10 Milling test verification diagram at A,B,C,D four points

5 結 論

在拼接模具銑削過程中，針對拼接過縫區域振動突變問題，本文分別建立拼接過縫處的瞬時切削厚度模型、基于瞬時銑削力系數法的銑削穩定性預測模型來深入研究拼接模具銑削過程振動特性，仿真時使用基于Runge-Kutta法的全離散法來實現穩定性預測，該方法計算速度快、精度高，并通過銑削顫振試驗來驗證穩定性預測曲線的準確性，綜上得到以下結論：

(1)從切削參數對瞬時銑削力系數影響研究可以得出：隨著每齒進給量與銑削深度的增加，瞬時銑削力系數的上下限都逐漸降低；但隨主軸轉速的提升，瞬時銑削力系數的上下限呈現先下降后上升最后平穩的趨勢。

(2)運用基于瞬時銑削力系數法得到多條銑削穩定性預測曲線，并利用最小包絡法得到兩條預測曲線的上下限，兩條預測曲線中間區域為臨界穩定區域，上方為不穩定區域，下方為穩定區域。