一種改進的D-S 沖突證據合成方法*

徐孫慶，耿俊豹，魏曙寰，韋可佳

（1.解放軍92493 部隊60 分隊，遼寧 葫蘆島 125000；2.海軍工程大學動力工程學院，武漢 430033）

0 引言

Dempster［1-2］于1967 年提出的D-S 證據組合理論是比較有力的理論工具，它處理不確定信息融合的能力很強，可以處理由不知道所引起的不確定性。目前已經被廣泛應用于圖像處理、故障診斷、風險評估、技術狀態評估、模式分類等領域。

D-S 證據理論的核心是證據合成規則［3］。但是在某些領域，特別是證據沖突時，合成過程的正則化處理會產生與直覺相反的結果，合成規則失效［4］。自從Zadeh［5］發表文章指出沖突悖論問題后，證據沖突一直是研究熱點。目前，主要從兩個方面對D-S 證據理論進行改進。一方面是對組合規則進行修改，這方面解決的主要是如何分配沖突的問題，包括以什么比例將沖突分配給哪些子集的問題［6］。文獻［7］提出利用統一信度函數模型將全局沖突進行再分配。文獻［8］則是提出基于局部沖突及沖突焦元間分配的方法。這些改進方法都是基于識別框架是封閉、完整的情況；倘若識別框架不完整時，便無法有效地處理證據沖突［9］。文獻［10］認為得到一個有窮而且完備的識別框架在實際中不可能，因此，提出了開放識別框架的概念，利用可傳遞置信模型，將沖突分配給空集。另一方面是對證據源進行修改。這種改進方法的思路也主要有加權平均和證據折扣兩種方法［11］。文獻［12］提出將證據進行簡單的平均修改模型就是屬于比較經典的加權平均法，但是這種方法沒有考慮到證據間的相關性。為了對證據相關性進行衡量，文獻［13］提出了證據間距離函數的概念。文獻［14］進一步闡述了證據的不確定性，將其在合成過程中加以考慮來確定權重，但沒有對Dempster 規則進行進一步修正。

沖突證據的融合是一個亟待解決的問題，但是迄今為止還沒有一個能夠被學術界廣泛接受的改進方法，現有的改進方法都或多或少地存在一些不足。針對目前改進方案的不足，為了使其具有更快的收斂性和精確性，本文利用Pignistic 概率距離衡量證據間的沖突程度；其次，為了更加高效地利用證據的全局信息，引進證據間相似度、支持度、確定度、決策度以及可信度來共同確定證據的權重，合理地分配沖突在各命題的比例；再次，對存在沖突的證據進行修正處理。最后，再利用統一信度函數模型對證據進行合成。

1 D-S 證據理論及不足

1.1 D-S 證據合成方法

設E1，E2是給定識別框架Θ 上的兩個證據，m1，m2分別表示E1，E2的基本可信度分配，焦元分別為A1，…，Ai和B1，…，Bj，設

則，其合成規則為：

1.2 合成證據沖突問題

當證據存在沖突時，利用D-S 合成規則將無法很好地對證據進行融合，甚至會推導出與實際相矛盾的結果。

例1 假設識別框架Θ={A，B，C}，給定的兩個證據為：

根據合成規則，組合過程如表1 所示。

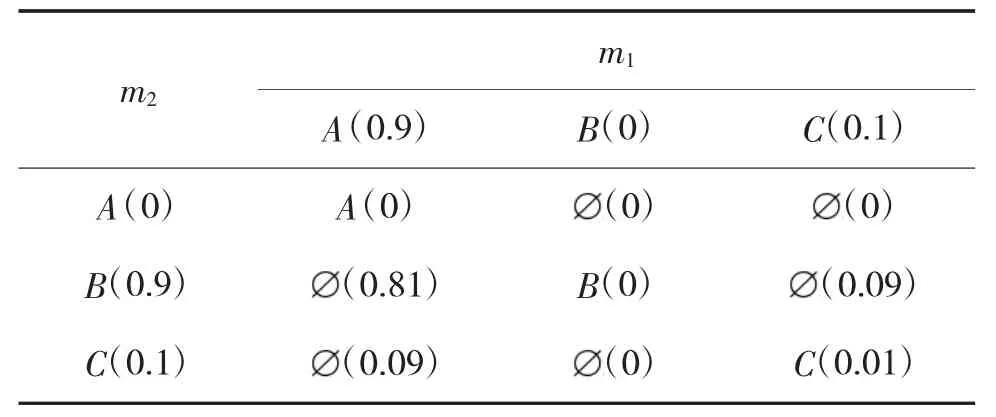
表1 D-S 組合規則運算表格

計算可得K=0.09+0.81+0.09=0.99，證據m1，m2高度沖突，分別支持A 和B，但合成結果為m（A）=（0）/（1-K）=0；m（B）=（0）/（1-K）=0；m（C）=（0.001）/（1-K）=1。融合后支持C，與常理不相符合，證據融合失效。

例2 假設識別框架Θ={A，B}，給定的兩個證據為：

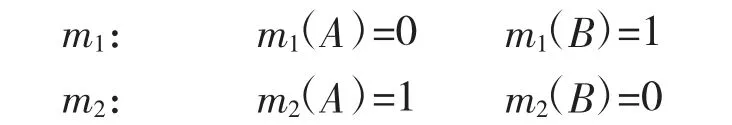
根據組合規則得K=1*1+0*0=1，證據完全沖突，無法利用經典組合規則進行證據融合。

2 典型的改進方法

目前對D-S 證據理論的改進主要有兩個思路，一個是從證據源模型進行改進，其代表方法是Yager 法。另一個是從合成規則進行改進，其代表方法是Murphy 法。

2.1 Yager 法

Yager 認為證據融合失效是由于組合規則的不足引起的，因此，假設識別框架是封閉的，將沖突部分全部分配給未知，其組合公式如下：

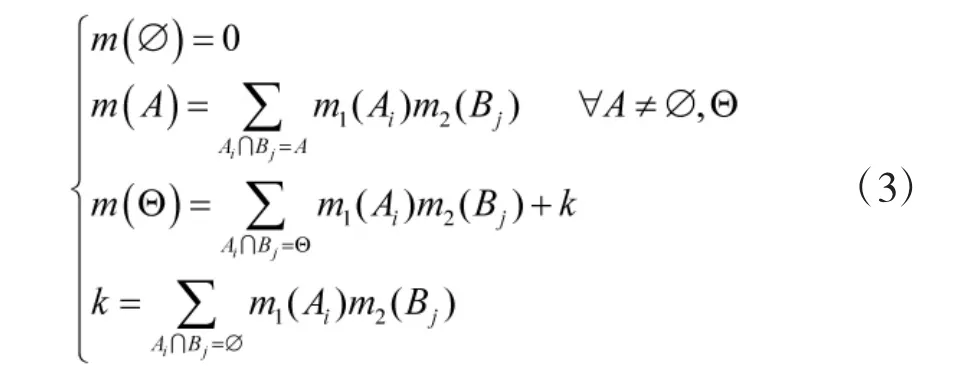
2.2 Murphy 法

Murphy 提出改進原始證據的方法以彌補D-S證據組合規則的不足。首先求出所有證據的基本概率分配值的算術平均，然后利用經典的D-S 組合規則進行n-1 次融合。該方法的計算過程如下：

3 一種新的證據合成方法

3.1 Pignistic 概率距離

目前用來表征證據沖突大小的主要有Pignistic概率距離、沖突率、Jousselme 距離、相關系數、相容系數等。根據文獻［15］研究，Pignistic 概率距離在表征沖突方面更加優勢，因此，本文選用Pignistic 概率距離表示證據沖突。

設m1，m2是同一識別框架Θ 下的兩個基本可信函數，用BetPm1，BetPm2分別表示它們的Pignistic概率函數。則它們的Pignistic 概率距離如下：

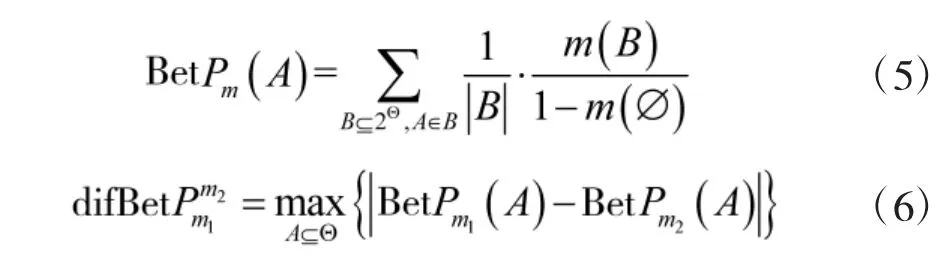
為了簡化計算過程，采用文獻［16］公式進行計算：

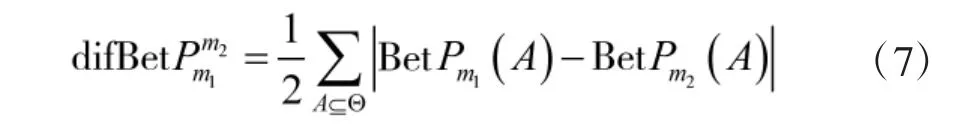
相似度是與距離相反的概念，根據文獻［13］定義，m1，m2的相似度表示為：

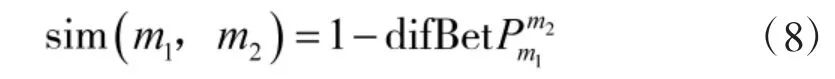
3.2 證據權重的確定

1）支持度

第i 個證據的支持度SD（i）定義為：

2）確定度

第i 個證據的確定度CD（i）定義為：

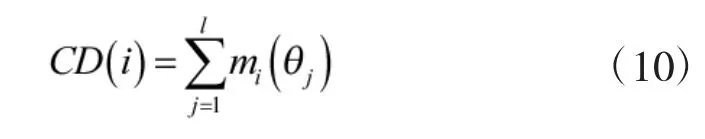
3）決策度

第i 個證據的決策度DD（i）定義為：

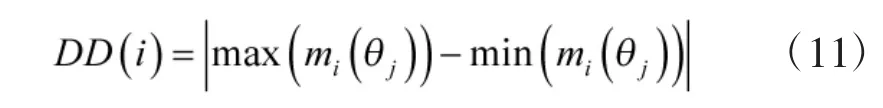
4）可信度

第i 個證據的可信度CRD（i）定義為：

記第i 個證據的權重為w（i），則第i 個證據的權重可以通過對可信度CRD（i）的正則化處理得到，為：

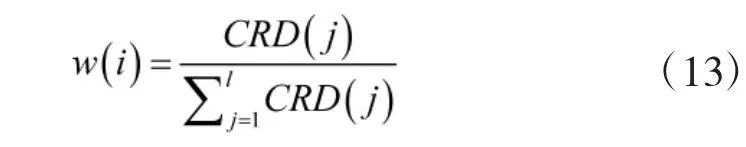
3.3 沖突證據的修正

通常情況下，當證據可靠時，各證據的權重相差不大，因此，可以利用上節得到的證據權重判斷沖突證據。假設有l 條證據，則這些證據的平均權重為w=1/l。若證據的權重w≥1/l，則認為該證據可靠；若證據的權重w＜1/l，則認為該證據不可靠，判定為沖突證據。利用折扣系數對沖突證據進行修正。

記第i 個證據的折扣系數為β（i），β（i）值如式（14）：

利用折扣系數，對沖突證據做如下修正：

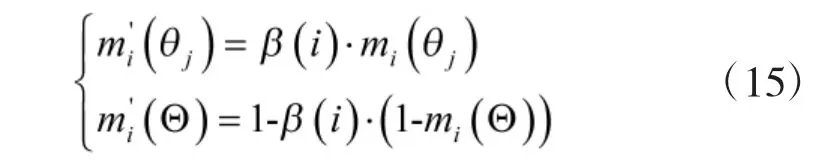
3.4 證據合成新公式

根據文獻［7］提出的統一信度函數組合模型，有：

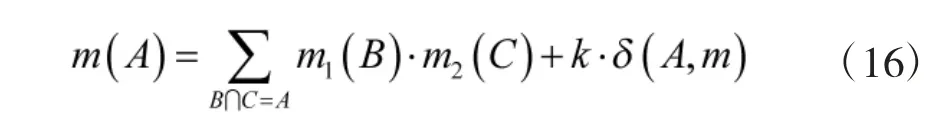
4 算例分析

為了驗證本文所提的改進方法的有效性及優越性，采用算例與傳統D-S 方法、Yager 方法、Murphy 方法進行對比計算。

例3 設識別框架為Θ={A，B，C}，給定的5 條證據如下頁表2 所示。根據上節所述求解過程，確定權重所需的各參數值如表3 所示。

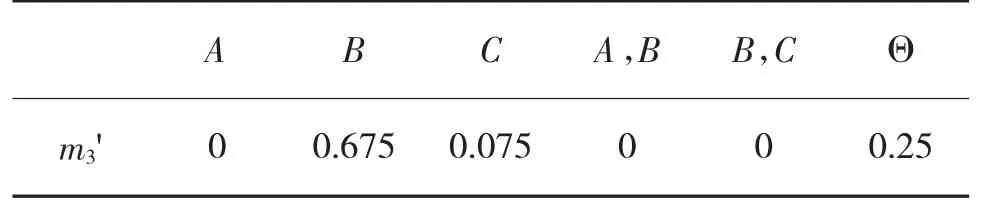
不難看出，第3 條證據高度支持B，和其他證據相沖突。根據表3 計算得，第3 證據的權重w（3）=0.15 小于平均權重=1/l=0.2，屬于沖突證據，需進行修正，與實際情況相符合。修正系數為β（3）=w（3）/=0.75，修正后的證據3 為：

?

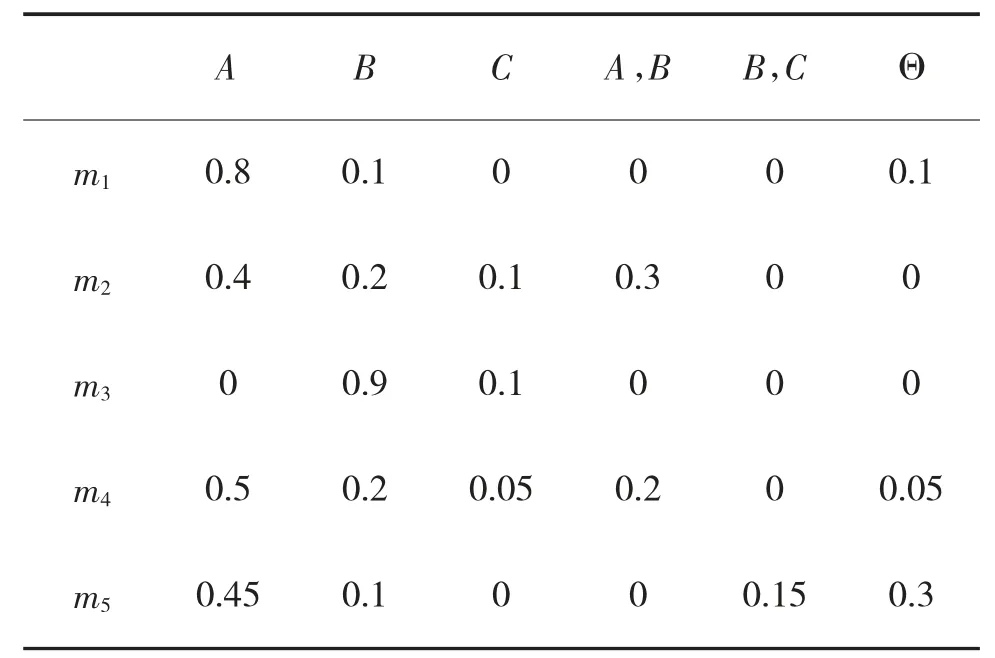
表2 識別框架下的5 條證據

根據所提出的證據合成方法進行證據融合對比計算，融合結果如表4 所示。

表3 各參數值

表4 4 種方法的融合結果對比

從表4 可以看出，當合成過程包含沖突證據3時，經典D-S 方法無法有效融合證據。即使大部分證據支持A，但是由于沖突證據3 的存在，導致融合結果顯示為支持B，與實際情況不相符合。同樣地，Yager 法在融合沖突證據3 時也是支持B，直接判定m（A）=0，不能很好地處理沖突證據。隨著后續證據的加入，m（A）值有所增大，但仍不能夠很好判斷出正確命題，而是將概率值分配給未知，增加了不確定性，未能判定出正確命題，融合結果過于保守。Murphy 法在處理證據3 時也出現了錯誤，以較大的概率值支持B，雖然后續能夠較好地處理證據沖突，能夠正確地判斷命題，但概率值較低，一直到第5 個證據的加入才能較為明確地判定出正確命題。而本文的方法能夠迅速得到正確的結果，即使在出現沖突證據3 時，仍能夠以較大的概率值判定出正確命題。本文方法在有效地利用證據的支持度、可信度、決策度的基礎上，能夠更好地利用證據的全局信息，能夠以更大把握選出正確命題。

為了更加直觀地感受各組合方法的融合效果，各方法m（A）的融合結果如圖1 所示。

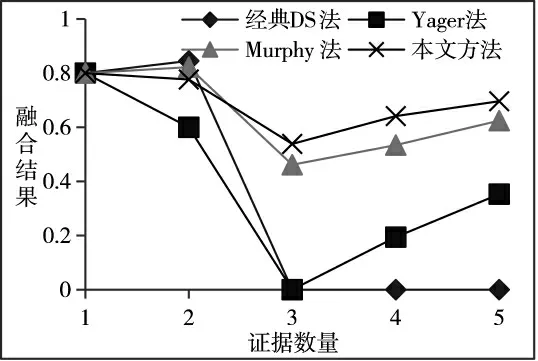
圖1 m（A）融合結果

從圖中能夠直觀地看出，經典D-S 法失效，不能正確融合證據；Yager 法、Murphy 在融合證據3 時也均出現了錯誤；本文方法在合成證據3 時仍能夠正確判斷出正確命題，魯棒性好，且在合成所有證據后以最高的概率值判斷出正確命題。

5 結論

為了更好地解決D-S 沖突證據的融合問題，本文提出了一種改進的D-S 沖突證據組合方法。首先引進Pignistic 概率函數判定證據的沖突程度，并得到證據間的相似度；其次，引進證據間的支持度、確定度、決策度和可信度4 個參量來共同決定各證據的權重，以便能夠更好地利用證據的全局信息。最后，通過算例與經典D-S 組合法、Yager 法和Murphy法進行對比分析，證明本文方法的有效性和可行性。

本文的方法對于多焦元命題的合成效果較好，對于單子集命題的合成結果較為保守，且默認識別框架是完整的，這些問題有待進一步研究。