基于估值修正的分布式傳感器網絡最小均方算法*

胡品端，熊慶國

（1.三峽大學電氣與新能源學院，湖北 宜昌 443002；2.武漢科技大學信息科學與工程學院，武漢 430081）

0 引言

由多傳感器節點（簡稱節點）組成的分布式無線傳感器網絡，能夠利用節點間的協作及信息互補實現魯棒監測，節點信息共享增強了其相關參數估計的準確性和抗干擾能力，在精準偵察、環境監測等實際工程中得到了廣泛應用［1］。

節點間信息共享時的參數估計性能，影響著其傳感器網絡能否快速準確地進行信息共享和系統魯棒性［2］。在傳感器網絡中，每個節點傳感器都具有一定的信息處理能力，但由于單個節點的能量、感知范圍、處理能力和抗干擾能力是有限的，借助多節點傳感器協作可有效提高對監測區信息估計的準確性和魯棒性。分布式傳感器自適應濾波網絡能夠自適應地迭代逼近未知向量，實現對信號的準確估計，有效繼承了自適應濾波與分布式器網絡的優異性能，將節點間的信息聯合互補計算與網絡的自適應收斂能力有機結合，成為分布式估計的研究熱點［3］。Takizawa［4］等人提出基于增量協作方式的增量最小二乘分布式自適應濾波，但其對節點的環形循環結構要求限制了其在大規模節點及復雜拓撲結構中的應用，于是又將擴散算法的策略與最小均方（Least Mean Square，LMS）算法結合，提出了擴散最小均方（Diffusion LMS，DLMS）算法，其簡單的分布結構要求和穩健性的算法性能受到廣泛關注，但其受到脈沖噪聲干擾時估計性能大大降低。Cattivelli［5］等人采用DLMS 算法實現分布式傳感器網絡的未知參數估計；BOUBOULIS［6］等人使用隨機傅里葉特征將擴散模型近似為固定大小的矢量，提出了一種基于網絡內核學習的擴散方案，并分析了漸近收斂條件和邊界值；張紅梅［7］等人基于改進的Sigmoid 函數構建DLMS 變步長調整策略，以緩解收斂速度與估計誤差間的沖突；Ni［8］等人基于誤差函數的符號函數化改進DLMS 算法，抗脈沖噪聲干擾性能優越［9］；張勇剛［10］等以最小化網絡均方誤差為準則，提出一種變階數自適應網絡濾波算法，以解決階數未知或時變時的參數向量估計，具有計算量小、可操作性強及估計精度高等特點。

在已有算法基礎上，為構建快速收斂和低穩態誤差，同時處理脈沖干擾的自適應濾波系統，設計了一種基于未知參數估計值p 階范數修正的最小均方自適應網絡濾波算法，在自適應變步長策略中引入參數估值的p 階范數，使得算法在收斂速度和穩態誤差方面平衡的同時具有較好的抗噪聲干擾能力，仿真實驗結果驗證了所提算法的性能和魯棒性。

1 擴散最小均方算法

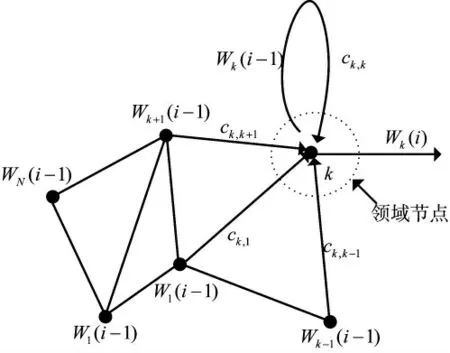
圖1 K 節點分布式傳感器網絡

對于網絡中第k=1，2，…，K 個節點，其輸出信號測量值可表示為：

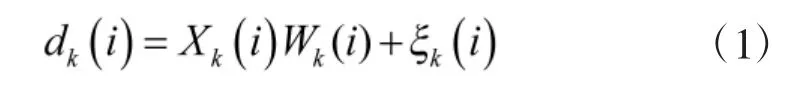
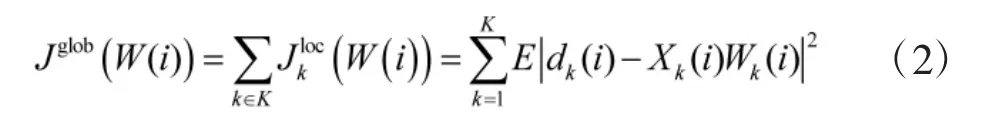
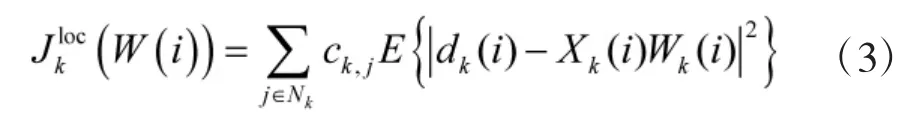
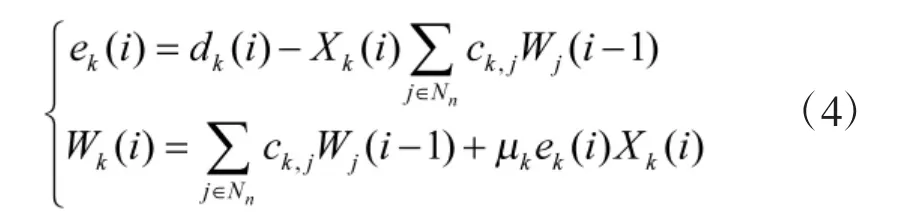
2 參數估值范數約束的LMS 濾波

在上一節算法基礎上，采用式（5）所示的局部目標函數［6］進行分布式自適應濾波

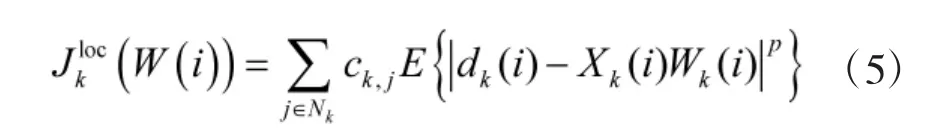
式中，通過估計誤差的p 階范數約束來提高算法對脈沖噪聲信號的抗干擾能力［6］，根據式（4），得到參數向量的迭代公式為：

式（6）換代增強了算法對脈沖噪聲信號的抗干擾能力，但仍需要解決收斂速度和穩態誤差之間的矛盾。文獻［7］指出，自適應濾波中步長調整即在算法初始誤差較大時，采用較大步進以加快迭代的收斂；而在算法后期估值逐漸趨于真值時，采用較小的步長以獲得盡可能小且穩定的迭代誤差。為此，通過研究Sigmoid 函數的曲線變化特性［8］，對函數進行平移和翻轉后，建立文中所提算法的變步長調整策略函數

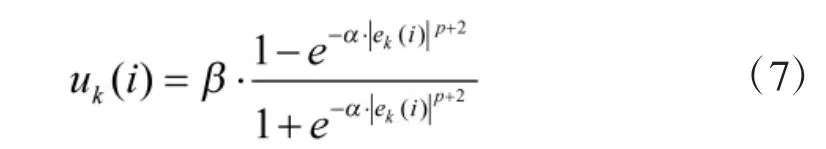
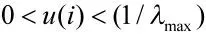
從圖2 所示曲線可以看出，隨著誤差項ek（i）的范數階數p 的增大，濾波誤差值在趨向于0 的過程，即濾波算法逐漸穩定的過程變得更加平緩，從而確保算法后期迭代步長的選擇更加合理。但范數階數p 值的過大賦值，算法中期u（i）值的變化生成的誤差項ek（i）的變化值會過小，易導致算法為確保合理的誤差項變化值而過于增大u（i）的變化步長，不利于算法對變步長值的合理設置，反而增加算法迭代過程的振蕩甚至無法收斂，而這一問題可以通過因子α 來彌補。從圖2 中|ek（i）|3曲線和0.5×|ek（i）|3曲線的變化特征可以看出，α 值的合理選擇增加了曲線杯口的寬度，使得u（i）曲線在保留p 值帶來的趨0 過程優勢的同時，增加算法中期步長變化與誤差變化的平衡。u（i）的步長變化可以生成合理的ek（i）值變化，從而有利于算法中期步長值的合理設置，加速算法的穩定收斂。綜上所述，通過合理設置估計值誤差ek（i）的范數階數p 和控制因子α，可以獲得平滑性較好的變步長u（i）隨估計值誤差ek（i）的變化曲線，滿足快速收斂和低穩態誤差的需要，而β 又可以確保變步長u（i）的初始極大值的合理設置。范數階數p 又增加了算法對脈沖噪聲等干擾的抗干擾性能［6］。

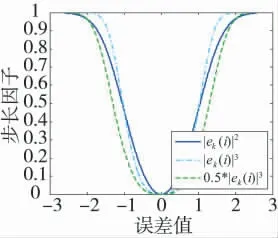
圖2 控制因子對步長影響

根據式（6）和式（7），基于估值約束和p 階范數約束的自適應最小均方濾波算法參數迭代公式可表示為：

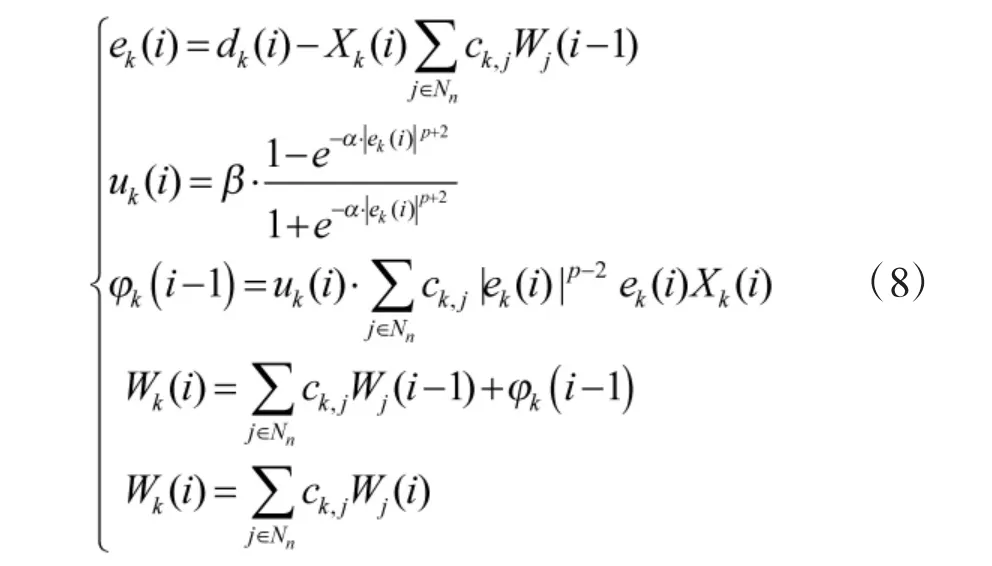
式中，相關參數與經典擴散LMS 算法一致，φk（i-1）為參數迭代計算的中間變量。

3 實驗分析

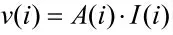
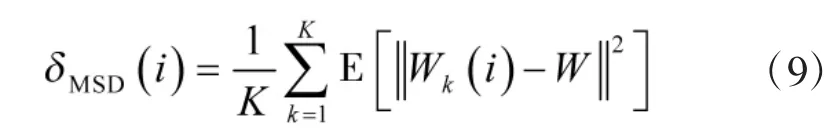
表1 文中算法的迭代計算流程

3.1 實驗設置

如圖3 所示為實驗使用的網絡連接圖，根據節點間的連接距離L≤0.3 判斷兩節點的通信互聯關系，并互為鄰居節點，pr=0.1，初始步長μ0=0.01。

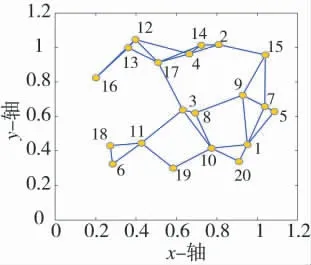
圖3 20 節點組成的分布式傳感器網絡

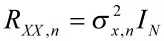
3.2 實驗結果分析

3.2.1 算法參數對算法性能影響

在改進算法中涉及α、β 和p 值3 個參數，α 和β 值控制變步長因子的波形，從而影響算法的收斂速度和穩態誤差；p 值影響算法的抗干擾能力和誤差趨0 過程的穩定性，需研究其值的設置對算法性能的影響規律。由于β 值控制步長因子的最大取值，其與p 和α 的取值之間影響不大，實驗中取β=0.02。而α 和p 之間，當調整p 值以適應不同的脈沖干擾噪聲時，其值同時影響到變步長因子u（i）曲線波形趨0 區域波形以及最大值到趨0 區域的波形陡峭程度（陡峭程度影響變化速率），而α 值可以改善波形的陡峭程序，為此實驗分析了α 和p 對算法的性能影響。采用圖3 所示傳感器網絡拓撲圖，當兩節點連接且距離時，認為兩節點存在通信互連，形成鄰域節點，每個節點疊加的脈沖噪聲，采樣點數為1 000，未知參數W 初始值從標準均勻分布U（0，1）中隨機抽取，實驗結果為20 次蒙特卡洛運算的平均值，如圖5 所示為算法在不同階數下進行參數估計的MSD 曲線。

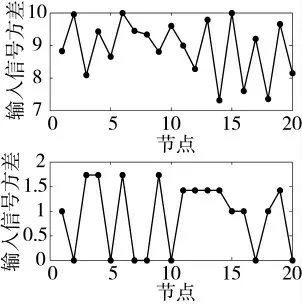
圖4 實驗中各節點輸入信號的方差

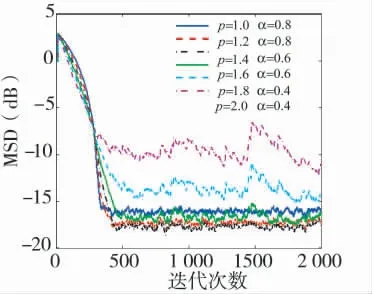
圖5 不同階數下參數估計的MSD 曲線

由于隨著階數p 值的增大，變步長會變得陡峭，需要α 控制因子隨之增大而逐漸減少，以緩解曲線的陡峭，因此，圖5 中α 取值隨p 值的增大而取較少值。從圖5 結果可以看出，當階數過高p=2或接近于2 時，即使α 取較少值緩解步長因子曲線的陡峭程度，算法仍無法達到穩定的收斂。而隨著階數p 的減少，算法可以收斂并獲得較好的穩態誤差，但并不是p 值越少越好。p 值較少算法收斂速較快，但變步長因子u（i）曲線波形在趨向于0 的區域不夠平緩，反而造成穩態誤差較大，如圖5 中綠色實線所示，而當p=1.4，α=0.6 算法在損失較小的收斂速度情況下，取得最小的穩態誤差，同時算法對脈沖干擾噪聲具有較強的抗干擾能力。

3.2.2 算法性能比較實驗

如圖4 所示為性能比較實驗中分布式傳感器網絡各個節點的輸入信號方差和輸入噪聲方差，符號DLMS 算法參數δ=0.2，文中算法參數α=0.6，p=1.4，圖6 所示為4 種算法進行參數估計實驗得到的MSD 曲線。

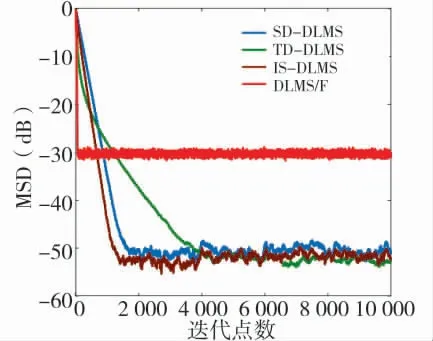
圖6 實驗中各算法的估計性能MSD 曲線

從圖6 可以看出，DLMS/F 算法相比于其他3種算法具有明顯的收斂速度優勢，但其收斂穩態誤差也遠高于另3 種算法。在算法性能方面，所提算法與符號DLMS 的穩態誤差和收斂速度性能相近，但所提算法收斂速度略有優勢，且穩態誤差更小。而與傳統DLMS 算法的參數估計性能相比，在保持相近的最終穩態誤差基礎上，所提算法具有更快的收斂速率，在達到相近穩態誤差時，具有明顯的時間優勢，說明所提算法取得較好的參數估計性能。

總體分析實驗結果，所提算法取得較好的參數估計效果，主要因為合理的變步長控制因子設置保證了初期較大的步長加快收斂，后期較小步長緩解迭代振蕩，以得到較小的穩態誤差，同時算法較小的穩態誤差也進一步驗證了算法較強的抗噪能力。

實驗又設計了3 組不同拓撲結構和節點數的分布式傳感器網絡，并分別進行性能比較實驗，4 種算法的20 次重復實驗參數估計誤差的統計均值如表2 所示，比較表中各算法誤差值可以看出，文中算法的穩態誤差更小，且大幅提高了算法的收斂速度，對脈沖噪聲有較好的魯棒性。

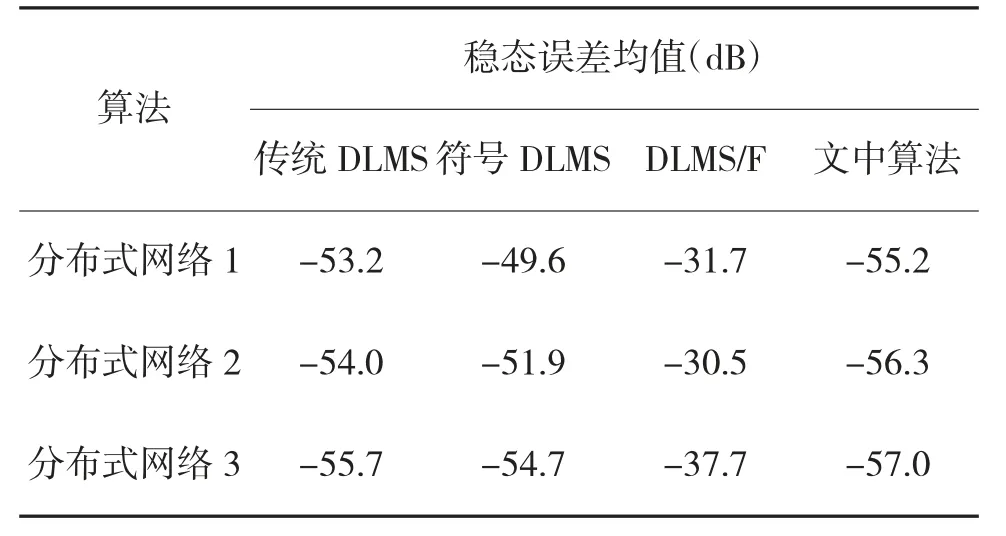
表2 3 組實驗中各算法的誤差平均值

4 結論

在進行分布式無線傳感器網絡的未知參數估計時，為了使自適應波濾算法具備快速收斂和低穩態誤差，同時可處理脈沖噪聲的干擾，文中設計了一種基于估計約束的分布式網絡最小均方算法。在算法中通過使用參數估值的p 階范數增強算法的抗脈沖噪聲干擾能力，通過變步長控制函數，使得算法迭代時的步長因子能夠在算法初期以較大變步長加快收斂速度，而在算法后期以緩慢的變步長變化獲得較低的穩態誤差，多組實驗結果表明，相比已有算法，所提算法的參數估計性能更優。

但是針對脈沖噪聲干擾，需要在大量實測噪聲實驗基礎上，進一步合理設置算法中α、β 和p 值參數值，以增加算法的魯棒性和自適應能力。