基于證據理論的Bow-tie 航空風險評估方法及應用*

徐吉輝，王曉琳，王 瑛，章 磊，陳玉金

（空軍工程大學裝備管理與無人機工程學院，西安 710051）

0 引言

安全是航空業永恒的主題，航空活動往往伴隨著高風險、高隱患、事故后果嚴重等特點，為有效緩解與控制安全風險，航空風險分析工作備受關注［1-3］。

近年來，針對航空風險分析進行了廣泛的研究，王永剛［4］等在事故樹分析法（FTA）的基礎上結合貝葉斯網絡（BN）建立風險模型；Cui［5］在安全性指標的基礎上，提出一種基于不確定性的安全性功能函數，結合Bow-tie 模型進行給定嚴酷度條件下的風險評估；李巖［6］等提出一種基于Kriging 和蒙特卡羅半徑外重要抽樣混合的結構概率風險評估方法；施志堅［7］等引入多元聯系數集對分析理論進行航空維修風險態勢評估。相較于其他安全風險分析方法，Bow-tie 分析是一種能夠全面整合定性與定量信息、聯系事因和后果的系統性風險分析方法。目前關于航空風險的Bow-tie 分析應用主要集中于定性分析。孫殿閣等［8］利用Bow-tie 模型對民用機場的日常運行安全風險進行了分析；高揚［9］等在Bow-tie 模型量化中引入結構重要度，識別需要重點控制的基本事件。

然而，實際航空活動中存在的大量認知不確定會導致理論分析與實踐結果存在明顯差異，解決不確定條件下的航空風險評估定量化分析不足越來越成為研究的重點與難點。按照不確定性的來源及其對不確定性認知水平的不同，不確定性分為隨機不確定性（Aleatory uncertainty） 和認知不確定性（Epistemic uncertainty）兩大類，隨機不確定性為系統固有屬性，難以處理或消除［10-11］。針對認知不確定性，模糊理論、證據理論、云模型等都是有效的解決手段。Faisal 等［12］利用模糊理論解決Bow-tie 分析中的不確定性，從而實現對風險的定量評價；Refaul 等［13］提出了基于證據理論的Bow-tie 分析方法，比較而言，證據理論對認知不確定性的處理更具優勢，能夠直接表達“不確定”的信息和“不知道”的信息。

因此，為充分利用專家信息，解決Bow-tie 模型對航空風險進行評估過程中存在大量認知不確定性的問題，本文考慮引入D-S 證據理論，一方面有效處理了Bow-tie 分析中數據及模型不確定性，另一方面通過靈敏度分析，得到危害度較大的關鍵事件，最后，結合某型航空器輪胎爆破事故進行實例分析，驗證了本文方法的有效性。

1 Bow-tie 方法

Bow-tie 分析法（Bow-tie Analysis）是由事故樹分析（FTA）和事件樹分析（ETA）通過頂事件結合產生的，能夠直觀地顯示出潛在危險源與后果事件的內在聯系，主要用于識別危險源、評估及控制風險等［14］。

圖1 所示為Bow-tie 模型的結構示意圖，包括基本事件（BE）、中間事件（IE）、邏輯門、頂事件（CE）、控制事件（E）和結果事件（OE）等元素。其中，基本事件為可能導致事故發生的危險源，頂事件為事故本身，控制事件為緩解和補救措施，結果事件則為事故可能會造成的一系列后果［15-16］。

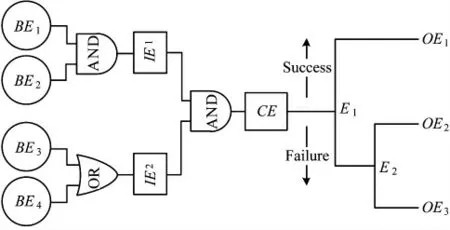
圖1 Bow-tie 模型示意圖

在進行Bow-tie 模型定量化分析時，以基本事件和控制事件的發生概率作為輸入變量，通過相應路徑的邏輯運算計算得到輸出變量，即頂事件的發生概率以及結果事件的發生概率。由于確定的輸出事件能夠限定其嚴重程度，因此，可以用該事件發生的可能性描述其風險水平，進一步地，表示評價對象或活動的安全性。

2 證據理論

D-S 證據理論是Dempster 和Shafer 提出的描述認知不確定性的重要理論，利用上下概率（即信任函數與似然函數）代替精確概率值來描述研究變量的不確定性［17-19］。

信任函數與似真函數構成的信度區間［Bel（A），Pl（A）］用于描述變量發生可能性的取值范圍。當存在多個證據時，就需要進行證據合成計算，Sentz 總結了證據理論合并規則，并指出Dempster 合成規則是最為應用廣泛規則［17］：

設m1，m2為可獲取的獨立證據，則

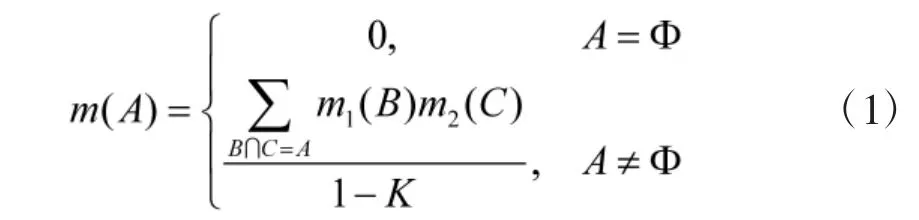
3 基于證據理論的Bow-tie 分析流程

3.1 構造基于證據理論的Bow-tie 模型

Bow-tie 模型定量化分析過程中存在大量的不確定問題，如由于樣本量不足或數據缺失所導致的數據不確定性問題，或由于同一類元素之間相互依賴影響在模型中無法體現所導致的模型不確定性問題。本文利用D-S 證據理論來解決此類不確定問題，具體的模型構造及證據理論的應用如圖2 所示。

圖2 引入證據理論的Bow-tie 模型分析流程

3.2 建立辨識框架

Bow-tie 分析中，不確定信息主要來源于基本事件BE、控制事件E 及節點依賴系數，利用D-S 證據理論處理事件及節點依賴程度的不確定性時，首先要針對不確定參數建立辨識框架，在此基礎上收集專家證據。

1）對事件變量（BE 和E 發生概率P）進行的證據描述主要針對的是數據不確定性問題。一般而言，在Bow-tie 模型中，基本事件的狀態對應“發生”或“不發生”，控制事件則具有“成功”或“失敗”雙重分支，因此，事件辨識框架可以定義為Θ{S，F}，對應冪集P 為{Φ，{S}，{F}，{S，F}}。

2）對節點變量（依賴系數Cd）進行證據描述主要針對的是模型不確定性問題。Refaul［13］認為節點所連接的事件之間存在相互影響，提出了依賴系數描述這種影響程度的大小。基于此，本文結合相關度9 級評語，論域由1～9 分別為非常低、很低、低、較低、中等、較高、高、很高、非常高，將節點依賴系數的辨識框架定義為Θ{1，2，3，4，5，6，7，8，9}。

3.3 確定基本概率賦值

假定專家意見相互獨立，依據相應的辨識框架，通過德爾菲法獲取專家評語，根據經驗對Bow-tie 分析中涉及的輸入變量的各種情況作出判斷，其判斷結果用概率表示，即為冪集P 中情況的基本概率賦值。對于事件變量而言，冪集P{Φ，{S}，{F}，{S，F}}為全部假設；對于節點變量而言，全部假設為{{1}，{2}，{3}，{4}，{5}，{6}，{7}，{8}，{9}，{Θ}}。基本概率賦值（BPA，Basic Probability Assignment）表示專家對某一假設發生的信任程度，也可以認為是證據對該假設下輸入變量發生可能性的支持度。

3.4 合成專家證據

對于兩個或多個專家提供的證據，通常需要利用合成規則，計算出一個mass 函數。通常采用Dempster 合成規則，但當證據存在高度沖突時，Dempster 合成規則得到的組合結果可能存在悖論，本文引進Yager 合成規則計算存在融合悖論時的組合mass 函數：

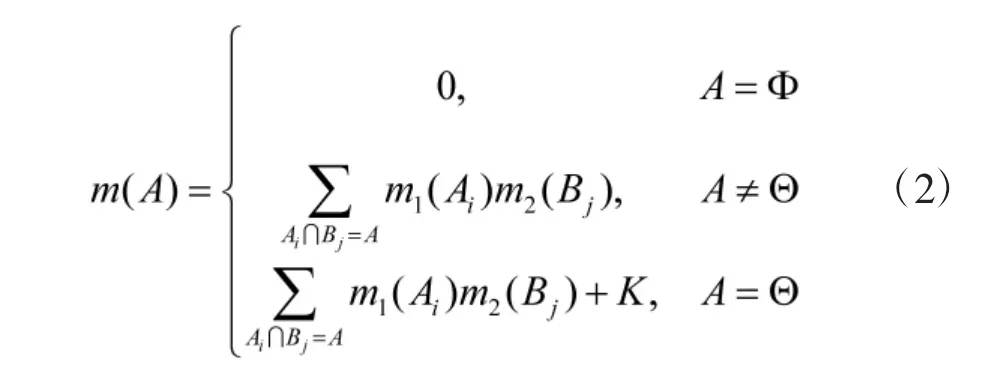
3.5 計算輸入變量的信度區間

在合成得到mass 函數后，需要依據事件及節點依賴系數，計算相應的信度區間。信度區間表示對某一假設的支持力度，區間下限為信任函數Bel（A），區間上限為似真函數Pl（A）。

1）事件變量信度區間的計算主要是依據定義法，根據式（1）計算得到。對于基本事件BE 關注其發生故障（S 假設）的信度區間，對于控制事件則關注其措施失效（F 假設）的信度區間。

2）對于節點變量信度區間的計算，一方面與節點變量本身的專家證據有關，另一方面與假設情況的固有取值區間有關，其計算公式如下：

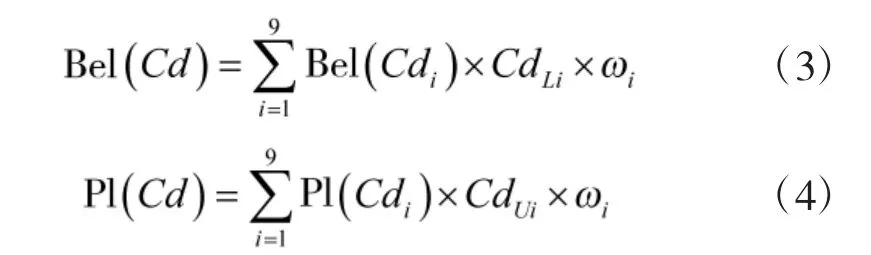
3.6 計算輸出變量的信度區間

在FTA 中，以基本事件發生概率和節點依賴系數的信度空間為基礎輸入變量，結合不同的邏輯門算法傳導至頂事件；在ETA 中，以控制事件概率和節點依賴系數的信度空間為基礎輸入變量，按照生效或失效路徑傳導至結果事件。表1 所示為計算頂事件和結果事件的發生概率的信度區間的公式。

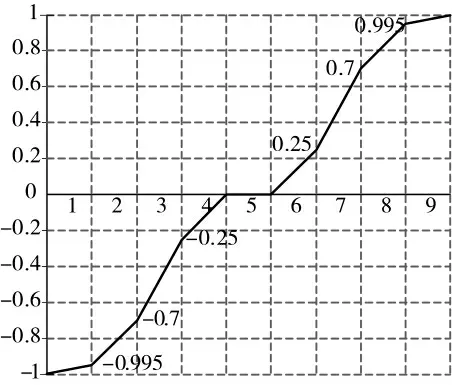
圖3 依賴程度評語等級的上下限

表1 輸出變量發生概率信度區間的計算公式

3.7 確定精確取值

計算得到輸出變量的信度區間后，需要進一步精確化處理，得到描述其發生可能性大小的取值，直觀地表示出輸出事件的風險水平，其估算公式如下：

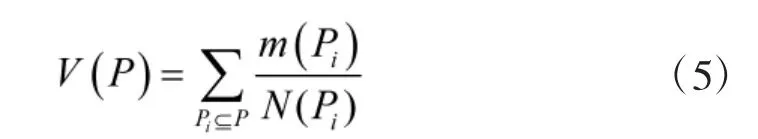
其中，N（Pi）為假設Pi中所包含的元素個數。

3.8 靈敏度分析

對Bow-tie 模型進行靈敏度分析的主要作用是可以評估各基本事件對頂事件的影響程度差異，查找導致事故發生的基本事件中的系統薄弱環節，從而制定針對性的安全水平提升措施。

首先，分別計算基本事件對不同后果事件的Birnbaum 重要度：

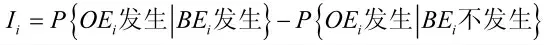
根據重要度數值對輸入事件進行排序，對不同后果事件得到的重要度排序進行綜合排序，從而更加合理地識別得到重要度大的輸入事件即為需要關鍵事件。

4 案例分析

輪胎是航空器起落系統中的重要部件，對于飛機正常起降活動產生至關重要的作用，一旦故障可能會導致嚴重的后果。本文以某型航空器輪胎爆破事故為例，分析導致事故發生的原因及其后果事件，并對故障實施控制措施，具體分析過程如下。

4.1 構建輪胎爆破事故的Bow-tie 模型

對輪胎爆破事故進行Bow-tie 分析要以模型為基礎，因此，通過識別事件元素、節點元素，分析事故原因及發展路徑，構建事故Bow-tie 模型如下頁圖4 所示，底層故障模式為基本事件，頂事件CE 為輪胎爆破，控制事件E1為啟動應急剎車系統、E2為避讓飛機及建筑物、E3為增設隔離網、E4為啟動應急消防措施，結果事件OE1為停留在跑道、OE2為機體輕度損傷、OE3為機體嚴重損傷、OE4為飛機起火且人員傷亡，N-1 至N-15 為節點。

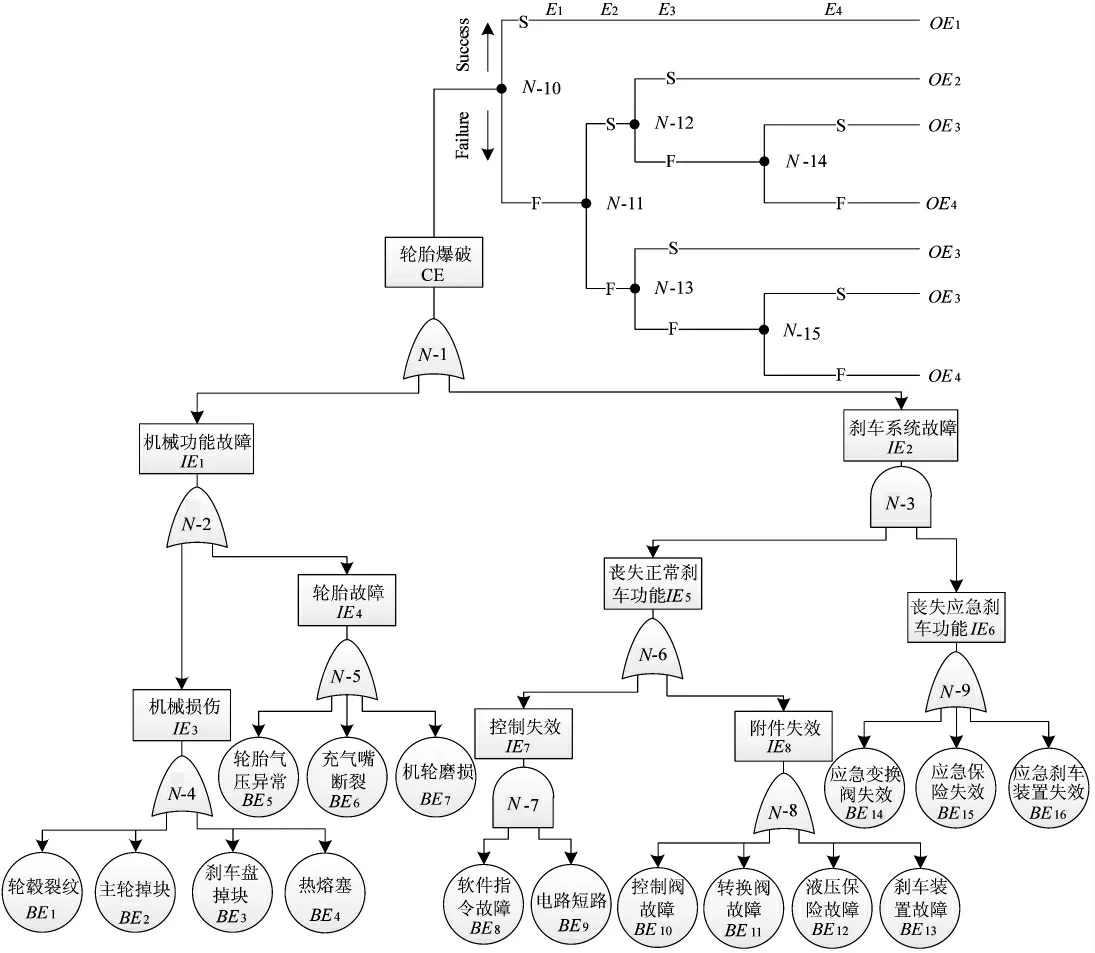
圖4 輪胎爆破事故的Bow-tie 模型

4.2 計算輸入變量發生概率的信度區間

由兩位相互獨立的專家分別對輸入變量提供證據，節點依賴系數的證據見表2，基本事件和控制事件的發生概率的證據見下頁表3，根據Dempster合成規則進行計算，表4 為輸入變量經過證據合成后的結果。

4.3 計算輸出變量發生概率的精確描述值

根據輸入變量合成后的信度區間，根據表1 中給出的公式計算輸出變量發生概率的信度區間，結果見表5。

對輸出變量的信度區間進行解模糊化處理，得到相對精確的描述值：

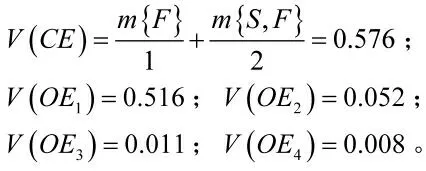
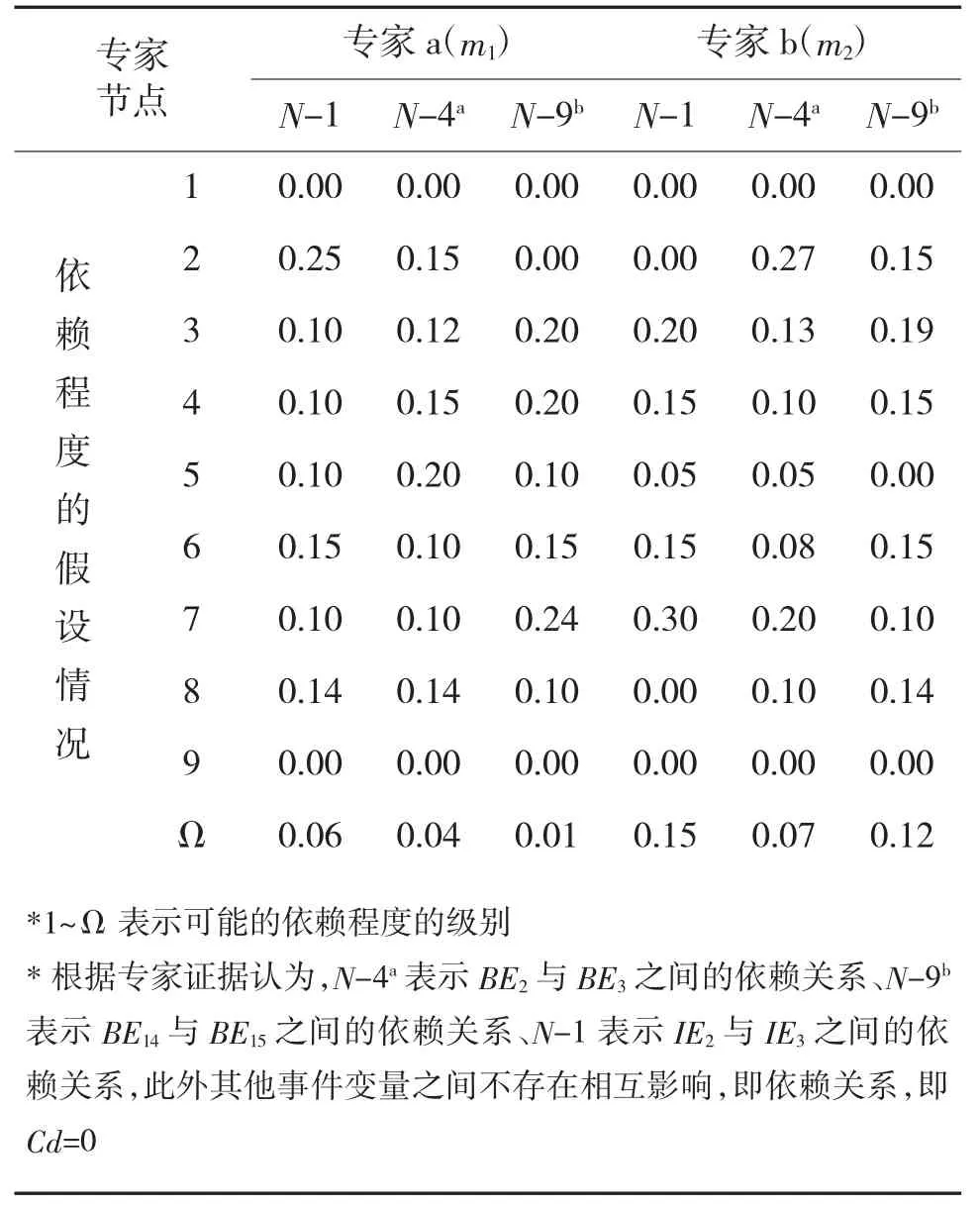
表2 輸入節點變量的專家證據

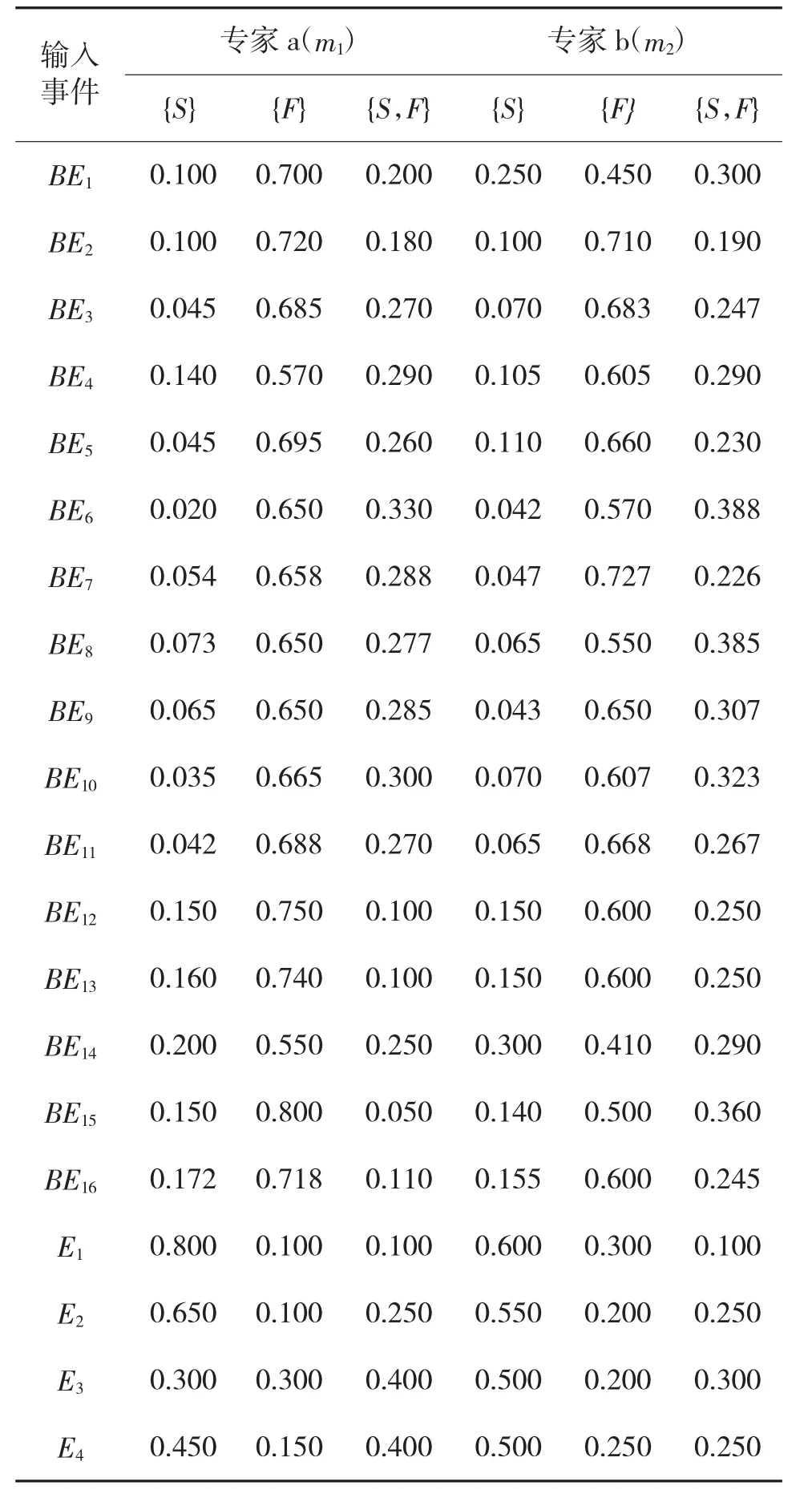
表3 輸入事件變量的專家證據

4.4 靈敏度分析

分別以OE1、OE2、OE3和OE4為輸出變量，計算輸入事件的重要度，具體排序結果及綜合重要度見下頁表6。

根據表6 中計算結果可知，對于不同的后果事件所需要重點關注的基本事件略有差異，通過加權平均后得到的綜合重要度在一定程度上能夠代表基本事件的排序。因此，本例中得到，需要在工作過程中重點關注的基本事件為BE1、BE4、BE6，在工程實踐中應采取相應的措施對其所對應的危險源進行控制。

5 結論

本文利用證據理論處理航空風險Bow-tie 分析中的認知不確定問題，一方面Bow-tie 分析圖能夠清晰表示事故的原因與后果，另一方面定量化分析又能有效地計算事故及其引起的后果發生的可能性，具有較強的實際應用價值。

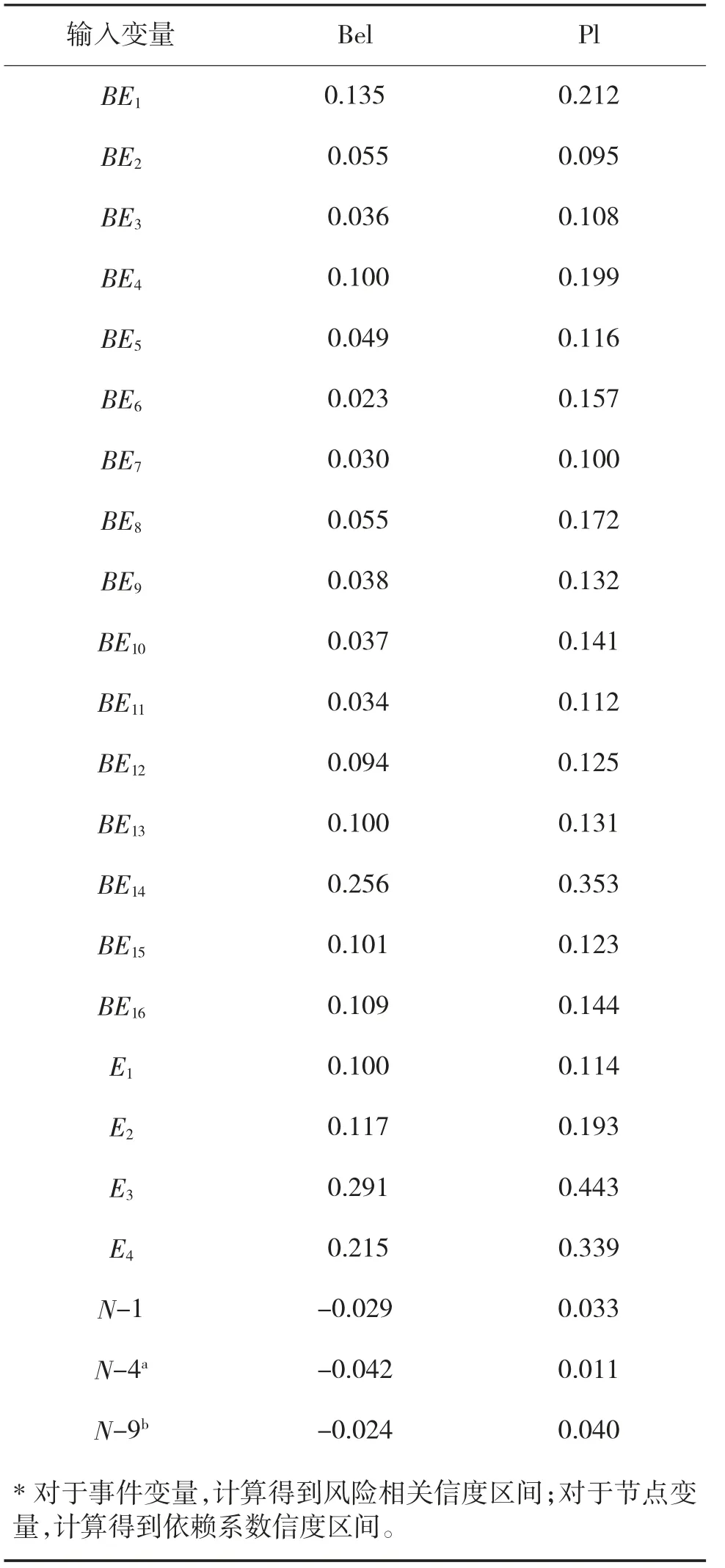
表4 證據合成后輸入變量的信度區間

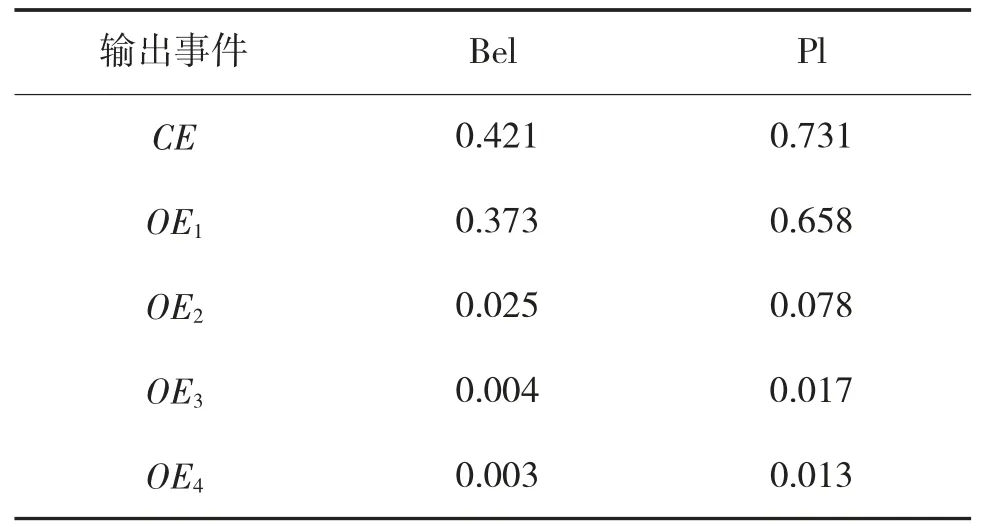
表5 輸出變量發生概率的信度區間

1）引入證據理論的Bow-tie 分析能夠有效解決當前航空風險評估工作中量化難、專家信息利用率不高的問題。

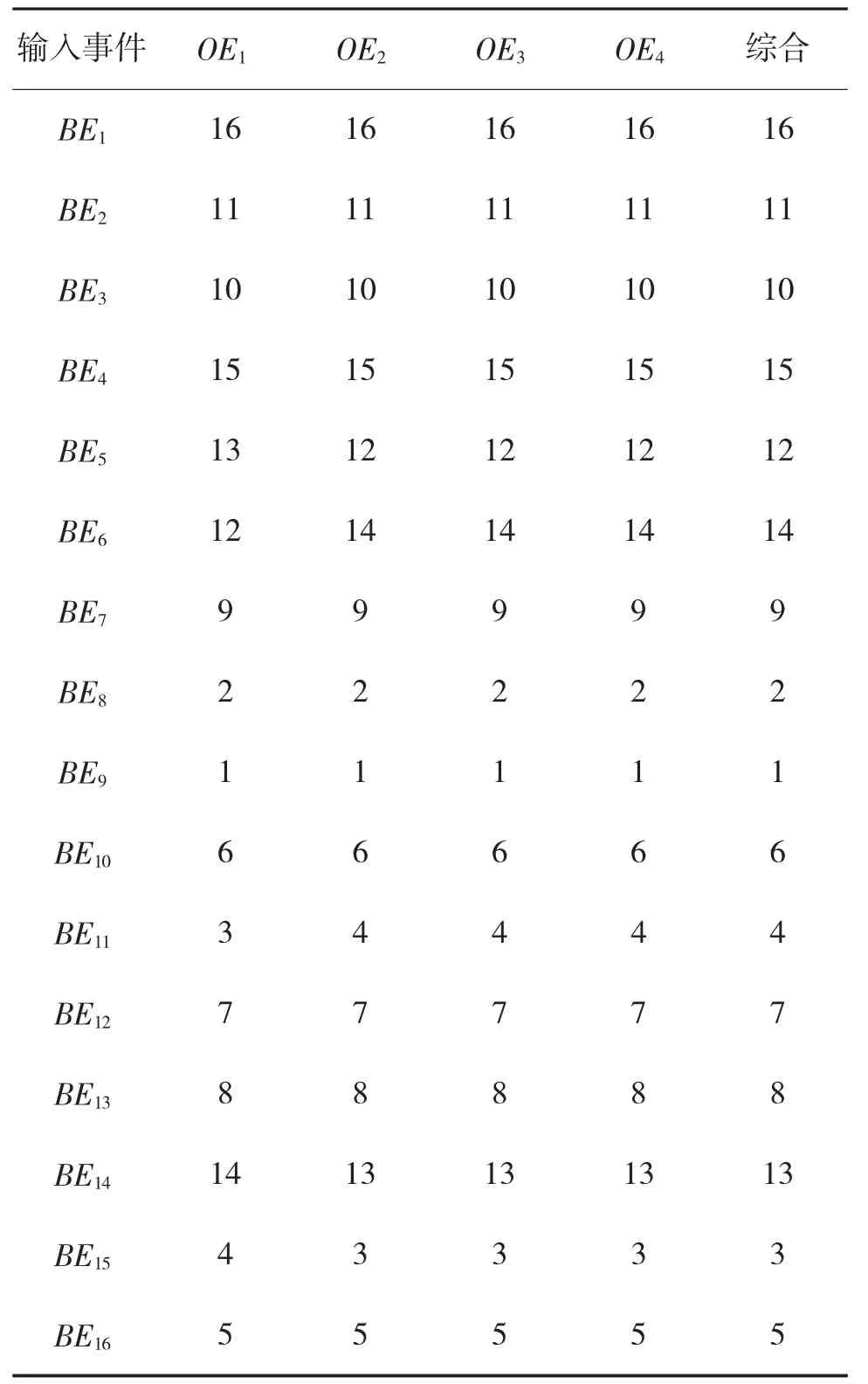
表6 靈敏度分析結果

2）專家經驗解決了量化過程中由于數據缺失所導致的數據不確定性問題，節點依賴系數的引入則解決了模型變量間影響的不確定問題。

3）通過基于Birnbaum 重要度的靈敏度分析，確定了實際工程中需要重點關注的關鍵事件。

4）通過輪胎爆破事故實例，驗證了本文方法的可行性，同時，靈敏度分析得到對后果事件影響較大的事故原因，為安全性指標的預計與分配、預防措施和控制措施的制定提供了決策依據。