數字濾波對擾動基座初始對準影響分析*
阮 娟,梅春波,譚 磊
(西安現代控制技術研究所, 西安 710065)
0 引言
捷聯慣導初始對準按對準過程可以分為粗對準和精對準[1-2]。粗對準為后續精對準過程提供粗略的姿態初始值。針對基座存在大幅晃動干擾的情況,文獻[3]提出了一種巧妙的慣性系粗對準算法。該算法能夠隔離基座的晃動對粗對準過程的影響,解決了大幅角運動情況下的粗對準問題。
在實際的大幅度角運動對準環境中,慣導系統除了會受到角運動干擾外,還會受到線運動的干擾,如發動機的振動、陣風等干擾。為了降低各種線運動干擾對初始對準的影響,各種數據預處理算法被應用到初始對準中,如FIR數字濾波算法[4]、最小二乘濾波[5]、多尺度小波濾波算法[6]、提升框架小波濾波[7]及IIR低通濾波算法[8]等。
文中在上述工作的基礎上,基于抗擾動初始對準原理,采用FIR數字低通濾波器來做數據預處理,然后利用慣性系粗對準算法完成晃動基座下的粗對準過程,利用Kalman濾波算法實現精對準。其次,利用實驗室慣導系統模擬擾動環境,設計驗證試驗,驗證所設計算法的有效性。最后,給出驗證結果及相關結論。
1 抗擾動初始對準算法設計
抗擾動初始對準算法由三部分組成:第一部分是處理對準過程中的角晃動干擾,通過引入慣性系,進行姿態陣分解和姿態跟蹤算法解決;第二部分是處理對準過程中的線加速度干擾,通過引入線性FIR濾波預處理算法解決;第三部分是在慣性系內設計的卡爾曼濾波精對準算法,完成精對準。
1.1 角晃動干擾隔離原理
對姿態陣進行鏈式分解,即
(1)
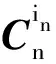
(2)
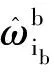
1.2 線加速度干擾的預處理
在前文定義的慣性系內,依據牛頓第二定律,可以得到慣性系比力方程為
(3)
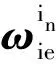
晃動基座條件下,式(3)等號右端前兩項分別為基座晃動所產生的干擾加速度和干擾哥氏加速度。雖然存在干擾速度,但是基座的平均位置并未改變,因此,干擾加速度和干擾速度均可視為高頻小幅值周期函數。將式(3)等號右端前兩項合稱為干擾加速度,記為ar(t),則有
fin(t)=-gin(t)+ar(t)
(4)
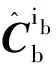
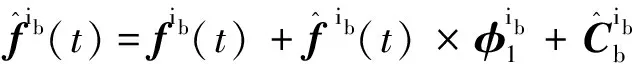
(5)
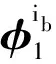
將式(4)代入式(5)中,則有
(6)
等式右端第一項為重力加速度和加速度計測量誤差之和,二者在頻域內有重疊,不可分離,為低頻分量;第二項為周期性干擾加速度項,為高頻分量。
針對式(6),可以在頻域內設計數字低通濾波算法,抑制其中的干擾加速度。不同的應用背景,干擾加速度的頻率范圍不同,所使用的低通濾波手段也有所差別。
文中設計具有線性相位的FIR數字低通濾波器來對干擾加速度進行處理,濾波器系數滿足:h(n)=h(N-1-n),即h(n)為偶對稱,N取為奇數。該濾波器具有線性相位,通帶內的數據經過該濾波器后,僅僅是在時間上有延遲,幅度和形狀保持不變,延遲量為(N-1)/2拍,延遲拍數乘以采樣周期即是對應的延遲時間。
設計低通濾波器時,需要了解實際對準環境中基座擾動的頻率范圍,主要指線運動的頻率范圍。文獻[9]通過對實際的車載環境下數據的分析得出,車載條件下,由于受到發動機振動影響或人為干擾而導致的擾動加速度的頻率均在0.5 Hz以上。文獻[3]則指出艦載環境中擾動加速度的頻率均在1/15 Hz以上。在實際應用中,以此為選擇標準,就可以完成對低通濾波器的設計。
(7)
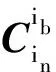
(8)

1.3 慣性系卡爾曼濾波精對準
在慣性系精對準過程中,利用陀螺儀輸出進行載體系姿態跟蹤,考慮器件誤差,則有
(9)
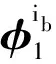
考慮器件誤差時,載體系比力積分模型為
(10)
由此,可建立慣性系線性卡爾曼濾波精對準方程如下:
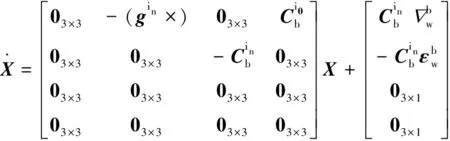
(11)
2 試驗驗證
2.1 驗證方案設計
數據采集時序圖如圖1所示。
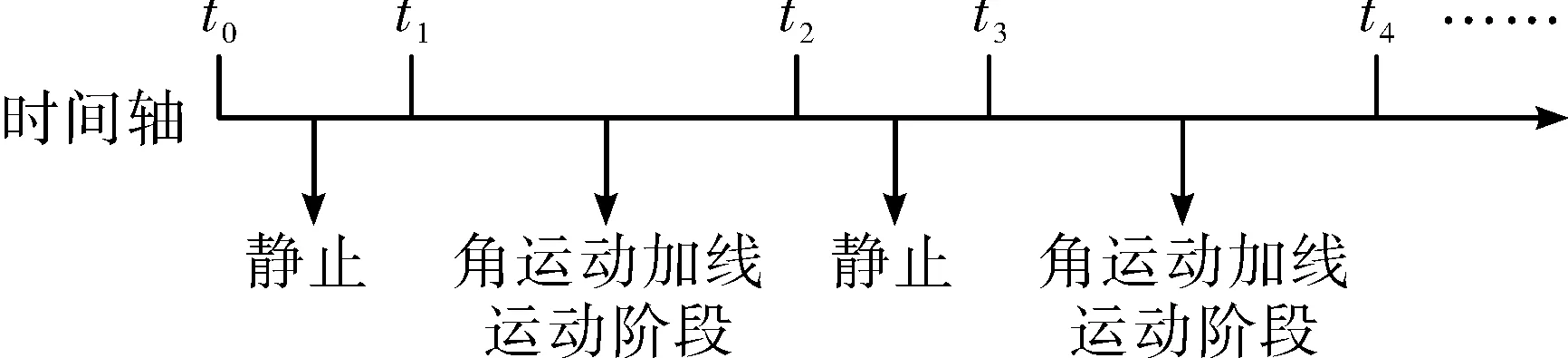
圖1 驗證試驗時序圖
在圖1中,利用靜止階段數據完成捷聯慣導系統的靜基座初始對準,獲取t1時刻的姿態初值。從t1時刻開始進行捷聯姿態更新,以捷聯姿態更新的結果作為實時的姿態真值。然后,利用t1至t2時間段內的數據完成基于重力信息的初始對準,并用參考姿態來評估對準的效果。
驗證試驗在實驗室內進行,試驗采用的慣導設備為激光捷聯慣導系統。陀螺漂移重復性誤差為0.008°/h,加速度計零位穩定性≤4.0×10-5g,數據更新周期為10 ms。驗證試驗共進行了3組,兩組在試驗車上進行,車上第一組施加小幅度的角晃動和線運動干擾;車上第二組施加了稍大幅度的角晃動和線運動干擾;第三組利用人力操作慣導系統模擬惡劣的大幅角晃動干擾和線運動干擾。
2.2 試驗結果
第一組微幅晃動試驗結果如圖2~圖5所示。
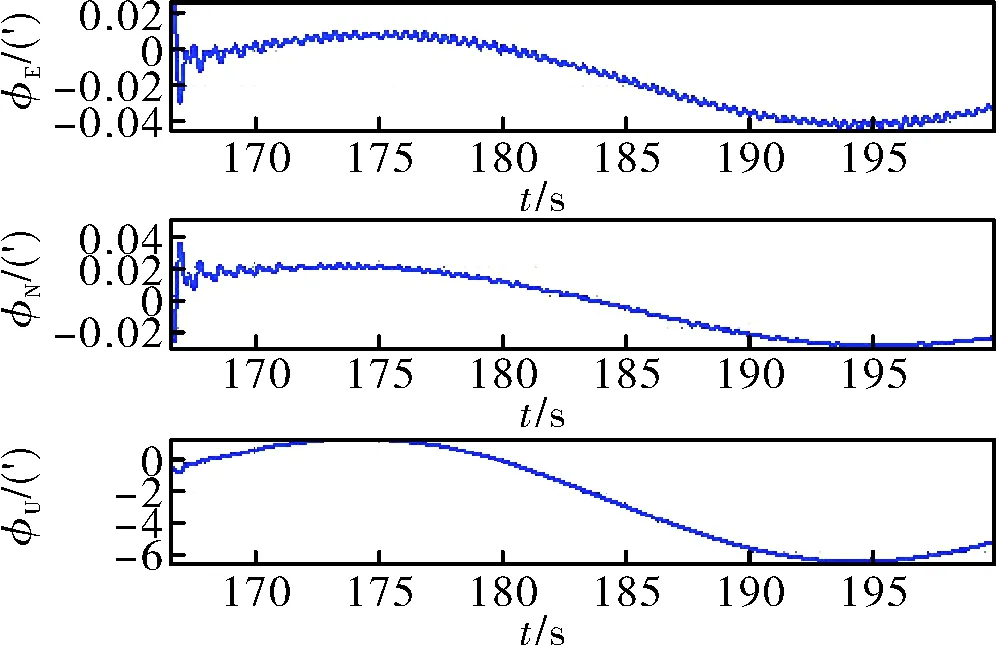
圖2 經過數字濾波預處理后粗對準誤差
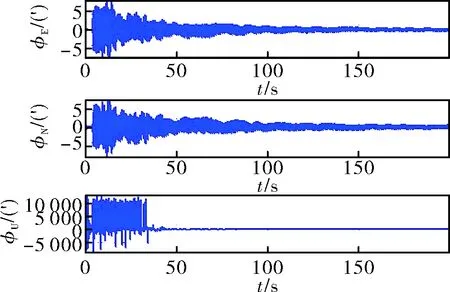
圖3 未經數據預處理粗對準誤差
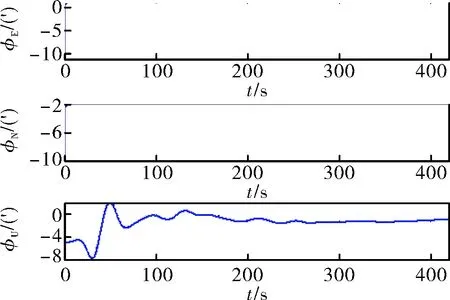
圖4 經過數字濾波預處理后精對準誤差
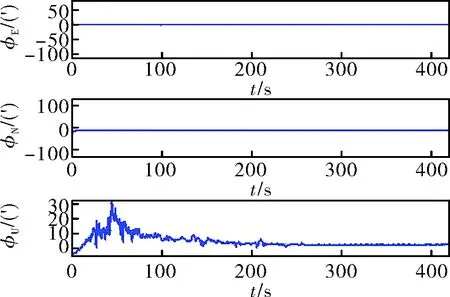
圖5 未經數據預處理精對準誤差
第二組晃動試驗結果如圖6~圖9所示。
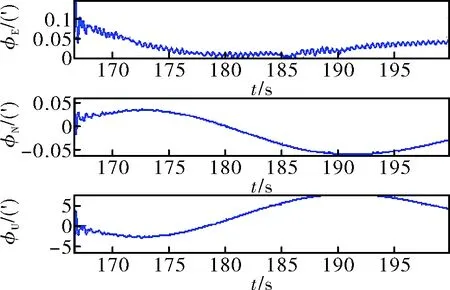
圖6 經過數字濾波預處理后粗對準誤差
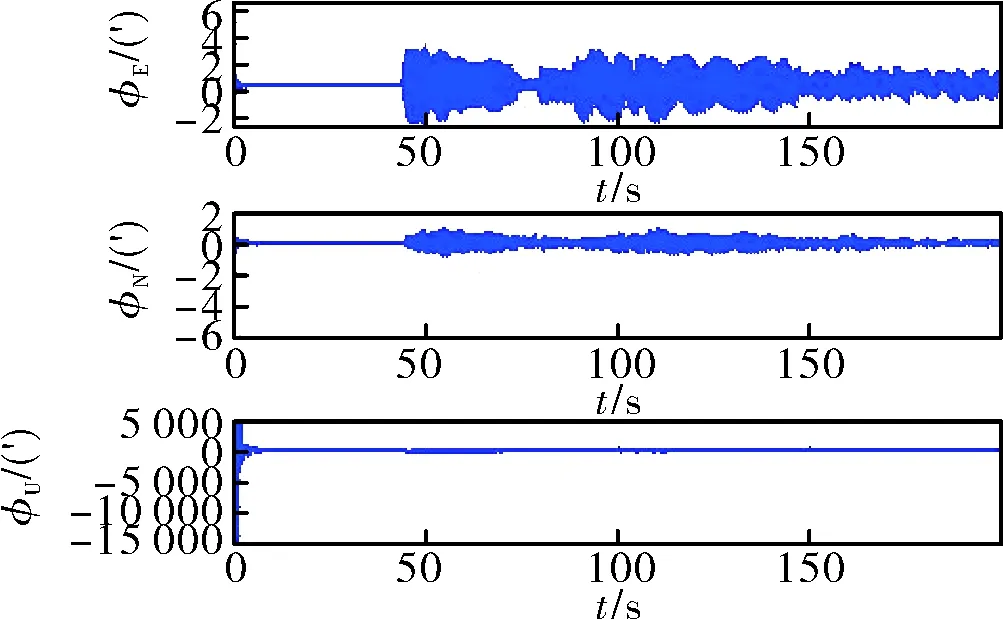
圖7 未經數據預處理粗對準誤差
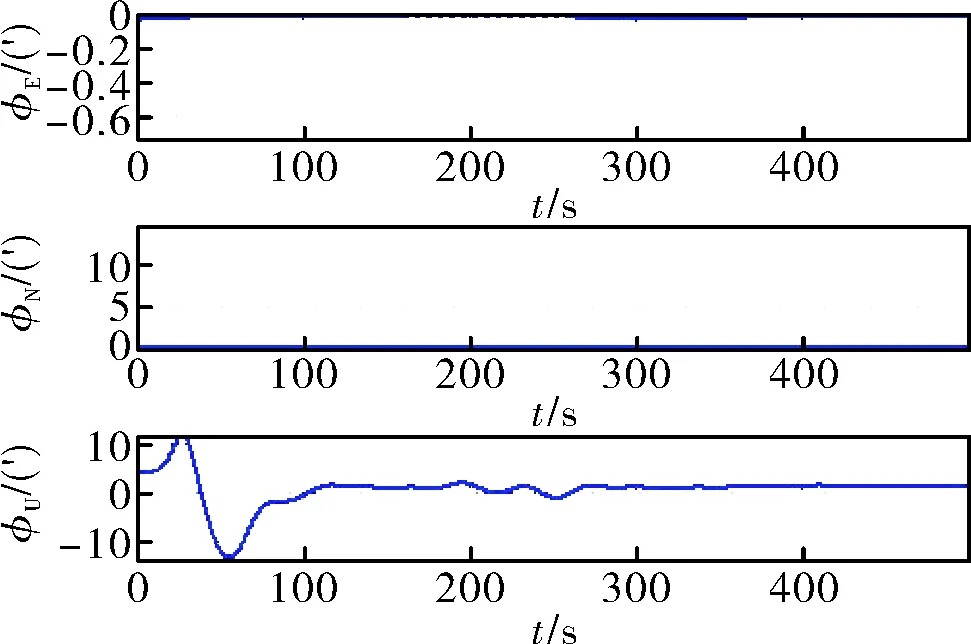
圖8 經過數字濾波預處理后精對準誤差
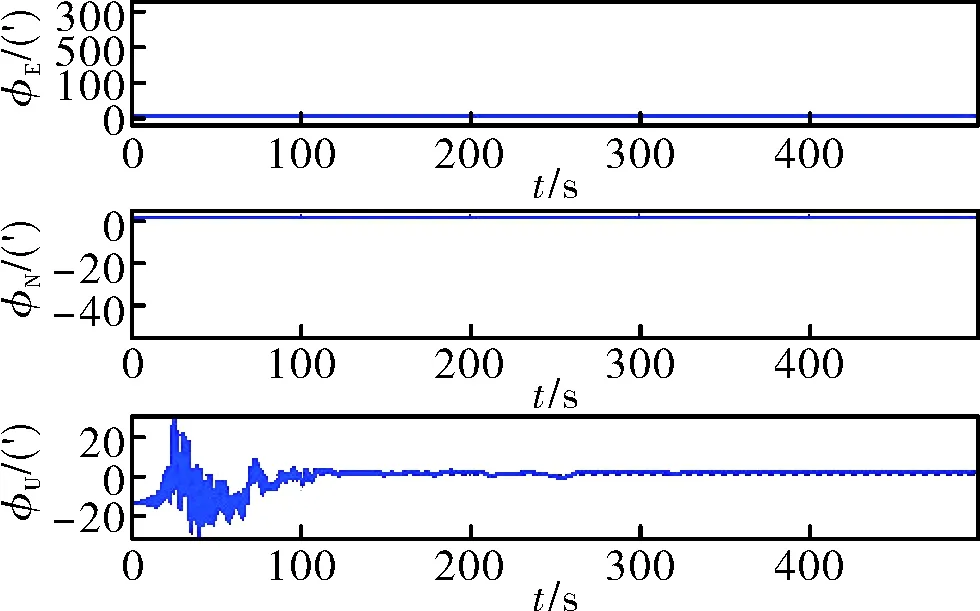
圖9 未經數據預處理精對準誤差
第三組惡劣晃動試驗結果如圖10~圖14所示。
其中,φU、φN、φE分別為天、北、東方向的對準姿態誤差,φ、γ、θ分別為航向角、滾轉角和俯仰角。
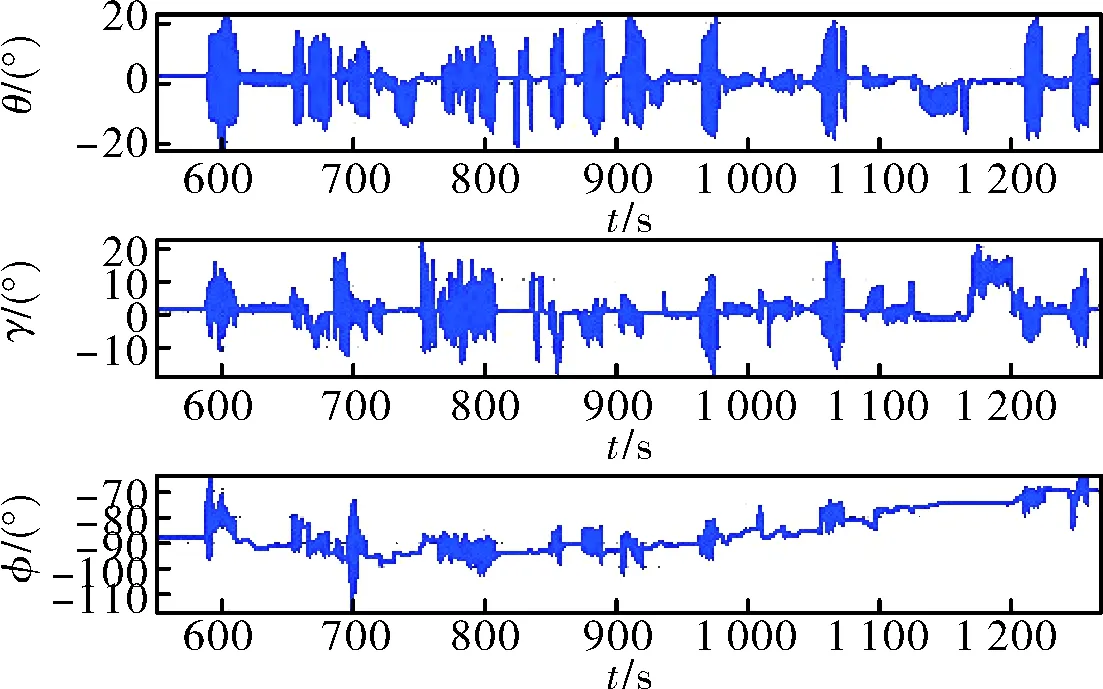
圖10 第三組惡劣晃動條件下的慣組姿態變化
2.3 試驗結論
根據3組驗證試驗,可以得到如下結論:
1)FIR數字濾波器能有效地抑制噪聲及未知線運動干擾,提高粗對準的收斂速度和收斂精度。
2)FIR數字濾波器對精對準的結果影響較小,經過濾波處理后精對準的結果更加平滑,但是精對準的精度基本保持不變。
3)3種試驗條件下,所設計的初始對準算法均可在5 min內達到與靜基座初始對準相同的精度。
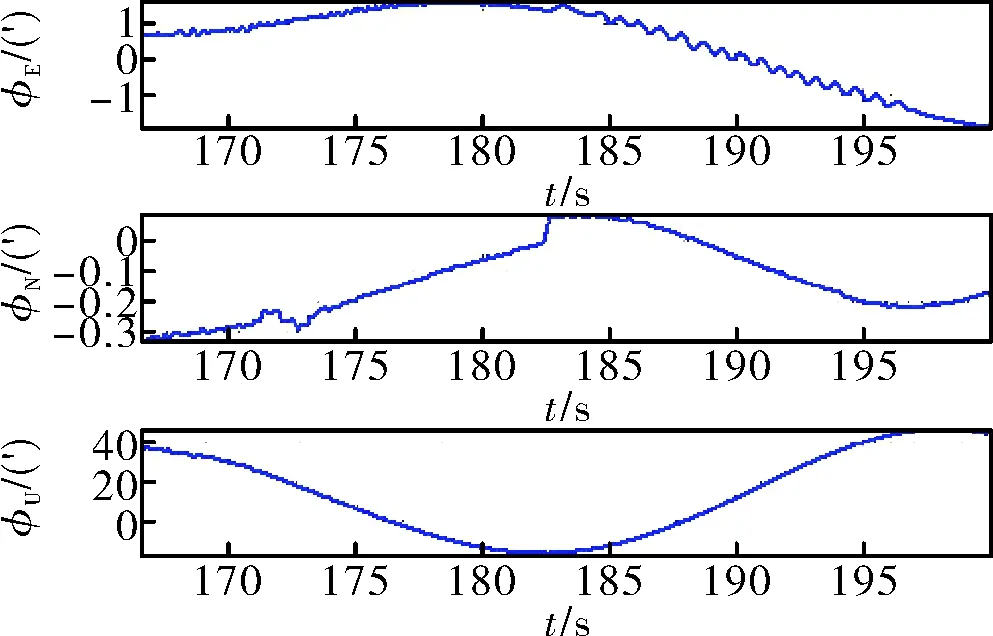
圖11 經過數字濾波預處理后粗對準誤差
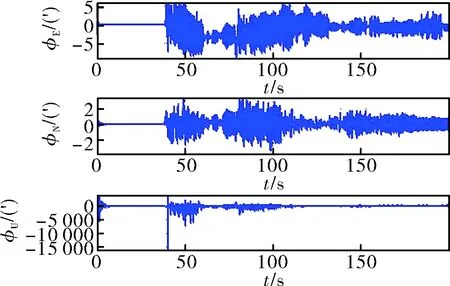
圖12 未經數據預處理粗對準誤差
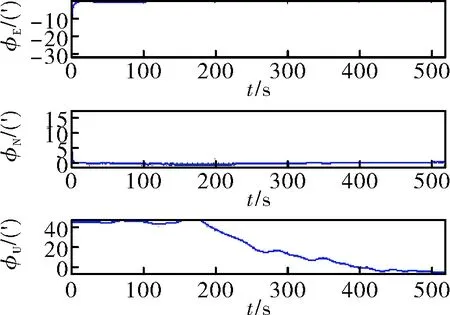
圖13 經過數字濾波預處理后精對準誤差
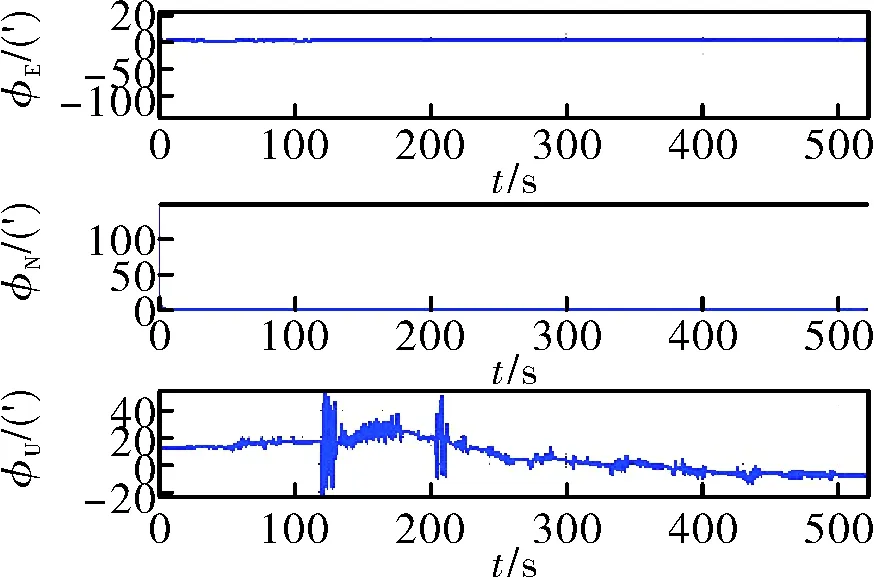
圖14 未經數據預處理精對準誤差
3 結論
通過文中的分析和試驗驗證結果,可以發現,通過引入低通數字濾波對慣導數據進行預處理,可以實現對粗對準過程中載體線運動干擾的抑制,從而改善慣性系粗對準算法的收斂效果和收斂速度,同時對精對準的估計結果有一定的平滑作用。

