局部模型回歸分析

胡良平

（1.軍事科學院研究生院，北京 100850；2.世界中醫藥學會聯合會臨床科研統計學專業委員會，北京 100029 *通信作者：胡良平，E-mail：lphu812＠sina.com）

1 概 述［1］

1.1 局部回歸模型

局部回歸模型見式（1）：

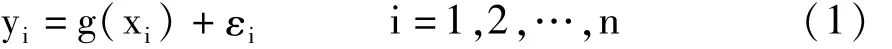
在式（1）中，yi為第i次觀測到的因變量的取值；g（xi）是 xi的回歸函數；xi可以是一個自變量，也可以是由多個自變量組成的向量；εi是一個隨機誤差。

1.2 局部模型回歸分析應用的場合

一般來說，在因變量服從正態分布或對稱分布時，欲研究因變量隨自變量變化而變化的依賴關系時，可以嘗試采用很多種方法來創建回歸模型，包括采用“局部回歸模型”。最適合運用此模型的場合如下：在自變量的全部取值范圍內，存在多個“小區域”，在這些“小區域”內，觀測點的密度較高，似乎呈現出“聚集性”；而且，它們或呈“二次多項式曲線形狀”或呈“三次多項式曲線形狀”分布。見圖1。

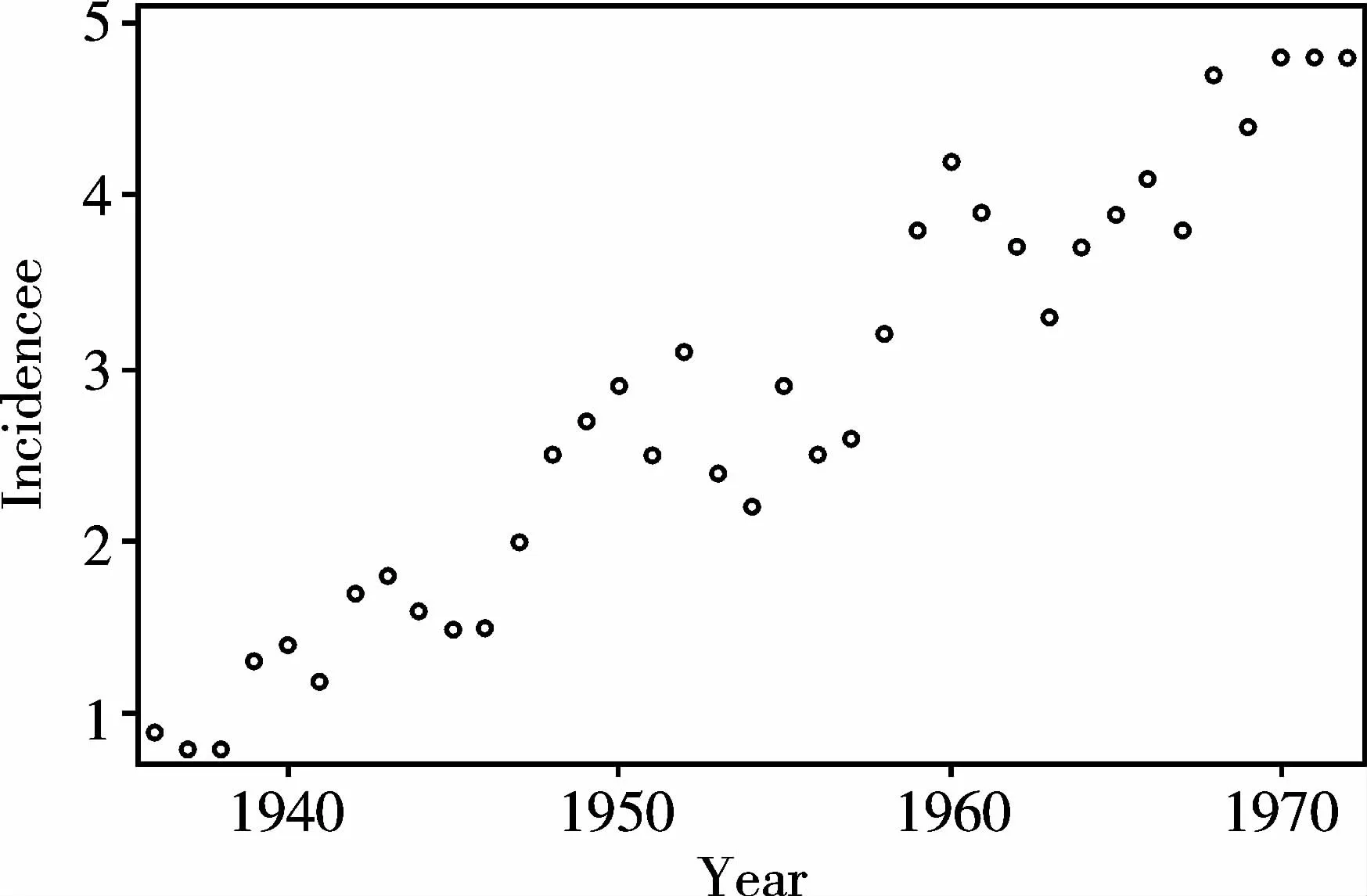
圖1 黑色素瘤發病率隨時間推移的變化趨勢

1.3 局部模型回歸分析的計算原理

1.3.1 計算原理

所謂局部模型，實際上就是在每個“小區域或小鄰域”上構建自變量的一個線性或二次曲線模型、甚至三次曲線模型。問題在于如何選取一系列的“小鄰域”。一個最直觀的想法是：將全部數據觀察點按自變量由小到大的順序排列，先確定由多少個相鄰的觀察點決定一個“小鄰域”，比如，設觀察點數目為k（k≥3），當k取一個確定數值后，就很容易將全部觀察點劃分成m個“小鄰域”。于是，在每個“小鄰域”上創建一個“局部模型”，計算出各“小鄰域”上因變量的殘差平方和，再求出所有“小鄰域”上殘差平方法和之和，就可獲得總殘差平方和。接下去，就可以改變k值，假定令k=3到k=n（即全部觀察點）共有j種情況，由前面的計算就可獲得某種情況下的“總殘差平方和”最小，于是，就認為按這種情況對應的“k值”來形成“小鄰域”是最合適的。

事實上，在SAS的LOESS過程中，評價擬合效果所選用的統計量為校正的赤池信息準則（AICC）（其取值越小越好，具體計算公式詳見后文），它所對應的k值被轉換成“光滑參數s”，s=k／n（其中k需要事先依據某種方法或理由初步估計出來，n為樣本含量或全部觀察點數目）。在每個“小鄰域”上建模時，采用“加權最小平方法”［2］。

1.3.2 常用的擬合效果評價指標

（1）赤池信息準則（The Akaike information criterion，AIC）：AIC是模型對資料擬合優度的一種度量，也體現了現在所使用的模型相對于最簡約模型之間的一種平衡。其定義如下：

AIC=-2LL+2p

上式中，p為模型中被估計參數的個數，LL是用于估計參數數值的似然函數的對數。

（2）AICC：

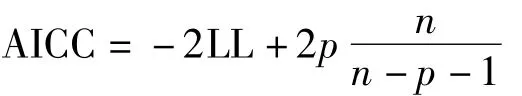
上式中，n為總樣本含量，其他變量含義同上。

（3）貝葉斯信息準則（Bayesian Information Criterion，BIC）與AIC和AICC是類似的度量，其定義如下：

BIC=-2LL+p log（n）

上式中，各變量的含義同上，此處不再贅述。

2 基于局部模型回歸分析解決實際問題［1］

2.1 問題與數據結構

【例1】下面是一個關于黑色素瘤發病率的資料。資料來自美國康涅狄格州腫瘤注冊部門，時間從1936年-1972年共37年，基于年齡校正的各年黑色素瘤的發病率（1／10萬）的前8年數據見表1，其他數據詳見后面的SAS程序：

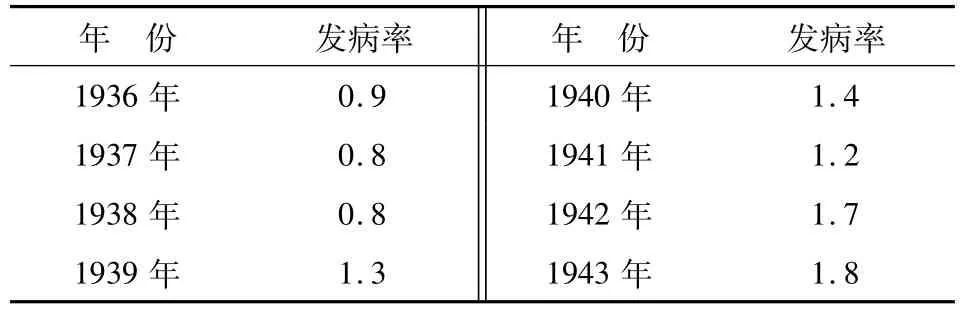
表1 基于年齡校正的1936年-1943年黑色素瘤發病率

【對數據結構的分析】嚴格地說，這是一個“時間序列”數據，即發病率隨著時間的推移而動態變化。為簡便起見，暫且將該數據視為一個計量因變量y（發病率）隨另一個計量自變量x（年份）變化的依賴關系問題。

【統計分析方法的選擇】研究y與x之間依賴關系的最簡單方法是進行直線回歸分析；若兩變量之間呈曲線變化趨勢，就可選擇某種曲線方程進行曲線回歸分析。

2.2 基于常規方法構建簡單線性回歸模型［3］

2.2.1 創建SAS數據集

創建一個名為“melanoma”的臨時SAS數據集的SAS數據步程序如下：data Melanoma；

input Year Incidences＠＠；

format Year d4.0；

datalines；

1936 0.9 1937 0.8 1938 0.8 1939 1.3

1940 1.4 1941 1.2 1942 1.7 1943 1.8

1944 1.6 1945 1.5 1946 1.5 1947 2.0

1948 2.5 1949 2.7 1950 2.9 1951 2.5

1952 3.1 1953 2.4 1954 2.2 1955 2.9

1956 2.5 1957 2.6 1958 3.2 1959 3.8

1960 4.2 1961 3.9 1962 3.7 1963 3.3

1964 3.7 1965 3.9 1966 4.1 1967 3.8

1968 4.7 1969 4.4 1970 4.8 1971 4.8

1972 4.8

；

run；

2.2.2 繪制散布圖，直觀展示兩變量之間的變化趨勢

利用下面的SAS過程步程序，可以繪制反映兩變量變化趨勢：

proc sgplot data=Melanoma；

scatter y=Incidences x=Year；

run；

【SAS輸出結果】

第1部分輸出結果為“圖1”，已經在前面呈現，此處從略。

由圖1可看出：散點呈上升的變化趨勢。但仔細觀察散點，發現在多個局部區域內散點表現為“聚集性”，并且呈“矩形”或“三角形”等形狀。

下面嘗試采用簡單直線回歸模型擬合該資料：

ods graphics on；

proc reg data=Melanoma；

model Incidences=Year；

run；

【SAS主要輸出結果】

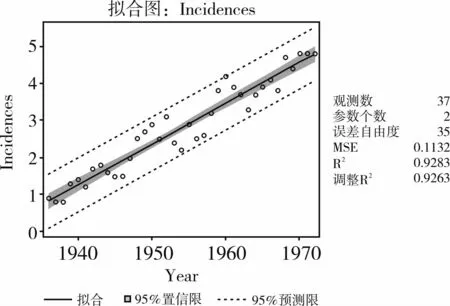
圖2 采用直線回歸模型描述黑色素瘤發病率隨時間推移的變化趨勢

擬合的統計量：均方根誤差=0.33641、R2=0.9283、調整R2=0.9263，從這些擬合統計量的數值來看，似乎用簡單直線回歸模型擬合此資料效果相當令人滿意。但從圖2可看出：在多個局部區域上，直線不能很好地給出預測結果。

2.3 基于局部模型構建非線性回歸模型［1］

基于局部模型構建非線性回歸模型的SAS程序如下：

proc loess data=Melanoma；

model Incidences=Year；

run；

【SAS程序說明】以上SAS程序調用LOESS過程擬合局部模型。

【SAS輸出結果及其解釋】

由圖3可看出：局部模型對此資料的擬合效果非常好，既沒有“過擬合”，也沒有“欠擬合”。

如何才能做到既不“過擬合”又不“欠擬合”？關鍵是要選取合適的“光滑參數”，它已顯示在圖3的左上角，即“Smooth=0.257”。用此數值乘以總樣本含量37等于9.5，說明程序按橫坐標軸的順序，將每相鄰9或10個觀測點所在的區域視為一個“局部區域”，在該區域上進行多項式擬合。

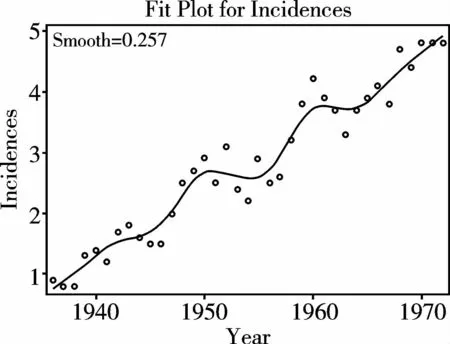
圖3 采用局部模型擬合的結果

如何獲得最佳“光滑參數”的數值？在SAS的LOESS過程中，先給定一系列的“光滑參數”值進行擬合，對于每個給定的“光滑參數”值，就能計算出若干個反映擬合效果或優度的統計量，其中，以AICC統計量取得最小值時對應的“光滑參數”為最佳。

利用如下SAS程序可以同時獲得4個“光滑參數”對應的擬合結果，

proc loess data=Melanoma plots=ResidualsBySmooth（smooth）；

model Incidences=Year／smooth=0.1 0.25 0.4 0.6；

run；

【SAS主要輸出結果】

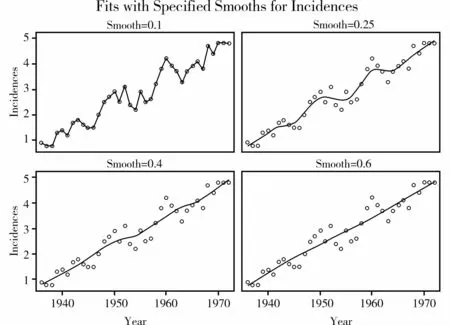
圖4 基于4個光滑參數進行局部模型擬合得到的擬合結果

在圖4中有4幅小圖，從上往下、從左往右的“光滑參數”依次為0.1、0.25、0.4和0.6對應的擬合結果。不難看出：“Smooth=0.1”屬于“過擬合”，而“Smooth=0.4”和“Smooth=0.6”屬于“欠擬合”，只有“Smooth=0.25”，屬于“正常擬合”，因為它已經是最佳“光滑參數”0.257的近似值。

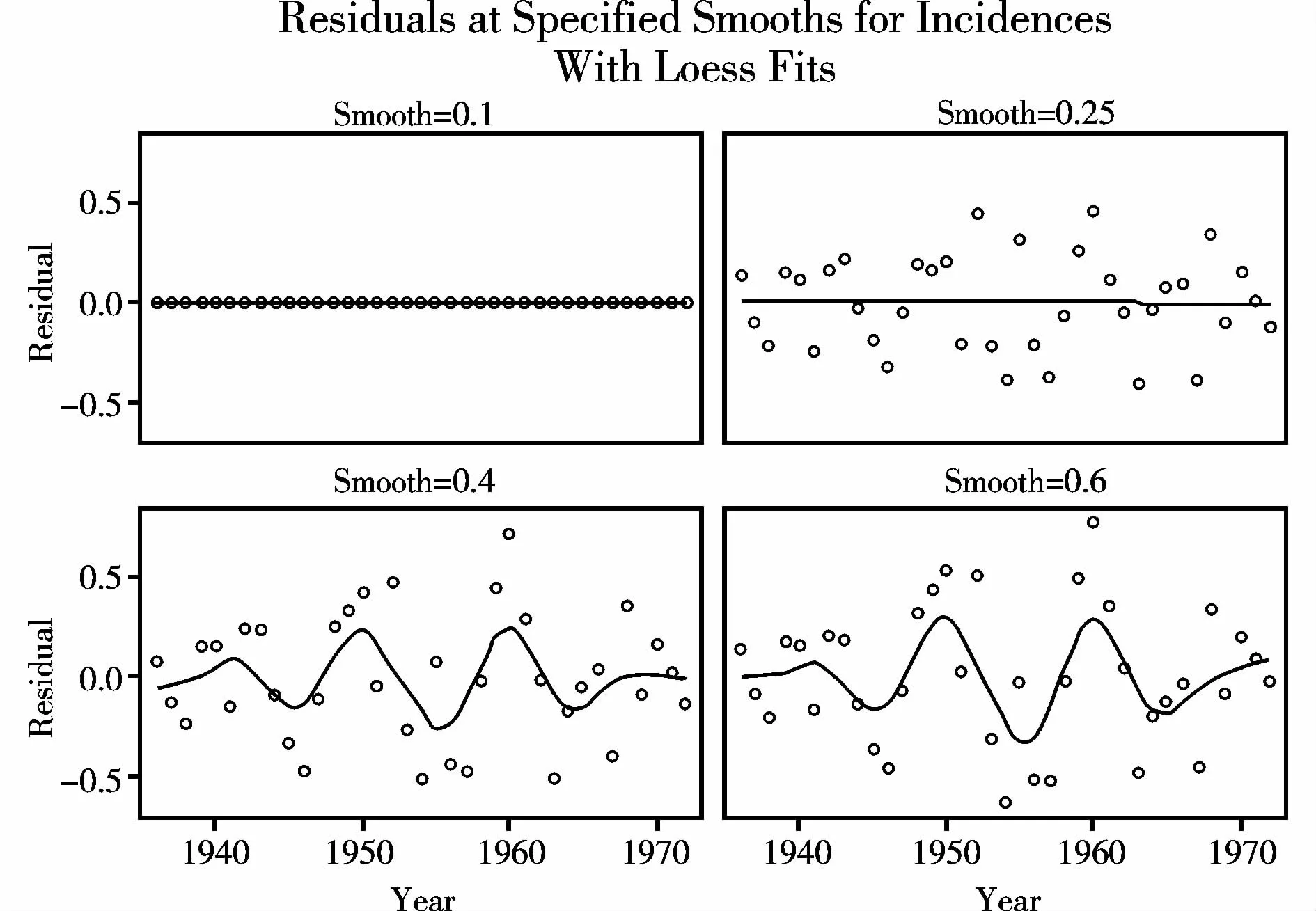
圖5 基于4個光滑參數進行局部模型擬合得到的殘差圖

圖5 中的4幅小圖分別與圖4中4幅小圖一一對應，只不過圖5反映的是殘差。當“Smooth=0.1”時，幾乎所有觀察點上的殘差都為0，這就是“過擬合”；當“Smooth=0.25”時，殘差圖上散點在各處波動接近且沒有明顯的變化趨勢，屬于“正常擬合”；而圖5中下面的2幅小圖都呈現出殘差散點具有一定的變化規律，屬于“欠擬合”。

為了避免盲目性，可以采用下面的SAS程序自動尋找到最佳的“光滑參數”的數值：

proc loess data=Melanoma；

model Incidences=Year／details（ModelSummary OutputStatistics）；

run；

【SAS主要輸出結果】

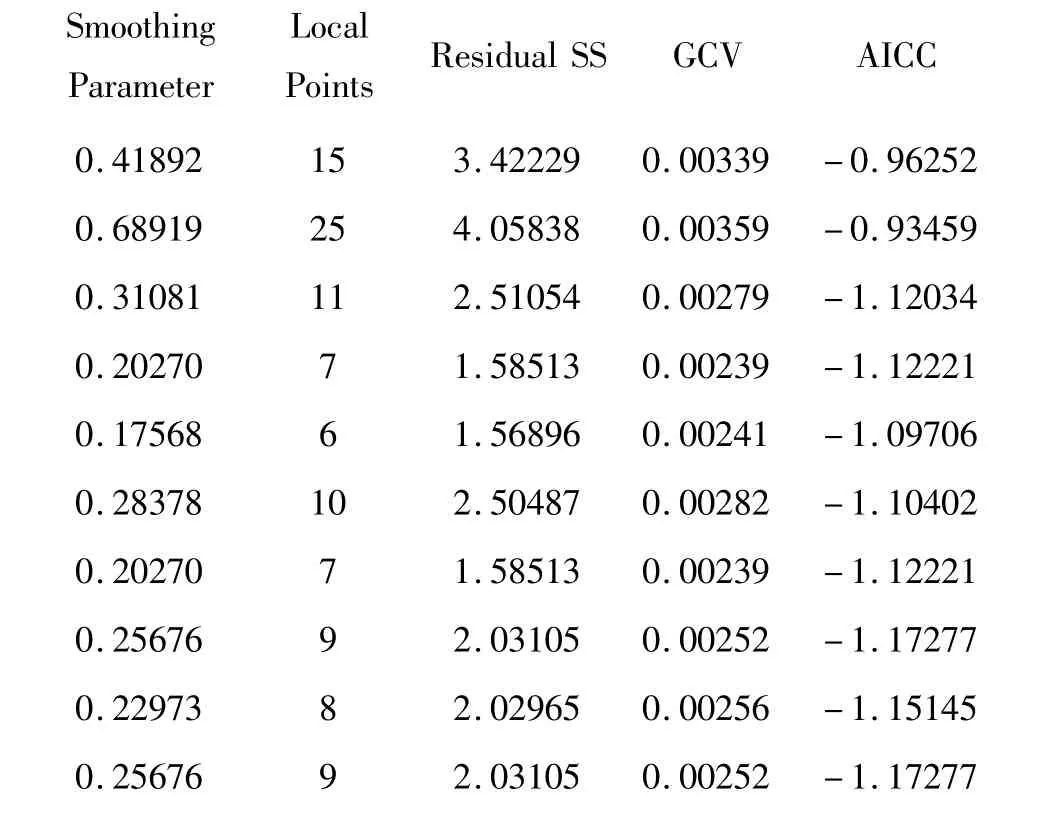
Model Summary

以上是程序自動尋找最佳“光滑參數”的動態過程，僅當局部觀測點為9個時，AICC統計量能取到最小值-1.17277，此時，對應的“光滑參數”為0.25676。

Fit Summary

以上是模型擬合效果的總結。

利用下面的SAS程序，可以得到擬合曲線的置信帶：

proc loess data=Melanoma；

model Incidences=Year／clm alpha=0.05；run；

【SAS主要輸出結果】

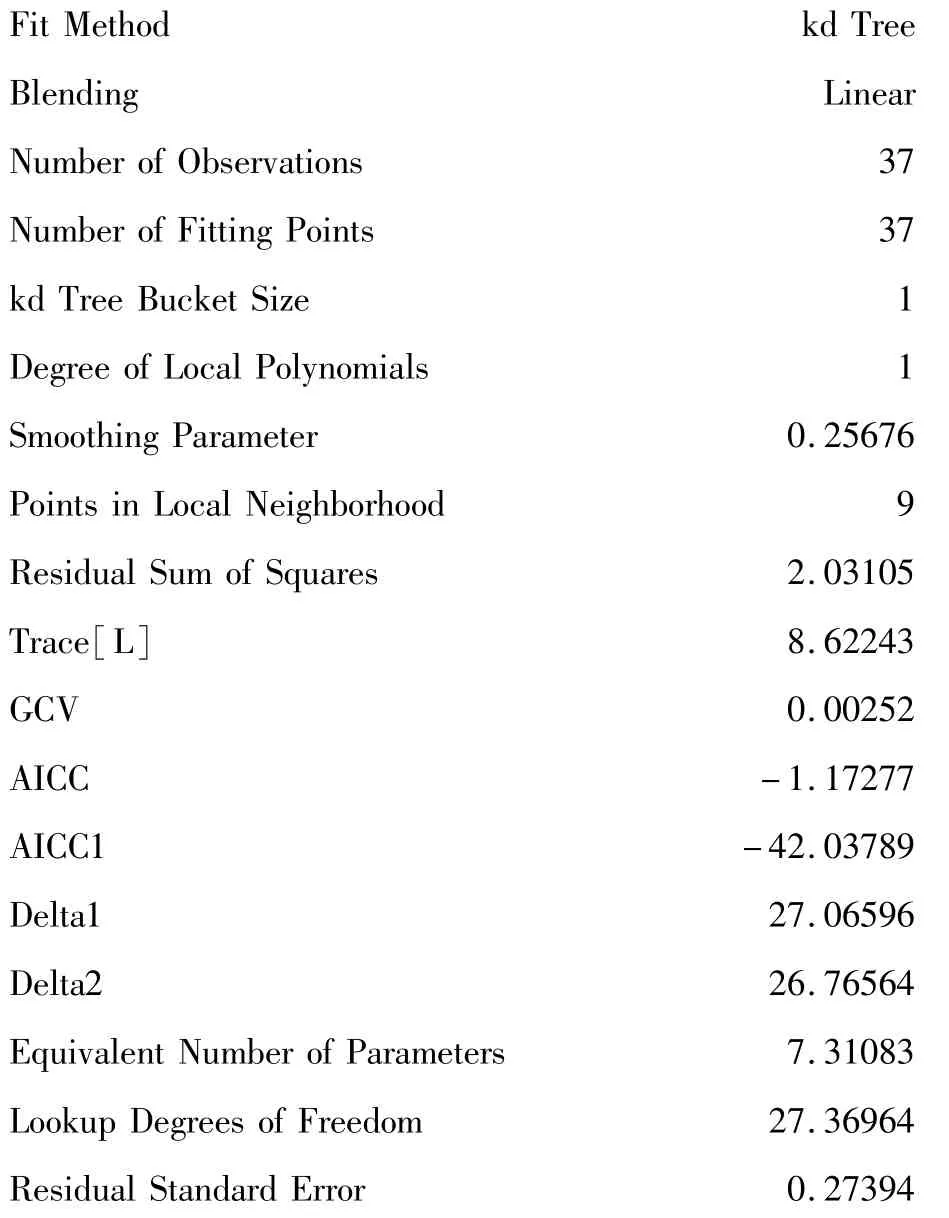
Fit Summary

以上是模型擬合效果的總結，與前面給出的結果基本相同。

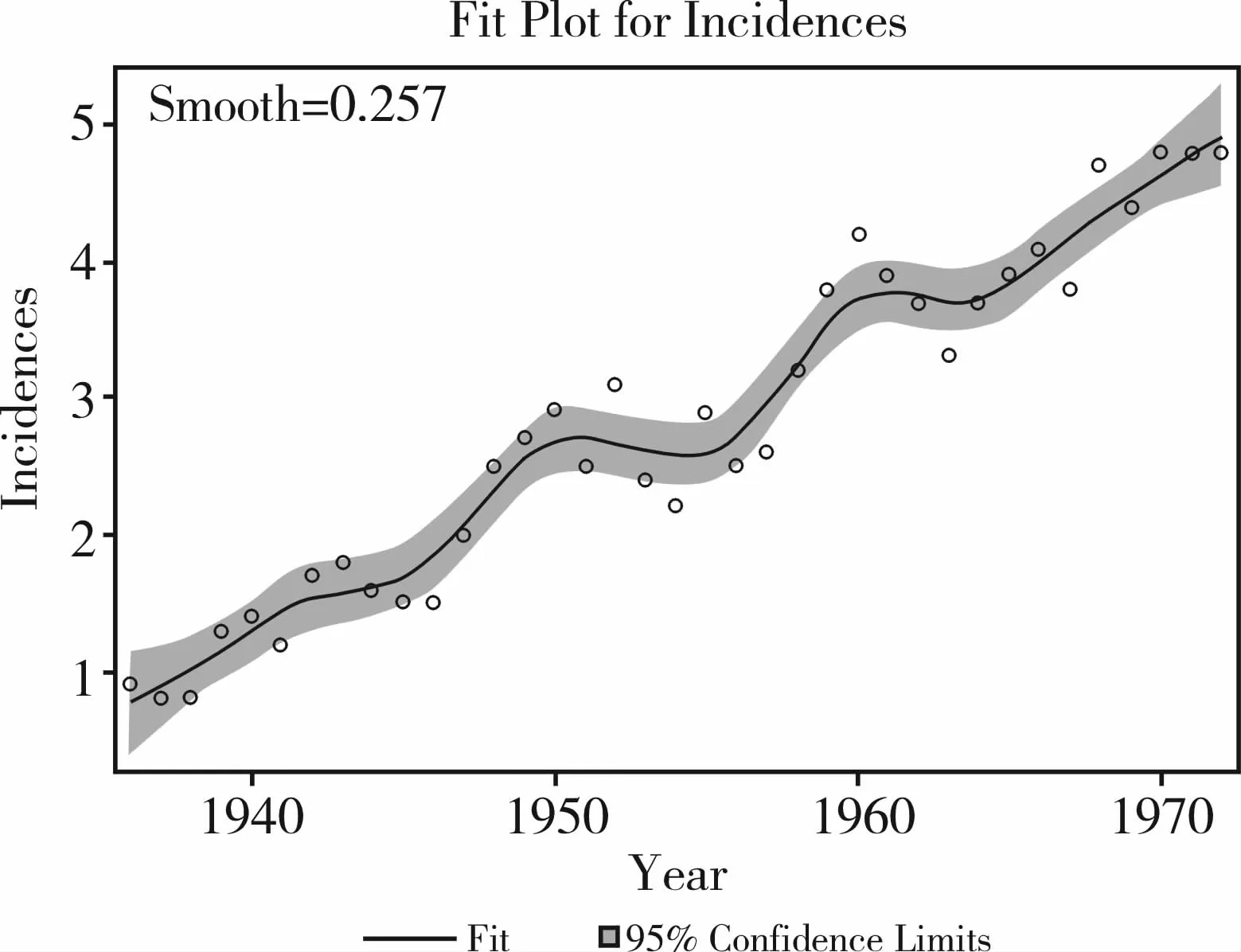
圖6 基于光滑參數為0.257時得到的局部多項式擬合結果及95%置信帶

2.4 小結

從上面的介紹可知：局部模型的關鍵在于選取“光滑參數”的具體取值。此值的真實含義是以每相鄰的多少個觀察點為一個“小區域”，在每個這樣的“小區域”上擬合一個“多項式”。當“Smooth=0.1”（相當于樣本含量的1／10的觀察點）時，得到了“過擬合”的結果。就本例而言，37／10=3.7≈4，若采用4次多項式，則多項式曲線就會通過每個觀察點；當“Smooth=0.6”（相當于樣本含量的 6／10的觀察點）時，得到了“欠擬合”的結果。就本例而言，6×（37／10）≈22，若采用 4次多項式，則多項式曲線就很難通過大多數觀察點。

當采用簡單直線回歸模型時，就相當于取“Smooth=1.0”，也就把全部觀察點所在的范圍視為一個“小區域”，采用一個“一次多項式”去擬合資料，這對于具有類似圖1中散點所表現的狀態是沒有任何幫助的。

由此可知：局部模型最適合用于如下的資料：全部觀察點呈現線性遞增或下降趨勢，而在多個“小區域”上表現為“二次曲線”或“三次曲線”或“四次曲線”的形狀。建模的目的只是為了形象化地擬合數據并對未知因變量的取值進行預測，而不需要呈現回歸模型的具體表達式（因此法不便給出具體的回歸模型）。