一種隨機共振增強正弦信號的二次多項式接收方法*

劉廣凱 全厚德 康艷梅 孫慧賢 崔佩璋 韓月明

1) (陸軍工程大學石家莊校區電子與光學工程系,石家莊 050003)

2) (西安交通大學數學與統計學院,西安 710049)

3) (中國人民解放軍66389部隊,石家莊 050000)

針對雷達、通信系統的正弦中頻信號在低信噪比中難以接收的問題,提出一種經隨機共振增強正弦信號的接收方法.通過分析正弦信號的隨機共振機理,引入判決時刻,將非自治的福克?普朗克方程(Fokker?Planck Equation,FPE)轉化為自治方程求解,得到FPE的含時間參量的周期定態解;在得到隨機共振輸出粒子的概率密度基礎上,通過分析能量接收、匹配濾波接收特點,提出基于二次多項式的接收結構,通過使偏移系數最大化,確定二次多項式系數,初步確定了檢驗統計量;為進一步減小誤碼率,結合“N次采樣取平均”思想,根據中心極限定理,將問題轉換為高斯分布下的假設檢驗問題,最終提出了隨機共振增強正弦信號的二次多項式接收方法和處理流程.仿真驗證了理論的正確性,并得到： 在最佳匹配隨機共振參數的限制下,當N=500時,二次多項式接收結構在信噪比大于－17 dB時誤碼率低于2.2 × 10－2.

1 引 言

傳統雷達、通信的中頻接收系統一般在信噪比(signal to noise ratio,SNR)大于0 dB時才能有效檢測和接收,如何使其中頻接收系統在強干擾或極低SNR的電磁環境中仍能正常工作,是軍事應急通信研究的重點內容之一.對偶序列跳頻(dual?sequence?frequency?hopping,DSFH)通信模式作為新型軍事應急通信手段,通過傳輸碼元0和1分別選擇兩組偽隨機序列控制的跳頻載波信道,選中的作為通信信道,而未選中的作為對偶信道,接收端通過檢測信道占用情況判斷傳輸碼元[1,2].與傳統通信模式將信息調制在基帶部分有很大不同的是,DSFH以兩條射頻序列出現與否代表碼元0和1,其信息調制在射頻部分.這種信息調制方式決定了只要某一支路的中頻正弦信號存在,接收碼元就判決為此支路約定代表的碼元[2].且一般采用較低數據速率,作為新的抗干擾通信模式,多用于高速率軍事通信受到強干擾無法實施時的應急通信.同時,一般采用超外差接收方式,其典型的中頻接收信號為正弦信號,是隨機共振(stochastic resonance,SR)系統的典型輸入信號形式之一.

SR作為一種非線性物理現象,當信號、噪聲與SR系統三者匹配時,噪聲通過非線性系統對信號檢測起到積極的增強作用,打破了以往認為噪聲總是有害的觀點.Benzi等[3]在對地球冰川期變化的研究中首次提出SR的概念,而后該現象在物理、生物、電子等領域得到印證[4?8],大量研究人員將其用于信號強度低于判決門限時的信號檢測接收問題[9].對于經SR處理后的信號檢測接收問題,關鍵在于設計合理高效的接收結構,即檢驗統計量.不同信號環境對應不同的最優接收結構,對此問題,大量學者展開研究.Galdi等[10]在高斯白噪聲環境下,應用最大似然檢測原理,分析了基于SR的最優接收問題,給出了平均值、過零檢測和非相干檢測三種檢驗統計量,初步解決了SR與信號檢測結合的問題.Zozor和Amblard[11]針對非高斯噪聲條件,討論了SR系統作為預處理單元如何檢測正弦信號問題,并在小信號假設下應用泰勒展開法,以SNR為指標得到了局部最優接收結構[12].Chen等[13,14]詳細討論了基于SR理論的信號檢測問題,推導了不同準則下的檢測概率和虛警概率,得到了廣義SR接收結構.Wang等[15]針對SR理論改進了傳統能量檢測結構,以SNR為指標,應用朗之萬方程(Langevin equation,LE)從粒子軌道角度進行了數值仿真.Zhang等[16]在α穩定噪聲情況下應用SNR指標,通過SNR取極值的必要條件,分析了單門限檢測接收SR增強后的信號及最優檢測門限問題.Zhang和Song[17]研究了色噪聲對邏輯SR信號的影響,得出在色噪聲環境下添加周期信號可以提高邏輯SR的檢測效果的結論.在得到合理高效的接收結構后,關鍵在于得到有無正弦信號這兩種假設下檢驗統計量的輸出概率密度,即求解表征SR系統輸出概率密度的福克?普朗克方程(Fokker?Planck equation,FPE)方程;但由于FPE中非自治項的加入,使得輸出無定態解[18,19],文獻[20]針對小信號特點從線性化角度分析了FPE的解問題,文獻[21]應用Meshless方法,得到了FPE的數值解,但目前所得的解形式很少應用于信號檢測問題.

針對正弦信號經SR系統增強后的檢測接收問題,通過分析正弦信號的SR機理,假設電磁粒子SR行為瞬時完成,引入判決時刻,將非自治的FPE轉化為自治方程求解,得到FPE的含時間參量的周期定態解;在得到SR輸出粒子的概率密度基礎上,通過分析能量接收、匹配濾波接收特點,提出基于二次多項式的接收方法,為進一步減小誤碼率,結合“N次采樣取平均”思想,根據中心極限定理,將問題轉換為典型的高斯分布下的假設檢驗問題,并給出了接收方法步驟和理論值;最后進行了仿真驗證.

2 隨機共振的信號增強機理分析

2.1 正弦信號的隨機共振描述

典型的隨機共振系統可由下面的朗之萬方程來描述：

其中a,b為非負參數;Acos(ω0t+φ) 為弱的外部周期驅動信號;Γ(t) 是高斯白噪聲,滿足E[Γ(t)]=0,E[Γ(t)Γ(t+s)]=2Dδ(s) ,參數D稱為強度.運用線性響應近似理論[3],可知系統(1)的長時間平均響應為

由于經典的隨機共振現象只能放大低頻信號,但在雷達、通信系統中,用作中頻信號的正弦波,其頻率一般在1 kHz左右,是典型大參數信號,因而無法直接應用SR理論,必須應用尺度變換將該中頻信號轉換為能被隨機共振機理處理的小參數信號.為此,引入以下歸一化變量代換[22]則(1)式轉化為

由此可見,我們的頻率尺度變換公式為ω0/a=2πf,即輸入信號經過歸一化尺度變換后變為低頻信號,其頻率僅為原來的 1/a;當a足夠大時,ω0/a就足夠地小.相應地,信號幅度變換公式為當a足夠大、b足夠小時,輸入信號經過歸一化尺度變換后變成了弱信號.與此同時,噪聲強度變為即給定的噪聲經由尺度變換也變成了弱噪聲.

注意到直接對朗之萬方程(3) 模擬一次,可以得到隨機過程x(t) 的一條樣本軌道,而在實際的應用當中,我們更關注的卻是大量樣本軌道的統計性質,因此常常需要對方程(3)做大量的隨機模擬.理論上,回避大量隨機模擬的方法是直接考慮隨機過程的概率密度函數.設ρ(x,t) 為粒子在時刻t位于位置x的概率密度,其演化滿足FPE[23]

和自然邊界條件.由于方程(4)是一個變系數的線性方程,其定態解不存在,但是可以證明其存在周期定態解[4,18];特別地,在絕熱消去意義上,可以得到方程(4)的周期定態解形如

其中Z(t) 是與t有關的概率歸一化常數.

2.2 SR增強后判決時刻的輸出概率密度

為了將概率密度函數(5)用于正弦信號的檢測接收問題,假設電磁粒子從瞬態進入周期定態的演化過程非常快,從而可忽略粒子從初始狀態向準平衡的周期定態演化的過渡時間;或者說,假定在引入判決時刻t0之時,電磁粒子的擴散運動已經達到了周期定態,且粒子在勢阱內的停留時間遠大于穩態過渡時間,即出現在勢阱內的概率遠大于其他位置的概率.假設勢阱由雙穩態的系統結構和正弦信號的極值點決定,從而以判決時刻t0時的周期定態概率密度表征SR輸出粒子在勢阱內的概率密度.

其中積分上下限x1,x2由概率歸一化常數決定,對于對稱雙穩態系統x1=-x2.

從(6)式可以得到,某判決時刻的正弦信號相當于在SR系統中添加了線性漂移力,會使粒子向兩側勢阱牽引,增加粒子在勢阱的出現和停留概率;正的漂移力牽引粒子向正側勢阱聚集,負的漂移力牽引粒子向負側勢阱聚集,但由于SR系統輸出粒子的對稱性和正弦信號的周期性,最終粒子的輸出概率密度呈現對稱性.同時,由于正弦信號的周期性,不同判決時刻正弦信號的大小不同,決定的漂移力大小也不同;當判決時刻位于正弦信號的波峰或波谷位置時,引入的線性漂移力最大,粒子在勢阱的停留時間最長,此時的概率密度最大.

3 二次多項式接收方法

3.1 檢驗統計量設計

目前通信系統多采用能量檢測、包絡檢測或匹配濾波方式接收,均可以看作廣義二次多項式形式的接收方式,基于此思想,提出經SR系統增強的正弦信號二次多項式接收結構如圖1所示.

如圖1所示,混有噪聲的正弦信號經過SR系統,得到增強后的待檢測信號x(t) ,經判決開關取樣,得到判決時刻t0的SR系統輸出值x(t0) ,即正弦信號波峰、波谷驅動SR系統的輸出值,此時x(t0)的概率密度可由(8)式計算得到.對x(t0) 進行二次多項式g(·) 運算,得到判決時刻的輸出值g(x0),且g(x0) 為正弦驅動信號處于波峰、波谷時,接收系統的輸出值;平均N個獨立同分布的g(x0) ,得到檢驗統計量Λ(t0) ;當Λ(t0)≥r0時判為H1(存在正弦信號),當Λ(t0)＜r0時判為H0(不存在正弦信號).

圖1 SR系統增強正弦信號的二次多項式接收結構Fig.1.Quadratic polynomial receiving structure for sine signals enhanced by SR.

當檢驗統計量服從高斯分布時,誤碼率Pe與偏移系數d存在解析關系,且高斯分布時,偏移系數非高斯分布時,Pe與d負相關[6,25].非高斯分布的偏移系數d定義如下[6,25]：

當g(·) 在二次多項式函數形式的約束時,通過使偏移系數d最大,確定g(·) 的系數.設二次多項式g(x)=l1x2+l2x+l3,則兩種假設下的偏移系數

由(8)式可得,二次多項式的偏移系數d(l1,l2,l3)與常數項l3無關,僅由系數l1,l2和x的一至四階原點矩決定,且d(l1,l2,l3) 有線性偏移不變性.令則

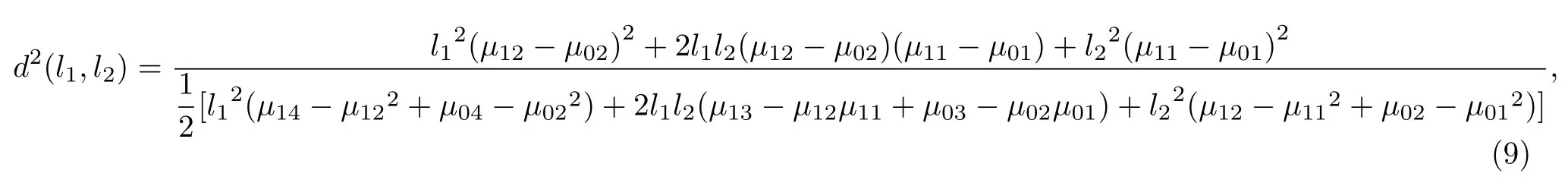
令

將(10)式代入(9)式得

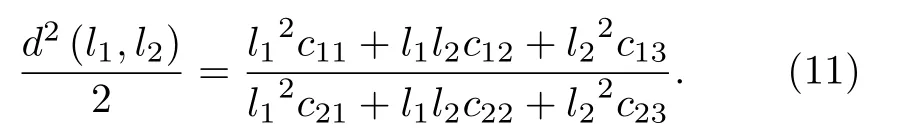
非高斯分布時,Pe與d負相關[6,25],所以欲得最小Pe,需計算最大d;通信系統多以最小誤碼率為準則,則問題轉化為

由函數取極值的必要條件得

設l1=ml2時即

求解(14)式可得m的數值解.此時g(x)=其在兩種假設下的期望和方差

其中μ1,σ1為g(x0) 在H1假設下的期望和標準差;μ0,σ0為g(x0) 在H0假設下的期望和標準差.

至此,經SR系統增強的二次多項式接收正弦信號問題轉化為經典的高斯分布下的假設檢驗問題.且正弦信號的接收中頻頻率先驗已知,當檢測到正弦信號存在時,接收碼元判定為“1”;否則判為“0”;以最小錯誤概率為準則,則誤碼率

其中r0為判決門限;μ1,μ0為兩種假設下g(x0) 單元的期望;σ1,σ0為兩種假設下g(x0) 單元的標準差.

對于最小錯誤概率準則,判決門限在兩種假設下概率密度相等,即f1(r0)=f0(r0) 時,Pe取得最小值,即

化簡得

則判決門限r0可由(19)式數值計算得到.

3.2 接收算法流程

根據3.1節的理論,經SR增強正弦信號的二次多項式接收算法如下：

1)根據(6)式計算兩種假設下SR系統輸出的概率密度函數ρ(x,t|H1) ,ρ(x,t|H0) 和一至四階原點矩μ11,u12,μ13,u14和μ01,u02,μ03,u04;

2)根據(10)和(14)式確定g(x) 的系數l1,l2;

3)根據(15)式計算g(x) 在兩種假設下的期望μ1,μ0和標準差σ1,σ0;

4)根據(19)式計算最小錯誤概率準則下的判決門限r0;

5)根據(17)式計算最小錯誤概率Pe.

4 仿真實驗

通過搭建基于SR增強的二次多項式接收正弦信號的Simulink模型,對比分析理論值和仿真值,驗證理論推導的正確性.仿真參數如下： 正弦信號頻率為1 kHz,中頻采樣率為200 kHz,最佳匹配SR的噪聲功率值參見文獻[22]的表3.

4.1 正弦信號經SR系統后的時、頻域波形

混合強噪聲的正弦信號時域、頻域波形分別見圖2(a)和圖2(b),經SR系統增強輸出后的時域、頻域波形分別見圖2(c)和圖2(d).當輸入SNR=－18 dB時,時域圖(圖2(a))和頻域圖(圖2(b))呈現出雜亂的、無規律的,無法看到1 kHz正弦信號分量的任何特征;然而經SR系統處理后,時域圖(圖2(c))出現周期性特征,說明存在周期分量信號;通過頻域圖(圖2(d))觀察到1 kHz出現明顯的信號分量(采樣點數20000個,頻率分辨率10 Hz,所以峰值出現在99.95處),且輸出全局SNR為－14.0957 dB,提高了3.9043 dB.這是因為SR單元對信號的處理可相當于非線性低通濾波,會增強低頻區的某些頻率分量,減弱其他的頻率分量.但與線性濾波器只改變輸出頻譜結構,不改變輸出各頻率的概率密度的性質不同的是,SR單元在改變頻譜結構的同時,也改變了輸出粒子的概率密度(見圖3).經過SR系統后,平坦分布的高斯白噪聲將向低頻區聚集,使低頻區能量變大,和低頻正弦信號一起驅動粒子在雙穩態勢壘之間躍遷,時域信號出現一定的周期特性,頻域觀察更顯著,改變了含噪信號的頻譜結構,宏觀上表現為SNR增大.

4.2 正弦信號經SR系統增強后的概率密度

正弦信號未經SR處理的粒子概率密度如圖3(a)所示,經SR系統增強后在不同位置的ρ(x,t)理論值和仿真值如圖3(b)所示,其部分局部如圖3(c)所示.黑色實線為有驅動力時的ρ(x,t0|H1),紅色虛線為無驅動力時的ρ(x,t0|H0) ,黑色實線為選取兩個不同的判決時刻,即分別為的對應時刻,無驅動力的情況可視為的對應時刻.在未經SR處理之前,正弦信號淹沒在高斯噪聲之中,且SNR極低,粒子的概率分布情況絕大部分表征了高斯噪聲的性質,因信號強度相較噪聲太小,導致有無信號時,兩種假設下的概率密度幾乎無差別,圖3(a)很好地說明了這一點.經過SR處理之后,粒子的分布不再服從高斯分布,體現了SR的非線性作用;同時理論和仿真曲線都表明,引入判決時刻的正弦信號相當于系統中添加了線性漂移力,會牽引粒子向兩側勢阱聚集,增長粒子在穩態勢阱的駐留時間,增加粒子在勢阱的出現概率,從而加大兩種不同假設下ρ(x,t) 的差異,更加有利于區分有無正弦信號這兩種假設,提高正弦信號的檢測能力.且根據兩條不同判決時刻的黑色實線可看出,不同判決時刻對應的正弦信號數值大小不同,決定的線性漂移力也不同,從而在兩側勢阱的概率也不同;當判決時刻位于正弦信號的波峰或波谷位置時,引入的線性漂移力最大,SR系統的粒子在勢阱的停留時間最長,在勢阱的概率密度也相應最大.從濾波角度來看,輸入粒子的高斯分布特性經過SR單元處理后,變為非高斯分布.但同時也可看到,有無信號驅動下SR輸出概率密度差異較小,導致直接將SR應用于DSFH的信號檢測出現較大的虛警;故而設計二次多項式接收結構和N次判決平均,進一步擴大接收檢驗統計量在有無信號下的概率密度差異,提高SR應用于DSFH的接收性能.

圖3 粒子處于不同位置時的概率密度(輸入SNR=－14 dB dB,噪聲功率 σ2=4 ,信號幅度 A=0.4 ,SR系統參數 a=1×104 ,b=2.6406×1012) (a)未經SR處理的粒子的分布概率;(b)經SR處理后粒子的分布概率;(c)經SR處理后粒子的分布概率局部圖Fig.3.Probability density function of particles of SR (input SNR=－14 dB,the noise intensity σ2=4 ,signal amplitude A=0.4 ,parameters of system a=1×104 ,b=2.6406×1012)： (a) The probability density of particles before SR processed;(b) the prob?ability density of particles after SR processed;(c) the partial of probability density of particles after SR processed.

4.3 不同判決點數的系統判決時刻輸出

不同判決點數N時系統在判決時刻的輸出仿真值如圖4所示,圖4(a)為單次檢驗統計量g(x0)的波形,圖4(b)為g(x0) 的多次(N=10)平均波形.可以看出不同N時,對于檢驗統計量g(x0) 的發散程度不同.這是因為判決時刻時,粒子的運動大部分集中于勢阱內,其位置由勢阱決定;但同時受到噪聲影響,粒子不會在勢阱內靜止不動,而是在一定范圍內抖動,出現圖4(a)中情形,其平衡位置就是勢阱的大概位置.圖4(b)為經過N次平均之后的波形,進一步體現了平衡位置所在,同時減小了隨機變量g(x0) 的抖動范圍.從而證明了N次平均統計量更有利于提高判決準確性.

圖4 不同N時 g(x0) 的輸出值(輸入SNR=－18 dB,噪聲功率 σ2=4 ,信號幅度 A=0.25 ,SR系統參數 a=1×104 ,b=3.3856×1012) (a) N=1時檢驗統計量的時域波形;(b) N=10時檢驗統計量的時域波形Fig.4.Output of g(x0) at different N (input SNR=－18 dB,the noise intensity σ2=4 ,signal amplitude A=0.25 ,parameters of system a=1×104 ,b=3.3856×1012)： (a) The waveform of test statistics when N =1;(b) the waveform of test statistics when N =10.

圖5 不同N時g(x0)的輸出概率密度(輸入SNR=－14 dB,噪聲功率 σ2=4 ,信號幅度A=0.4,SR系統參數a=1×104,b=2.6406×1012 ,g(x)=x2+0.0701x) (a) N=1時粒子的分布概率;(b) N=10時粒子的分布概率;(c) N=50時粒子的分布概率;(d) N=100時粒子的分布概率Fig.5.Output probability density function of g(x0) at different N (input SNR=－14 dB,the noise intensity σ2=4 ,signal amp?litude A=0.4 ,parameters of system a=1× 104,b=2.6406×1012 ,g(x)=x2+0.0701x)： (a) The output probability density when N =1;(b) the output probability density when N=10;(c) the output probability density when N=50;(d) the output prob?ability density when N=100.

不同判決點數N時系統的輸出概率密度理論值和仿真值如圖5所示,理論值為由E[g(x0)]和σ[g(x0)]確定的高斯分布,仿真值為系統的輸出頻率.從圖5(a)和圖5(b)可以看出,在N不符合中心極限定理條件時,系統輸出的頻率與高斯分布的概率密度相差較大;從圖5(c)和圖5(d)可以看出,當N＞ 50時,符合中心極限定理條件,系統輸出的頻率與相應的高斯分布符合較好;且隨著N的增大,系統輸出的方差σ2/N減小,粒子的聚集性更加集中,在均值附近出現的概率更大,更加有利于區分兩種不同的假設,理論和仿真均說明這一點.

4.4 不同接收結構的系統輸出誤碼率

不同接收結構的系統輸出誤碼率如圖6所示.可以看到,直接N次累積平均接收結構的誤碼率最大,其次是能量接收結構,二次多項式g(x) 接收結構的誤碼率最小;驗證了二次多項式接收結構的性能優于能量接收和直接累積平均接收結構,但三者性能相差不大.這是因為N次累積平均接收結構與包絡接收一致,而能量接收與包絡接收性能相差無幾.根據“3.2節 接收算法流程”中第二步： “根據(10)式和(14)式確定g(x) 的系數l1,l2”,同時依據偏移系數d的線性偏移不變性,可確定此時二次多項式g(x) 接收結構的最優系數為： 二次項系統為1,一次項系數分別為[0.4616,0.3312,0.2291,0.1421,0.1002,0.0701],常數項無影響,一次項系數較二次項系統相差較大,起主要作用的是二次項系數,所以和能量接收性能相差不大.同時,不同接收結構主要改變的是不同假設情況下系統輸出的期望,對于方差影響不大;而在高斯分布時系統輸出的誤碼率主要由方差決定;所以三者接收性能差別不大.

圖6 不同接收結構的系統輸出誤碼率Fig.6.Output bit error ratio of different receiving structure.

4.5 不同判決點數時系統輸出誤碼率

不同判決點數時系統輸出誤碼率如圖7所示.可以看到,隨著判決點數N的增大,系統輸出誤碼率越來越小,理論和仿真曲線均是如此.這是因為當接收結構一定時,系統輸出的期望是一定的,不同判決點數決定的是系統輸出的方差;在中心極限定理條件下,系統輸出在兩種假設時均服從高斯分布,其方差為σ2/N;隨著N的增大,方差減小,兩種假設的分離度越來越大,檢測接收的性能會越來越好.采用N點平均判決,必須確保一個碼元周期內存在N個可供判決的波峰、波谷值;即判決點數N越多,需要正弦信號在一個碼元時間內的周期越多,對于系統的采樣頻率和正弦信號載頻一定時,必須降低碼元速率,即通信系統中以“有效性換可靠性”思想的體現.在忽略兩種假設輸出概率密度差別二元對稱信道條件下,單符號的平均最大信息量c與誤碼率關系為c=1+Pelog2(Pe)+(1-Pe)log2(1-Pe),采用N點平均判決時,超外差接收的DSFH模式在某SNR條件下的最大信息速率R與誤碼率關系為Pelog2(Pe)+(1-Pe)log2(1-Pe)].當N=500時,二次多項式接收結構在SNR＞ －17 dB時誤碼率低于 2.2×10-2,可應用于DSFH通信模式的軍事應急通信.

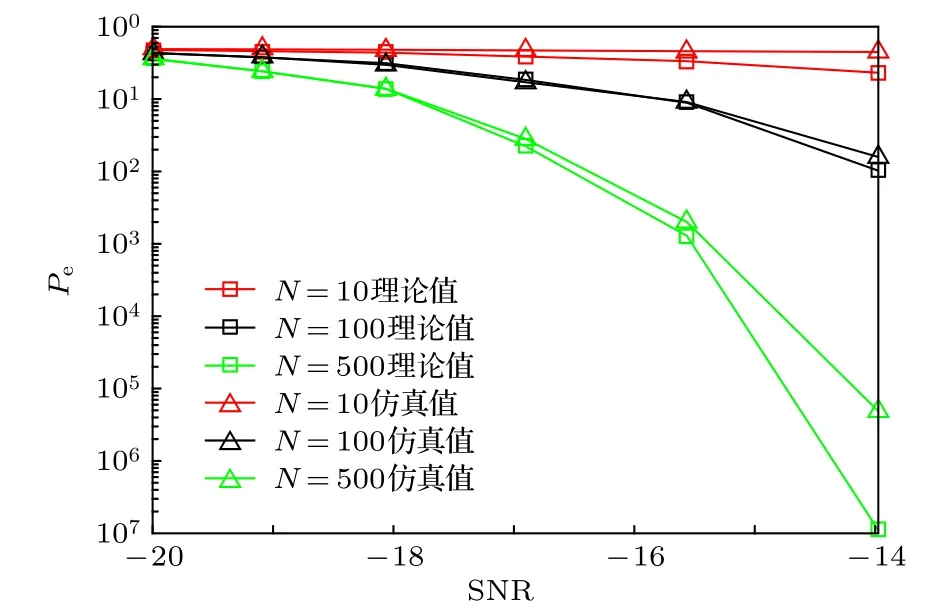
圖7 不同N時的二次多項式接收結構的誤碼率Fig.7.Output bit error ratio of quadratic polynomial re?ceiving structure at different N.

5 總 結

SR系統在輸入信號、噪聲和系統參數匹配的情況下,對低頻小信號有天然的共振效果,通過過采樣將超外差接收的DSFH中頻正弦信號等效到采樣頻帶的低頻區,此時噪聲會與低頻信號一起提高低頻區響應;加大了極低SNR下有無信號的區別,更有利于信號檢測接收.同時,SR應用于DSFH的信號檢測,并不會改變DSFH空域信號的窄帶特性,判決時刻對同步要求較低,非常適合于極低SNR下的軍事應急通信場景,進一步擴展了軍事應急通信的可用手段.信號檢測只關注在判決時刻的檢驗統計量情況,據此特點,一改傳統“先確定檢驗統計量,再確定判決時刻”的處理方法;同時根據雙穩態SR的勢阱特點,在確定檢驗統計量之前,引入判決時刻,巧妙地將非自治FPE轉換為自治FPE求解.根據SR和信號檢測的特點,合理改變判決時刻與檢驗統計量的處理順序的思想,以及所得ρ(x,t) 的求取方法及結果為SR應用于信號檢測接收問題提供了借鑒;所提的二次多項式接收方法進一步補充了正弦信號經SR系統增強后的接收策略.同時,多項式接收結構的冪次受系統穩定性的約束,這也是下一步的主要研究內容.