鉛基鈣鈦礦鐵電晶體高臨界轉變溫度的機器學習研究*

楊自欣 高章然 孫曉帆 蔡宏靈 張鳳鳴 吳小山

(南京大學物理學院,固體微結構國家實驗室,南京 210093)

鐵電材料由鐵電相轉化為順電相的臨界溫度被稱為居里溫度,是鐵電材料的一個關鍵指標.本文使用固溶體組成元素的基本物理性質等特征對不同組分和配比的鉛基鈣鈦礦鐵電固溶體進行了統一的描述,采用嶺回歸、支持向量回歸、極端隨機森林回歸等機器學習方法對鉛基鈣鈦礦鐵電固溶體的居里溫度進行了學習.使用交叉驗證的方法對學習效果進行驗證,得到上述機器學習方法對材料居里溫度的預測值與實驗值之間的平均誤差分別為14.4,14.7,16.1 K,集成三種回歸方法優化的模型在交叉驗證中測得的平均誤差為13.9 K.在此基礎上對超過20萬種鉛基鈣鈦礦的居里溫度進行了預測,給出了兩種可能具有高居里溫度的鐵電材料.

1 引 言

近年來,具有優秀壓電和熱電性質的弛豫鐵電體受到了廣泛關注.其中以固溶體Pb(Mg1/3Nb2/3)O3?PbTiO3(PMN?PT)為代表的鉛基鈣鈦礦鐵電體由于其高壓電系數而備受關注.然而PMN?PT的居里溫度較低(～130－170 ℃),限制了它在高溫場景下的應用.因此,為了解決這類鐵電體高溫應用的難題,研究者們在實驗中嘗試將Pb(In1/2Nb1/2)O3,Pb(Lu1/2Nb1/2)O3,Pb(Yb1/2Nb1/2)O3(PIN,PLN,PYN)等不同的簡單鈣鈦礦與PbTiO3結合在一起來形成二元或三元的鉛基鈣鈦礦固溶體來提高鉛基鈣鈦礦鐵電體的熱穩定性.

Liu等[1]研究者制備了一系列PLN?PT二元固溶體材料,其測得的居里溫度范圍為145－365 ℃.Wu等[2]研究者制備了一系列PIN?PMN?PT三元固溶體,測得的居里溫度范圍為188－231 ℃.

在實驗上類似的嘗試還有很多.然而將十幾種簡單鉛基鈣鈦礦與PbTiO3組合成二元或三元固溶體擁有超過100種可能的組合,再考慮到其中各組分比例的變化,可以看出該類體系的搜索空間是巨大的,通過實驗的方法窮盡所有可能的組合來尋找高溫鐵電體是非常困難的.在實驗方法之外,第一性原理計算的方法可以對材料的諸多電學性質進行模擬計算[3?5],然而目前該方法尚不能用來計算材料的居里溫度.

近年來,機器學習方法在物理、材料領域發揮了越來越重要的作用.在機器學習方法的指引下,人們可以快速地探索、挖掘出具有目標性質的材料[6?9].在本研究之前,就有研究者曾使用機器學習方法探索鈣鈦礦鐵電材料的居里溫度.例如Balachandran等[10]針對(1－x)Pb(B1,B2)O3?xPb TiO3體系從117種不同組分的數據中訓練得到機器學習模型,用以預測該體系的居里溫度,他們使用交叉驗證的方法進行模型評估,發現其最優模型的預測值與實驗值之間的平均絕對誤差(mean average error,MAE)為30.2 K;Zhai等[11]從47種鈣鈦礦材料數據中訓練得到了多個預測鈣鈦礦居里溫度機器學習模型,其表現最優的模型為支持向量回歸(support vector regression,SVR)模型,交叉驗證得到預測模型的MAE為21.2 K,預測值與實驗值之間相關系數為0.85.

為了進一步得到適用于鉛基鈣鈦礦鐵電晶體的、具有更高預測準確度和更具有魯棒性的居里溫度預測模型,本文通過利用元素屬性構建特征,從205種不同鉛基鈣鈦礦固溶體的數據中學習,得到三種預測居里溫度的機器學習模型.并且通過模型集成的方法對習得的模型進行集成,得到預測誤差更小的機器學習模型.據此對大量復雜鉛基鈣鈦礦的居里溫度進行了預測,以供實驗研究者參考.

2 方 法

本文構建機器學習模型來預測復雜鉛基鈣鈦礦的居里溫度主要包含以下3個步驟：

1)獲取訓練數據,構建用來預測居里溫度的特征;

2)通過交叉驗證的方法選取合適的機器學習模型并進行其超參數的調整;將多個模型進行集成,構建最終的機器學習模型;

3)使用機器學習模型學習訓練數據,對未知的復雜鉛基鈣鈦礦材料的居里溫度進行預測.

本工作使用了python庫scikit?learn[12]來進行模型的訓練和評估.

2.1 數據集及構建特征

我們從十余篇已發表的實驗論文中收集了205種不同的鉛基鈣鈦礦的居里溫度數據[1,2,13?28].其居里溫度的范圍為－120－490 ℃.其中涉及到18種簡單鉛基鈣鈦礦和45種前者組合而成的復雜鈣鈦礦.在這些鉛基鈣鈦礦中,鈣鈦礦結構的A位離子都為Pb離子,X位離子都為O離子,其居里溫度的差異是由B位離子的差異所導致的.在我們收集的訓練數據中既有結構較簡單的PbTiO3,PbZrO3等B位僅有一種離子的鈣鈦礦,也有PMN?PFN?PZT等B位有5種離子的復雜鈣鈦礦,這保證了學習得到的模型對于不同復雜程度的鈣鈦礦固溶體均有良好的泛化能力.

由于本研究的體系之間的差異僅在于鈣鈦礦的B位離子的不同,因此針對鉛基鈣鈦礦鐵電體的B位離子構建了以下特征來描述不同的材料：1)材料中不同種類B位離子所對應的化學計量占比、不同離子種類數目;2)對于材料中的B位元素,引入其離子半徑、電離能等39種的物理化學性質,該數據取自Balachandran等[10]的研究,針對材料中各元素的屬性及配比計算材料中B位元素化學計量占比加權平均得到的平均屬性和各種屬性的方差;3)采用第一性原理計算和機器學習方法得到的鈣鈦礦中B位離子偏移氧八面體中心的距離,取自文獻[29,30],計算其加權平均及方差.根據上述元素級別性質,對每種材料構建了86項特征用來描述不同材料之間的差異,并提供給機器學習模型用作建模的依據.所有特征的數值都進行了縮放,將特征數值縮放到均值為0、方差為1的范圍內,這樣可以確保所有的特征數值在相同的尺度上,從而避免由于特征尺度不同而對機器學習模型帶來誤導.得到特征向量x,作為后續不同機器學習模型的輸入.本文中采用的具體特征指標及取值在補充文件(online)中給出.

2.2 機器學習模型

如果僅研究某種特定組分的鈣鈦礦固溶體不同構成比例的材料的居里溫度,可以通過開展一系列實驗,制備出若干組分占比不同的材料,然后通過線性回歸等簡單方法進行擬合,并分析該組分的鈣鈦礦固溶體的居里溫度隨配比的變化.這種不依賴于額外物理知識和物理規律的統計方法難以推廣至各種不同組分的鈣鈦礦固溶體.僅能分析特定組分固溶體的居里溫度與配比的關系,而無法觸類旁通得對其他組分的材料居里溫度進行判斷.

為了克服這一缺點,發揮機器的“智能”來解決這一難題,構建了上述特征來對鉛基鈣鈦礦鐵電晶體進行描述,使用機器學習的方法從其基本的物理性質出發挖掘不同材料之間深層的相似性,將不同種類固溶體的知識納入統一的模型,達到“觸類旁通”的效果.基于這些基本物理性質和學到的不同固溶體居里溫度的知識,對完全未知的材料的居里溫度做出預言.

本文嘗試了多種機器學習模型來對該問題進行建模,其中效果較好的模型為： SVR[31]、極端隨機森林回歸(extremely randomized trees regres?sion,ETR)[32]、嶺回歸(kernel ridge regression,KRR) (使用徑向基函數(radial basis function,rbf)核)[33].

2.2.1 KRR (使用rbf核)[33,34]

KRR是線性回歸模型的拓展.線性回歸模型基于一系列的假設,例如： 目標值與特征之間呈現線性關系;特征之間應該相互獨立等.

為了將線性回歸推廣至更一般的場景,引入了KRR： 通過在線性回歸的損失函數中添加L2正則項來解決潛在的特征共線性的問題;引入了核技巧來使得模型可以擬合目標變量與特征之間的非線性關系.使用核技巧的KRR模型具有如下數學形式和損失函數[34]：

其中x為輸入的特征向量;λ為正則項的權重,是為了平衡結構風險與經驗風險而預先設定的超參數;Φ(x) 為將特征向量映射到高維希爾伯特空間的映射函數,其映射方法取決于核函數.本文采用的核函數K為機器學習中較為常用的rbf核,其對應了特征從原始空間到無窮維空間映射,核函數中的γ為預先設定的超參數[35].

模型在映射空間中使用線性模型進行數據建模,線性模型的權重w通過優化損失函數而得到.據此推導出使得損失函數最小的w：

式中定義Φ=Φai為數據集映射到高維空間后的特征矩陣,y=yi為目標向量.將該w代回(1)式中,并使用核函數代替高維向量的內積,得到

其中Kij=Φ(xi)TΦ(xj) ,κ(x)=K(xi,x).如果將核函數K(xi,x) 視為計算新樣本x與訓練樣本xi之間的相似度,那么可以認為使用核函數的KRR的預測結果是基于計算新樣本與訓練樣本之間的相似度的方法得到的.與訓練樣本相似的新樣本具有與之相似的元素級別特征,因而也會根據實驗已知的結論給出相似的預測結果.而與訓練數據較不同的樣本,則通過全局考察其相似性,來給出合理的預測值.

2.2.2 SVR[31]

SVR與KRR類似,具有線性模型的回歸形式.在SVR模型中,同樣采用核函數的方法為模型引入非線性擬合能力.而該方法與KRR不同的是,SVR對權重w進行優化時容許預測值與實驗值之間有ε的偏差,因此它不需要模型完美地滿足所有的數據點,可以減少模型過擬合的風險.具體地,它的損失函數如下[31]：

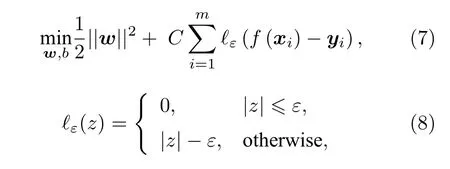
其中C為權衡結構風險與經驗風險的超參數;?ε為ε?不敏感函數,用以忽略數據與模型之間的較小偏差.在本研究中SVR的核函數選為徑向核函數.為了使得其損失函數最小化,通過構造拉格朗日函數并解其對偶問題,最終可以將SVR模型表示為

2.2.3 ETR模型[32]

為了嘗試使機器學習模型獲得更好的可解釋性,還使用了ETR模型對復雜鉛基鈣鈦礦的居里溫度進行建模.ETR將若干個分類與回歸樹(classification and regression trees,CART)集成在一起.其中每棵CART在構建時采用隨機挑選屬性和分裂值的分裂方法,從而構建出若干個完全隨機的樹.在ETR模型中,通過控制每棵樹的最大深度“depth”、劃分節點時最少的樣本數“min_samples”來限制樹的規模,通過控制總共集成樹的數量“n”來調節模型的擬合能力.

2.3 模型超參數的優化

2.3.1 交叉驗證策略

為了調整模型的超參數和檢驗模型的泛化效果,采用5次10折交叉驗證的策略.在一次10折交叉驗證中,將樣本集隨機劃分為10等份,輪流使用其中的1份作為測試集而其余9份作為訓練集.機器學習訓練集的數據而對測試集中的樣本的居里溫度進行預測,通過比較測試樣本居里溫度的實驗值與預測值之間的MAE、均方跟誤差(root?mean?square error,RMSE)來衡量模型對于未知樣本的預測能力.為了減少單次隨機劃分樣本集帶來的偶然性,以上過程重復5次,取結果的均值作為最終的評價依據.

由于本文研究對象分為簡單鉛基鈣鈦礦和復雜鉛基鈣鈦礦兩種,而簡單鉛基鈣鈦礦的種類有限且研究較為詳盡,同時本研究的主要目標－復雜鉛基鈣鈦礦種類繁多,相對而言已研究確認的材料較少,因此在交叉驗證的過程中將數據集中B位元素種類小于3的24項簡單鈣鈦礦的數據作為“教師”,只出現在訓練集中用來模型訓練,不出現在測試集中參加模型性能的評估.

2.3.2 超參數的優化

模型的超參數直接影響了模型的擬合能力和擬合策略,選取一組合適的超參數對模型的構建非常重要.在定義了交叉驗證的策略之后,在一定的超參數區間內通過隨機搜索[36]和網格搜索的方式選取若干組超參數并使用該超參數構建模型.通過之前定義的交叉驗證策略對模型效果進行檢驗,最終選取使得交叉驗證結果最理想的一組超參數作為模型最終的超參數.

例如,當優化SVR中的超參數ε時,在0－10的取值范圍內以0.5為步長對ε進行網格搜索.如圖1所示,對比了ε取不同值時模型的測試誤差,同時將該參數模型應用于全部數據集時的支持向量數目也一并列出,以作參考.當ε取值小于4時模型的誤差較低;當ε取值進一步增大時模型的誤差出現快速上升.另一方面隨著ε取值的增大,模型中的支持向量的數目也在減少.在泛化能力相似的情況下,傾向于選擇較簡單的模型以避免過擬合,因此ε的值最終取為4.此時,模型經過完整地學習訓練集中所有205項數據后,其模型中的支持向量數目為147項,也就是說模型僅使用其中147項材料的數據對未知材料進行預測.

圖1 支持向量回歸中的超參數ε的優化及支持向量數目分析Fig.1.Optimization of hyperparameters in support vector regression and the analysis of the number of support vec?tors.

依據上述方法,同樣對其他超參數做了類似的搜索和優化,最終得到的超參數如表1所列.

表1 本文三種機器學習方法所采用的超參數Table 1.Hyperparameters of the three machine learning methods in this study.

2.4 模型的集成

上述三種模型,從不同的角度出發對鈣鈦礦鐵電材料的居里溫度進行了學習,均取得了良好的成效.為了進一步提高預測的準確度,通過集成的方法,將上述三種回歸模型融合為一個統一的模型.集成模型同時訓練上述三種機器學習模型,并使用三種模型分別對居里溫度進行預測.將三種機器學習模型的預測均值作為最終的輸出.

為了檢驗集成的效果,也對集成模型使用交叉驗證的方法進行了評估.另外,也嘗試了賦予三個模型其他合理的權重,如圖2所示,當將三種模型融合在一起時,往往可以得到比最優單模型更好的效果.測得的最優融合比例為0.6∶0.2∶0.2 (KRR∶SVR∶ETR),其MAE為13.7 K.等權重模型融合測得的MAE為13.9 K (圖2中的紅色點).出于保持模型簡單性的考慮,直接采用了等權重的方法對模型進行融合.

圖2 不同模型權重的融合實驗結果Fig.2.Performance of ensembled model with different base model weight.

2.5 使用機器學習方法對未知材料探索

對數據集中出現的20種不同組分的簡單鉛基鈣鈦礦相互組合,得到了大量的包含PbTiO3組分的二元或三元的復雜鈣鈦礦固溶體,共有190種可能的組合方式,而在這些復雜鈣鈦礦固溶體中,使其中簡單鈣鈦礦組分從2%開始,以2%為步長變化,從而研究不同組分的復雜鉛基鈣鈦礦.至此,得到了超過20萬種鉛基鈣鈦礦材料.使用上文中的方法對它們構建特征,并使用機器學習的方法對其中所有材料的居里溫度進行預測.

3 結果與討論

3.1 模型效果驗證

在5輪的交叉驗證中,使用了MAE,RMSE和相關系數三項指標對三種機器學習模型和集成后模型的預測結果進行了評估.評估結果列于表2,在三種學習模型中KRR給出了最低的MAE,為14.4 K,同時RMSE為最低的22.5 K.所有模型的在交叉驗證中對于未學習過的材料的預測值與材料的實驗值之間均有較大的相關系數.而將三種機器學習模型進行集成后,集成模型的表現比三種機器學習模型更為優秀.同時在表2中也將本文機器學習模型與其他使用機器學習方法研究鈣鈦礦居里溫度的工作中的最優模型進行了比較.

表2 本文所使用的機器學習方法的評估及與其他研究者工作的對比Table 2.Evaluation of machine learning methods in this paper and the comparison with other works.

為了給讀者更直觀地展示各種機器學習模型對于未知材料居里溫度的預測效果,給出了5輪交叉驗證過程中不同材料的預測均值與實驗值,如圖3所示.圖3中不同的橘色點對應不同的材料,其縱坐標為該材料的居里溫度實驗值,橫坐標為本文機器學習模型對該材料居里溫度的預測均值.藍色點劃線y=x代表著預測值與實驗值完全吻合的理想情況.從圖3可以看出在交叉驗證過程中對于大部分未學習的鉛基鈣鈦礦,機器學習模型對其居里溫度的預測值都落在其實驗值的附近,預測值與實驗值之間具有較強的相關性.

圖3 三種機器學習模型及其集成模型對材料的預測值與實驗值的比較Fig.3.Comparison of prediction and experimental values of three machine learning models and their ensemble models.

此外,在圖3中對比三種機器學習模型不難看出,這三種機器學習模型一致得給出了不錯的預測成績,但是其對于特定材料的預測結果卻不盡相同,這是由模型之間的差異所導致的.如上文所述,KRR模型與SVR模型具有相同的廣義線性回歸形式,相同的核函數形式.但是其不同的損失函數賦予了兩種模型不同的“價值觀”,在學習過程中它們遵從各自的“價值觀”各自尋找其最優參數,最后得到的結果必然是不同的.ETR模型基于CART,與前兩種模型形式顯著不同,在交叉驗證中,其MAE與RMSE也略遜于前兩種模型,但是其樹的形式更利于人類理解.同時如圖2所示,融合更多的模型也有助于提高模型的預測能力,因此將這三種模型融合在一起,相互取長補短,得到了預測能力更優的集成模型.例如支持向量模型對于實驗值50 K附近的某材料的預測值發生了明顯的偏差,經過模型融合之后,該偏差得到了有效的緩解.

3.2 模型成果

本文的產出主要分為兩方面： 本研究中整理的鉛基鈣鈦礦的居里溫度數據和本文中構建的機器學習模型;對超過20萬種鉛基鈣鈦礦材料的居里溫度進行了預測,并挑選了兩種可能具有高居里溫度的材料以供實驗研究人員參考.

3.2.1 數據與模型

在本研究中收集的包含205種鉛基鈣鈦礦的居里溫度數據集在補充文件(online)中給出,可以供其他相關領域的理論或實驗研究者參考和使用.利用該數據集,本文構建了三種機器學習模型：KRR,SVR,ETR.與多數研究者不同的是,還將這三種機器學習模型集成為一個模型.

為了檢驗單個機器學習模型和集成機器學習模型的可靠性,本文通過交叉驗證的方法對模型進行測試.在交叉驗證的過程中KRR,SVR,ETR單模型的MAE分別為14.4 K,14.7 K,16.1 K.集成后的機器學習模型在交叉驗證中的MAE為13.9 K.而在其他研究者對鈣鈦礦鐵電體的居里溫度進行預測的而建立的模型,其交叉驗證的MAE為30.2 K[10]和21.2 K[11].該交叉驗證誤差的差異可能來源于模型構建過程中特征構建的方式不同等因素,因此本文中使用元素屬性的均值和方差構建特征的方法擁有一定的泛化意義.

此外,使用ETR模型學習后,可以根據CART在不同特征上進行分裂時的方差變化來量化不同特征對于材料居里溫度的重要性.具體而言,ETR模型是多棵CART的總和,CART在其每個節點中以某個特征的取值作為分割點將節點中的樣本分割至兩個子節點(一個節點中的樣本對應特征取值均大于等于該值,另一個節點中的樣本對應特征取值均小于該值).本文采用節點中樣本居里溫度的方差來刻畫節點中樣本的離散性,采用分裂前后的加權方差變化來刻畫該分裂帶來的聚合增益.如果依據某特征值將樣本分為兩類時帶來了較大的聚合增益,也就是說依據樣本該特征的值可以將節點中具有較高居里溫度的樣本和居里溫度較低的樣本更好地區分開來,那么該特征的取值對于判斷居里溫度顯然是重要的.將所有節點上采用某特征的取值作為分割條件時的方差變化以其節點中的樣本數量作為權重加權求和,得到該特征對于預測材料居里溫度的重要性.該指標表示了在使用ETR模型預測居里溫度時該特征的重要程度[37].

將所有特征重要性進行了歸一化,并將重要性最大的五種特征表示在圖4中.圖4所示為B位元素(或該元素最常見單質)的熱導率均值、電導率均值、比熱容方差、元素序數均值、鈣鈦礦中離子偏移均值,五種特征在使用ETR模型預測材料的居里溫度中起到了最重要的作用.

圖4 ETR模型中最重要的5項特征Fig.4.Five most important features in ETR.

3.2.2 使用機器學習尋找高溫鉛基鐵電體

使用集成的機器學習模型,對數據集以外的超過20萬種鉛基鈣鈦礦材料的居里溫度進行了預測,并挑選出了0.02PbMn1/2Nb1/2O3?0.98PbTi O3(0.02PMN?0.98PT),0.02PbGa1/2Nb1/2?0.02Pb Mn1/2Nb1/2O3?0.96PbTiO3(0.02PGN?0.02PMN?0.96PT)兩種具有較高居里溫度的鉛基鈣鈦礦固溶體,其對應的居里溫度分別為481 ℃和466 ℃.集成機器學習模型對于PGN?PMN?PT體系中不同組分權重所形成的一系列固溶體進行的預測結果如圖5所示.

圖5 集成機器學習模型對PGN?PMN?PT固溶體的居里溫度的預測Fig.5.Prediction of Curie temperature of PGN?PMN?PT solid solution by ensemble machine learning model.

此外,在補充材料(online)中還提供了全部20余萬種鈣鈦礦固溶體的居里溫度預測數據來為實驗研究提供更詳盡的參考.

4 結 論

本文在不同組分和配比的鉛基鈣鈦礦鐵電晶體所形成的龐大搜索空間中尋找具有高居里溫度的鐵電體,利用元素基本物理性質等信息構建了一系列特征,得以對各種不同組分的鉛基鈣鈦礦鐵電晶體進行統一的描述,從而使得機器可以從基本物理性質出發對固溶體的居里溫度進行建模和預測.分別使用了KRR,SVR,ETR三種機器學習方法對鉛基鈣鈦礦鐵電固溶體的居里溫度進行了學習,并使用了等比例融合的方法構建了集成學習模型.

采用交叉驗證的方法對模型的可靠性進行了評估,其中集成機器學習模型在交叉驗證中測得MAE為13.9 K.使用該方法對超過20萬種鉛基鈣鈦礦鐵電體的居里溫度進行了預測,并挑選出了兩種具有潛在高居里溫度的鉛基鈣鈦礦鐵電晶體：0.02PMN?0.98PT,0.02PGN?0.02PMN?0.96PT.