基于蒙特卡羅-離散縱標方法的氘氚激光等離子體聚變反應率數(shù)值模擬*

陳忠 趙子甲 呂中良 李俊漢 潘冬梅

1) (西南科技大學國防科技學院,綿陽 621010)

2) (國防科技大學文理學院,長沙 410073)

3) (中國科學技術大學,合肥 230027)

慣性約束聚變(ICF)是實現(xiàn)受控熱核聚變可能途徑之一.聚變中子源項是氘氚激光等離子體物理設計與分析的重要參數(shù)之一,其準確性直接影響分析結果的可靠性.目前國內外對于ICF氘氚聚變反應產(chǎn)生的中子源項研究主要基于解析公式法,在溫度和反應類型等方面適用范圍有限.本文采用粒子云概念對氘、氚粒子云團開展了隨機抽樣與時空網(wǎng)格劃分,然后基于麥克斯韋速率分布律對氘氚聚變反應開展了多普勒能量展寬效應分析與微分截面溫度修正工作,耦合蒙特卡羅方法和離散縱標方法,開展了激光等離子體中D?T粒子云團聚變反應率的數(shù)值模擬工作.研究結果顯示,與原核數(shù)據(jù)庫截面相比,D?T,D?D,T?D截面經(jīng)修正后多普勒溫度效應顯著.在20－100 keV的等離子體溫度范圍內,相較傳統(tǒng)的解析公式法,本文模擬結果更符合最新的ENDF核數(shù)據(jù)庫的氘氚反應截面數(shù)據(jù),且與解析公式法結果在低能區(qū)存在較大誤差,可能是計算方法不同與低溫截面差異過大原因導致.

1 引 言

慣性約束聚變(ICF)是實現(xiàn)受控熱核聚變可能途徑之一[1,2].點火是研究慣性約束核聚變的關鍵,所獲得的聚變中子源項是激光等離子體物理設計與分析的重要參數(shù)之一,其準確性直接影響分析結果的可靠性[3?14].目前國內外對于ICF氘氚聚變反應產(chǎn)生的中子源項研究主要基于解析公式法,如對于氘氚各占50%密度的情況,其產(chǎn)生率計算公式為

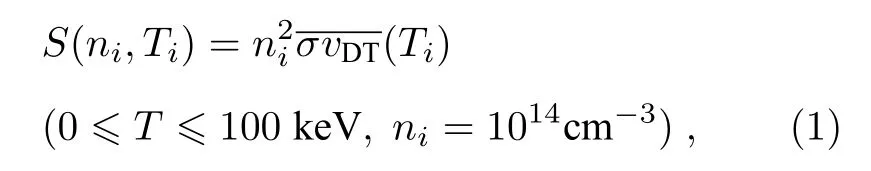
其中,S(ni,Ti)為中子產(chǎn)生率,ni為氘或者氚粒子密度,Ti為等離子體溫度,σ為反應截面,vDT為麥克斯韋分布下的氘氚粒子相對速度,表示兩者的加權平均[15].

目前大量使用的解析公式法主要針對氘氚粒子密度相同且溫度不大于100 keV,在溫度和反應類型等方面適用范圍有限.本文通過結合蒙特卡羅(MC)方法和離散縱標(SN)方法,開展了激光等離子體中D?T粒子云團聚變反應率的數(shù)值模擬算法程序設計.

2 算法設計

2.1 物理模型與碰撞物理過程

對于所給定的氘氚等離子體集團,在進行模擬時,由于數(shù)據(jù)量過于龐大,不可能把每個粒子都進行聚變反應的模擬,因此本文首先引入了粒子云概念,即多個位置、速度相同的同類粒子的集合,且認為粒子云所發(fā)生的作用均為同一反應.其次使用了網(wǎng)格模型,即將所模擬的時空進行了網(wǎng)格劃分,其中整個等離子體空間經(jīng)網(wǎng)格化后構成一個三維的空間坐標,一個空間網(wǎng)格中可包含多個粒子云.

氘氚等離子體為大量粒子組成,滿足麥克斯韋速率分布律,即

其中,m為粒子質量,k為玻爾茲曼常數(shù),T為等離子團溫度.

本文選取了ENDF/B?VI和ENDF/B?VII的氘氚聚變反應數(shù)據(jù)庫,其所給出的粒子能量為系統(tǒng)的質心系能量,因此需要將實驗室系下入射粒子與靶粒子碰撞時的對應能量轉換為質心系能量.等離子體中,氘、氚粒子由于速度和質量不同,用動量來進行矢量合成.根據(jù)動量守恒

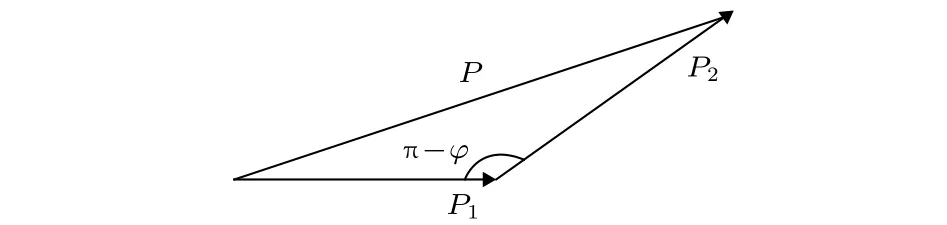
圖1 動量矢量分解Fig.1.Momentum vector decomposition.

將(3)式寫成標量形式：

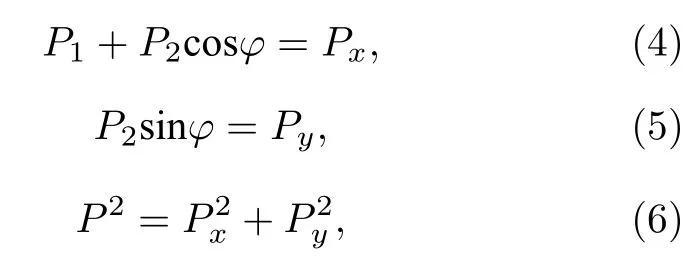
其中,?為兩矢量夾角,Px和Py分別為質心系動量的x軸和y軸分量.?角即為需要離散化處理的角度分布.

所模擬的物理過程為： 某一隨機位置處,具有某一隨機速率的入射粒子云沿某一隨機方向發(fā)射,則根據(jù)核反應率的計算原理,沿途路徑上的所有網(wǎng)格,均認為入射粒子云與其中所有粒子發(fā)生反應,且按照截面大小發(fā)生核反應.由此,在一個時間網(wǎng)格內,氘氚聚變反應的中子產(chǎn)生率為

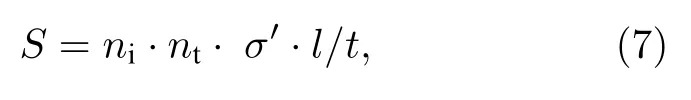
其中,S為中子產(chǎn)生率;ni為入射粒子的數(shù)密度,nt為靶粒子的數(shù)密度,當氘氚粒子各占50%時,ni=nt;σ′為修正后的氘氚聚變反應截面;t為模擬的時間步長;l為入射粒子云在一個時間網(wǎng)格內走過的路程.

2.2 時空網(wǎng)格劃分與誤差控制

氘氚等離子體發(fā)生聚變,并實現(xiàn)可持續(xù)慣性熱核聚變燃燒,必須滿足以下3個基本條件：

1)勞森判據(jù)條件niτ≥1014s/cm3;

2)燃料等離子體溫度條件Th≥5×107K ;

3)ρr乘積條件ρmr≥3g/cm2;

其中,ni為熱核燃料等離子體密度,τ為由慣性維持該離子數(shù)密度不變的時間間隔,ρm為被壓縮的低溫熱核燃料質密度,r為預壓縮到高質密度熱核燃料小球的半徑[16].

為減少氘氚聚變反應率計算誤差及計算量,激光等離子體的時空網(wǎng)格劃分極為重要.從誤差產(chǎn)生源來看,假設入射粒子云所經(jīng)過的網(wǎng)格,均要計算其內部的粒子云與入射粒子云的反應,但如果入射粒子云只經(jīng)過網(wǎng)格邊緣部分,則其內部大部分粒子云并沒有與入射粒子云發(fā)生碰撞,由此導致誤差.以二維網(wǎng)格為例,如圖2所示.

圖2 二維網(wǎng)格誤差分析Fig.2.Two?dimensional grid error analysis.

圖2中的灰色網(wǎng)格代表著僅其邊緣部分被入射粒子云穿過,可以看出,若將該類網(wǎng)格均計入氘氚聚變反應,模擬結果將由此偏大.同樣,入射粒子云的初始點和終點位置也會造成誤差,如圖3所示.

圖3 二維網(wǎng)格大小造成的誤差Fig.3.Error caused by two?dimensional mesh size.

圖3給出了兩個入射粒子云,由于終點位置的不同,導致實際路徑長度差別接近一個網(wǎng)格.因此,網(wǎng)格劃分越細,則誤差越小.而網(wǎng)格大小最主要的判定條件取決于入射粒子所走的距離長短,若網(wǎng)格過大,每個時間網(wǎng)格(步長)所通過的路程則有可能在一兩個網(wǎng)格內,由此會導致巨大的誤差.根據(jù)上述的誤差來源,需要考慮兩個條件： 一是時間網(wǎng)格大小即時間步長,二是氘氚等離子體熱運動的速率.根據(jù)公式

計算所走路程L,以此推出合適的網(wǎng)格大小設置.

對于慣性約束核聚變裝置,如美國國家點火裝置,其實際發(fā)生核反應的時間大約在10－10－10－11s.根據(jù)流體力學中判斷計算收斂的柯朗?弗里德里奇?列維條件,計算并設定時間步長為t=1 ns.

對于氘氚等離子體熱運動速率,應以模擬中的最小速率為下限,選擇模擬所設定的最小溫度的最概然速率作為估算網(wǎng)格速率的參考速率值,則有

其中,vm為T溫度下麥克斯韋速率分布的最概然速率.根據(jù)(9)式計算,等離子體溫度為20 keV時,氘粒子入射,其最概然速率為1.9575 × 106m/s;氚粒子入射,其最概然速率為1.1325 × 106m/s.估算時,只考慮這個速率的數(shù)量級106,由(8)式可得

即,入射粒子云所走的路徑長度在10－3m量級以上,為保證10%以下的誤差,網(wǎng)格大小應至少在10－4m以下,故設定網(wǎng)格大小為10－4m.

2.3 不同反應類型截面修正

本文所用數(shù)據(jù)來自ENDF/B?VI和ENDF/B?VII的氘氚聚變反應數(shù)據(jù)庫,其數(shù)據(jù)由美國洛斯阿拉莫斯國家實驗室(LANL)利用EDA?R矩陣碼對氘氚聚變反應進行研究所生成的評價中子數(shù)據(jù).其中,D?T的反應數(shù)據(jù)是ENDF/B?VI和ENDF/B?VII的官方原數(shù)據(jù),D?D的反應數(shù)據(jù)是洛斯阿拉莫斯國家實驗室的一個初步結果,有ENDF格式、HTML格式和PDF格式三種[17].

本文模擬的是氘氚等離子體聚變反應的中子產(chǎn)生率,只需要考慮3個反應,分別是

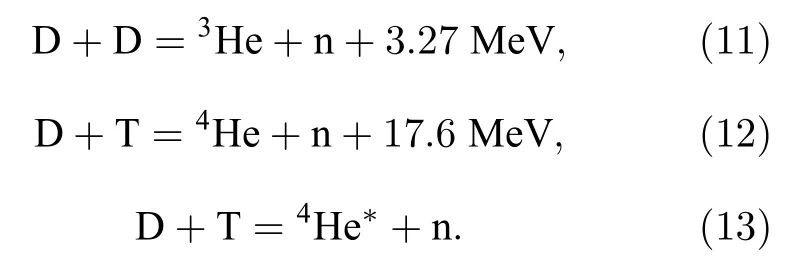
對于給定溫度,氘氚等離子體在滿足麥克斯韋速率分布的條件下,在任何速度、任何角度的位置上都存在粒子,因此在進行截面修正時,應同時考慮這兩個物理量對微分截面的影響.本文修正截面的目的在于解決大數(shù)據(jù)量模擬計算時計算空間不足的問題,將所有滿足同一麥克斯韋速率分布的粒子的截面歸一化為一個截面值,即當粒子數(shù)量足夠多時,無論入射粒子與靶粒子的夾角有多大,靶粒子的速率大小有多大,可使用同一微分截面值.

按照麥克斯韋速率分布函數(shù)的概率做離散化處理,即

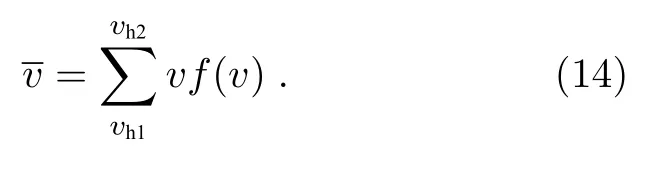
由于不需要考慮出射后的動量方向,所以只需要將入射粒子和靶粒子的動量矢量夾角進行歸一化,即仰角歸一化.同時,當仰角確定時,整個方向角的圓周上,都應有粒子存在,所以每一仰角所占概率,應為仰角所對應的球帶占整個球表面積的比例,如圖4所示.

其概率為

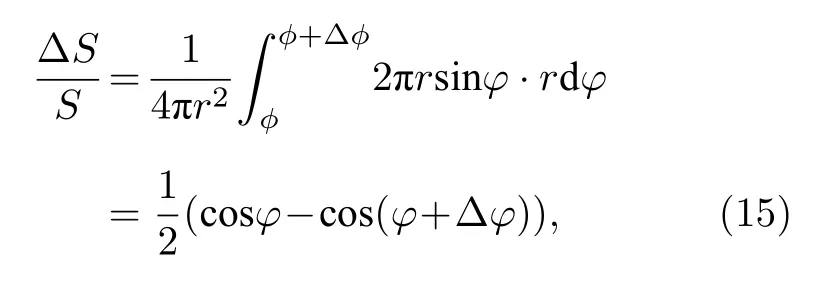
圖4 仰角對應球帶(球坐標)Fig.4.Elevation corresponding to the ball belt (ball co?ordinate).

其中,?為仰角,??為離散化的角度間隔.則歸一化的仰角為

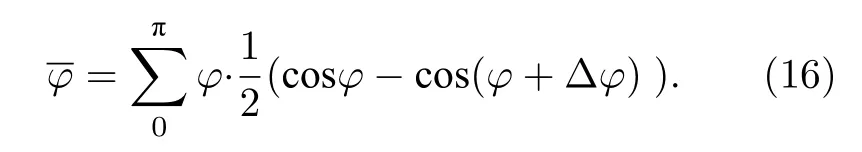
對于D?D,D?T,T?D反應截面,首先計算出某一溫度下粒子能夠具有的速率區(qū)間[vh1,vh2],計算入射粒子動量P1和靶粒子動量P2,計算速率所對應的麥克斯韋速率分布概率f.以仰角為循環(huán)變量,從0到π,計算碰撞后的動量P,以之計算質心系能量,并計算仰角對應的概率 ΔS/S.得到質心系能量后,從數(shù)據(jù)庫中讀取對應截面σ,利用公式

計算出修正后的截面值,獲得對應不同入射粒子能量的矩陣.

2.4 路徑函數(shù)與隨機函數(shù)設計

本文所模擬的等離子體只包含氘離子和氚粒子,且認為這些粒子均勻分布.因為氘氚聚變反應率需要通過路徑長度計算,因此計算入射粒子云的運動路徑(路徑函數(shù))較為關鍵.這里對路徑函數(shù)做一簡要說明： 首先輸入入射粒子云的初始位置(x,y,z)和入射粒子云速率的三個坐標分量(vx,vy,vz).然后建立一個n× 3的矩陣,其中n代表著入射粒子云走過的網(wǎng)格數(shù),3即為三個坐標值.為避免漏算網(wǎng)格導致誤差,將原時間步長1 ns細分成時間網(wǎng)格10－12s,計算每一個時間網(wǎng)格內入射粒子云走過的網(wǎng)格數(shù),進而計算路徑長度.

本文中,除等離子體溫度和氘氚粒子數(shù)密度已知外,對于氘氚粒子云的位置、速率、方向等均隨機產(chǎn)生.本文采用了全部隨機方法,即無論是入射粒子云的種類、位置,或是速率,還是方向,均按照一定概率進行隨機抽樣.由于入射粒子云不同,對應的麥克斯韋速率分布并不完全相同,所以要先判斷是哪種粒子,分兩種情況進行后續(xù)的部分.對于入射氘粒子云,先求出氘粒子云在此溫度下的最概然速率vm,并求出兩個半高寬的速率范圍[vh1,vh2],然后求解麥克斯韋速率分布函數(shù),離散化后利用函數(shù)依概率進行隨機,得到一個速率值.對極角也做同樣的離散化處理.對于入射氚粒子云,與氚粒子云入射算法相同,更改質量參數(shù)即可.

2.5 算法流程圖

總的算法流程見圖5.

3 氘氚聚變反應模擬分析

3.1 初始邊界條件

為與解析公式(1)進行比較,本文中,ni=1014cm－3,氘氚粒子各占50%,并滿足勞森判據(jù).慣性約束等離子體時間步長通常在納秒量級[18],因此本文設置時間步長為1 ns.根據(jù)2.2節(jié)的工作,設定網(wǎng)格大小為10－4m.模擬的溫度取值為20,40,60,80,100 keV.為確保精確度,對于每一個所模擬的溫度,粒子云速率離散為1000個網(wǎng)格,極角離散為180個網(wǎng)格,方位角離散為360個網(wǎng)格.采用MC方法對105個網(wǎng)格單元進行采樣,采樣網(wǎng)格單元作為入射粒子云網(wǎng)格來控制統(tǒng)計誤差.

3.2 模擬結果與討論

三種聚變反應截面的溫度修正結果如圖6所示(1 barn=10－24cm2).

從圖6(b)和圖6(c)可明顯地看到多普勒效應.這是由于氘氚等離子體中,靶粒子服從麥克斯韋速率分布,因此在截面溫度修正后,能量將有所展寬,且溫度越高,麥克斯韋速率分布范圍越寬,由此靶粒子展寬越大,同時峰值截面也逐漸減小.經(jīng)截面修正,將所有滿足同一麥克斯韋速率分布的粒子的截面歸一化為一個截面值,解決了大量靶粒子熱運動所帶來的大數(shù)據(jù)量模擬計算時計算空間不足的問題,大大節(jié)約了計算時間.

氘氚等離子體聚變反應模擬結果如圖7所示.

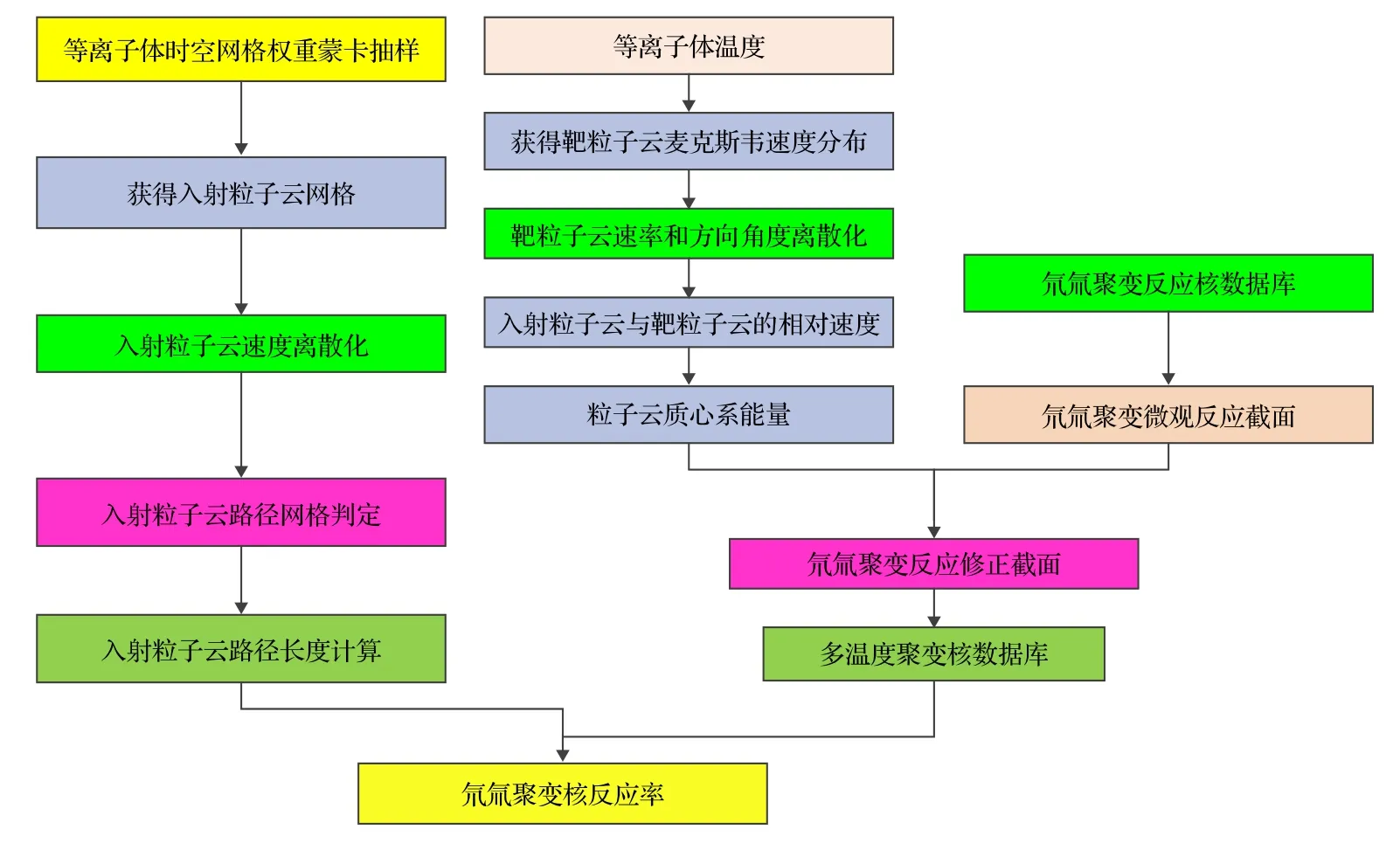
圖5 氘氚等離子體聚變反應模擬流程圖Fig.5.Simulation flow of deuterium?tritium plasma fusion reaction.

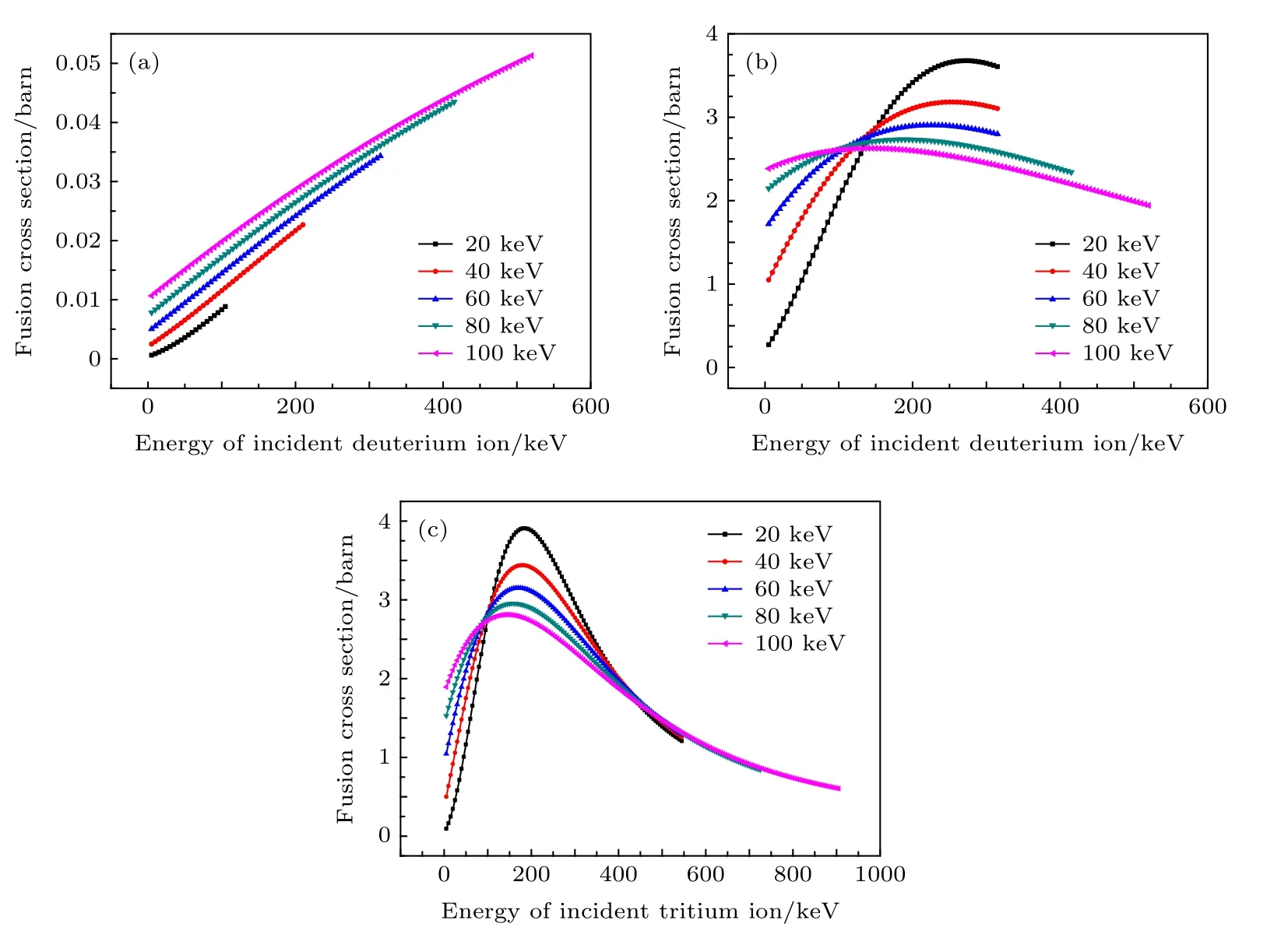
圖6 氘氚等離子體聚變反應修正 (a) D?D反應截面修正;(b) D?T反應截面修正;(c) T?D反應截面修正Fig.6.Correction of fusion reaction of deuterium?tritium plasma： (a) D?D fusion cross section correction;(b) D?T fusion cross sec?tion correction;(c) T?D fusion cross section correction.

從圖7可以看出,根據(jù)解析公式法,隨等離子體溫度的上升,中子產(chǎn)生率首先增加,在60 keV左右達到峰值,而后開始降低;而數(shù)值模擬結果則是中子產(chǎn)生率隨等離子體溫度上升而一直增加.根據(jù)三種聚變反應截面的溫度修正即圖6,分析可知氘?氘反應、氘?氚反應、氚?氘反應的截面在20－100 keV的范圍內呈遞增趨勢,在此范圍內,本文采用的數(shù)值模擬法相較傳統(tǒng)解析公式法,更符合ENDF/B?VI和ENDF/B?VII的氘氚聚變反應數(shù)據(jù)庫的截面數(shù)據(jù)趨勢.

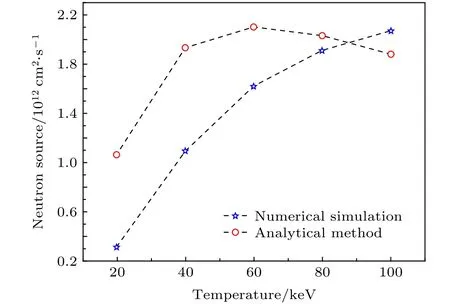
圖7 氘氚等離子體聚變反應中子產(chǎn)生率Fig.7.Neutron production rate of deuterium?tritium plasma fusion reaction.

下面分析等離子體處于低溫時數(shù)值模擬結果與解析公式法結果誤差過大的原因.首先,對于氘氚聚變反應率,解析公式法和本文采用了不同的計算方法,具體可參見本文第2節(jié)所述.另一方面,解析方法所用截面來自核物理分析方法,本文則采用了最新的ENDF核數(shù)據(jù)庫.根據(jù)圖7,解析方法所用的D?T聚變截面(聚變反應最重要的過程)在60 keV左右達到峰值,所獲得的中子產(chǎn)生率也在60 keV左右達到峰值.而本文所用數(shù)值模擬方法所獲得的中子產(chǎn)生率和ENDF/B?VII數(shù)據(jù)庫的聚變截面則在20－100 keV的范圍內呈遞增趨勢.兩種方法相比,在約20 keV,本文方法給出的聚變反應率遠低于解析方法,差異約70%.圖8對比分析了兩種方法所對應的聚變反應截面.根據(jù)該圖,D?T聚變截面在低于60 keV的范圍內出現(xiàn)明顯差異.就20 keV而言,解析法使用截面為0.4077 barn,本文方法使用截面為0.0597 barn,差異約85%.這可能是導致這兩種方法之間出現(xiàn)顯著差異的根本原因.

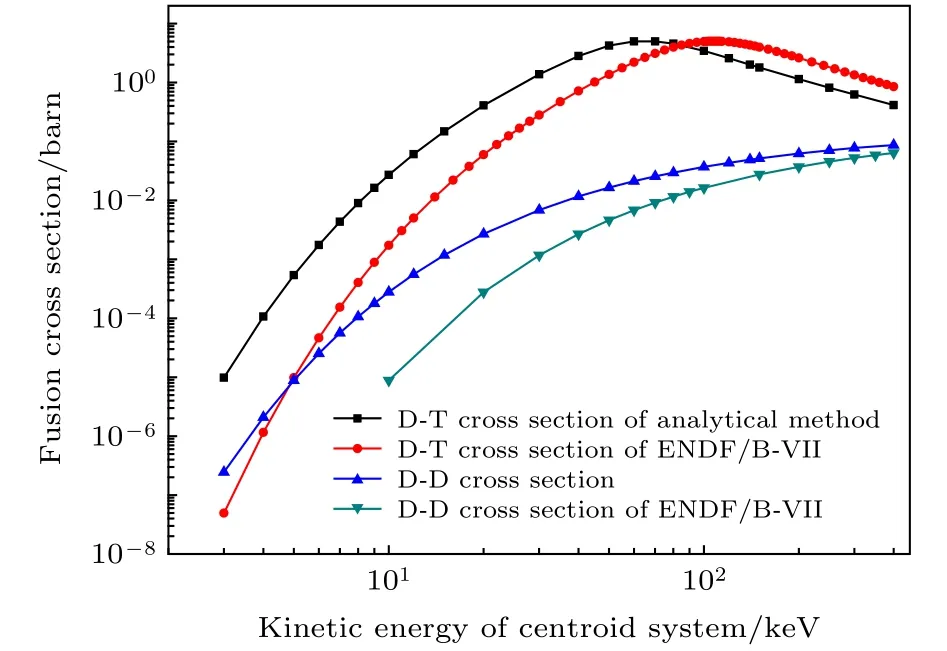
圖8 兩種方法聚變反應截面對比[19,20]Fig.8.Comparison of fusion cross sections of the two meth?ods[19,20].

4 結 論

本文針對慣性約束的激光等離子體,采用MC方法和SN方法,開展了D?T粒子云團聚變反應率的數(shù)值模擬工作.得到以下結論： 1)與原核數(shù)據(jù)庫截面相比,D?T,D?D,T?D截面經(jīng)修正后多普勒溫度效應顯著;2)在等離子體溫度20－100 keV范圍內,本文數(shù)值模擬結果較解析公式法更符合ENDF/B?VI和ENDF/B?VII的氘氚聚變反應數(shù)據(jù)庫的截面數(shù)據(jù);3)本文數(shù)值模擬結果與與解析公式法結果在低能區(qū)存在較大誤差,可能是計算方法不同與低溫截面差異過大原因導致.