混流式水輪機轉輪模態計算及振動特性分析

史廣泰，楊 茜，劉宗庫，薛志成

(1.西華大學流體及動力機械教育部重點實驗室，四川 成都 610039；2.西華大學能源與動力工程學院，四川 成都 610039)

作為一種極為重要的旋轉機械，水輪機的安全可靠運行直接影響企業效益和經濟發展[1]。但近年來通過分析水電站運行資料發現，水輪機轉輪經常產生疲勞破壞，甚至斷裂，這成為水輪機組運行及我國水電事業發展的潛在威脅，同時也成為業內人士關注的重點。多年來許多學者對此進行研究，并取得了顯著的成效。劉德民等[2]采用流固耦合方法對某混流式水輪機進行振動分析，并比較了流量和離心力對轉輪模態的影響。岳志偉等[3]基于ANSYS有限元計算平臺利用流固耦合理論對可逆式水輪機轉輪進行干、濕模態分析，結果表明轉輪葉片的最大變形出現在葉片出水邊中部。梁權偉等[4]利用順序流固耦合的方法對混流式水輪機轉輪進行強度和模態分析，并與實際發生疲勞位置相對比，結果表明轉輪發生疲勞原因不是靜應力而是動載荷。呂桂萍等[5]通過對混流式水輪機轉輪固有頻率進行分析，得到了水輪機發生共振的影響因素。廖偉麗等[6]運用有限元分析方法對混流式水輪機轉輪以及整體進行模態分析，得到了水輪機轉輪單葉片和整體固有頻率，分析水輪機過流部件水力激振頻率與水輪機機組共振頻率之間的關系。除了上述文獻外，其他一些學者也對水輪機轉輪進行了相關研究，并得到了顯著成果[7-11]。

水輪機在運轉過程中受到自身重力、旋轉慣性力和水力不穩定性的影響，其應力應變情況非常復雜，故本文針對國內某電站水輪機轉輪葉片表面出現的裂紋、斷裂的具體情況，在總結前人研究成果的基礎上，應用流固耦合理論對水輪機轉輪進行模態分析，進而總結其變形及振動特性。

1 數值計算方法

1.1 標準k-ε模型

本文采用標準的k-ε湍流模型，其方程如下：

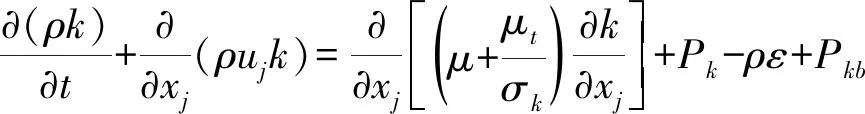
(1)

式中：k、ε分別是湍動能和湍流耗散率；μt為湍流黏性系數；模型常數Cε1=1.44，Cε2=1.92，σε=1.3，σk=1.3。

1.2 固體彈性結構有限元理論

對轉輪葉片模態分析得到的轉輪葉片動應力主要是由低頻組成的，因此本文在數值計算過程中，結構瞬態響應求解采用Ansys有限元提供的隱式求解法Newmark時間積分法，具體方程如下：

(2)

(3)

(4)

(5)

式中，ut+Δt可由t+Δt時刻的運動方程求得，即

(6)

當γ≥0.5、β≥0.25(γ+0.5)2時，Newmark法無條件穩定，即數值計算的過程中，解的穩定性不受時間步長大小的影響。

2 研究對象及模型建立

本文研究對象為混流式水輪機，其型式為：HLD307-LJ-290。基本參數為：額定出力，92.3 MW；最大出力，107 MW；最大水頭，184 m；額定水頭，159.3 m；額定流量，62.7 m3/s；額定轉速，272.7 r/min；最大吸出高度，-3 m。

首先利用Unigraphics NX的幾何建模功能，建立本水輪機的三維幾何模型，如圖1所示為水輪機的三維水體幾何模型。

3 網格劃分及邊界條件設置

由于水輪機各過流部件結構復雜，而且轉輪葉片為三維扭曲曲面，形狀不規則，因此采用適應性較強的非結構網格對流體域及轉輪實體進行網格劃分，并對關注的區域網格進行局部加密。這樣既能保證網格的生成速度和后續計算的準確性，也可提高計算效率。經過網格無關性驗證后，最終確定的計算域網格數為500萬左右，其中轉輪實體的網格數為60萬左右，網格劃分如圖2所示。

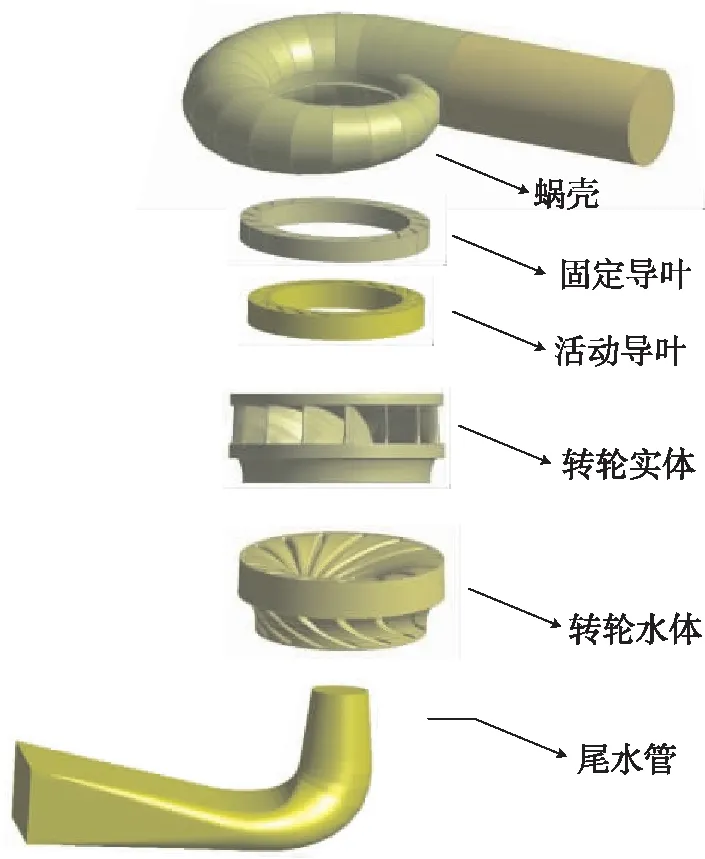
圖1 水輪機三維幾何模型

圖2 水輪機過流部件網格劃分

網格劃分完成后，運用Ansys Workbench 平臺對水輪機全流道進行數值模擬。其邊界條件設置如下：水輪機蝸殼進口和尾水管出口分別設為總壓進口和靜壓出口。另外，活動導葉和轉輪進口交界面設置為動靜交界面，壁面選用無滑移壁面，參考壓力為一個大氣壓。

在進行流固耦合計算時，轉輪上冠軸承處設置固定約束并考慮離心力的作用，并將轉輪流體域受到的壓力加載到轉輪實體上。

4 轉輪模態振動分析

4.1 固有頻率分析

表1為在額定水頭3種典型開度(40%、70%和100%)下轉輪在水中的固有頻率。

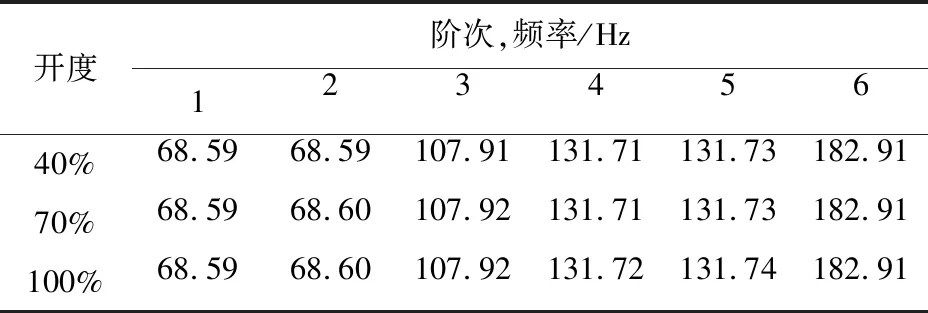
表1 不同工況下轉輪在水中的固有頻率

由表1可知：不同工況對應相同的階次轉輪的固有頻率相差很小，因此本文后續選取100%一種工況進行模態和振動分析。

表2為在100%開度工況下轉輪自由模態和預應力模態的固有頻率。由表2可知：在有預應力的情況下頂蓋的固有頻率比自由模態情況下顯著降低，各階頻率變化率均高于34%，因此預應力對轉輪模態分析影響很大，在轉輪的模態分析中不可忽視其影響。

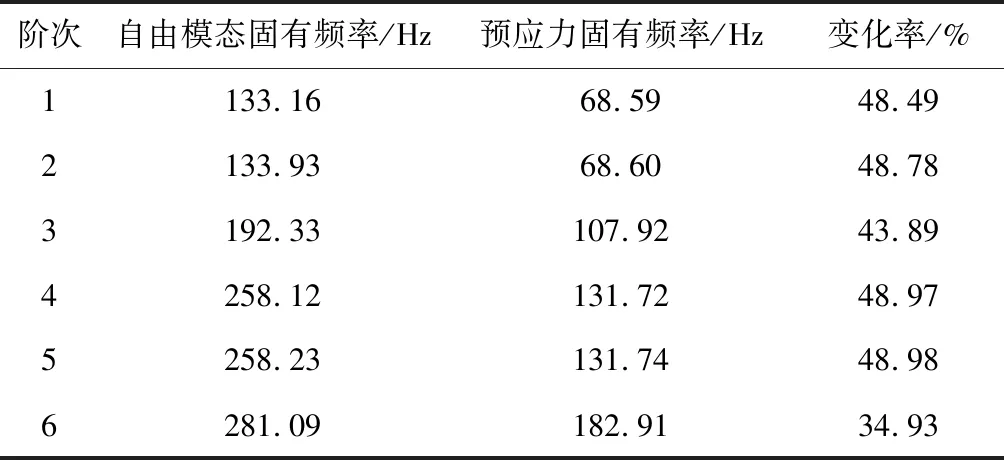
表2 轉輪自由模態和有預應力下的固有頻率

4.2 轉輪振型分析

考慮到機組的實際運行情況以及文章篇幅，本文選取額定水頭100%開度工況進行后續分析。

圖3為轉輪自由模態的前6階振型圖。由圖3可知，轉輪的第1、2階振型相似，主要表現為彎曲變形。在上冠軸孔附近變形量較小，并且最小變形區域呈對稱分布，而最大變形量出現在葉片出水邊靠近下環處。另外還發現下環變形量略大于上冠。

轉輪的第3階振型主要表現為繞軸旋轉。從變形量分析，轉輪變形量繞旋轉軸對稱性較好，最大變形量出現在葉片出水邊靠近泄水錐處，而最小變形量則出現在葉片進水邊中部，上冠變形量由軸孔向外逐漸增大。

轉輪的第4、5階振型相似，主要表現為泄水錐的左右擺動和葉片的彎曲變形。最大變形量出現在葉片出水邊，最小變形量出現在葉片進水邊中部。

轉輪的第6階振型主要表現為下環和葉片的局部彎曲變形。下環變形成為了三角形，上冠和下環的相對位置基本保持不變。葉片表現為非常明顯的扭轉。轉輪上冠和泄水錐處變形較小，最大變形量仍然出現在葉片出水邊。

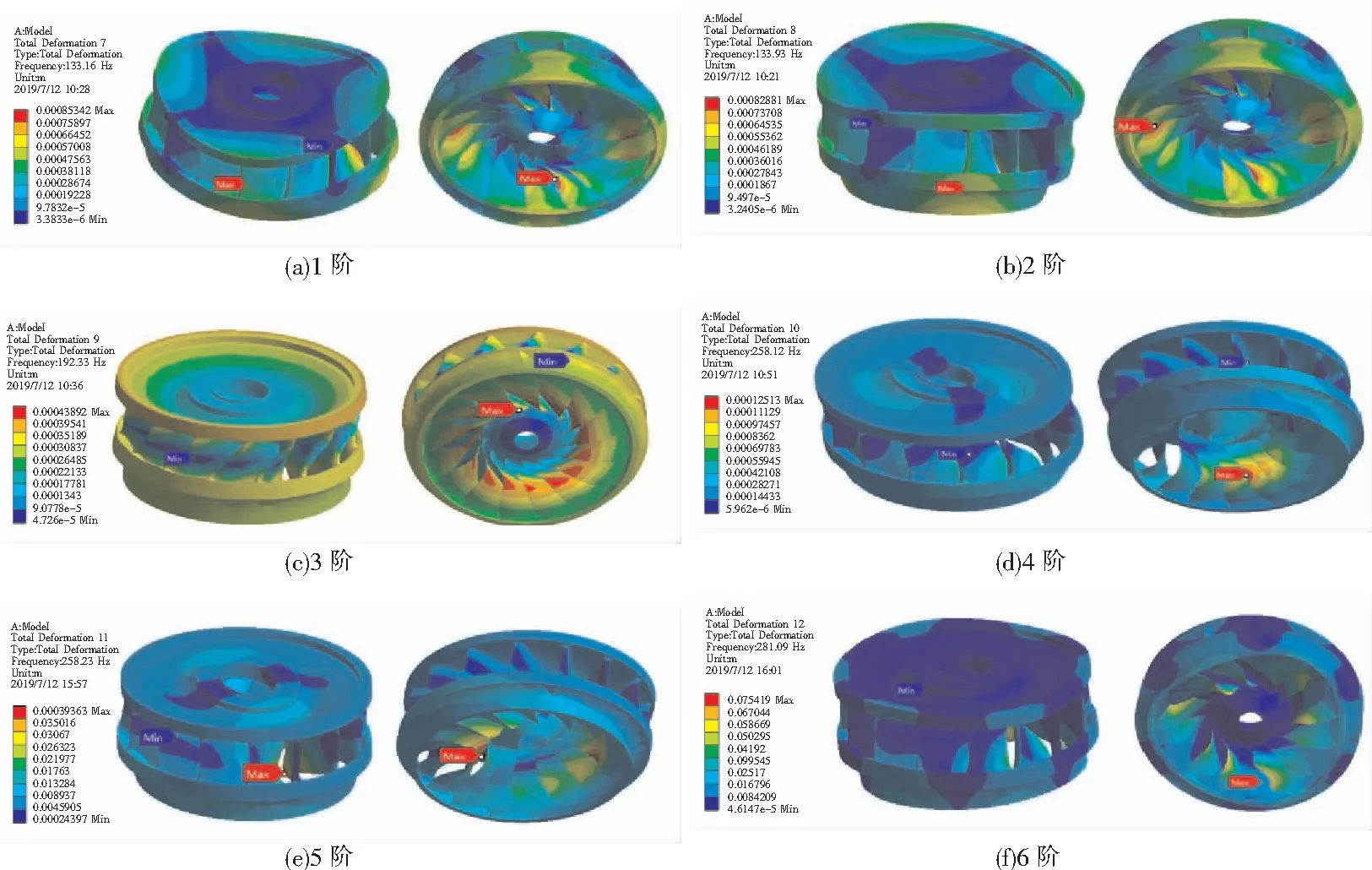
圖3 水輪機轉輪自由模態前6階振型

當振動頻率較低時，振動形式是以轉輪的整體振動為主導，但是隨著頻率的不斷升高，轉輪的振動形式逐漸變為以局部振動為主導。

圖4為水輪機轉輪預應力模態下的振型圖。

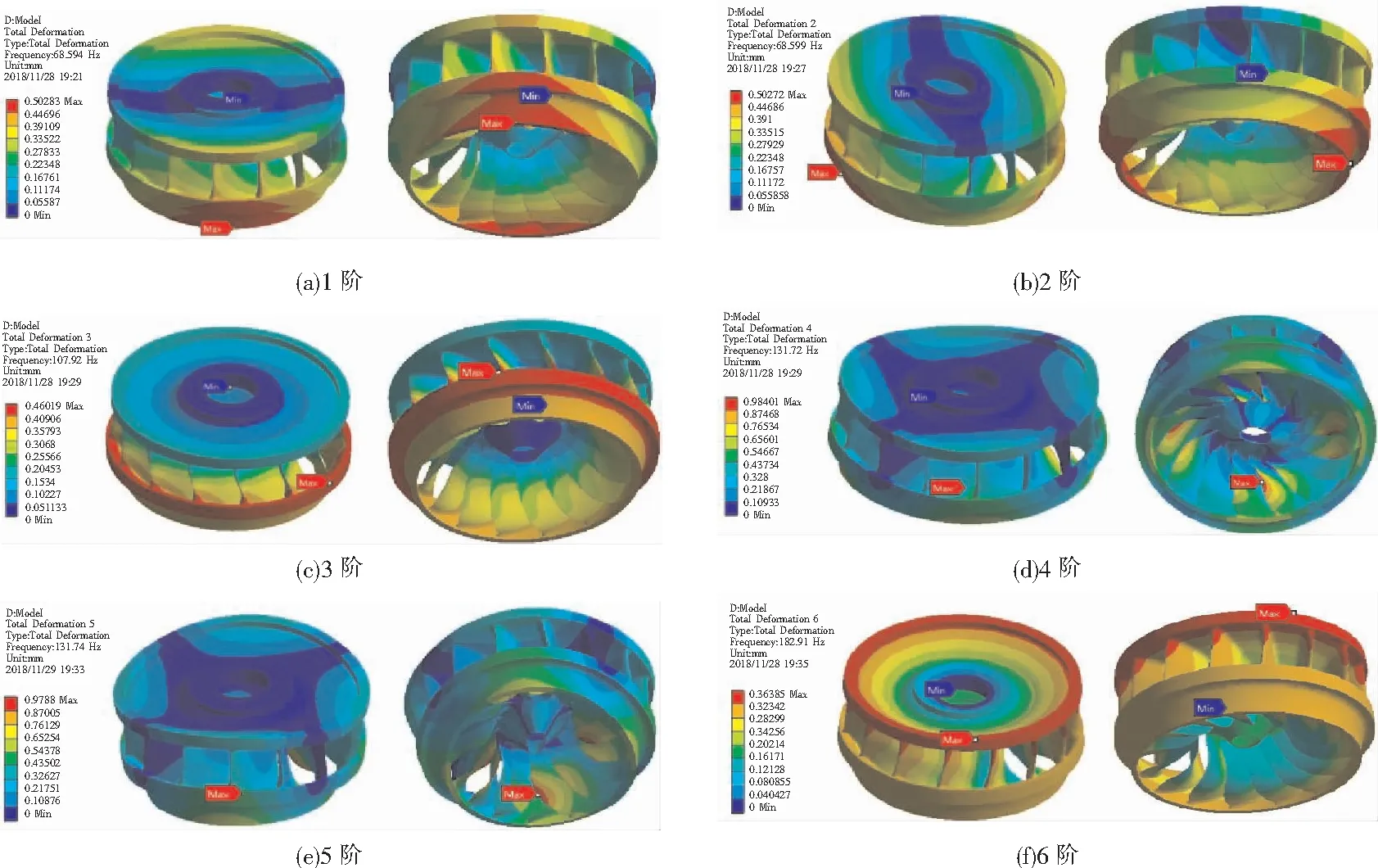
圖4 轉輪各階固有頻率對應的振型圖

由圖4可知，轉輪第1、2階振型主要表現為類似于鐘擺的整體擺動，最大和最小變形分別出現在上冠和下環處，在葉片出水邊變形量沿著泄水錐到下環方向逐漸增大。

轉輪的第3階振型主要表現為繞軸的旋轉運動，轉輪上冠處變形量從軸孔到外緣逐漸增加且在軸孔以及泄水錐附近變形量最小，在下環以及下環靠近葉片進水邊處的形變量相對較大。另外發現葉片出水邊靠近下環變形量明顯較大。

轉輪的第4、5階振型主要表現為彎曲變形，其振型圖相似。上冠最小變形區域和葉片出水邊最大變形區域繞軸對稱分布，轉輪整體變形不均勻程度較大。

轉輪的第6階振型主要表現為轉輪上冠沿軸向方向上下振動，轉輪下環的變形量相比上冠來說較小。另外，還發現葉片出水邊變形較為均勻，而在葉片進水邊處變形梯度較大。

由上述分析可知水輪機轉輪振動形式主要有4種，分別為擺動、繞軸旋轉、彎曲變形及沿軸向方向上下振動。同時發現，頻率相近的低階振型具有一定的對稱性。這主要是由于轉輪結構和周圍約束具有對稱性所致。1階、2階、3階及6階頻率下的振動以轉輪的整體振動為主，而4階及5階頻率下的振動以局部振動為主。另外，由于固定約束施加在上冠軸孔處，所以上冠形變小，同時轉輪的最大變形主要集中在轉輪上冠和下環以及進出水邊局部位置的葉片出水邊和下環處。圖5為轉輪實際變形位置。由圖可知在葉片出水邊靠近泄水錐附近產生裂紋，而在葉片出水邊靠近下環處發生斷裂。這是由于葉片根部應力過大所致。

圖5 轉輪實際發生破壞的位置

4.3 轉輪振動特性分析

4.3.1 典型激振力頻率的計算

1)導葉出口水流引發的脈動。

導葉出口的不均勻流動會對轉輪產生一定程度的擾動，其作用于轉輪上的水流擾動頻率可以通過下式計算得出：

(7)

式中：n為水力機組的轉速；zg為活動導葉的個數。由式(7)可以得到在計算工況下(n=272.7 r/min)的活動導葉出口水流引發的脈動頻率為109.08 Hz。

2)葉片的旋轉頻率。

水輪機轉輪葉片在旋轉的過程中，水流從葉片進口到出口，作用力隨轉頻周期性變化，其頻率可按下式計算：

(8)

式中：n為水力機組的轉速；z為轉輪的葉片個數。利用式(8)可以得到轉輪在計算工況下(n=272.7 r/min)的旋轉頻率為68.175 Hz。

4.3.2 轉輪固有頻率與典型激振力頻率的對比分析

轉輪的激振頻率如表3所示。通過對比表2和表3中數據可以看出：水輪機在轉速n=272.7 r/min下運行時，轉輪的第3階固有頻率與導葉出口水流引發的脈動頻率幾乎相等，可能會誘發轉輪共振，從而引起機組振動幅度急劇增加；而其他固有頻率與激振頻率相差較大，所以共振可能性較小。

表3 轉輪可能的激振頻率

5 結論

1)水輪機轉輪振動形式主要有4種，分別為擺動、繞軸旋轉、彎曲變形及沿軸向方向上下振動。同時發現預應力對轉輪模態分析影響很大，在轉輪的模態分析中不可忽視其影響。

2)在預應力模態分析中，第1階和第2階、第4階和第5階振型相似。另外，水輪機轉輪最大變形主要位于轉輪上冠、下環以及葉片出水邊中部。

3)水輪機在轉速n=272.7 r/min下運行時，轉輪的第3階固有頻率與導葉出口水流引發的脈動的頻率幾乎相等，可能會誘發轉輪共振。同時，發現在水輪機實際運行過程中，由于轉輪葉片根部應力過大而導致葉片斷裂。