多級壓裂裂縫誘導應力優化計算模型研究

祝銘辰

(中國石化華東油氣分公司泰州采油廠地質研究所，江蘇 泰州 225300)

大規模儲層改造需要在儲層中壓開多條裂縫，為了科學指導壓裂設計以及壓裂后評估，探索多級壓裂誘導應力的計算模型就顯得尤為重要[1-3]。現有多級壓裂裂縫誘導應力計算模型都是單一裂縫誘導應力的簡單疊加，本研究考慮裂縫間的相互影響，對多級壓裂各裂縫凈壓力值進行修正，從而建立多級壓裂裂縫的誘導應力計算模型。

1 單一垂直裂縫誘導應力計算模型

假設無限大儲層中存在有一條垂直的對稱雙翼裂縫(見圖1)，該裂縫可簡化為一條長為2h的直線狀裂紋(可以當做短半軸趨向于零的橢圓的極限情形)，裂紋穿透板厚，作用于裂紋面上的壓力為Pnet。

此問題屬于彈性力學范疇，需要聯立彈性力學的平衡微分方程、幾何方程及物理方程求解。西南石油大學根據彈性力學的半逆解法[4-5]求得圖1坐標系下的解析解為

(1)

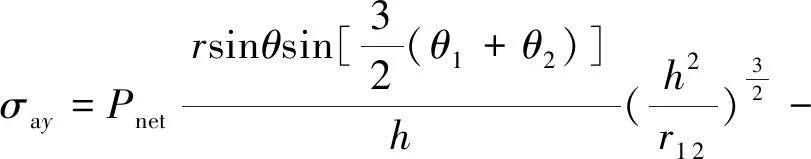
(2)

σax=υ(σay+σaz)

(3)

式中，σax、σay、σaz分別為x、y、z方向上的誘導應力，MPa；Pnet為裂縫凈壓力，MPa；h為裂縫半縫高，m；ν為儲層泊松比，無因次。

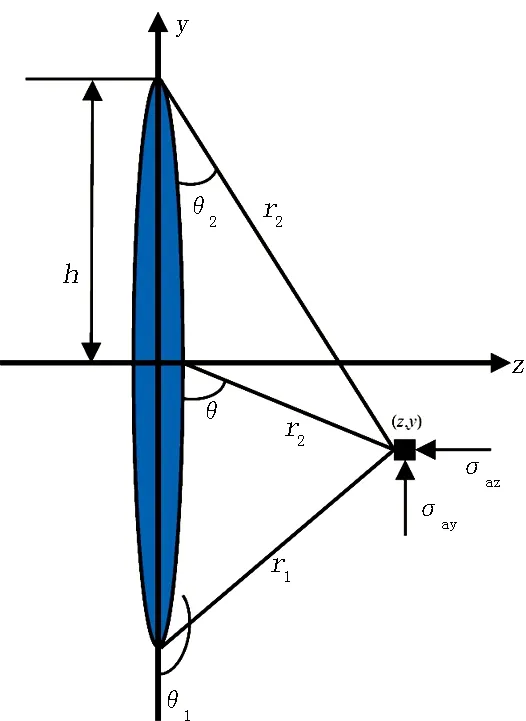
圖1 單一垂直裂縫誘導應力場

2 多級壓裂裂縫誘導應力計算模型

假設裂縫均為垂直且相互平行的裂縫，多級壓裂裂縫的物理模型可以簡化為圖2所示[6]。

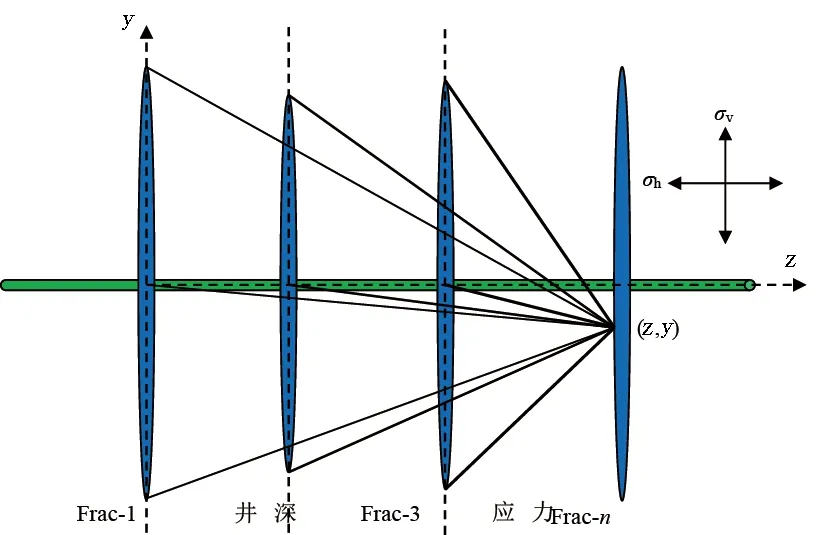
圖2 多級壓裂裂縫物理模型

取其中任意一條裂縫作為研究對象，該裂縫周圍垂直于裂縫面方向的地應力變為

σh′=σh∑σaz

(4)

式中，σh′為考慮誘導應力影響的主應力，MPa。

而凈壓力、水平最小主應力以及裂縫內液體壓力之間存在以下關系

σh+Pnet=PL

(5)

式中，PL為裂縫內液體壓力，MPa。

因此，裂縫壁面凈壓力會產生誘導應力改變地應力的大小，而改變的地應力同時又會反過來使裂縫的凈壓力發生改變。考慮地應力與凈壓力的相互作用，式(5)可以寫成

σh′=Tnet=PL

(6)

在一定的時間內我們可以認為裂縫內的液體壓力是不變的，因此聯立式(5)和式(6)并將式(4)帶入，可得

∑σaz+Tnet=Pnet

(7)

式中，Tnet為修正后的凈壓力，MPa。

令

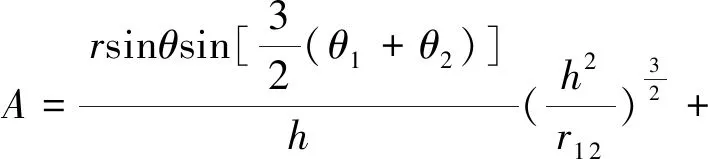
(8)

則式(1)可簡化為

σaz=-Pnet1A

(9)

考慮如圖2所示的裂縫系統，設n條裂縫的原始凈壓力分別為Pnet1、Pnet2、……Pnetn，n條裂縫的修正凈壓力分別為Tnet1、Tnet2、……Tnetn，Aij為第Frac-i對Frac-j產生誘導應力的系數。根據式(7)所示的平衡條件，可以列出矩陣方程為

(10)

使用迭代法解矩陣方程即可以得到各條裂縫的修正凈壓力值，再根據疊加原理，多級壓裂裂縫誘導應力計算模型。

圖3 多級壓裂裂縫誘導應力分布

根據二維垂直單縫誘導應力計算，可得第n條水力裂縫在z-y平面內誘導應力大小為：

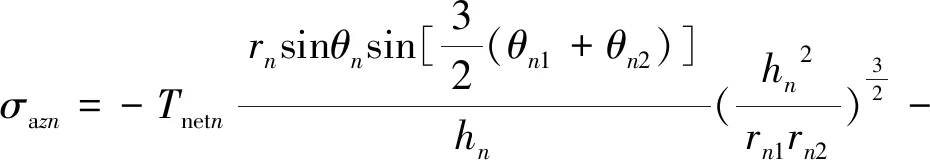
(11)

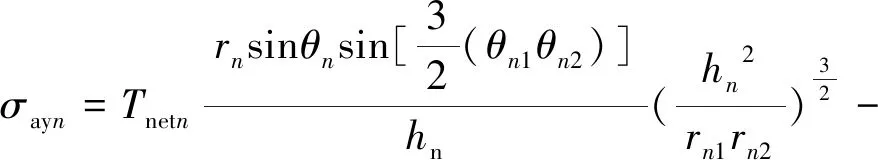
(12)

σaxn=υ(σayn+σazn)

(13)

式中，σaxn、σayn和σazn為先壓開第n條裂縫產生的誘導應力的正應力分量，MPa；Tnetn為第n條裂縫修正凈壓力，MPa。

根據矢量的疊加原理，先壓的n條裂縫在點(z,y)處產生的誘導應力的總和可以表示為：

(14)

3 與有限元方法計算結果對比

假設地層中存在兩條平行裂縫，兩條裂縫縫高為60 m，壁面凈壓力為15 MPa，相距100 m，地層的泊松比為0.32。根據圣維南定理[7-8]，當地層尺寸超過裂縫尺寸的6～7倍之后，可以忽略邊界對所研究區域應力分布的影響。因此，選取地層大小為邊長600 m的正方形。利用COMSOL軟件，建立起的有限元模型及求解結果見圖4。

圖4 有限元模型及計算結果

兩條裂縫在最小水平主應力上的誘導應力大小的模擬結果，計算結果及未修正公式計算結果見圖5。

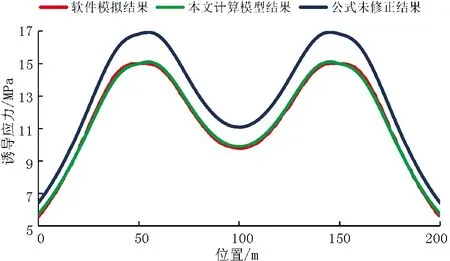
圖5 結果對比

從圖5中很明顯可以看出，使用軟件模擬的結果與本文中對各裂縫壁面凈壓力進行優化的公式計算結果較為吻合，而未修正公式的計算結果則與其余兩種方法的計算結果有較大的偏差。從而可以說明修正公式的計算具有較高的正確性。

4 計算結果與微地震監測數據對比

水平井分段多級壓裂實現了儲層在長、寬、高方向上的立體改造。現場常規的監測裂縫改造區域的方法是微地震監測法，然而由于其成本較高，不可能保證每一口大型壓裂井都進行微地震監測工作。顯然，如果裂縫發生了轉向就有可能使縫網向垂直于主裂縫的方向擴展，增加改造范圍。本節通過使用優化的多級壓裂裂縫誘導應力的計算模型，計算了P1井裂縫的轉向區域，評價裂縫的改造范圍，并與微地震監測數據對比，以驗證模型的準確性。

4.1 誘導應力對地應力場的影響

在考慮壓裂人工裂縫誘導應力影響下，地應力場可以看成是由原地應力場和水力裂縫的誘導應力場疊加，如圖6所示。

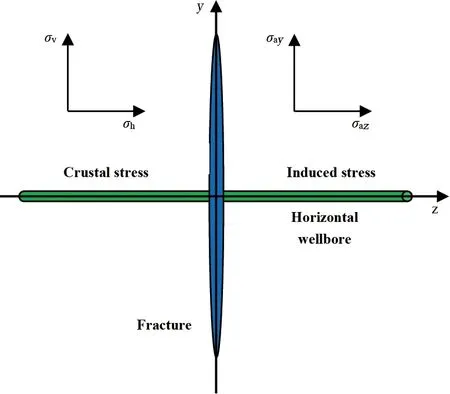
圖6 水力裂縫形成后的應力場

據疊加原理，初始裂縫產生后井筒周圍的復合地應力場為：

(15)

式中，σv′、σH′、σh′為垂向、最大和最小水平主應力方向上的復合應力，MPa；

σay、σax、σaz為垂向、水平最大主應力和水平最小主應力方向上的誘導應力，MPa。

4.2 裂縫的轉向條件

水力壓裂裂縫總是垂直于最小主應力的方向延伸，當最小水平主應力和最大水平主應力方向發生反轉時，則可以認為裂縫發生了轉向，即轉向條件為

σH′<σh′

(16)

水平井多級壓裂過程中，第一級壓裂之前由于井筒周圍原地應力方向并沒有改變，因此第一級壓裂的主裂縫方向是垂直于最小水平主應力的方向的。在之后的壓裂過程中，由于地層中已經存在了壓裂裂縫，因此會在原始水平地應力上附加一個由前幾級壓裂裂縫產生的誘導應力，在這種情況下，水平地應力就可能發生改變。同樣的情況，當前壓裂裂縫也會對地應力產生影響。

將公式(15)代入式(16)得

σH+σax<σaz-σax

(17)

從式(18)可以看出，當原始水平地應力差小于誘導應力差時，裂縫即達到了轉向條件。

4.3 P1井計算結果實例

P1井是致密砂巖中一口分段壓裂水平井，共分16段進行壓裂，為計算壓裂的橫向改造范圍，對壓裂過程進行了如下適當的簡化：

(1)每一簇射孔孔眼處都能產生一條主裂縫；

(2)各級壓裂時，每一簇射孔孔眼處的主裂縫同時形成；

(3)主裂縫延伸至最大縫高之后才開始形成縫網。

對P1井各段進行計算，很明顯當垂直于壓裂主裂縫上的某處的壓裂時的誘導應力差大于原始的地應力差時，則該區域屬于被改造的范圍。其中第十二級的計算結果如圖7所示。

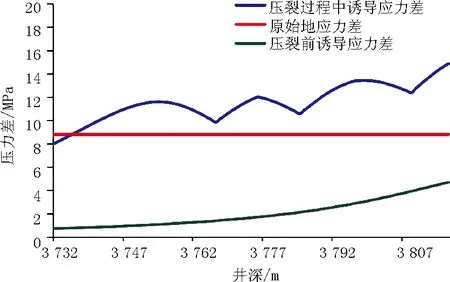
圖7 第十二級壓裂誘導應力差計算結果

藍色線在紅色線以上的部分即為壓裂在沿著井眼方向的改造范圍，對全井進行計算，結果見表1。

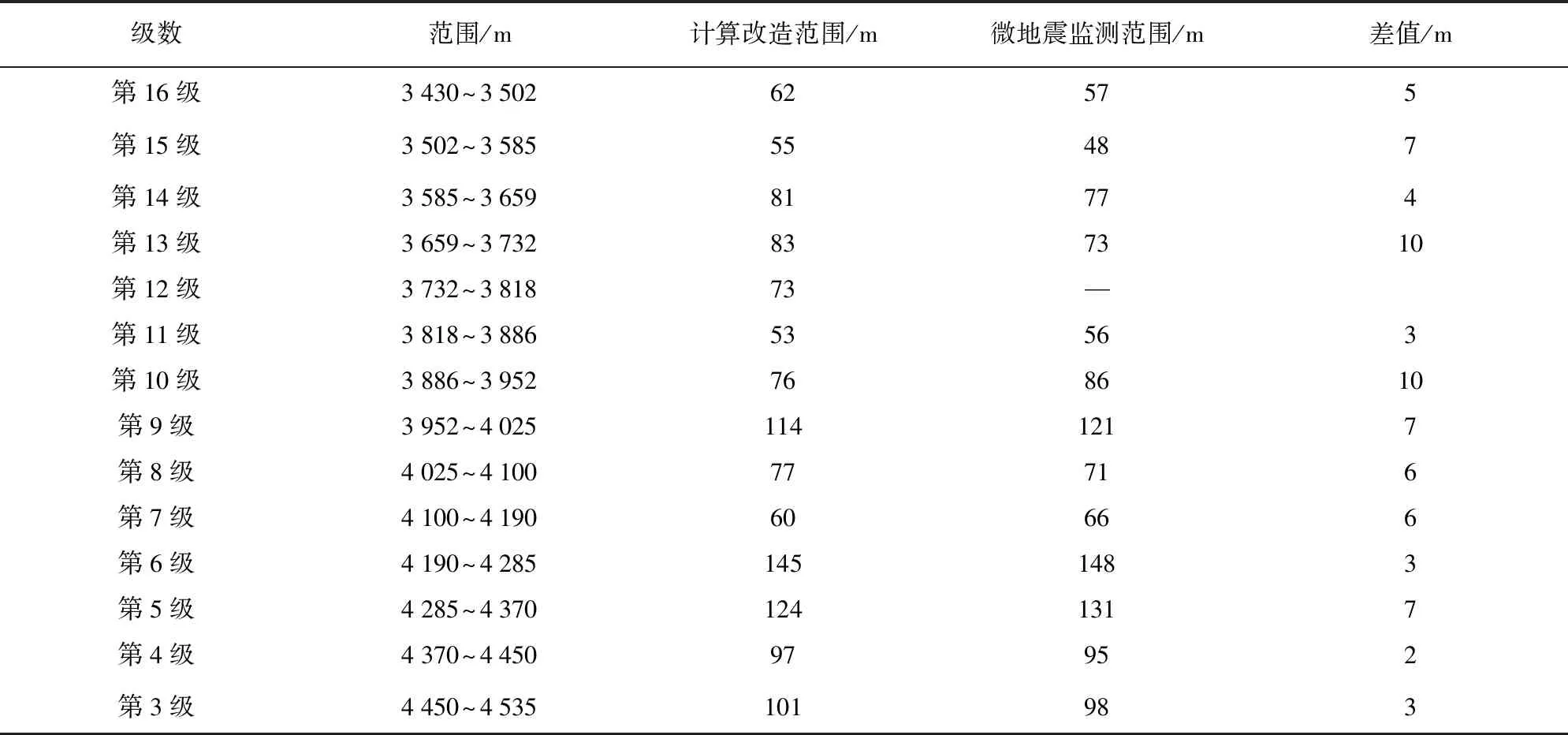
表1 計算結果與監測結果對比

可見計算數據與微地震數據吻合較好，說明優化后的誘導應力計算模型有較高的現場應用價值。

5 結論

(1)多級壓裂裂縫引起的誘導應力不能看作各裂縫所引起誘導應力的簡單疊加，應該考慮裂縫之間的相互影響。裂縫凈壓力引起的誘導應力會改變地應力，從而又會影響裂縫的凈壓力。據此，可以對各條裂縫的凈壓力進行修正。得到每條裂縫的凈壓力之后根據疊加原理可以求得誘導應力分布。

(2)修正模型的計算結果與COMSOL有限元軟件模擬結果吻合較好，精度較未修正模型有明顯提高。

(3)以P1井為例使用修正模型計算出的結果與微地震監測結果吻合較好。

(4)多級壓裂裂縫誘導應力修正模型的建立為今后多級壓裂的設計與優化以及評價壓裂裂縫形態提供了理論依據。