體表形態凸角對腰圍間隙量的影響

應 欣， 程碧蓮， 劉 正,2,3， 鄒奉元,2,3

(1. 浙江理工大學 服裝學院， 浙江 杭州 310018； 2. 絲綢文化傳承與產品設計數字化技術文化和旅游部重點實驗室, 浙江 杭州 310018； 3. 浙江省服裝工程技術研究中心， 浙江 杭州 310018)

間隙量是指著裝狀態下服裝與人體表面的空隙部分，是影響服裝合體性、舒適性和三維虛擬試衣質量的關鍵因素[1],服裝合體性是人們選購服裝最關注的問題[2]。服裝個性化版型設計的本質是根據款式特點將人體形態信息和松量組合成為合體的著裝空間形態，因此，間隙量分布對版型設計與修改起著關鍵的指導作用。

目前，國內外學者針對人體與服裝之間的空間關系研究主要集中在面料、放松量與著裝間隙量的關聯。徐繼紅等[3-4]從服裝合體性角度研究了服裝松量、面料性能與服裝廓體松量的配伍關系；張愛萍等[5]采用三維掃描儀采集間隙量數據，建立了特定角度處的距離松量與平均距離松量的相關關系和回歸方程；Agne等[6]和于淼等[7]通過研究織物力學性能與服裝空間形態、體積的關系，改進了三維虛擬試衣軟件的適體性，提出織物性能影響衣下空間體積的回歸方程。而在現有應用的服裝CAD軟件中，人體著裝模型主要根據織物物理仿真的彈簧質點模型和曲面碰撞檢測方法進行構建，其方法對于寬松服裝而言建模效果較差，主要原因是缺乏差異體型和不同面料下的間隙量數據。

服裝依附于體表進而形成千姿百態的造型，從空間構成要素分析，人體形態特征對間隙量構造與分布起著基礎且關鍵的作用。上述學者主要是以尺寸松量和面料物理性能對衣下間隙量分布影響為研究對象，而對于人體形態對著裝衣下間隙量分布的影響研究鮮有見到。

本論文以人體的體表形態凸角對腰部截面間隙量的影響為研究對象，采用補正人臺的方法構造遞進的體表形態凸角，利用三維掃描儀采集凈體與著裝2種狀態下的點云數據，通過Geomagic軟件重建著裝模型后，計算體表點法線方向的距離來確定著裝腰部間隙量值，分析不同松量下體表形態的胸突角和背入角與間隙量分布的相關性，并建立腰截面間隙量與胸突角、背入角及腰圍松量之間的回歸公式。研究結論對不同體型其號型服裝的合體程度，基于局部特征的服裝個性化樣板生成，以及虛擬試衣軟件中間隙量的設置具有參考意義。

1 實驗部分

1.1 體表形態凸角

女子體型分類中人體的軀干表面共形成7個角度：肩斜角、體側角、胸突角、背入角、背側角、臀突角、腹突角[8]。由于本文研究胸腰形態對腰部間隙量的影響，因此選取胸突角和背入角這2個能體現胸腰形態特征的體表角度作為研究對象，如圖1所示。

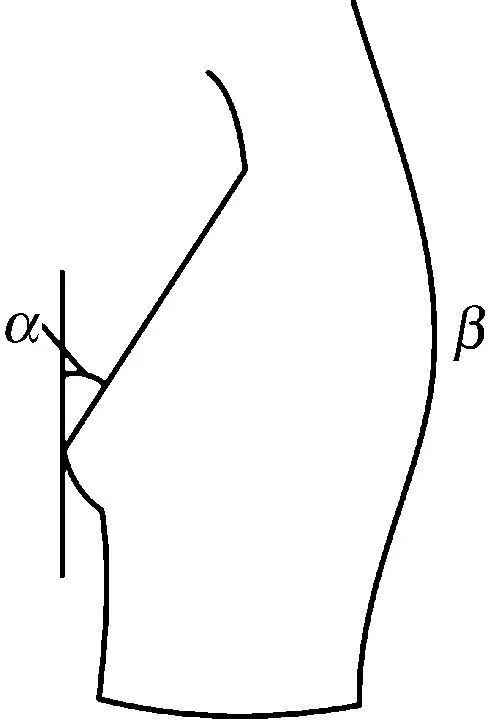
注：α為胸突角； β為 背入角。

1.2 人臺改造

靜止狀態下同一形態人臺和真人的著裝間隙量分布規律基本無差異，采用人臺作為著裝載體能夠固定著裝姿勢。為避免呼吸、站姿等因素對體表角度和間隙量的影響，本文采用在人臺上穿著不同厚度胸衣對人臺進行補正，并采集補正后人臺的著裝間隙量值。所用人臺為國家標準人臺(如圖2所示)高度為160 cm，胸圍為84 cm，腰圍為66 cm，臀圍為90 cm。在人臺初始的胸突角和背入角基礎上，構造了穿著6種不同厚度胸墊人臺的胸突角(如圖3所示)。通過測量角度，將其編號為X1～X7并作為胸突角的參數規格。同理，在原有背入角的基礎上，以2°為1個檔差制作3個具有差異的背入角人臺并將其編號為Y1～Y3(分別為13.96°，15.96°，17.96°)。具體樣本規格參數見表1。

圖2 實驗人臺Fig.2 Experiment mannequin

圖3 胸突角測量

表1 胸突角規格參數表

1.3 樣衣制作

本文選取淺色的棉布作為實驗用樣衣材料，設計并制作8件不同放松量的無領無袖樣衣，編號為1#～8#。在貼體(胸圍放松量0～4 cm)、合體(胸圍放松量6～12 cm)和寬松(胸圍放松量16～24 cm)的3類服裝規格中，分別以胸圍1、2和3 cm為檔差制作1件貼體、4件合體和3件寬松規格的樣衣。所有樣衣的臀圍與胸圍相同，貼體和合體樣衣腰圍比胸圍小16 cm,寬松樣衣腰圍比胸圍14 cm[9]。具體樣衣規格見表2。

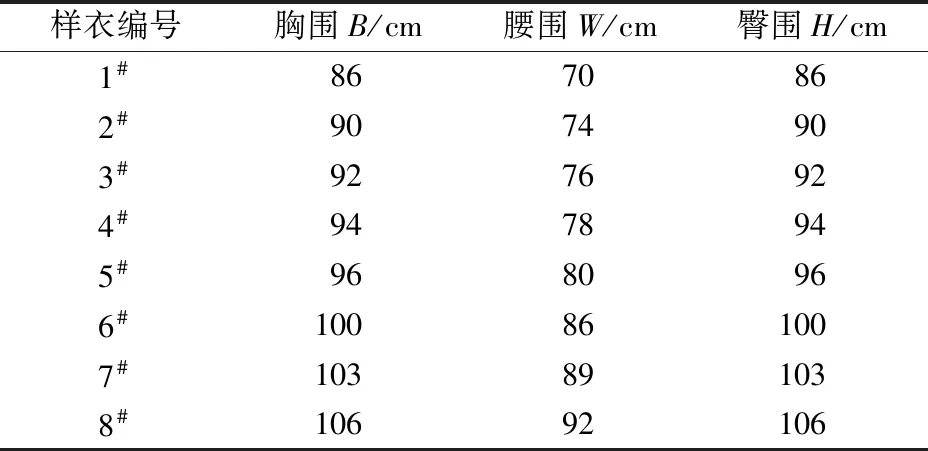
表2 樣衣規格表

1.4 實驗過程

實驗設備采用[TC]2三維人體掃描儀。首先，確定人臺位置與姿勢，得到人臺凈體的三維數據，保持人臺位置和姿勢不變，分別穿著1#～8#樣衣進行掃描，得到1#～8#樣衣穿著狀態下的三維點云數據。然后，對穿著胸墊的補正人臺進行掃描，得到補正人臺數據，保持補正人臺位置和姿勢不變，依次套入1#～8#樣衣進行掃描并得到三維點云數據。以同樣的方法，獲得背入角補正后的凈體人臺和穿著8件樣衣的三維點云數據。為避免實驗操作的人為誤差，每件樣衣在每個檔差規格下掃描3次，無異常情況下取均值數據作為實驗結果。

1.5 腰截面間隙量獲取

1.5.1 腰截面坐標數據讀取

將三維人體掃描儀得到的點云數據導入到Geomajic 軟件，刪除人體軀干以外的其他的部位，如圖4所示。在凈體人臺模型中導入著裝模型，將 2個模型以位置坐標為基準進行注冊對齊，具體見圖5。在Geomajic軟件中采用構建平面[10]的方式選取研究所需的腰圍截面，然后采用等距離采樣法采集腰圍截面上60個坐標點的坐標，采用多項式分段擬合人體和服裝的腰圍截面曲線。

圖4 著裝前后人臺衣身

1.5.2 腰截面間隙量數學模型

著裝間隙量狹義上是指同一水平面上人體到服裝的最短距離[11]，本文采用人體腰截面表面點到服裝的法線距離來定義腰截面處著裝間隙量。

設人體腰截面上點A(a1,b1)處曲線方程為f(x),則該點的法線方程為

(1)

該法線與服裝上的2個相鄰點D1、D2的連線交點為B1，與服裝的交點為B，如圖5所示。

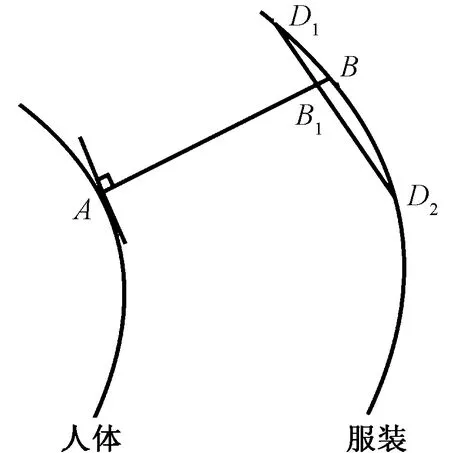
圖5 人體法線與服裝交點

將法線方程(1)改寫為

A1x+B1y+C1=0

(2)

直線D1D2的方程為

A2x+B2y+C2=0

(3)

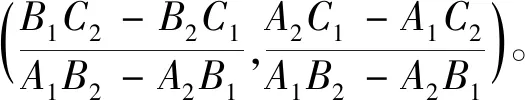
設通過點D1、D2的服裝曲線函數為

(4)

將法線方程(1)改寫為

N(x)=ex+g

(5)

則法線與服裝的交點B為q(x)=g(x)-N(x)的一個零點。

采用牛頓迭代公式，利用B1點作為初始值對q(x)采用式(5)進行迭代：

(6)

式中ai是點B1的橫坐標，一般通過牛頓迭代公式迭代幾次就可以得到B點的橫坐標a2,將a2代入式(5)中即可求出B點的縱坐標b2。

則腰截面處人體法線到服裝的距離(見圖6)為

(7)

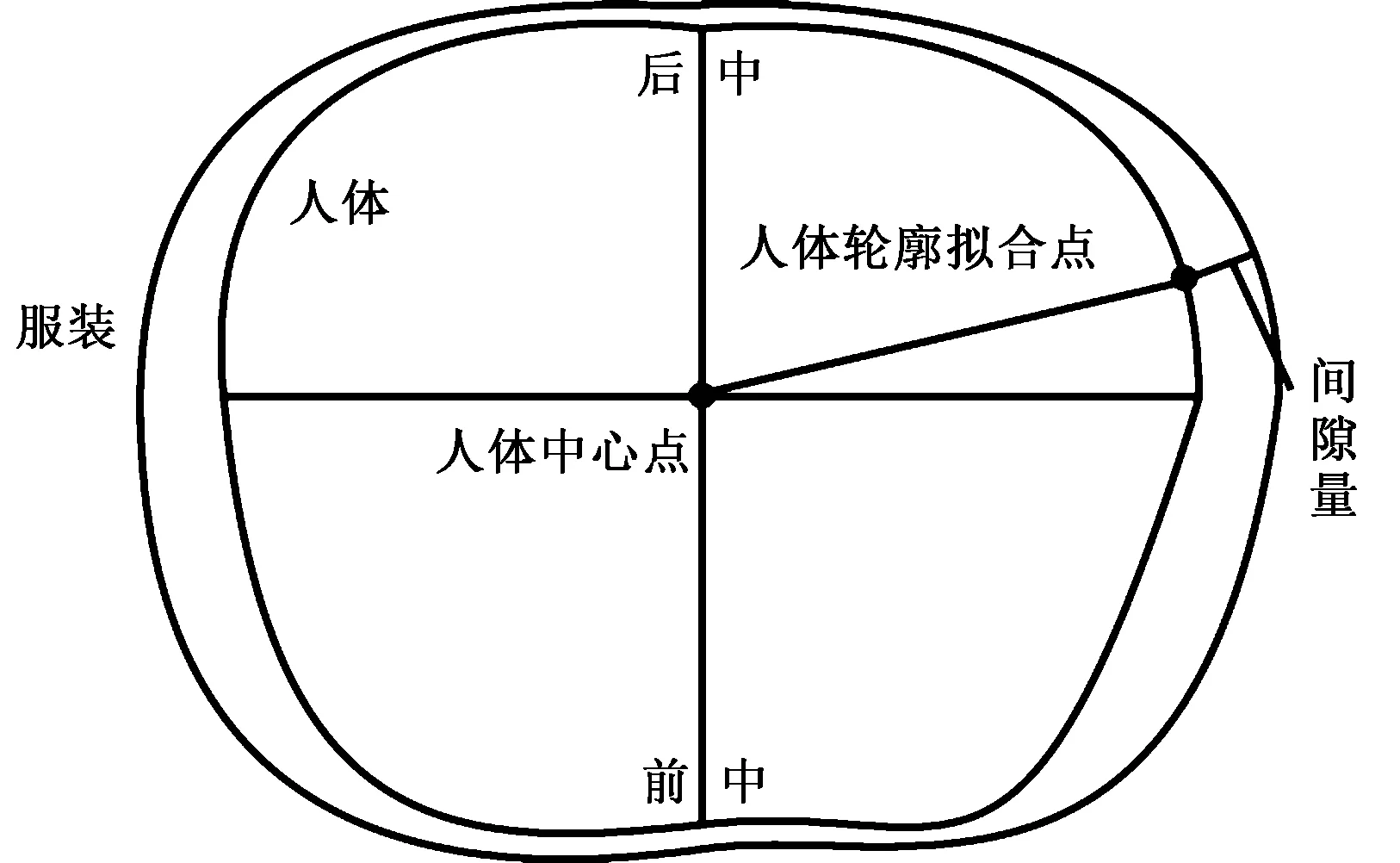
圖6 腰截面間隙量示意圖

2 間隙量與體表形態凸角的關系

為更清晰地表示體表形態凸角與間隙量分布的關系，以人體截面中心為坐標原點，每隔30°角作1條射線對腰圍截面進行區域分割，如圖7所示，計算各角度區域的間隙量的分布特征。

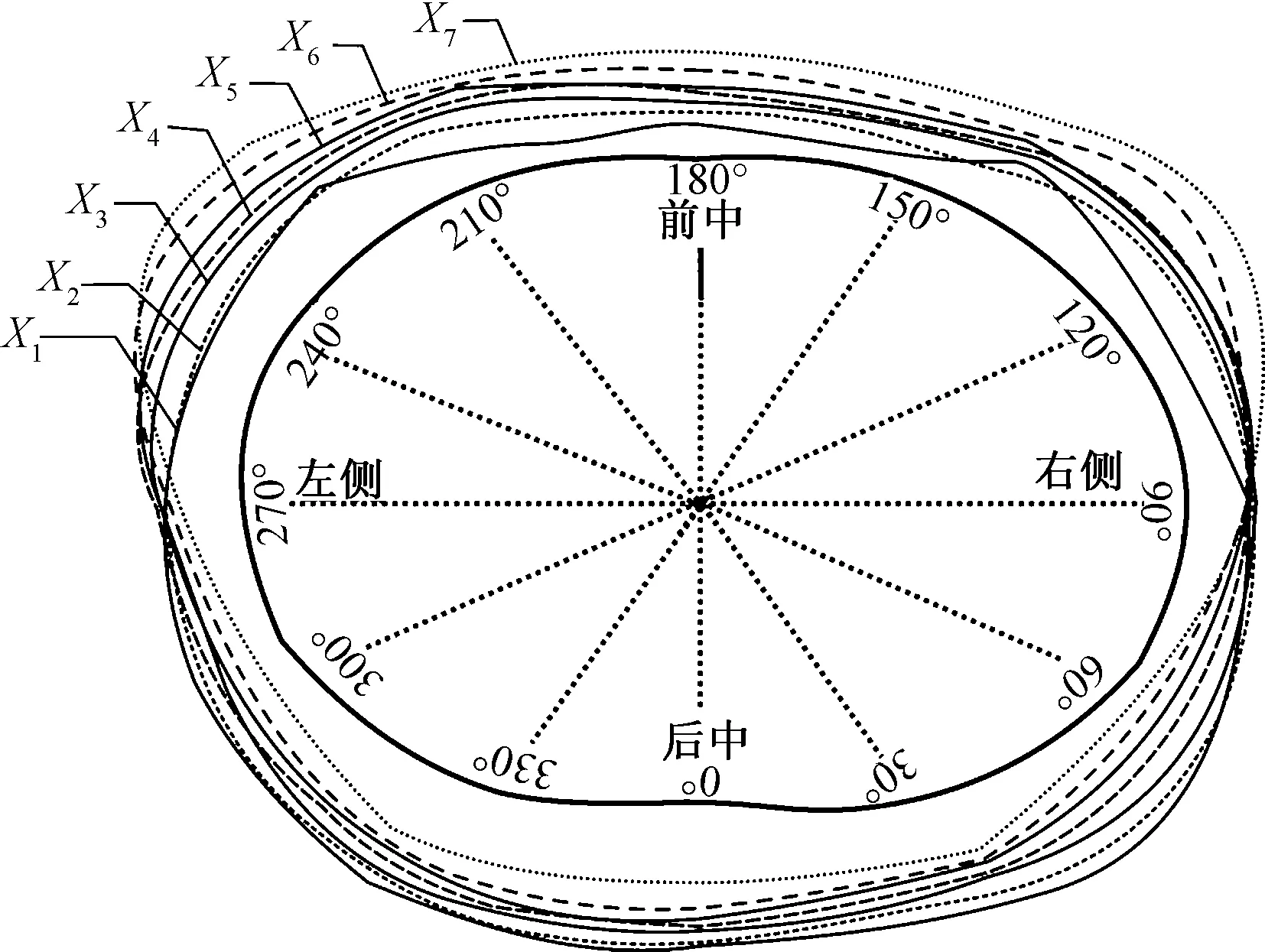
圖7 不同胸突角腰圍截面圖

2.1 腰截面間隙量與胸突角的關聯分析

圖8示出不同背入角的腰圍截面圖。可以看出腰圍截面間隙量的分布基本是以縱坐標為軸對稱變化。為便于分析和表述，本文選取右邊0°～180°區域為對象，研究腰截面間隙量的分布規律。

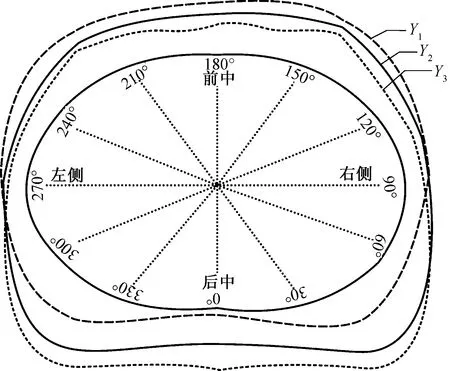
圖8 不同背入角的腰圍截面圖

2.1.1 胸突角單因素分析

圖9示出不同胸突角的腰圍面間隙量分布，發現腰部間隙量整體呈現非均勻分布。胸突角為X1時，間隙量在人體的側面60°～120°區域分布較大，且在60°～90°區域的分布大于90°～120°區域，即人體后腰的間隙量大于前腰的間隙量。這是因為這些區域位于腰圍的側面部分，由于后面有肩胛骨的支撐，前面有BP點的支撐，使得該區域相對較平坦，間隙量集中在該部分；隨著胸突角度的增加，間隙量的分布從0°～60°區域逐漸轉移至60°～180°區域，其中大部分轉移至側面60°～120°區域；由于手臂的因素，在90°區域間隙量并無明顯變化，而在120°區域，間隙量大小與胸突角呈顯著性正相關，相關系數為0.941。

2.1.2 放松量與胸突角聯合分析

在人體側面即60°～120°區域，間隙量數值與腰圍放松量檔差呈現正相關變化。而在0°～60°區域與120°～180°區域，放松量較小的樣衣即1#～4#，后腰的間隙量小于前腰，放松量較大的樣衣即5#～8#，后腰間隙量大于前腰。

胸突角度的變化對不同放松量下的服裝腰截面間隙量分布有著顯著的影響。對于2#～5#樣衣，隨著胸突角的增加，間隙量從30°～60°區域向60°～180°區域轉移，且這種趨勢在樣衣5#中最為明顯，其中120°區域間隙量與胸突角呈高度正相關變化,相關系數為0.941。這是由于人體左右兩側BP點的支撐使得前中部位形成較為穩定的空間，當胸突角度從X1～X7增加時，前中部分即120°～180°區域的間隙量值逐漸變大；對于1#、6#～8#樣衣，胸突角與間隙量之間呈弱相關變化，雖然隨著胸突角的增加，間隙量的分布也從0°～60°區域向60°～180°區域轉移，但其變化量并不明顯。這是因為貼體型服裝在腰部一般緊貼人體，胸突角的變化并不會對間隙量分布產生大的影響，而松量過大的服裝，BP點對服裝的支撐作用小于重力對服裝的作用，改變胸突角的大小無法對間隙量分布產生影響。

2.2 腰截面間隙量與背入角的關聯分析

2.2.1 背入角單因素分析

隨著背入角的增大，0°～90°區域的間隙量增大，其中0°～60°區域間隙量與背入角呈高度正相關變化，相關系數均高于0.9。在0°～30°區域相關顯著性均為0.001；90°～180°區域的間隙量變小，其中120°～180°區域間隙量與背入角呈中度負相關變化，相關系數都在-0.8以上；由于手臂的原因，90°區域間隙量與背入角變化無關聯。

2.2.2 放松量與背入角聯合分析

背入角大小對不同松量服裝有著差異化的影響。對于1#樣衣，背入角的變化對間隙量分布的影響較小，在0°～30°區域間隙量與背入角呈低度相關變化，在60°～180°區域間隙量與背入角無相關關系，這是因為貼體型服裝腰部間隙量的大小受肩胛支撐點的影響很小；對于2#～8#樣衣，隨著背入角的增大，間隙量的分布發生變化，在0°～60°區域的顯著性均小于0.01其中后中部位0°～30°區域的相關顯著性均達到了0.001，相關系數在0.9以上。這可以解釋為人體左右兩側肩胛點對具有一定松量的服裝有支撐作用，背入角越大肩胛骨就越突出，從而導致后中部位間隙量發生明顯變化；120°～180°區域的相關顯著性均小于0.05，進一步說明背入角對具有一定松量服裝的腰部間隙量分布有顯著影響。

3 回歸分析

從上述的2.1、2.2節分析得知，在2#～5#樣衣中腰截面間隙量與胸突角、背入角及腰圍放松量呈現了高相關性，因此，本文針對0°、30°、60°、120°、150°和180°區域的腰截面間隙量，以胸突角、背入角及腰圍松量為變量，進行多元線性回歸分析[12]。回歸方程如表3所示，定義y為特定角度處的間隙量，x為腰圍松量，α為胸突角，β為背入角。

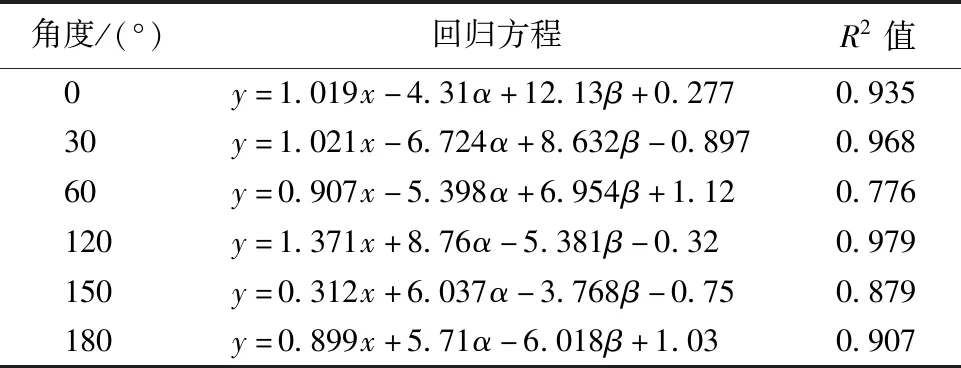
表3 不同角度處間隙量的回歸方程

在各區域的回歸分析中，30°區域和120°區域的間隙量與胸突角、背入角及腰圍松量的相關性系數最高，回歸方程的擬合優度也最好，回歸方程的R2值都達到0.95以上。60°區域和150°區域的相關系數稍低，回歸方程的擬合優度稍差，回歸方程的R2值分別為0.776和0.879。

4 結 論

本文將體表形態凸角作為研究腰部著裝間隙量分布規律對象，通過[TC]2三維掃描儀的測量實驗，獲得系列檔差胸突角、背入角的補正人臺及其穿著不同松量樣衣的點云數據，計算得到腰截面各區域間隙量的數值，得到體表凸角與腰部間隙量分布的關聯。

實驗結果顯示：1#樣衣腰截面間隙量不受胸突角和背入角的影響，2#～5#樣衣同時受胸突角和背入角的影響，6#～8#樣衣受背入角影響，不受胸突角影響；其中胸突角對腰截面120°區域影響最大，背入角對0°～30°區域影響最大；胸突角和背入角都對側縫區域的間隙量無影響；30°區域和120°區域間隙量與胸突角、背入角及腰圍松量回歸方程擬合優度較好，回歸方程的R2值為0.968和0.979。這些結論對于下一步研究如何將間隙量分布轉化為樣板修改規則，以及提高虛擬試衣的仿真程度有著很好的參考和意義。