對一道中考適應性填空題解法的探究

浙江省紹興市柯橋區平水鎮中學 (郵編：312050)

數學家哈爾莫斯說過“問題是數學的心臟”．對問題進行研究是教師的一項基本功．通過研究，挖掘其隱含的問題的本質，獲得豐富的教學資源．這樣做，不僅能提高教師自身的專業素養，還有利于開闊學生的思路，培養學生的創新能力．現以2019年5月柯橋區中考適應性九年級數學的一道填空題為例，對其解法方法進行探究，愿與大家共同分享．

1 試題呈現

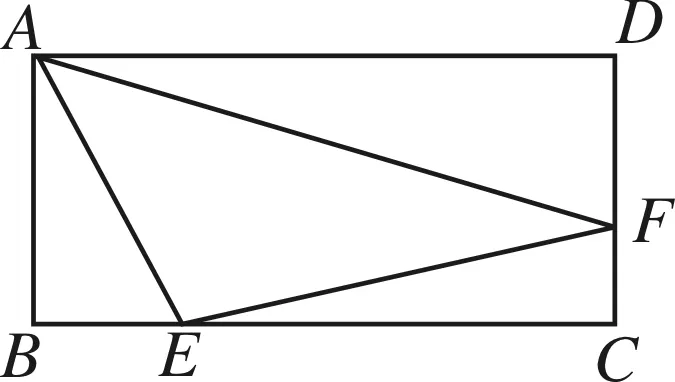
圖1

本題源于2018年山東省濱州市的一道中考填空題，此題雖內容平實、條件簡潔，但內涵深刻，學生深感望“題”興嘆．據此，筆者細研此題，發現此題切入點多，方法多樣，給學生留有較大的思維空間，可以呈現出不同的解題方法．現把此題的幾種常規解題思路整理成文，以期待同行的指正．

2 思路分析

思路1 注意到∠EAF=45°，構造“一線三等角”全等模型

圖2

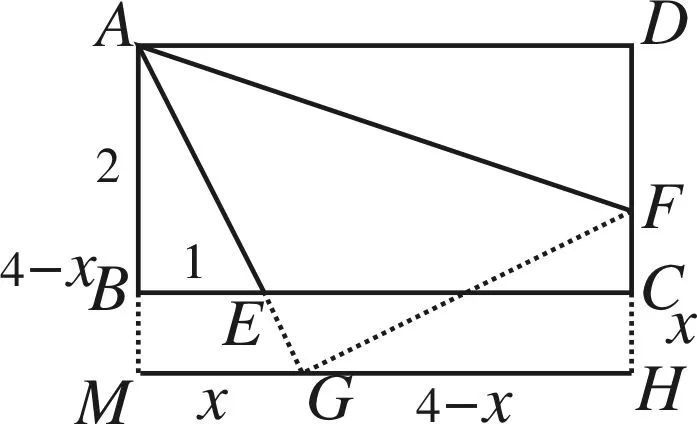
圖3

圖4

圖5

評注抓住核心條件“45°”這個角，從多角度構造“一線三等角”模型是形成上述思路的關鍵．解法1運用“全等+平行線分線段成比例”，解法2、3、4運用“全等+相似三角形”，這些都是解決問題的常用方法，應引起足夠的重視．

思路2 注意到∠EAF=45°，構造正方形中的“半角模型”

圖6

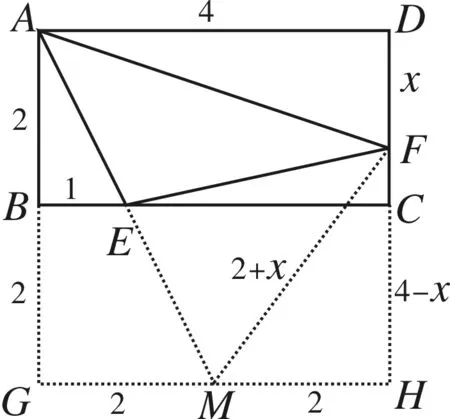
圖7

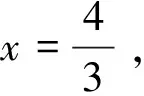
評注抓住核心條件“45°”這個角，由平時積累的解題經驗，結合該矩形鄰邊的特定的關系——2倍長，自然聯想到將長方形中的45°角轉化為正方形中的“半角模型”，借助此模型的相關結論解決問題．由此可見，若眼中有“形”，手中有“數”，心中建“模”，則解法自然來．

思路3 注意到∠EAF=45°，構造“一線三等角”相似模型

圖8

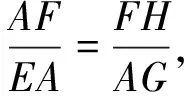
圖9

評注抓住核心條件“45°”這個角，構造出“一線三等角”的相似三角形模型，不過這個基本圖形需要平時深度研究，考生才能在緊張的考場上實現有效的遷移．此法也是十分常見的一種重要構造方法，一旦悟透，解決問題顯得簡潔、快捷．當然，此題也可分別延長DA、AD至點M、N，使得∠ANF=∠EMA=∠EAF=45°，用類似方法解決問題，具體過程留給有興趣的讀者思考．

思路4 運用割、湊，構造相似三角形

圖10

圖11

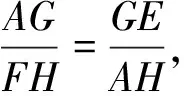
評注抓住核心條件“45°”這個角，構造出“一線三等角”的相似三角形模型．解法9側重于割“45°”這個角構造相似三角形，解法10側重于有“45°”這個角，再湊出兩個45°角而得到相似三角形．當然這需要認真觀察，化“無形”為“有形”，樹立起“有模型找模型，無模型造模型”的解題意識，做到會善于變通、善于轉化．

思路5 構造“A”型和 “8”字型的相似三角形

圖12

評注抓住核心條件“45°”這個角，通過延長AF構造出等腰直角三角形，然后借助“8”字型(△ABE∽△GHE)和“A”型(△ABG∽△FCG)的相似三角形而獲解．可以看出，通過“45°”這個角的中介作用，揭示了命題中條件與隱含條件、結論的內在聯系，為尋求解題途徑指明了方向．

思路6 用面積關系建立方程

圖13

評注面積法在初中數學各模塊的知識中都有所涉及，此題正是注意到圖形的特殊性，利用面積的兩種表示方法建立方程，使一道難題變得清晰、透明，令人拍案叫絕．有時面積法還可以解決網格中的銳角三角函數問題、求線段的長等問題．由此可見，面積法也是一種解決問題的通性、通法，應當予以重視．

思路7 運用旋轉，構造共點雙垂直

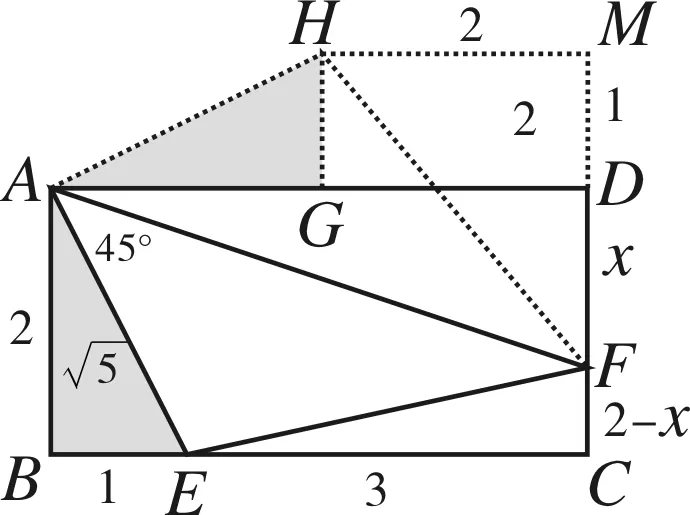
圖14

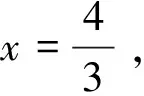
評注當題目中出現45°或90°特殊角時，聯想到“共點雙垂直”模型，由此通過旋轉可得等腰三角形，從而得到△EAF≌△HAF，再借助勾股定理建立方程，求解也就順理成章了．由此可見，采用“旋轉”策略，是通過對題目的深入分析，或聯想，或轉化，挖掘知識模塊內蘊的思想方法，是一種經驗的“噴薄”．讓人不禁感嘆，幾何構造之神奇，“旋一旋”出精彩．

思路8 運用數形結合，建立直角坐標系

圖15

評注解答此題的關鍵是采用數形結合的思想．若考生對題目的特殊性(如90°角)進行多觀察、多思量，就能迸發出建立坐標系的解題思路．一旦找到了解題的切口，再采用旋轉，結合“中點坐標公式”求出AF的解析式，用函數解決計算問題便會水到渠成，就能取得令人驚喜的效果．

思路9 運用平時積累的公式，構造基本圖形求解

圖16

這個結論，其實可借助圖16的網格進行直觀證明，此處不再贅述．基于此，我們可得到下列思路：

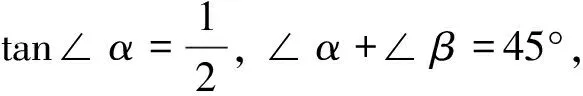
評注本解法是通過一個常見結論的中介作用，揭示了命題中條件與隱含條件、結論的內在聯系，為尋求解題途徑指明了方向，使問題的解法簡單流暢、別具一格．由此可見，一些優秀學生通過自己的自學、吸收、內化，積累一些先進的“武器”，為自己擅長的方式構思或尋求解決問題的方法貯存能量，是一種經驗的“噴薄”，做到該出手時就出手．

3 解法實踐

親愛的讀者，你看了以上的幾種解法，是不是產生了一種躍躍欲試的沖動，那你就動起筆來，思考、挑戰一下兩道變式題吧．

圖17

變式1 如圖17，四邊形ABCD中，AD∥BC，∠BCD=90°，AB=BC+AD，∠DAC=45°，E為CD上一點，且∠BAE=45°，若CD=4，則△ABE的面積為( )

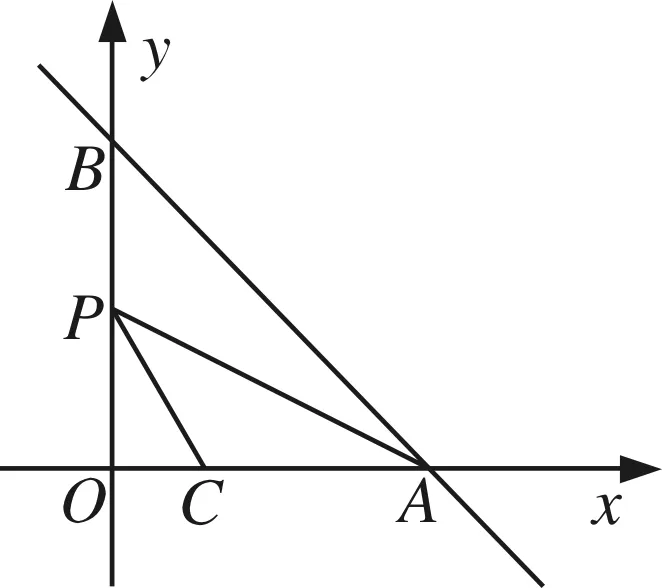
圖18

變式2 如圖18，在平面直角坐標系xOy中，直線y=-x+m分別交x軸，y軸于A，B兩點，已知點C(2，0)．設點P為線段OB的中點，連結PA、PC，若∠CPA=∠ABO，則m的值是．

聰明的讀者，上面的兩道變式題，你能運用哪些方法求解？一題多解，比較解法的優劣；多解一題，領略解法的真諦；多解歸一，感悟數學的魅力．這就要我們在平時的教學中，在總結經驗、掌握通式和通法的基礎上，要多引導學生結合題目的特點一題多解，一題多變，一圖多思，拓寬思路，幫助學生在變式訓練中，發展思維的靈活性和發散性．“解一題，會一類，通一片”，讓學生由此及彼，并感悟出同類問題的深層結構，使得學生下次再碰到類似問題時能快速找到切入點，順利貫通思路，提升解題能力的同時，發展數學洞察力，訓練思維的深度，讓一題多解成就精彩，讓課堂高效起來，讓學生在考場中能有一種經驗的“噴薄” ．