初中數學深度學習的實踐研究

安徽省合肥市教育局教科院 (郵編：230031)

1 深度學習的提出

深度學習的概念源于對人工神經網絡的研究，是指一種主動的、批判性的、建構的和面向問題解決的學習方式，也是實現有意義學習的有效方式.深度學習在教育上的意義是指在教師的引領下，學生圍繞具有挑戰性的學習主題，全身心積極參與、體驗成功、獲得發展的有意義的學習過程.判斷深度學習是否發生的五個標準為：第一，聯想與結構：經驗與知識的相互轉化；第二，活動與體驗：學生的學習機制；第三，本質與變式：對學習對象進行深度加工；第四，遷移與應用：在教學活動中模擬社會實踐；第五，價值與評價：“人”的成長的隱形因素.深度學習發生的條件為：第一,學生思考和操作的學習對象，必是經過教師精心設計，具有教學意圖的結構化的教學材料；第二，教學過程必須有預先設計的方案，要在有限的時空下，有計劃、有序地實現豐富而復雜的教學目的；第三，要有平等、寬松、合作、安全的互動氛圍[1].

2 深度學習的實踐

何謂深度，從工作、認識的角度認為是觸及事物本質的程度[2].

深度學習體現在深度二字上.數學教學若能引導學生用內心創造和體驗的方法來學習數學;鼓勵學生尋求解法，而不是記住步驟；探索模式，而不是模仿題型；形成猜想，而不是僅僅做練習題；幫助和鼓勵學生按自己的想法和語言重建所學的東西；鼓勵學生用學到的知識去修正和改造原有的觀念和想法[3].首先我們在教學實踐中采用任務具體化、推理分步化、應用具體化，使得學生的學習積極參與，獲得成功的體驗[4].其次又圍繞數學教學促進初中生深度學習進行實踐研究.

2.1 概念深剖

數學中的概念是數學的基石.數學大廈是由數學中的概念、定義、定理、公理建立的.數學中的概念是前人日積月累形成的，是前人智慧的結晶.數學概念具有抽象性、嚴謹性，學生在理解上有一定困難.深度學習是有意義學習，應在概念同化的基礎上，達到概念的順應.

案例1 如在上海科技出版社出版的新時代數學編寫組編著的教育部審定(2012)義務教育教科書數學七年級下冊第88-89頁的分式及其基本性質第1課時的教學過程中是這樣設計的：

問題1 (1)一塊長方形木板的面積為10m2,寬為3m，則長為______m；

(2)一塊長方形木板的面積為10m2,寬為am，則長為______m；

(3)一個長方形的面積為Sm2，如果它的長為am，那么它的寬為______m.

問題2 (1)有兩塊稻田，第一塊是4公頃，每公頃收水稻10500kg；第二塊是3公頃，每公頃收水稻9000kg，這兩塊稻田平均每公頃收水稻______kg.

(2)如果第一塊是m公頃，每公頃收水稻akg；第二塊那是n公頃 ，每公頃收水稻bkg，則這兩塊稻田平均每公頃收水稻______kg.

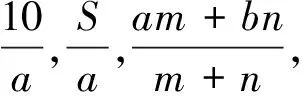
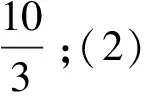
類比分數的除法算式，引出分式的概念.

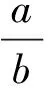
下列式子中，哪些是分式？哪些是整式？

在下列所給的整式中選兩個，你能組合出幾個不同的分式？請都寫出來.

x-2，4，2x-3，x+4.

此環節學生共寫出：

2.2 探索領悟

探索的釋義是多方尋求答案，解決疑問[5].

2011年版義務教育數學課程標準的課程理念要求：課程內容的選擇要有利于學生體驗與理解、思考與探索；學生學習除接受學習外，動手實踐、自主探索與合作交流同樣是學習數學的重要方式.教師教學要引導學生獨立思考、主動探索、合作交流，使學生理解和掌握基本的數學知識與技能、數學思想和方法，獲得基本的數學活動經驗.要有效地改進教與學的方式，使學生樂意并有可能投入到現實的、探索性的數學活動中去.這說明數學中的探索活動對學生的數學理解、領悟有舉足輕重的價值.如

案例2 定理n邊形的內角和等于(n-2)·180°(n為不小于3的整數).

探索1 由三角形出發，到四邊形時從一個頂點出發可以分割成(n-2)個三角形，利用三角形內角和為已知，把未知轉化為已知.如圖1.

圖1

探索2 由四邊形的內部任取一點出發與各頂點連接可以得到四個三角形，內角和為4×180°，減去一個360°，所以四邊形的內角和為(4-2)·180°，類推，過n邊形的內部一點與各頂點連接所得到的n個三角形的內角和為(n-2)·180°.

探索3 由四邊形的某一邊上任取一點出發與不相鄰的頂點連接可以得到三個三角形，內角和為3×180°，減去一個180°，所以四邊形的內角和為2·180°=(4-2)·180°，類推，過n邊形的內部一點與不相鄰頂點連接所得到的n-2個三角形的內角和為(n-2)·180°.

探索4 由四邊形的外部任取一點出發與各頂點連接可以得到三個三角形，內角和為3×180°，減去一個由該點和所對邊組成的三角形的內角和為180°，所以四邊形的內角和為2×360°，所以四邊形的內角和為(4-2)·180°，類推，過n邊形的外部一點與各頂點連接所得到的n個三角形的內角和為(n-2)·180°.

從而讓學生在探索中領悟解決疑問的思想是未知轉化為已知.

2.3 思維遞進

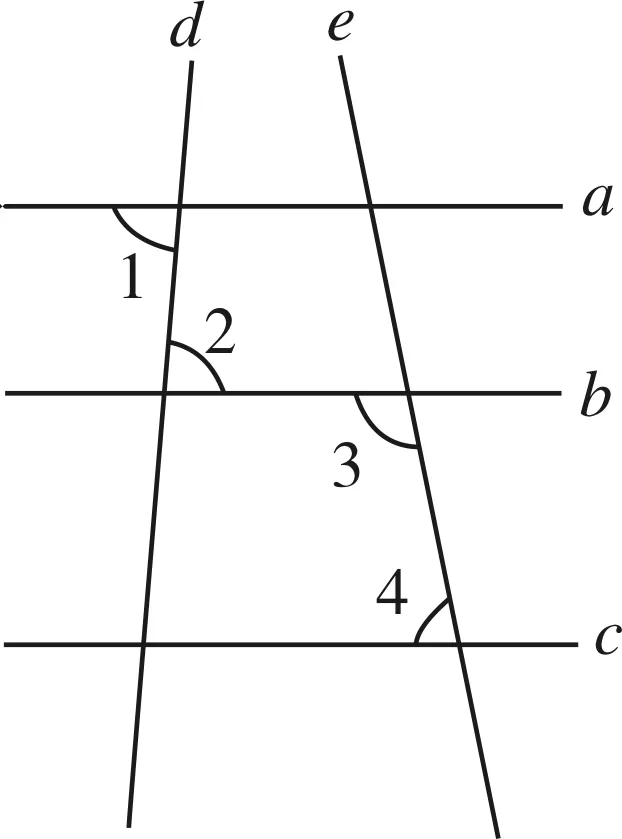
圖2

深度學習是階梯式的學習，教師根據學生的認知水平，設計由淺入深、由表及里的解題過程，能讓學生的數學學習與思維不斷深入.如在平行線判定方法的應用教學時，教師設計如下系列問題：

問題1 如圖2所示,已知直線a、b、c、d、e，且∠1=∠2，∠3+∠4=180°，則a與c平行嗎?為什么?

利用平行線判定方法可得.

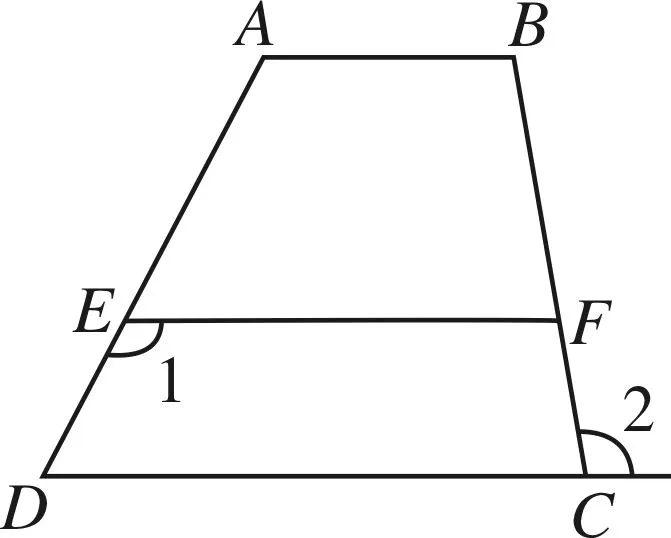
圖3

問題2 如圖3，如果∠1=∠A，∠2=∠B，那么直線EF∥DC嗎？為什么？

利用平行線判定方法和平行的傳遞性可得.

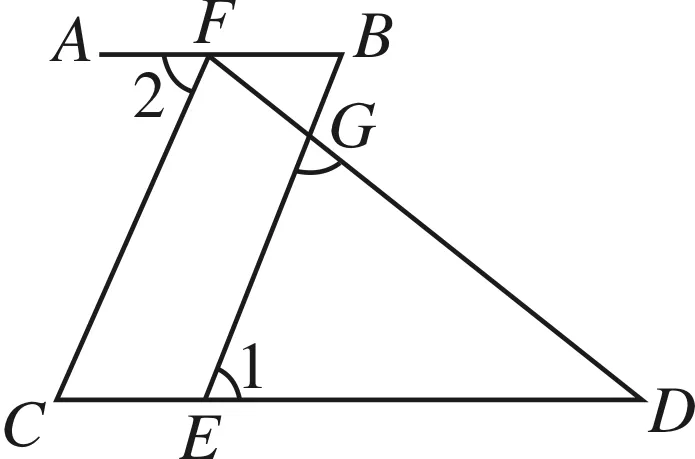
圖4

問題3 如圖4，∠C=∠1，∠2與∠D互余，BE⊥DF，垂足為G．求證：AB∥CD．

利用平行線判定方法、余角性質、三角形內角和定理可得.

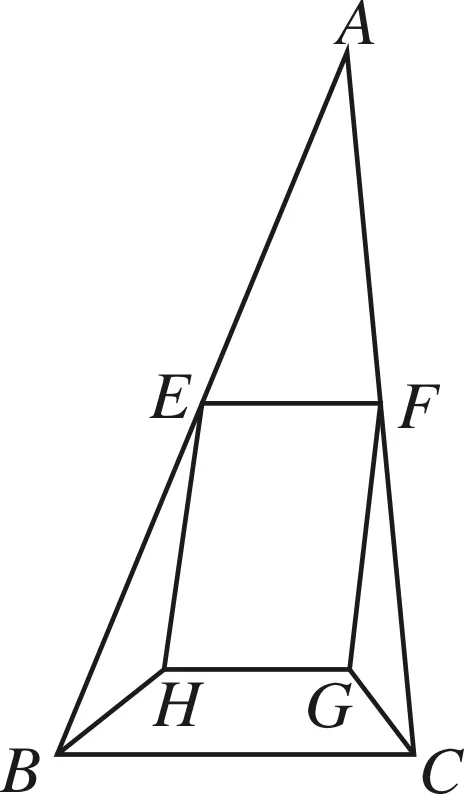
圖5

問題4 如圖5，已知∠BEH+∠AEF=90°，EH⊥HG，∠ABH+∠HBC=∠AEF，求證：HG∥BC.

利用平行線判定方法和垂直定義可得.

該系列問題由淺入深、由表及里，思維不斷深入.

2.4 運算熟練

深度學習是主動式的學習，教師要不失時機地給學生提供主動學習的機會.而設計不同形式的運算，能激發學生主動學習的心向.如在滬科版初中數學九年級上冊第119頁的任意一個銳角的正(余)弦值，等于它的余角的余(正)弦值的教學中，教者采用頭腦風暴的形式完成如下填空：

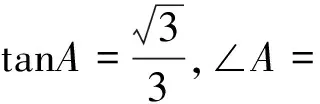
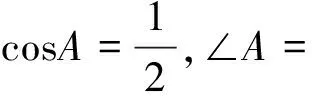
sin45°=.

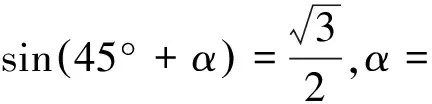
sin30°-cos60°=.

sin45°-cos45°=.

這幾個式子的運算，不僅有對30°,45°,60°特殊三角函數值的回憶，也有逆向思維的訓練.

接著思考：30°,45°,60°這三個角的正(余)弦值和它們余角的余(正)弦值有什么關系？從特殊到一般 歸納出“任意一個銳角的正(余)弦值，等于它的余角的余(正)弦值.”即是sinA=cosB=cos(90°-∠A)，cosA=sinB=sin(90°-∠A).

給出結論的直接應用：已知sin22°=0.3746,cos22°=0.9272，求68°的正弦、余弦的值.

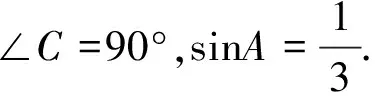
(1)求cosB的值；

(2)求sinB、tanB的值.

思考sinα、cosα、tinα之間有何關系？sinα、cosα之間有何關系？

教者在結論基本鞏固的基礎上，安排如下當堂練習：

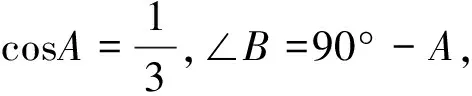
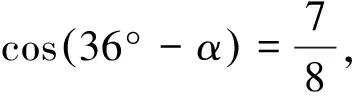
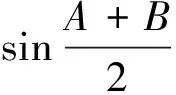
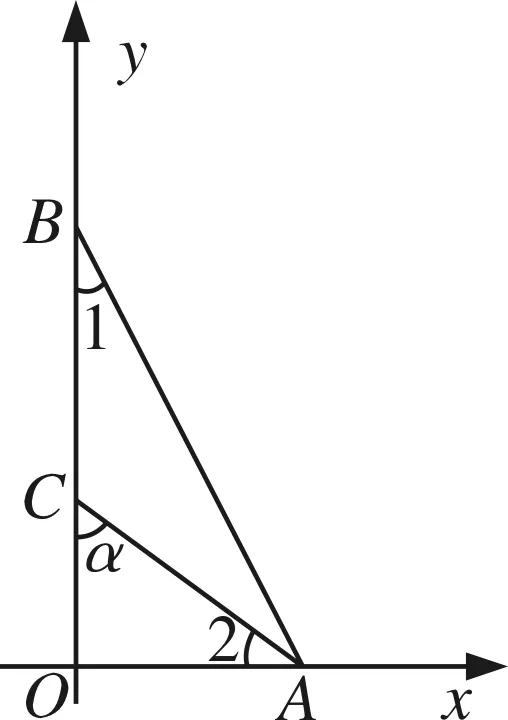
圖6

5.如圖6，已知兩點A(2,0),B(0,4)，且∠1=∠2，則sinα=.

練習1是直接利用結論解決；練習2運用整體思想和結論解決；練習3利用三角形內角和定理和結論解決；練習4利用結論解決.

練習5的解法二因為A(2,0),B(0,4)，

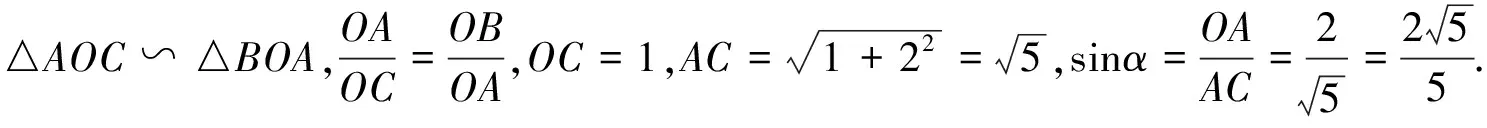
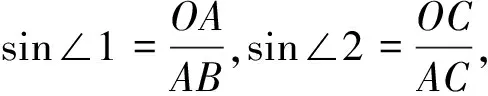
又△AOC為直角三角形，OC2+OA2=AC2，兩式聯立解得

本部分雖然以運算為主，但滲透方程、整體、特殊到一般的思想和發散性思維的培養.

2.5 問題變式

圖7

深度學習是理解性學習，教師要對問題進行深層次加工，引導學生通過深切的體驗與深入的思考，達成對問題的理解.對問題的變式就是深層次的加工，對問題變式的求解過程可以加深對問題的理解.如三角形的復習課安排如下問題：

案例3 已知：如圖7，△ABC中，AB=AC,∠A=90°,BD平分∠ABC,CE⊥BD，垂足為E，求證：BD=2CE.

略證延長CE,BA相交于F，可證△CAF?△BAD，

BD=CF，∠BCF=∠BFC=67.5°，△BCF是等腰三角形，BE⊥CE，E為CF的中點，所以BD=2CE.

變式一已知：如圖7，△ABC中，AB=AC,∠A=90°,D是AC上一點，CE⊥BD，垂足為E，BD=2CE，求證：BD平分∠ABC.

略證延長CE,BA相交于F，∠BDA=∠CDE，∠DCE+∠CDE=90°,∠DCE+∠CFA=90°，可證△CAF?△BAD，BD=CF，

CF=2CE，E是CF的中點，BE⊥CE，BD平分∠ABC.

變式二 已知：如圖7，△ABC中，∠A=90°,D是AC上一點，CE⊥BD，垂足為EBD=2CE，BD平分∠ABC,求證：AB=AC.

略證延長EF=CE與BA相交于F，因為BD平分∠ABC，所以BC=BF，

∠BCF=∠BFC，∠BFC+∠FBE=90°，又∠ADB+∠FBE=90°，∠BFC=∠ADB，∠CDE+∠ECD=90°，∠CDE=∠ADB，∠ECD=∠ABE，可證△CAF?△BAD，可得AB=AC.

變式三已知：如圖7，△ABC中，AB=AC，D是AC上一點，CE⊥BD，垂足為E，BD=2CE，BD平分∠ABC,求證：∠A=90°.

略證延長EF=CE與BA相交于F，因為BD平分∠ABC，所以BC=BF，

∠BCF=∠BFC，∠BFC+∠FBE=90°，∠ACB+∠ECD+∠EBC=90°，

∠EDC=∠ACD+∠EBC，又∠EDC+∠ECD=90°，∠ECD=∠EBC，AB=AC，可證△CAF?△BAD，可得∠FAC=∠BAC,可得∠A=90°.

圖8

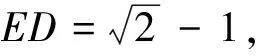
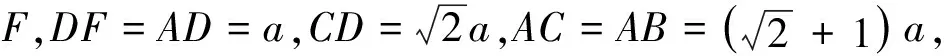
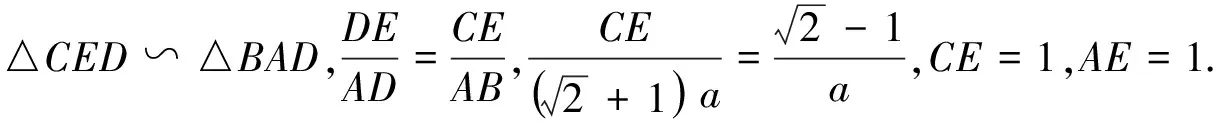
變式五已知：如圖8，△ABC中，AB=AC，BD平分∠ABC交AC于D，CE⊥BD，垂足為E， 且BD=2CE，連接AE，猜想BE,CE,AE之間的關系并證明.

略解延長CE,BA相交于F，由已知可證∠A=90°，設AE=x,CE=y,BD=2y，

將一題演變成多題，而題目實質不變，讓學生解答這樣的題目，能隨時根據變化的情況思考，從中找出它們之間的區別與聯系，以及特殊與一般的關系，達到對問題的加深理解.

3 幾點建議

3.1 處理好深度學習與行為主義，認知主義，人本主義，建構主義[6]的關系

深度學習源于人工神經網絡的研究，按其釋義和在教育上的釋義，似乎涵蓋了上述四種學習的理論，是否可以說深度學習是上述四種學習的上位學習？實質上，行為主義的數學教學強調教師是知識的傳授者，學生是知識的接受者；教學內容要化整為零；教學目標細化.認知主義的數學教學強調教師與學生是教學的雙主體；根據學生信息加工過程來考察教學活動；強調在教學中發展和培養學生的認知和元認知能力；提倡“問題解決”.人本主義的數學教學注重情感教育；構建真實的問題情境，提倡從做中學，鼓勵學生自由探索；提倡課堂的創造活動；合作學習.建構主義的數學教學要求學生通過高級思維活動來學習，學習者要不斷思考和對各種信息進行加工轉換，基于新經驗與舊經驗進行綜合概括去建構知識.總的來說是教師為主導的教向學生為主體的學的轉變.深度學習的數學教學就是要求教師給學生提供主動的、批判性的、建構的和面向問題解決的學習素材，實現有意義學習.

3.2 處理好深度學習與面向全體的關系

初中教育屬于義務教育，小學是就近、劃片、免試升入初中.學生存在數學學習的差距是必然的.在這樣的班級上，課堂教學中如何使學生進行深度學習呢？筆者認為，在創設情境時盡量聯系生活實際，在探索問題時盡量設置臺階，在安排運算時盡量由淺入深，在進行問題變式時盡量面向全體，在進行思維訓練時盡量在最近發展區內.

3.3 處理好深度學習與教師理解的關系

深度學習并不能自然發生，它需要促發條件.其中，先決條件是教師的自覺引導.深度學習中學生思考和操作的學習對象，必是經過教師精心設計、具有教學意圖的結構化的教學材料；教學過程必須有預先設計的方案，要在有限的時空下，有計劃、有序地實現豐富而復雜的教學目的.因此，教學中教師必須理解深度學習發生的標準和條件，深刻理解教材中實施深度學習的素材，設計好進行深度學習的方案，有條不紊地組織學生探索新知識的活動.

總之，教師對教學內容的深度理解、學生認知情況的深度分析是進行深度學習的出發點，恰當且有深度的學習目標是導航，好的引導問題、有吸引力的學習活動是深度學習的核心和關鍵，精準、及時的評估是深度學習的保障.

本文特別致謝合肥市第六十八中學數學組孫自海、韓芬芬、錢雪、楊菊、王春苗老師提供的教學實例.