軸承自旋運動的分析

(天津工業(yè)大學機械工程學院 天津 300387)

一、軸承的運動分析

球軸承中，滾珠的運動形式十分復雜，不僅有繞軸承軸線的公轉(zhuǎn)，同時還有繞自身軸線的自轉(zhuǎn)運動。當接觸角大于零時，即對于角接觸球軸承，滾珠還會產(chǎn)生相對滾道的自旋運動以及由于陀螺力矩導致的陀螺旋轉(zhuǎn)。高速輕載時，軸承中還可能出現(xiàn)公轉(zhuǎn)打滑現(xiàn)象。因此，高速軸承，尤其是高速角接觸球軸承的運動學計算，需要通過建立相應(但復雜)的運動方程求解滾動體的運動。

假設滾珠的中心固定在空間中，軸承的內(nèi)圈以ωi的角速度進行旋轉(zhuǎn)，內(nèi)圈與滾動體產(chǎn)生的接觸橢圓在內(nèi)圈滾道上最多出現(xiàn)兩個純滾動點，把出現(xiàn)純滾動點的半徑記為ri，如圖1所示。

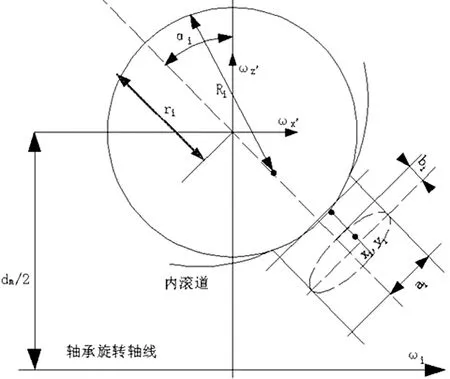
從圖中可以推導出滾珠和內(nèi)滾道在接觸橢圓短軸方向的滑動速度

滾珠和內(nèi)滾道在接觸橢圓長軸方向的滑動速度

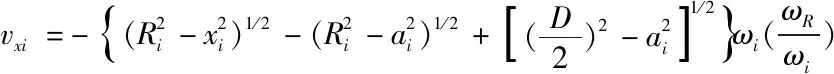
滾珠相對于內(nèi)滾道的滑動速度

同樣對于外滾道與滾珠的接觸可以推導出滾珠和外滾道在接觸橢圓短軸方向的滑動速度

滾珠和外滾道在接觸橢圓長軸方向的滑動速度

cosβsinβ′

滾珠相對于外滾道的滑動速度

若采用外滾道控制理論，即假設滾珠在即假設滾珠在外滾道上發(fā)生純滾動無自旋，可使計算簡化。同時，由于軸承使用中應防止陀螺旋轉(zhuǎn)的發(fā)生，故在忽略陀螺運動情況下，對于外圈固定、內(nèi)圈旋轉(zhuǎn)的軸承，滾珠公轉(zhuǎn)角速度、自轉(zhuǎn)角速度及相對于內(nèi)滾道的自旋角速度的計算公式分別為

本文中218角接觸球軸承為例對軸承運動進行了計算，軸承的具體參數(shù)如表1所示以及運用matlab對上述公式進行求解，求得的結(jié)果如表2所示。

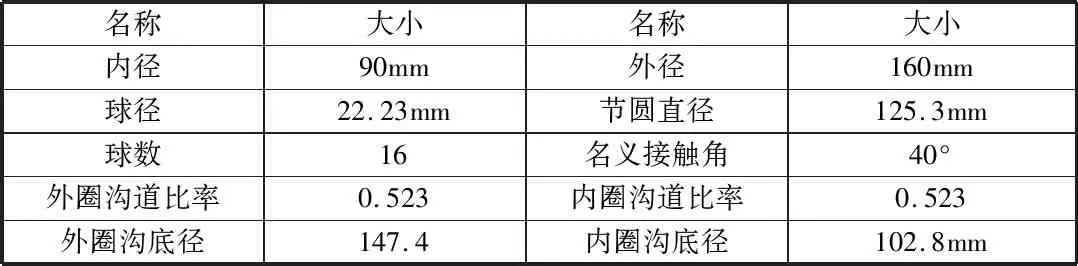
表1 軸承參數(shù)

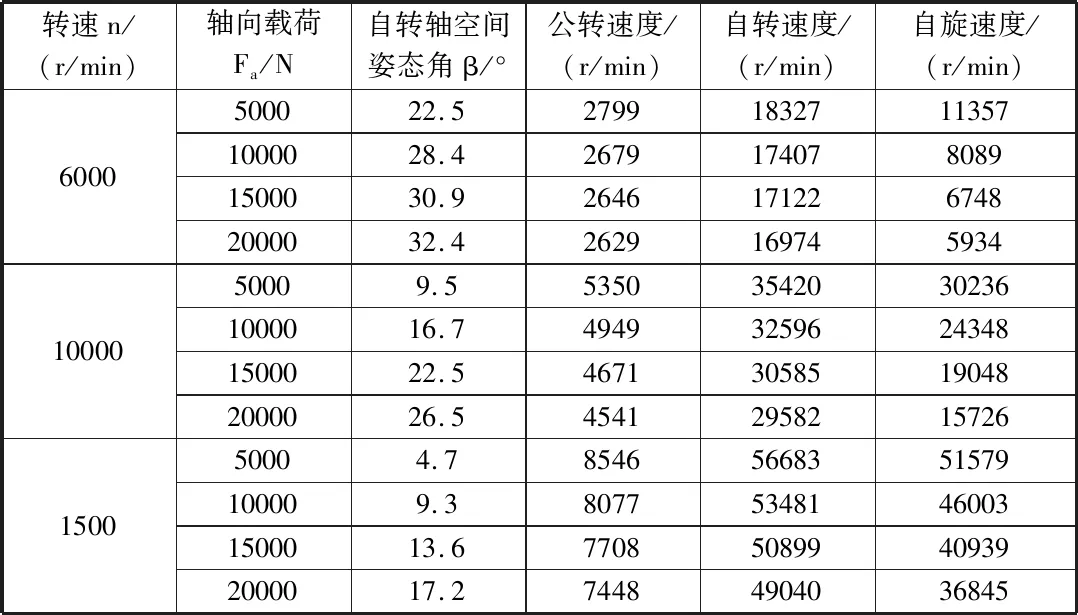
表2 軸承運動學分析結(jié)果

二、結(jié)論

(1)相同載荷時，軸承的自旋速度隨著轉(zhuǎn)速的增加而增加，并且通過數(shù)據(jù)可以得之自旋速度增長的速率在降低。(2)相同轉(zhuǎn)速時，隨著載荷的增加軸承的自旋速度是降低的，這是因為軸向載荷的增加導致滾珠與內(nèi)外圈之間的摩擦增大，因此自旋速度會降低。