高速角接觸球軸承保持架不穩定運動機理分析

張 濤，陳曉陽，顧家銘，趙利鋒

(1.上海大學 機電工程與自動化學院，上海 200072；2.上海天安軸承有限公司，上海 201108；3.上海集優機械股份有限公司軸承研發中心，上海 201108)

作為關鍵支承部件的角接觸球軸承，在精密機床、新能源汽車、航空航天等領域有著十分廣泛的應用。隨著主機工作性能要求的提高，對軸承的轉速、旋轉精度和可靠性提出了更高的要求。保持架的不穩定運動，一方面會使軸承摩擦力矩波動，產生振動和嘯叫聲；另一方面，會導致保持架與球及套圈擋邊的碰撞力增大，從而加劇接觸副的摩擦磨損，當磨損量達到一定值時，會使軸承不能滿足主機工作精度要求而提前失效[1]。保持架的過量磨損和嚴重失穩甚至會導致保持架突然斷裂，致使軸承卡死而引起災難性的后果。自20世紀70年代以來，高速滾動軸承的動態性能特別是保持架的不穩定性問題就引起了人們的重視，并且一直是研究的熱點、難點。Walters[2]最早建立了球4自由度，保持架6自由度的球軸承動力學模型，模型中考慮了潤滑的影響但對球的運動進行了約束。Kannel等[3]建立了保持架平面運動的角接觸球軸承動力學模型，詳細分析了球與保持架的摩擦、潤滑劑黏度及球與滾道彈流潤滑拖動性對保持架運動穩定性的影響。Gupta[4]詳細分析了球與滾道，保持架與球及套圈擋邊的相互作用，建立了滾動軸承完全動力學模型，可以模擬時變工況下軸承零件的瞬態運動特性。Meeks等[5]對動力學模型進行了簡化，球的運動和載荷分布由擬靜力學結果確定，只需求解保持架的運動微分方程，從而提高了計算效率，并以球與保持架兜孔的摩擦功耗和碰撞力峰值為準則，對保持架兜孔和擋邊間隙進行了優化分析。與此同時，Gupta等[6]通過對球的平衡約束消除球與滾道的高頻彈性振動，從而增大積分步長，提高計算效率，并能夠有效地研究保持架的低頻特性。在此模型基礎上，Gupta[7-9]系統研究了工況、幾何、摩擦等因素對保持架穩定性的影響，對滾動軸承的性能優化具有重要參考價值。在過去的幾十年里，滾動軸承動力學模型不斷發展完善，越來越貼近實際工況，對保持架幾何缺陷、結構不對稱、柔性體化的仿真都已成為可能[10-13]。國內對滾動軸承動力學的研究近些年才有較快發展，主要采用兩種方法研究保持架的動態特性：一種是以Gupta模型為基礎，開發的滾動軸承動力學分析程序[14-15]；另一種是以通用多體動力學和有限元軟件為平臺進行仿真分析[16-18]。Liu等和Ye等課題組分別開發了高速滾動軸承動力學分析程序，但主要針對充分供油的航空發動機主軸軸承，結合具體算例探討了工況和幾何參數對保持架穩定性的影響。保持架不穩定運動的試驗研究相對較少。Kingsbury[19]首先分析了配對角接觸儀表球軸承摩擦力矩的擾動和保持架的運動，指出保持架的渦動是球與保持架摩擦耦合的結果，導致了摩擦力矩的低頻擾動；Kingsbury等[20]后來對儀表球軸承穩定運轉時和發生嘯叫時保持架的運動進行了試驗研究，發生嘯叫時，發現保持架在隨球組旋轉運動的基礎上有高頻的渦動，渦動頻率與球的自旋速率有關。

綜上所述，文獻中所討論的工況、幾何、摩擦等因素對保持架穩定性的影響都是間接的，而保持架的運動是由保持架與球及套圈擋邊的相互作用決定的。套圈擋邊平衡球對保持架的作用力及保持架的離心力，起到約束保持架不穩定運動的作用。據此推斷，保持架的不穩定運動主要與球的作用有關。本文以慣性儀表中支承高速轉子的角接觸球軸承為研究對象，建立球軸承動力學磨損數值仿真模型，分析不同工況下保持架的運動，試圖從球與保持架兜孔碰撞點的位置、碰撞力的大小和頻率以及碰撞點切向力的方向闡釋保持架不穩定運動的機理。

1 模型建立及程序校驗

1.1 高速儀表轉子軸承動力學模型的建立

根據Gupta研究中的滾動軸承動力學建模方法，建立了高速儀表轉子軸承動力學磨損數值仿真模型。模型中假定軸承組件的質心與幾何中心重合；球和保持架具有6個自由度，外圈質心固定，內圈質心具有3個自由度；潤滑的影響通過設定合理的摩擦系數來考慮，對于含油保持架自給潤滑的儀表球軸承，不考慮球與保持架及保持架與套圈擋邊之間的流體動壓作用；所有接觸按Hertz彈性接觸和Coulomb摩擦計算法向力和切向力。利用變步長四階Runge-Kutta法求解軸承的運動微分方程。模型簡要介紹如下，詳細的建模過程參考文獻[21-22]。

1.1.1 坐標系定義及運動學方程

軸承零件的質心運動在慣性坐標系中描述，繞質心的轉動在定體或方位坐標系中描述。坐標系定義見圖1。慣性坐標系原點Oi位于外圈溝曲率中心軌跡圓的圓心，Xi沿軸承軸向，Zi垂直向上。方位坐標系原點Oa固定于球心，Xa沿軸承軸向，Za軸徑向外指，其中dm為軸承節圓直徑，ψ為球的方位角。保持架坐標系原點Oc固定于保持架幾何中心，Xc沿保持架軸向，Zc指向第一個兜孔中心。

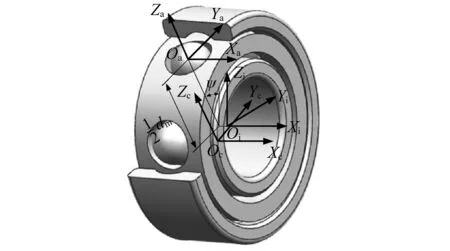
圖1 坐標系定義Fig.1 Coordinate system

從慣性坐標系到定體坐標系的轉換可通過三次相繼的旋轉實現，轉換矩陣為

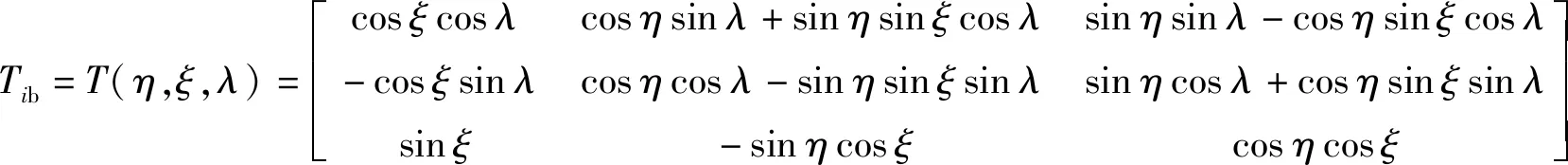
(1)

Gupta推導了軸承零件角速度與旋轉角 (η,ξ,λ)之間的關系，得到如下運動學方程

(2)

式中:(ω1,ω2,ω3)為軸承零件角速度分量。

1.1.2 平衡約束及運動微分方程

圖2 載荷作用前后角位置ψj處球中心和溝道曲率中心的位置Fig.2 Positions of ball center and raceway groove curvature centers at angular position ψj with and without applied load

為消除球與滾道之間彈性接觸引起的高頻振動，并能有效地研究保持架的低頻特性，模型中對球的運動采用了平衡約束。即在每一時間步，球心的軸、徑向運動微分方程由球與滾道的法向力平衡方程代替。球心的位置在慣性圓柱坐標系中描述，其軸、徑向位置由平衡方程確定。角位置ψj處球受到的作用力如圖3所示，球的平衡約束方程為

Qijsinαij-Qojsinαoj=0

Qijcosαij-Qojcosαoj+Fcj=0

(3)

式中：Qij,Qoj為球與內、外圈的法向接觸力，其中下標i,o指內、外圈。Fcj為球的離心力。圖3中，Fitxj,Fityj為內圈作用于球上的切向力，Mgj為陀螺力矩，Qcj為保持架與球的碰撞力。

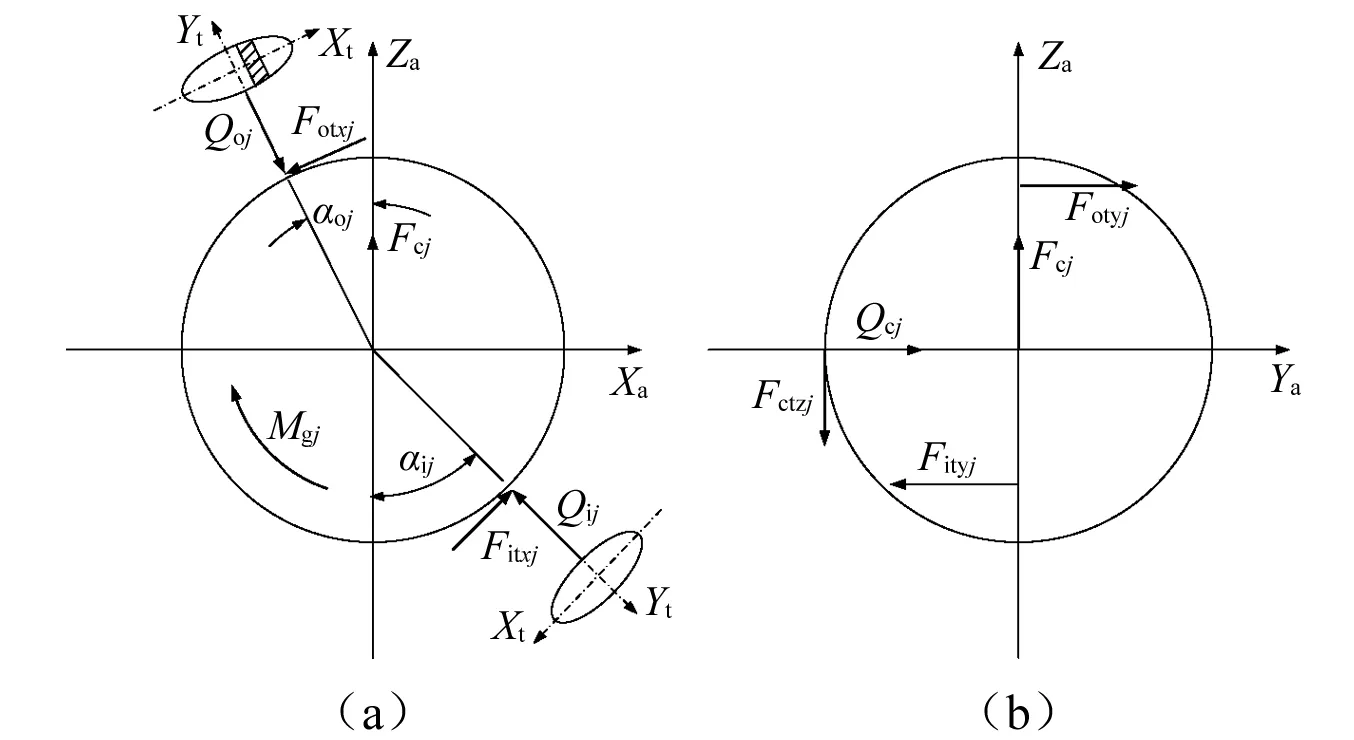
圖3 角位置ψj處球上的作用載荷Fig.3 Ball loading at angular position ψj

內圈質心的位置同樣由平衡方程確定，內圈質心具有3個自由度，其平衡方程為

(4)

式中：Fx,Fy,Fz為作用于內圈的軸向、徑向外載荷；N為球數。

由于球與滾道的切向力相對法力較小，為提高計算效率，平衡方程中未考慮切向力。

球心的軸、徑向位置及內圈質心位置由以上平衡方程聯立求解確定，球心在圓周方向的位置由微分方程式(5)確定。球的質心運動和動量矩方程為

(5)

(6)

保持架的質心運動和動量矩方程為

(7)

(8)

由質心運動方程和動量矩方程，與Gupta運動學方程聯立求解，即可描述軸承零件的一般運動規律。

1.1.3 軸承零件時間平均磨損率的計算

對于高速角接觸球軸承，球與滾道之間存在差動滑動、自旋滑動和陀螺滑動，且保持架與球及套圈擋邊之間也存在較大滑動，接觸區摩擦發熱和磨損不可避免。根據Archard黏著磨損理論公式[23]

(9)

式中：w為零件的磨損率；K為Archard磨損系數；H為材料的布氏硬度；Q，V分別為載荷和滑動速度。對球與滾道的接觸，接觸橢圓短軸一般較窄，滑動速度沿短軸的變化可以忽略。因此將橢圓接觸區沿長軸等距條形劃分，如圖4所示。分別計算各窄條上等效載荷和滑動速度的乘積QkVk，然后求和得到整個接觸區內QV值，代入上述公式計算磨損率。對于球/保持架及保持架/引導套圈的相互作用，由于滑動速度較大且接觸區較小，可以作為點或線接觸來計算瞬時磨損率。得到了任意時刻的瞬時磨損率，即可計算時間T內的平均磨損率

(10)

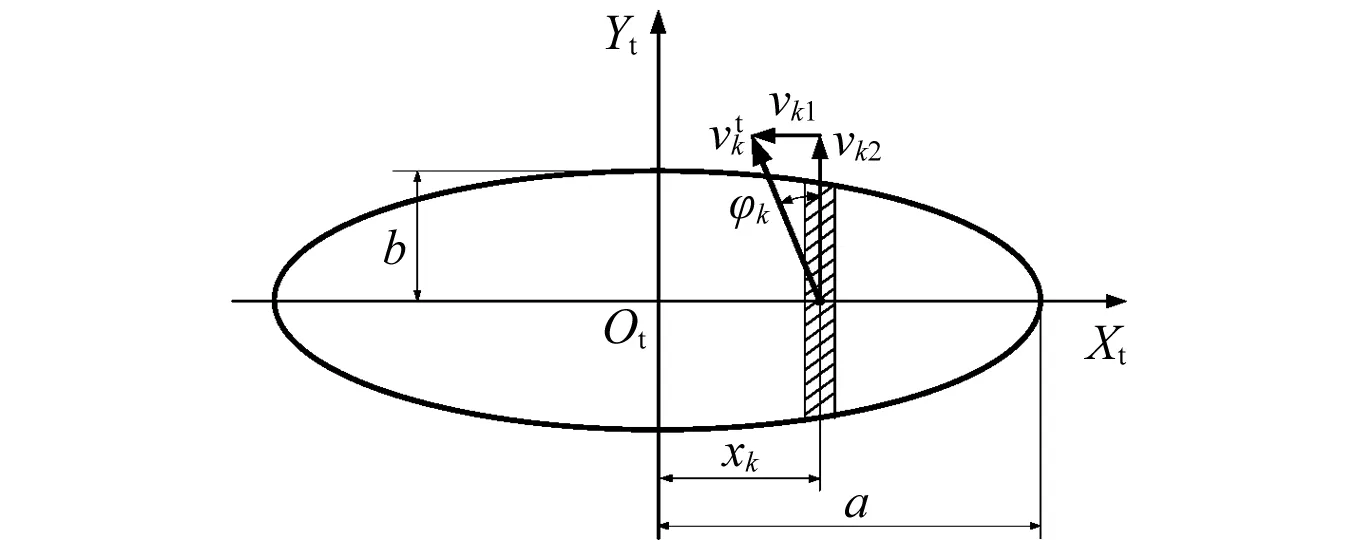
圖4 接觸橢圓內窄條中心處的滑動速度Fig.4 Sliding velocity in the contact ellipse

時間平均磨損率綜合反映了零件間相互作用力的大小和頻率，可以作為保持架穩定性定量判斷的依據。

1.2 動力學程序框圖及校驗

根據上述動力學模型，編寫了角接觸球軸承動力學磨損數值仿真分析程序。圖5所示為程序流程圖。

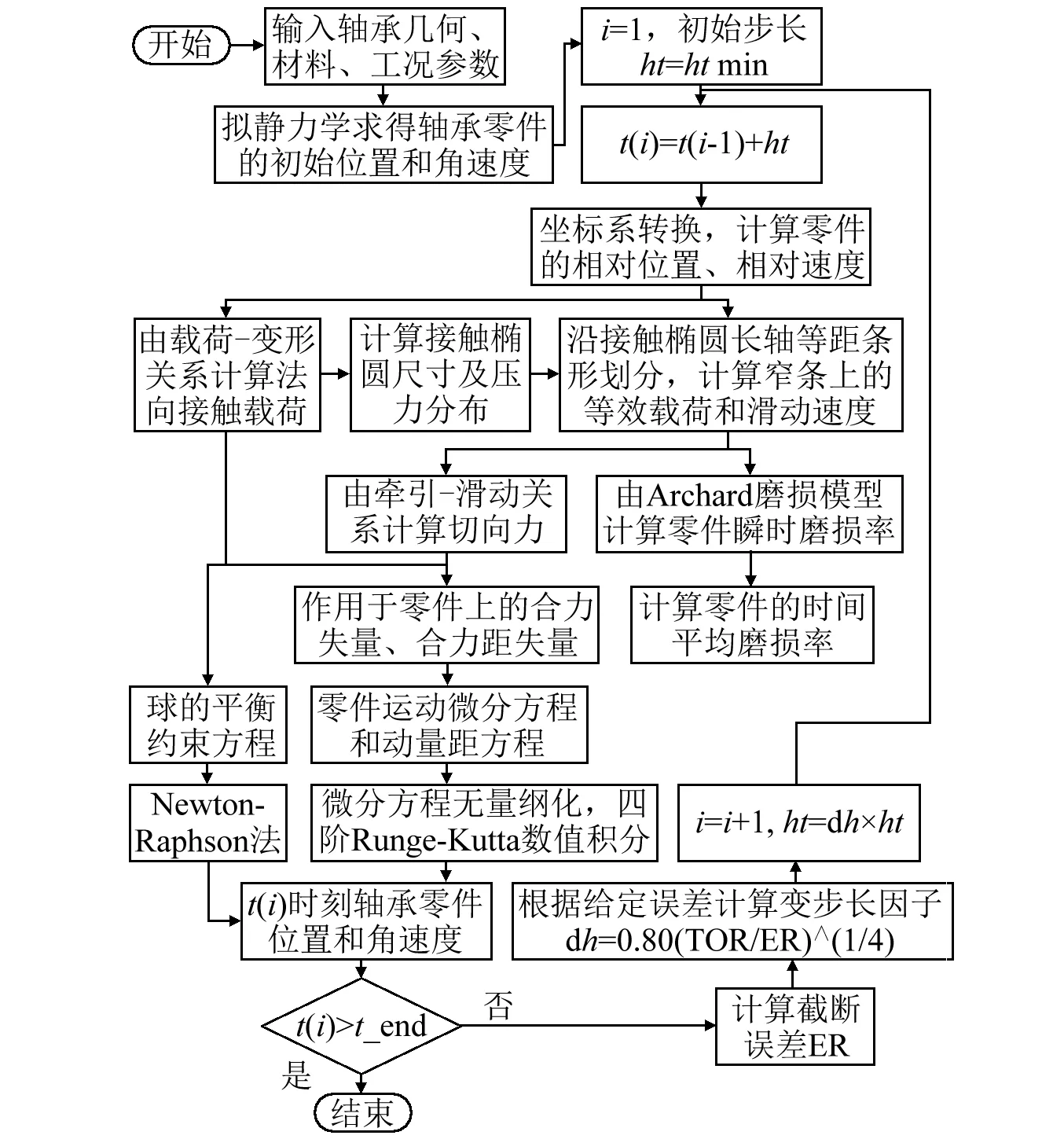
圖5 角接觸球軸承動力學磨損數值仿真程序框圖Fig.5 Flow chart of the dynamic wear simulation program of angular contact ball bearings

與Gupta研究中2號角接觸球軸承算例對比校驗球和保持架的時間平均磨損率，與3號角接觸球軸承算例的仿真和試驗結果對比校驗保持架的質心運動。圖6所示為保持架和球(No.1指初始時刻方位角ψ=0)的時間平均磨損率可以看出，本文結果與Gupta滾動軸承動力學分析程序ADORE的仿真結果變化趨勢一致，數量級一致，數值上也較為接近。圖7所示為保持架質心運動軌跡，本文結果與Adore仿真結果及Gupta試驗結果相吻合，保持架質心渦動半徑約等于保持架/套圈的徑向半徑間隙。以上對比驗證了本文程序的正確性、可靠性。

圖6 球與保持架的時間平均磨損率Fig.6 Time-averaged wear rates of ball and cage

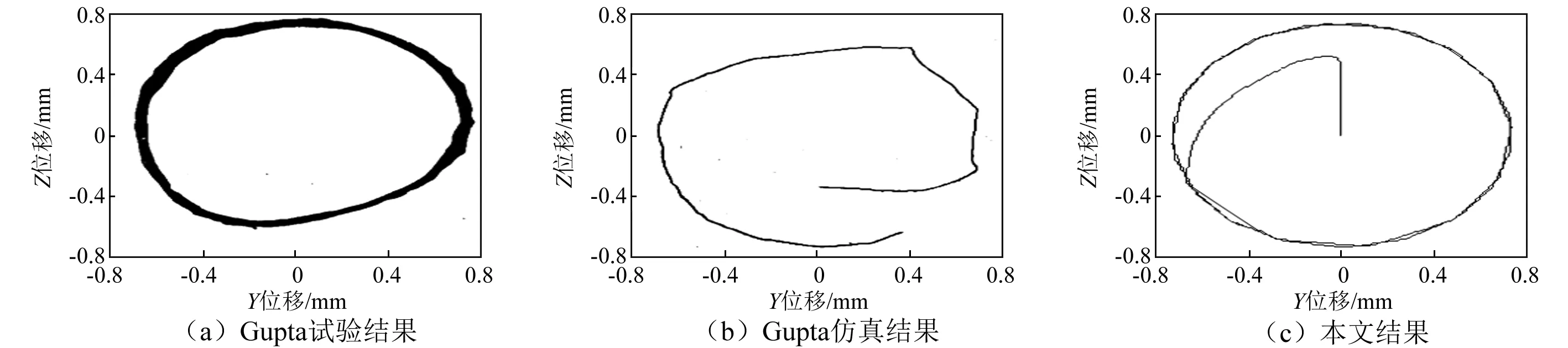
圖7 保持架質心運動軌跡Fig.7 Orbits of cage mass center

2 結果與分析

利用已校驗的程序，以某儀表轉子軸承為算例，分析了不同載荷工況和保持架間隙比下保持架的運動。深入研究了球與保持架兜孔碰撞點角位置、碰撞力的大小和頻率以及碰撞點切向力的方向對保持架不穩定運動的影響。保持架間隙比定義為球/保持架兜孔間隙(B)與保持架/套圈擋邊間隙(R)之比，如圖8所示。球與保持架兜孔碰撞點角位置的定義見圖9。軸承結構和材料參數列于表1。根據Archard磨損公式，時間平均磨損率與磨損系數成正比，目前程序引用文獻[23]中的磨損系數計算得到磨損率的變化趨勢。根據文獻[24-25]中拖動系數與油膜參數的關系，對含油保持架自給潤滑軸承計算得球與滾道的拖動系數為0.11，保持架與球及引導擋邊的摩擦系數設為0.05。

2.1 不同載荷工況的結果

某儀表轉子軸承的工況為，軸向預緊載荷7 N，內圈轉速30 000 r/min。為便于對比分析，假定由于轉子重力產生的徑向載荷為5 N，轉子質心偏移產生的旋轉徑向負荷也為5 N。分析得到了純軸向載荷、軸向徑向聯合載荷以及軸向旋轉徑向聯合負荷下保持架的質心運動軌跡，球與保持架的角速度，球與兜孔碰撞點角位置、碰撞力及保持架兜孔的磨損率，結果如圖10所示。

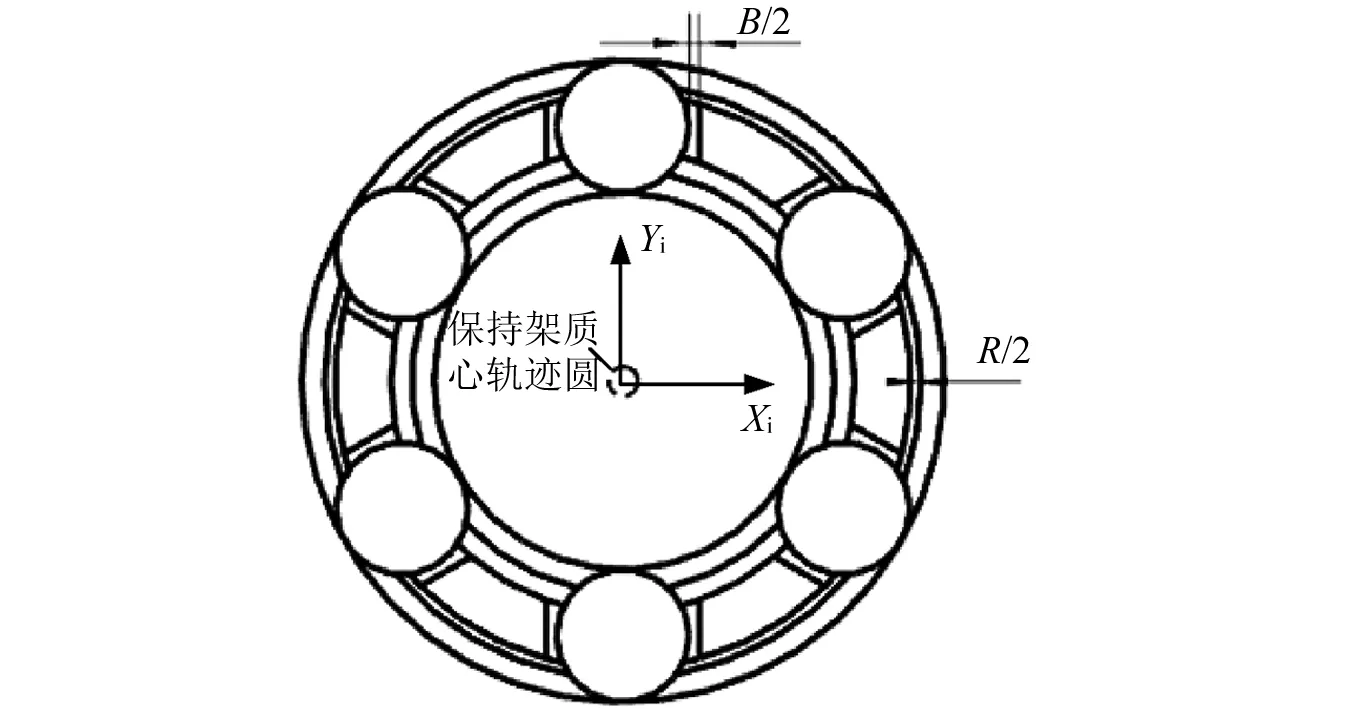
圖8 保持架間隙Fig.8 Cage clearance

圖9 球與保持架兜孔碰撞點角位置Fig.9 Angle position of ball and cage pocket collision

表1 軸承幾何和材料參數Tab.1 Bearing geometry and material properties

表1 軸承幾何和材料參數(續)Tab.1 Bearing geometry and material properties

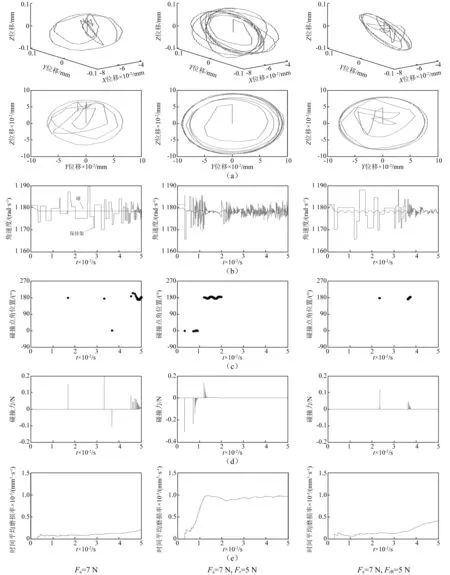
圖10 不同載荷工況下的結果比較Fig.10 Results under different load conditions

圖10(a)所示為保持架質心三維和二維軌跡圖。可以看出在軸向載荷下，保持架質心運動不在徑向平面內，軸向方向上有擺動，并趨于繞軸承中心穩定渦動，渦動半徑約等于保持架兜孔直徑間隙的一半。在軸向徑向聯合載荷下，保持架質心軸向擺動明顯，質心渦動半徑較大，說明保持架運動不穩定。軸向和旋轉徑向負荷下，保持架質心運動有偏斜，達到穩定渦動時的軌道半徑比兜孔半徑間隙稍大，是因為在徑向載荷下，球組中心偏離軸承中心，保持架中心隨之偏移，在離心力的作用下產生穩定的渦動，球組的徑向位移加上保持架的離心力使保持架的渦動半徑增大。

圖10(b)所示為1#球軌道角速度和保持架自轉角速度。由于保持架隨球組轉動，其角速度約等于球的軌道角速度，軸承運轉過程中球與保持架的無規律碰撞導致保持架的角速度頻繁波動。在軸向載荷下，球的公轉速度恒定，球與保持架碰撞較少；軸向徑向聯合載荷下，球的公轉角速度隨接觸角呈現周期性的變化，進入徑向載荷區球的轉速升高，而離開徑向載荷區時球的轉速降低，由于球在轉動過程中存在加速減速過程，導致球與保持架的碰撞較為頻繁，保持架的角速度也波動較大。參數化仿真的結果表明，在徑向載荷區和非徑向載荷區球公轉速度的變化不一定，球的轉速也可能會在徑向載荷區降低，而在非徑向載荷區升高。根據Harris在套圈控制假設下推導的球公轉角速度與套圈速度之比的公式，通過定性分析可得知：外滾道控制條件下，內滾道旋轉的軸承，球進入徑向載荷區轉速降低，而離開徑向載荷區時轉速升高；內滾道控制、外滾道旋轉的條件下，球的公轉速度有相同的變化規律，而在其它條件下，球的公轉速度變化不定。以上分析與動力學的結果相吻合，說明角接觸球軸承在聯合載荷作用下，球的公轉速度的變化不一定是通常認為的載荷增大轉速升高，載荷減小轉速降低，還與接觸角、旋滾比和轉速等因素有關。需要注意的是，雖然球的公轉速度隨接觸角周期性變化，但幅度其實很小，為0.085%。在軸向、旋轉徑向負荷共同作用下，球的公轉速度的變化周期減小，由于幾何和工況因素的耦合，球與保持架的碰撞也較少，保持架角速度波動的大小和頻率均減小。

圖10(c)所示為1#球與保持架兜孔碰撞點角位置，碰撞點角位置在0°或180°上下波動，即球滯后或超前保持架的運動。碰撞點在0°附近時，保持架推球，在180°附近時球推保持架。純軸向載荷下，由于保持架重力和離心力的作用，各球在保持架兜孔中的前后位置也會不同。球與兜孔碰撞點的滑動速度分量產生對保持架的軸向力，不同兜孔碰撞點處產生的軸向分力形成力偶作用于保持架，從而使保持架沿軸向發生擺動。軸向載荷下球在徑向平面內運動，球與保持架兜孔碰撞點的位置因保持架的擺動而在0°或180°附近變動。在軸向徑向聯合載荷作用下，因接觸角的變化，球在不同角位置處有微小的軸向位移(與保持架兜孔間隙相差兩個數量級)，加上保持架本身的擺動，導致了球與兜孔碰撞點角位置在0°或180°上下波動。

圖10(d)所示為1#球與保持架兜孔的碰撞力。可以看出在軸向徑向聯合載荷下，碰撞力較大，頻率也較高，是因為在徑向載荷下球有加速和減速過程，各球的轉速不一致導致球與保持架更容易碰撞。而在旋轉徑向載荷下，由于保持架的渦動與球的轉速的耦合，使球與保持架的碰撞較少。

圖10(e)所示的保持架時間平均磨損率是所有兜孔的磨損率。因為是球引導保持架，保持架與套圈擋邊沒有碰撞，磨損主要發生在兜孔上。純軸向載荷下保持架的磨損率最小，軸向徑向聯合載荷下保持架的磨損率最大，此時對應保持架的運動最不穩定，質心軌跡擺動較大，且軌道半徑發散。保持架的時間平均磨損率綜合反映了球與保持架碰撞力的大小和頻率。

2.2 不同間隙比的結果

球與保持架兜孔間隙和保持架引導面與套圈擋邊間隙是影響保持架穩定性的重要設計參數。通常用兜孔間隙與擋邊間隙之比B/R進行參數化分析，得到最優的保持架結構參數。不同的間隙比對應不同的保持架引導方式，一般地B/R<1時為球引導，B/R=1時為球與套圈混合引導，B/R>1時為套圈引導。對于轉速較高的儀表轉子軸承，當轉子中心與支承中心不重合或轉子質心偏移時會產生較大的慣性負荷，相當于對軸承施加一個旋轉徑向負荷。轉子質量一般較小(50 g)，重力產生的徑向力可以忽略，軸向預緊載荷加旋轉徑向負荷是高速儀表轉子軸承典型的工況。根據某儀表轉子軸承的實際工況，軸向預緊載荷7 N，內圈轉速30 000 r/min，旋轉徑向負荷假定為5 N。在該工況下分析了不同間隙比對保持架的運動、碰撞和磨損的影響，結果如圖11所示。

圖11(a)所示的保持架質心運動軌跡可知，當兜孔間隙小于擋邊間隙即球引導保持架時，保持架的質心運動軌跡接近于圓形，隨著間隙比的增大，保持架的質心軌跡由圓形變為多邊形直至無規律的渦動，軌跡半徑隨之減小。說明球引導保持架時有利于形成圓形的渦動軌跡，套圈引導保持架時容易形成多邊形的渦動軌跡。

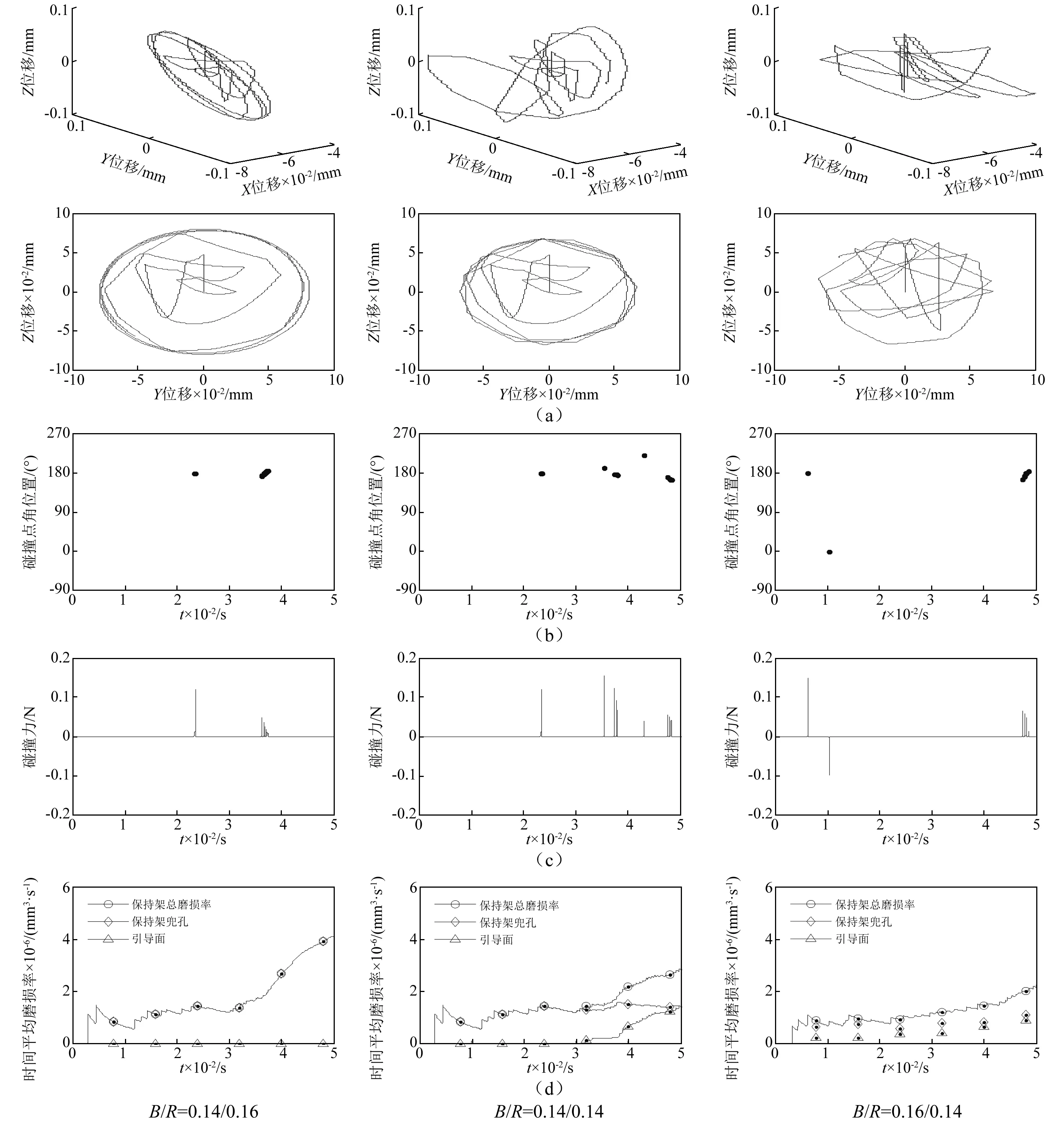
圖11 軸向旋轉徑向負荷下不同間隙比的結果Fig.11 Results of different clearance ratio under combined axial and rotating radial load

圖11(b)中，間隙比為1時球與保持架兜孔碰撞點角位置范圍最大，說明保持架的軸向擺動較大，兜孔間隙較小時，保持架由球引導，保持架的離心力主要作用于球上，限制了保持架的自由擺動；而當兜孔間隙較大變為套圈引導保持架時，保持架的離心力主要作用在套圈擋邊上，球與保持架的相互作用減少，保持架的擺動幅度又減小。因此，保持架由球與套圈擋邊共同引導時，保持架容易發生擺動。

圖11(c)所示的1#球與保持架兜孔的碰撞力可以看出，間隙比為1時，球與兜孔的碰撞較為頻繁，兜孔間隙增大，碰撞力的大小變化不明顯，相對于球引導，套圈引導時，球與兜孔的碰撞力稍大。

圖11(d)給出了不同間隙比下保持架兜孔和引導面的磨損率分布。單看保持架兜孔的磨損率，球引導時保持架兜孔的磨損率最高，兜孔間隙增大，兜孔的磨損率降低，而保持架引導面的磨損率升高。保持架兜孔和引導面總的時間平均磨損率可以看出，隨著間隙比的增大，保持架的總磨損率降低。這是因為球引導保持架時，保持架質心沿圓形軌道渦動，保持架的離心力作用于球上，增大了球與保持架兜孔之間的碰撞和摩擦。保持架由套圈擋邊引導時，保持架質心沒有形成穩定的渦動，其離心力較小，且有套圈擋邊對保持架運動的約束會減小球與兜孔的相互作用，所以保持架兜孔和總的磨損率都較低。需要注意的是，圖中所示為1#球與保持架兜孔的碰撞情況，保持架兜孔的磨損率為所有兜孔總的時間平均磨損率。

以上分析可以得出，保持架質心運動軌跡與兜孔磨損率存在對應關系。保持架質心運動軌跡為圓形且軌道半徑發散，對應的兜孔磨損率較大；保持架質心軌跡呈多邊形或不規則渦動且渦動半徑較小時，保持架兜孔的磨損率減小。因此，從保持架磨損和能耗的觀點看，圓形的質心運動軌跡未必最優。保持架質心運動軌跡越圓，說明質心渦動速度的大小穩定，波動小，但保持架渦動速度的方向不斷變化，這也說明保持架與球有頻繁的相互作用。保持架質心運動軌跡為多邊形或無規律渦動時，雖然質心渦動速度變化較大，但球與兜孔碰撞較少，而碰撞力沒有明顯變化，所以保持架兜孔的磨損率較小。Meeks等分別以球與兜孔碰撞力和磨損能耗最小為準則，對保持架幾何參數進行優化的結果也表明，保持架兜孔間隙與擋邊間隙之比大于1時是有利的，此時對應的保持架質心運動軌跡是隨機的。因此，對高速角接觸球軸承保持架結構參數進行優化時，不能單純追求保持架質心運動軌跡為圓形或渦動速度穩定，應結合球與保持架兜孔的碰撞力和磨損功耗進行綜合優化。

3 結 論

利用建立的高速角接觸球軸承動力學磨損數值仿真模型，分析了不同載荷工況和保持架間隙比下保持架的質心運動。從球與保持架兜孔碰撞點位置、碰撞力的大小和頻率以及碰撞點切向力的方向闡釋了保持架不穩定運動的機理。在給定的軸承幾何、工況和潤滑條件下，通過動力學仿真研究得到如下結論：

(1)純軸向載荷下，由于保持架重力和離心力的影響，各球與保持架碰撞點的位置不同，碰撞點沿軸向的切向分力組成的力偶作用于保持架引起了保持架的軸向擺動。

(2)軸向、徑向聯合載荷下，球的公轉角速度隨接觸角呈現周期性變化，但幅值較小，為0.085%。球進入和離開徑向載荷區公轉速度的變化與接觸角、旋滾比和套圈轉速有關。由于球公轉一周有加速減速過程，導致球與保持架的運動不協調，容易發生碰撞，保持架的角速度波動頻率較高。軸向、旋轉徑向聯合負荷下，球的公轉速度的變化周期減小，由于幾何和工況因素的耦合，球與保持架的碰撞減少，保持架角速度的波動頻率也減小。

(3)軸向、旋轉徑向聯合負荷下，保持架兜孔間隙與引導面間隙之比B/R<1時，保持架質心運動軌跡接近于圓形，因為球引導保持架，保持架的離心力作用于球上，增大了球與保持架兜孔之間的碰撞和摩擦，保持架兜孔的磨損率較大；B/R=1時，保持架由球與套圈擋邊共同引導，保持架質心軌跡呈多邊形，保持架的軸向擺動較大，球與兜孔的碰撞頻率也較高；B/R>1時，套圈引導保持架，球與保持架的相互作用減少，保持架質心渦動不規則，但球與兜孔碰撞力沒有明顯增大。

(4)保持架質心運動軌跡與兜孔磨損率存在對應關系，質心運動軌跡為圓形是保持架穩定運動的一種狀態，但對保持架的磨損壽命不利。以保持架磨損和能耗為優化準則時，B/R>1是較優的選擇。保持架兜孔的時間平均磨損率綜合反映了球與兜孔碰撞力的大小和頻率，可以作為保持架動態性能優化和穩定性判斷的準則。