基于Lamb波遞歸量化分析的復合材料裂紋損傷定征研究

劉小峰，楊康俊，柏 林

(重慶大學 機械傳動國家重點實驗室，重慶 400044)

復合材料層合板具有質量輕、成本低、比強度和比模量高等諸多優點，被廣泛應用于航空航天產業和其它高新技術領域的同時，也給其基體微裂紋損傷和分層損傷的無損檢測帶來了挑戰。在外力的作用下，基體微裂紋會引起層間應力集中，并隨著微裂紋數量的增加，導致界面應力增加產生脫粘，顯著降低了復合材料的壓縮強度和剛度，而脫粘的擴展產生分層會導致最終結構的總體失效。Lamb波檢測技術通過主動激發應力波對結構內部進行檢測，可有效地感知粘接界面的變化，具有快速、長距離、大范圍、成本相對低的特點，其在復合材料檢測領域得到廣泛應用[1]。但目前大部分基于Lamb波的復合材料板損傷檢測主要集中在分層、孔或狹縫等后期嚴重損傷的檢測與辨識方面[2]，而對復合材料早期出現的基體微裂紋的檢測研究的文獻還相對較少。Toyama等[3]研究了Lamb波速度如何受到基體微裂紋和分層的影響，卻沒有給出具體的檢查方法。文獻[4]采用了機器學習方法對基體微裂紋和分層的分類辨識進行了的初步研究，但未給出基體微裂紋的定量表征方法。文獻[5]采用高斯判別方法對復合材料板中常規微損傷程度進行了分別識別，但尚未涉及基體微裂紋的損傷程度辨識。因此，對基體微裂紋的檢測與定征研究對保證復合材料板的安全可靠的服役具有重要的研究意義。

復合材料的細觀構造是一個復雜的各項異性多相體系，同時還具有較高的聲衰減率，導致獲取的Lamb波信號中噪聲與損傷反射信號互相混雜，損傷信號波形不易分辨，信噪比低，這都給信號處理與損傷識別、定量評價帶來了一定的困難。目前大多數Lamb波損傷特征提取方法都是基于平穩信號分析的時域或頻域特征提取，而不同程度的基體微裂紋所引起的信號的特征在時域與頻域上的差別不明顯，再加上反射、散射波、模態轉換波及噪聲的影響與干擾，使得獲取的Lamb波響應信號必然會表現出較強的非線性性、不確定性與復雜性。傳統的Lamb波信號處理方法特征對微損傷程度缺乏足夠的敏感性。目前的損傷波包識別方法[6-7]都缺乏損傷識別的可靠性、準確性、分析處理的快速性、惡劣檢測環境的適應性。

針對以上問題，本文創新性地采用遞歸分析方法對復合材料的微損傷進行定征分析，并結合各項遞歸定量分析指數定義了復合材料損傷的統一表征指數UDI(Uniform Damage Index)，該指數對復合材料早期基體微裂紋損傷具有較好的敏感性，與損傷程度成良好的線性關系，為復合材料的損傷檢測提供了一個有效可行的方法與手段。

1 遞歸圖

遞歸圖為揭示時間序列內部隱含的非線性系統內部信息提供了有效的定性分析方法。在狀態空間內分析系統的動力學系統，確定系統的運動狀態，就可以對系統進行完整的描述。在Lamb波對復合材料板進行無損檢測時，可將Lamb波在板中的傳播看作一個動力系統，這個系統是建立在Lamb波傳播特性的基礎上的，有許多可以描述其狀態的變量，所有的這些變量可以支撐系統的相空間和狀態空間。系統的狀態會隨著時間變化，其相應的Lamb波信號也展現出復雜的動力學行為。

當損傷尺寸較大，如基體微裂紋數目增多，嚴重分層時，這類損傷反射回波能量較大，其相應Lamb波信號的動力學非線性增強，導致其表現出來的遞歸特性有所不同。也就是，可將損傷狀態下獲得的Lamb波信號看作一個確定性的非線性動力系統，即可由該信號序列反推得到復合材料板損傷狀態下的復雜的非線性動力系統。材料內部各個損傷間的多次散射、反射使得Lamb波的非線性特性增強，且內部損傷的發生具有明顯隨機性和不確定性。

遞歸圖具有對演化規律的敏感性，因此每一種特征翻譯了系統不同的演化規律，對于有限長度的信號而言則可以揭示信號內在的變化規律。如果復合材料板內部存在的基體微裂紋損傷增多，將導致反射與散射的Lamb波增加，而Lamb波反射及散射方向是多變的，考慮到超聲換能器的位置和方向是固定的，因而可認為接受到的Lamb波信號的強度會隨著裂紋的存在而改變，強度上可能變大也可能變相；另外基體微裂紋的分布具有較強的隨機性，導致回波信號的隨機成分增加，損傷對Lamb波的傳播過程的影響具有顯著的非線性特征，這從理論上支持了可以使用遞歸分析對Lamb波信號進行評價。

Lamb波信號的量化遞歸分析是利用損傷信號的混沌特性，分叉特征，子相似性及確定性，對復合材料板損傷狀態下的結構動力學特性進行描述，從而達到對其內部損傷定征的目的。通常情況下，可以用相空間中的一個“點”來表示動態系統在該時刻的狀態，對于d維動態系統在固定時刻t的狀態可以用式(1)所示的向量來表達

(1)

這樣的“點”稱為相點。若該系統是一個連續時間系統，則其隨時間的演化規律可以式(2)中的微分方程來表達，這樣相點隨時間的演化即在相空間中即構成了相軌跡。

(2)

有限的Lamb波時間序列，通過這些時間序列回復出結構系統相軌跡的幾何結構并保持其基本性質，這就是相空間重構。根據Takens定理，對一個時間序列

X={yj|yj=[xj,xj+τ,…，xj+(m-1)τ]T}

(3)

式中：m為嵌入維數；τ為延遲時間；j=1,2,…,M,M=N-(m-1)τ為相空間中的相點個數。只要嵌入參數m和τ選取恰當，重構的相空間便于原系統相空間微分同胚。一般常選用互信息法[8]計算τ，用Cao[9]的方法計算m。遞歸圖的定義是以相空間重構為基礎的，它反映了重構后吸引子所具有的某種屬性，不同性質的信號，其吸引子的表現不一樣，遞歸圖的結構也不同。遞歸圖的數學表達式為

(4)

式中：Θ(·)為Heaviside階躍函數；Θ(x<0)=0,Θ(x≥0)=1；‖·‖為距離范數；ε為遞歸閾值。當相空間中任意兩點間的距離小于ε時，在遞歸圖上顯示為一白點，因此遞歸圖表現為黑白圖形來刻畫時間序列[10]。遞歸圖旨在顯示化分析高維動力系統的相軌跡，其模式與系統特定的動力學行為相關。

2 遞歸定量分析(Recursive Quantitative Analysis,RQA)

盡管遞歸圖能夠展現系統狀態隨時間演化過程中的遞歸行為，但卻無法對其進行定量描述。為了定量分析Lamb波信號中隱含的結構損傷信息，可采用遞歸量化指標[11]對遞歸圖中的遞歸特性進行表征。基于遞歸圖中遞歸點的密度，沿對角線紋理特征可定義如下5個參數指標，用以定量分析Lamb波激勵下的復合材料板振動系統的遞歸行為。

確定率(Determinism,DET)：指兩個以上的白點連成的對角線段在遞歸圖中所有白點中占得百分比，用于描述系統的確定性變化。

(5)

式中:l等于組成線段的白點個數，代表對角線程度，lmin=2;p(l)為長度為l的對角線段出現的概率。

遞歸熵(Entropy,ENTR):對角線段的香農熵，通常表示系統變化的不確定程度。

(6)

捕獲時間(Trapping Time,TT):遞歸點構成垂線或水平線段的長度，描述系統在某個特定狀態下的平均保持時間。

(7)

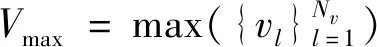
平均對角線長度(L)：代表兩段相軌跡在相空間中相互靠近的平均時間，即系統的平均可預測時間。

(8)

1型平均遞歸時間T1：反映了系統穩定性的程度，在重構相空間內，以參考向量點X0為中心，以臨界距離ε為半徑的球形區域內相應鄰域點的集合定義為1型鄰域點集合S1={Xt1,Xt2,…,Xti,…}，得到1型遞歸時間為{T1(i)=ti+1-ti,i=1,2,3,…}，取平均值即可得到1型平均遞歸時間T1。

(9)

式中：d1為系統的信息維數。

3 試驗驗證

3.1 疲勞循環實驗

本文選擇試驗對象為美國航天局復合材料疲勞循環實驗中的狗骨形復合材料層合板，其尺寸為15.24 cm×25.4 cm，鋪層方向為[02/904]s，如圖1所示。左端加工了一個凹槽，凹槽尺寸為5.08 mm×19.3 mm，經過加載和疲勞循環后，凹槽周圍出現了微小基體微裂紋損傷。每次循環加載完成后，采用X光對板材進行掃描，記錄其基體微裂紋的個數，具體信息如表1所示。

圖1 復合材料試驗板Fig.1 Composite test board

層合板上下布有12個傳感器，編號為1～12，如圖1所示，分別取傳感器1～6作為信號激發器，傳感器7～12作為信號接收器，共產生36組響應信號。激發信號是中心頻率為250 kHz的5周期的漢寧窗調制波，信號的采樣頻率為12 MHz，每組信號采集2 000個點,取前1 024個點。從圖1可知，路徑5～7，5～8，6～8，6～9非常接近或者通過損傷區域，其對應的Lamb波信號最大程度上地包含了層合板損傷信息。

圖2給出了工況1與工況6下，路徑6～8上采集的Lamb波信號的時域波形圖及其頻譜圖。從圖2可知，不同損傷程度下的接受的Lamb波信號的不管在時域波形上還是其頻譜成分上都極為相似。盡管可根據波包傳播速度及其散射能量的變化，以直達波包傳播時間及散射能量作為裂紋損傷程度的表征量，但這些時頻域的特征量與損傷程度并不存在著較好的線性關系，無法對損傷程度進行準確的量化識別[12]。再者，在一般工程應用中，往往會產生直達波包與其他散射波包、反射波包混疊的情況，再加上噪聲的影響，也會造成直達波包分離困難的問題。

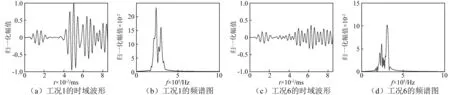
圖2 不同工況下路徑6～8上的Lamb波信號Fig.2 Lamb wave signal on path 6～8 for different conditions

3.2 遞歸圖分析

分別對表1中不同工況下的路徑5～8獲得Lamb波信號進行遞歸分析。首先計算所用響應信號的嵌入維數m與時間延遲τ，進而可計算得到圖3中的路徑5～8不同工況下的Lamb波信號遞歸圖。

從圖3可知，每種遞歸圖中的對角線分布并不相同，損傷程度大的情況的對角線的分裂較嚴重，并且白斑現象非常嚴重。這表明各路信號中反映的結構子相關特性與振動特性的各不相同。對角線代表了信號中固有的振動特性，各個子圖中的帶狀結構，對角線的粗細也各不相同，這表示每個信號中的周期特性，自相關性也各不相同。隨著微損傷個數的增加，遞歸圖越來越分散(見圖3)，在圖3(a)～圖3(d)4個遞歸圖中，遞歸點相對比較集中，圖3(e)～圖3(f)中的兩個遞歸圖中，遞歸點就明顯表現出分散性。可見，遞歸圖未包含任何線性變化，是一種基于概率、普遍的提取結構振動特性的方法，可以作為用于提取損傷造成的Lamb波信號非線性特征的有效工具。

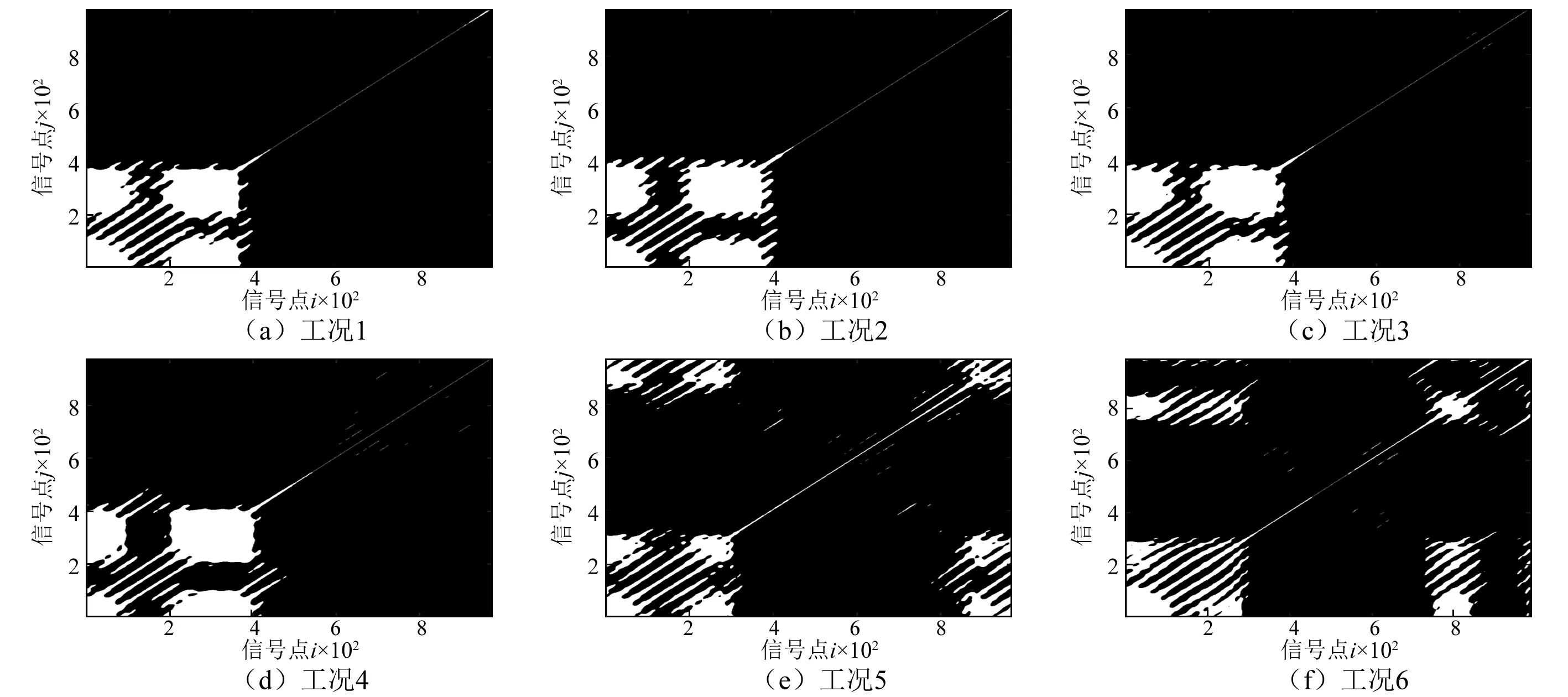
圖3 路徑5～8中6組信號的遞歸圖Fig.3 Recursive plots of 6 groups of signals in path 5～8

3.3 遞歸量化分析

遞歸分析主要是利用總結歸納得到的遞歸圖模式對一些簡單的信號特征做出判別，而遞歸量化分析使用了量化分析手段，更適用于分析多散射多模態等復雜的Lamb波信號。遞歸量化指標是根據遞歸點在遞歸圖上分布特征而計算得出的特征參數，根據式(5)～式(9)在遞歸圖基礎上得出的各種工況下各路信號的DET，ENTR，L，T1及TT值，如圖4所示。

隨著微損傷個數的增加，損傷信號增強，遞歸圖上的遞歸點數減少，信號整體的遞歸性下降，因此出現了DET隨損傷程度的增加而下降趨勢(見圖4(a))。隨著微裂紋個數的增加，Lamb波信號的信息量增加，損傷信號更加明顯，信號的不確定性減小，導致了ENTR的減小(見圖4(b))。

隨著微損傷個數的增加，接收的Lamb波信號的周期性越差，不同矢量之間的歐式距離會增大，相空間軌跡發散就越快，因此平均對角線L的長度越小(見圖4(c))。獲取的Lamb波信號的規律性降低，導致遞歸圖的分散程度增加，從而造成遞歸圖中垂直結構的平均長度減小，即TT的減小(見圖4(d))。由于微損傷個數增多，相應的損傷信號也會會增強，增強信號經過相空間重構后，原本在1型鄰域點集合內的重構向量會更靠近球邊緣，而原本在球外的重構向量會進入到球中，導致系統的狀態轉換時間變大,即T1的增大(見圖4(e))。由于試驗板的損傷程度不僅與微損傷個數有關，而且還與損傷分布方向與位置有關系，因此，圖4中RQA參數與損傷程度并不成完全的線性關系，但可用于表征試驗板的損傷程度的變化趨勢。

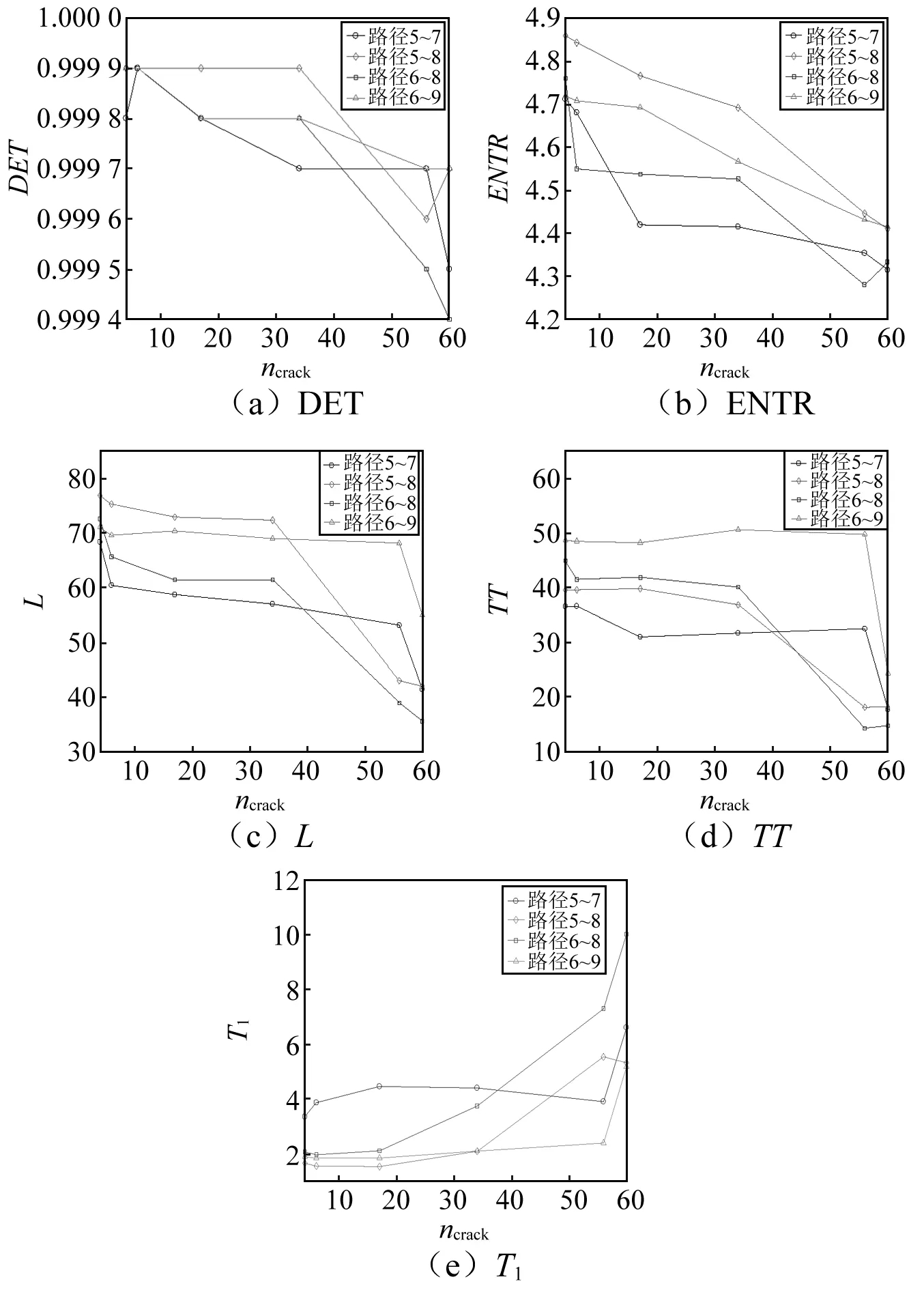
圖4 RQA參數隨損傷程度的變化趨勢Fig.4 Trends of RQA parameters changes with the degree of defect

3.4 特征融合

從圖4可知，不同的RQA特征參數對損傷程度的敏感度不同，魯棒性也各不同。為了統一表示復合材料板的損傷損傷狀態，有必要采用統一的融合指數對其損傷程度進行表征。由于表1中的工況1下的復合材料板近似可看作是無損狀態，因此可將工1況下測得的RQA特征量作為基準，以損傷狀態下的特征量與基準之間的偏差作為統一損傷指數，以表征試驗板的損傷程度。將圖4中的5個RQA表征參數進行歸一化后，取其與工況1下的特征參數的歐式距離作為融合的特征值。設工況i與工況j下的RQA參數組成的特征向量分別為

Xi=[xi1,xi2,xi3,xi4,xi5],Xj=[xj1,xj2,xj3,xj4,xj5]

(10)

xi1,xi2,xi3,xi4,xi5分別為工況i下的Lamb波響應信號的DET，ENTR，L，TT，T1的RQA特征值。則Xi與Xj兩者之間的歐式可表示為

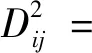
(11)

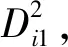
(12)

式中：α為無損與有損狀態間的閾值，這里取0.052。

從圖5可知，特征融合后的DI值與Larrosa等研究中的直達波包時域峰值，能量及功率譜密度峰值相比，其對基體微裂紋損傷的敏感程度明顯較大，隨著損傷個數的增加而成線性單調遞增的趨勢，更能對復合材料板的基體微裂紋損傷進行準確表征。但圖5中各個路徑上的DI-ncrack擬合直線的斜率各有不同，說明不同路徑上的DI值對損傷程度的敏感度并不一樣，越是靠近損傷區域的路徑6～8上得到的DI敏感性越好。由于實際工程應用中損傷位置未知的情況下，路徑的選擇存在非確定性，因此，有必要將各個路徑的DI值進行再次融合，得到試驗板的最后的UDI。路徑指數的融合方法如式(13)所示

(13)

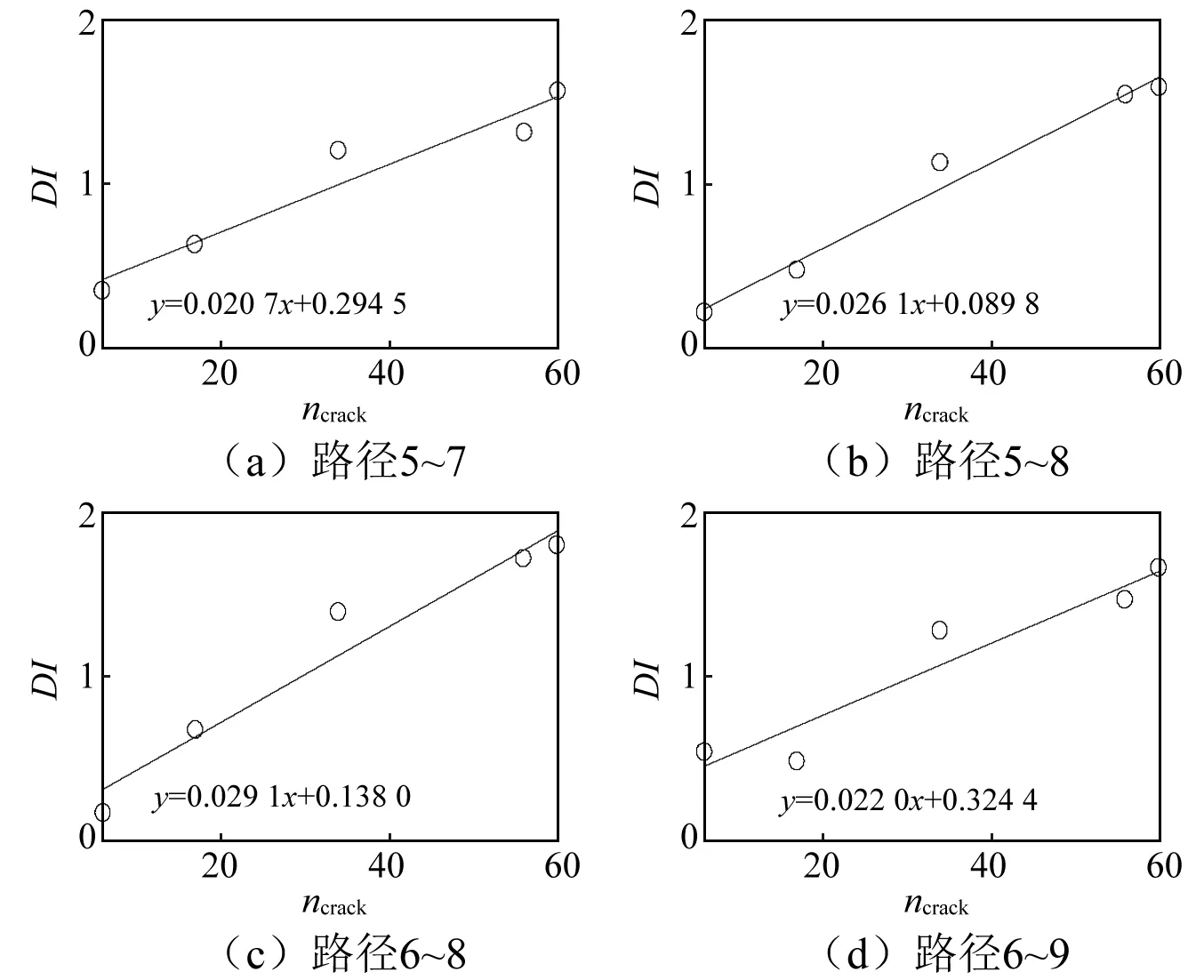
圖5 DI值隨微損傷個數的變化趨勢圖Fig.5 Trends of DI value changes with the number of micro-defects

式中：DIi=[DIi,5-7,DIi,5-8,DIi,6-8,DIi,6-9]，DIj=[DIj,5-7,DIj,5-8,DIj,6-8,DIj,6-9]分別為工況i與工況j下的各個路徑上的DI值所構成的損傷指數向量；DIik與DIjk分別為工況i與工況j下的第k條路徑中的得到的DI指數。在圖5的DI值的基礎上，采用式(13)得到的UDI值，如圖6所示。

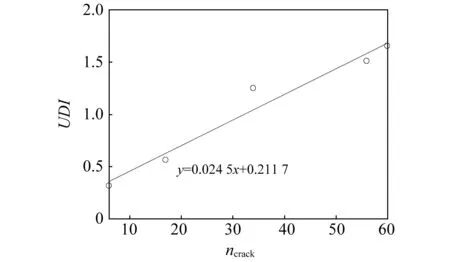
圖6 FDI隨微損傷個數的變化趨勢圖Fig.6 Trends of FDI changes with the number of micro defects

從圖6可知，將多路徑DI指數融合后，UDI隨微損傷個數的增加表現出單調線性遞增的趨勢。UDI與損傷個數的變化之比為0.024 5，說明UDI值對復合材料中的基體微裂紋損傷程度具有較好的敏感性，能格準確表征試驗板的損傷程度。

4 結 論

本文以Lamb波遞歸定量分析為基礎，分析討論了復合材料在不同疲勞循環次數下的基體微裂紋個數對應的損傷程度大小。為達到對復合材料板損傷進行統一描述，采用特征向量歐式距離將不同傳感路徑上的不同RQA指數進行了融合，提出了基體微裂紋損傷的UDI。分析結果表明，本文提出的UDI對復合材料基體微裂紋損傷具有較好的敏感性，與損傷程度成良好的線性關系，為復合材料的損傷檢測提供了一個有效可行的方法與手段。本文旨在發展一種基于量化回歸分析的Lamb波信號特征提取方法，建立信號特征與微裂紋損傷程度之間的映射關系，達到對復合材料板的基體微裂紋損傷進行定性定量檢測的目的。