多向地震作用下土-框筒結構動力響應試驗研究與數值模擬

沈 超，錢德玲，朱志鵬，葉瀟瀟，張恒源

(合肥工業大學 土木與水利工程學院，合肥 230009)

地震運動多呈現為水平和豎向的多向復雜震動。近幾十年的地震災害記錄表明，在震中地區，相比于單向水平震動，多向震動對建筑物的破壞更為嚴重。因此，高層建筑在多向地震作用下的動力性能研究，對建筑抗震設計具有十分重要的意義。

現有國內文獻大多僅研究了豎向地震作用對建筑物的動力性能的影響，多向地震作用下框架—核心筒高層建筑的動力性能方面的研究較為少見。張玉梅等[1]采用總參數法推導了考慮土—結構動力相互作用的高層框架結構在多向地震作用下的運動方程，經數值計算得到了結構的地震反應。周長東等[2]采用有限元軟件模擬了240 m鋼筋混凝土煙囪結構在多維地震作用下的動力反應并對結構進行了易損性分析。研究結果表明，相比于單向水平地震作用，多向地震作用下高聳煙囪結構的易損性和倒塌概率更大。何志軍等[3]對超大框筒結構的上海中心大廈進行了豎向地震反應計算和分析，結果表明豎向地震作用能夠增大結構的加速度反應，且幅值隨建筑高度增加而變大。國外學者在土—結構動力相互作用高層建筑抗震性能與動力特性方面也做了相關研究。Durmus等[4]采用有限元軟件對單自由度結構—土動力相互作用體系在地震作用下的動力反應進行了模擬，提出了與理論計算結果更為接近的簡化模擬方法。Badry等[5]通過有限元軟件模擬了群樁基礎框架結構的高層建筑在2015年尼泊爾地震作用下的動力特性。研究結果表明，同種工況下，SSI(Soil-Structure Interaction)模型上部結構的動力響應小于FB(Fix-Based)模型。

本文對上部結構為20層框架—核心筒結構的SSI和FB兩種模型進行了單向水平和多向地震作用下的動力響應研究。通過對比SSI模型在單向水平和多向地震作用下的水平方向動力響應，得到了多向地震對框筒結構水平方向抗震性能的影響；將多向地震作用下SSI和FB模型的豎向動力響應進行對比，分析了土對結構豎直方向動力響應的影響。研究成果可為高層建筑的抗震性能研究提供參考。

1 土—結構相互作用模型

1.1 模型的設計與制作

為使研究結果能夠更準確地接近實際建筑在多向地震作用下的動力特性，試驗模型選用某41層框架—核心筒高層建筑作為模擬對象。采用抽層的方法對原型結構進行簡化，將各樓層中相鄰上下樓板抽去，并將所抽去樓板的恒活荷載平均分配至相鄰上下樓板。同時，采用強度和剛度等效原理對柱和核心筒截面進行修正。最終將41層的原型結構簡化為了縮尺比例為1/50的20層試驗模型。采用Buckingham π定理確定相似比例，各相似比例如表1所示。抽層過程如圖1所示。

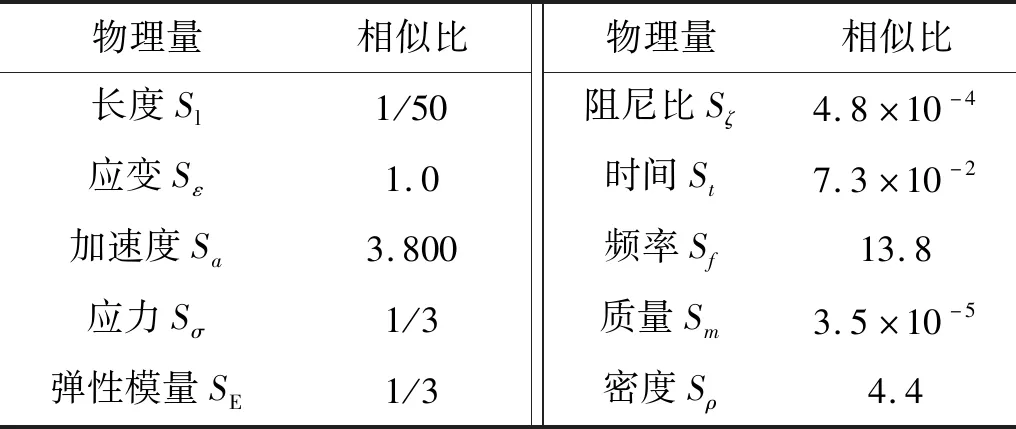
表1 模型相似比例Tab.1 The similitude proportionality coefficient of the model

簡化后的試驗模型上部結構高度為3.566 m。由于結構體形方正，各層的質心與剛性基本重合。下部結構為3×3的群樁基礎(見圖2)，圓樁樁徑0.08 m，樁長0.72 m，承臺板尺寸為0.92 m×0.92 m×0.1 m的立方體。模型上部結構的主要構件尺寸，如表2所示。模型材料選用與原型建筑材料力學性能相近的微粒混凝土、鍍鋅鐵絲和鐵絲網分別模擬原型建筑的混凝土、縱筋和樓板鋼筋網。模型的簡化過程及相似比例系數計算詳見文獻[6]。

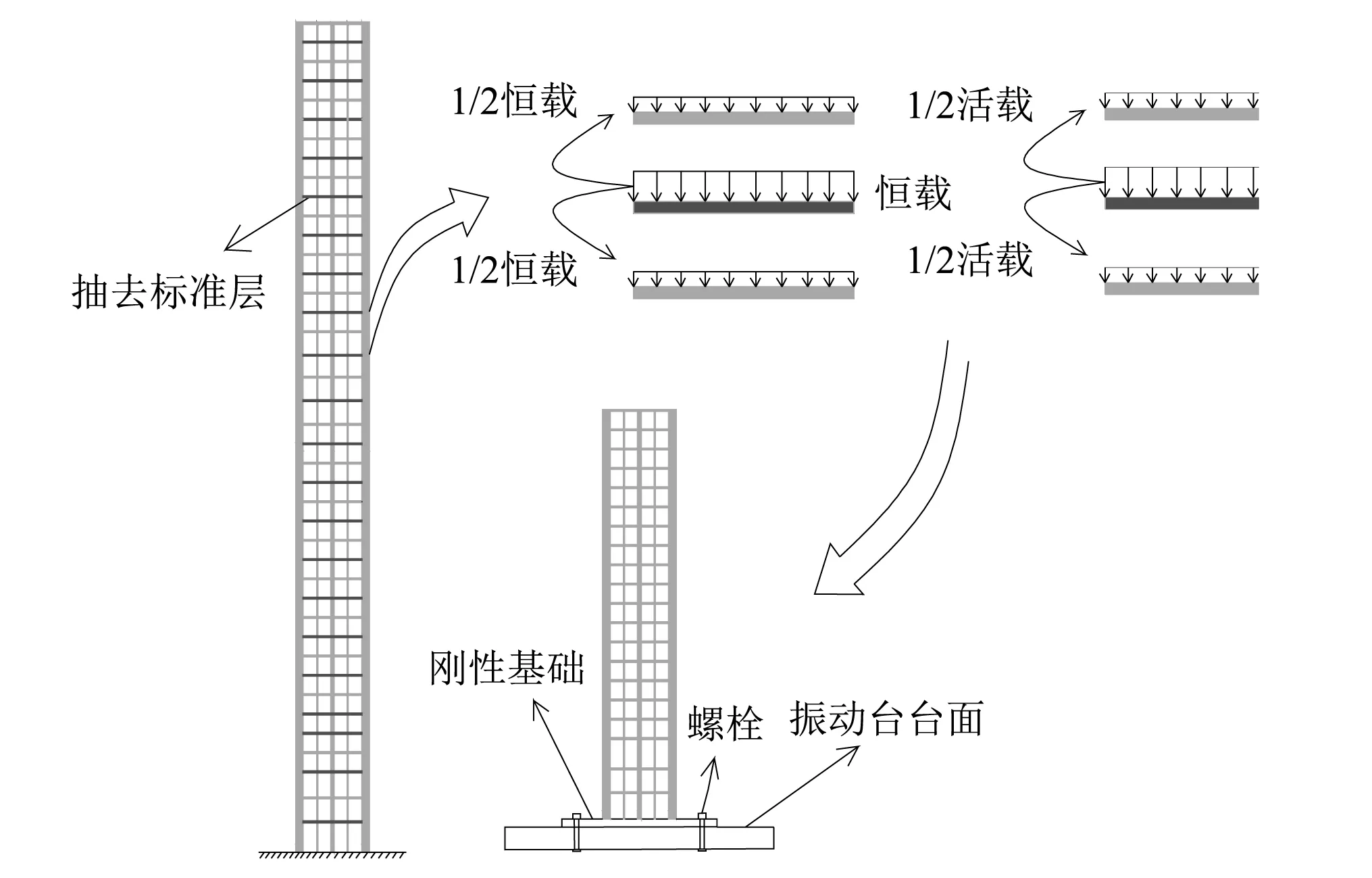
圖1 抽層過程Fig.1 The process of model simplifying

圖2 模型下部群樁基礎Fig.2 The view of the grouped piles foundation

試驗采用柔性圓筒狀土箱裝填試驗用土，相比剛性土箱和層狀剪切型土箱，柔性土箱能最大程度的降低“模型箱效應”[7]。該土箱直徑為3 m，土箱內試驗用土自下而上分別為砂土、砂質粉土和粉質黏土。土箱的構造和試驗用土的粒徑，如圖3和圖4所示。

為了保證上部結構的整體性，施工時核心筒采用塑料泡沫作為施工模板[8]，塑料泡沫對結構的力學性能影響極小且不用拆除。樓板和外框架采用木模板立模。最終的整體模型和樓層平面結構形式，如圖5和圖6所示。

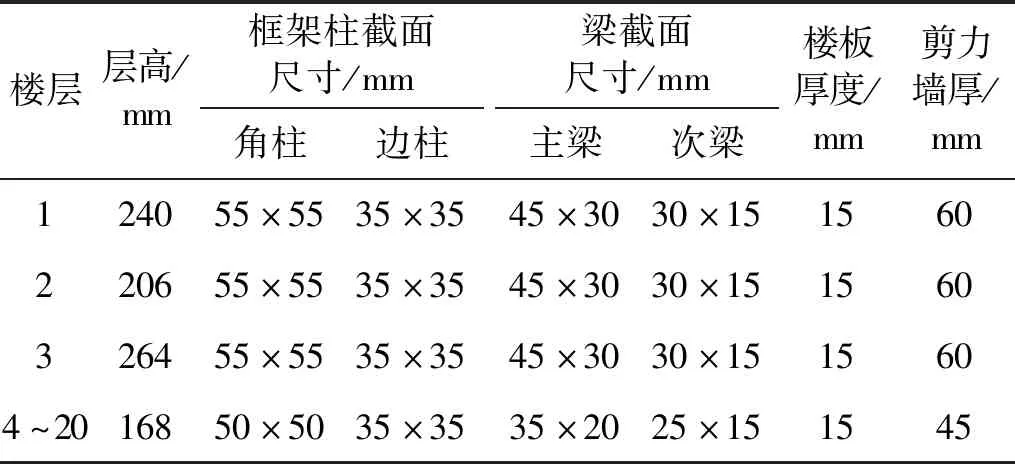
表2 模型上部結構的構件尺寸Tab.2 The component size of the superstructure

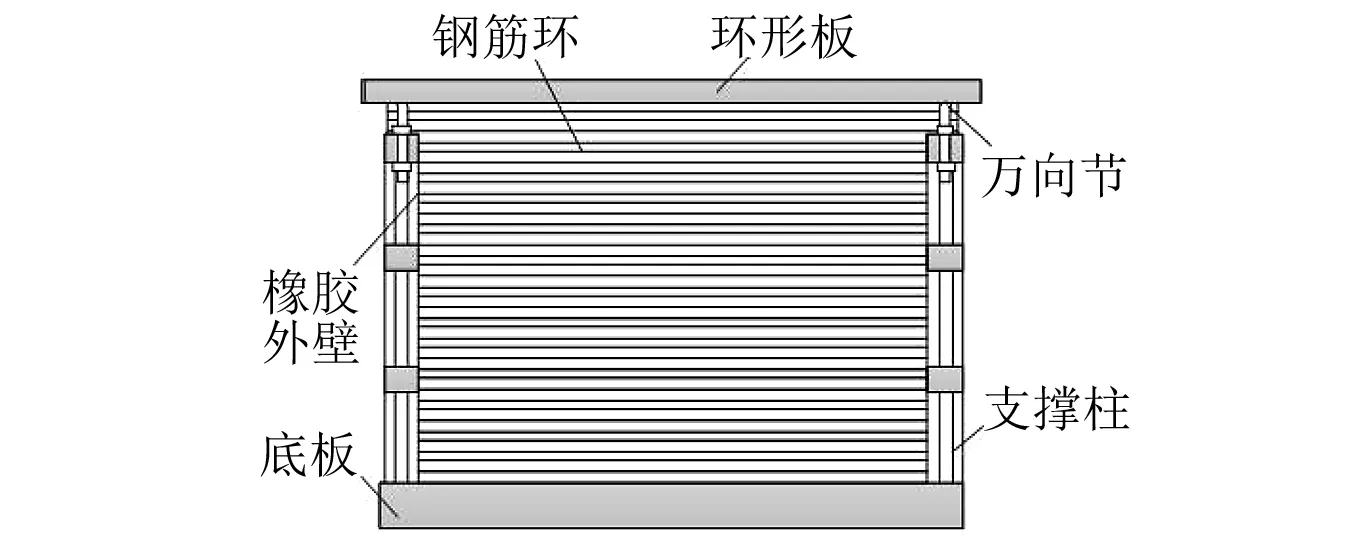
圖3 土箱結構示意圖Fig.3 The structure sketch of the soil box

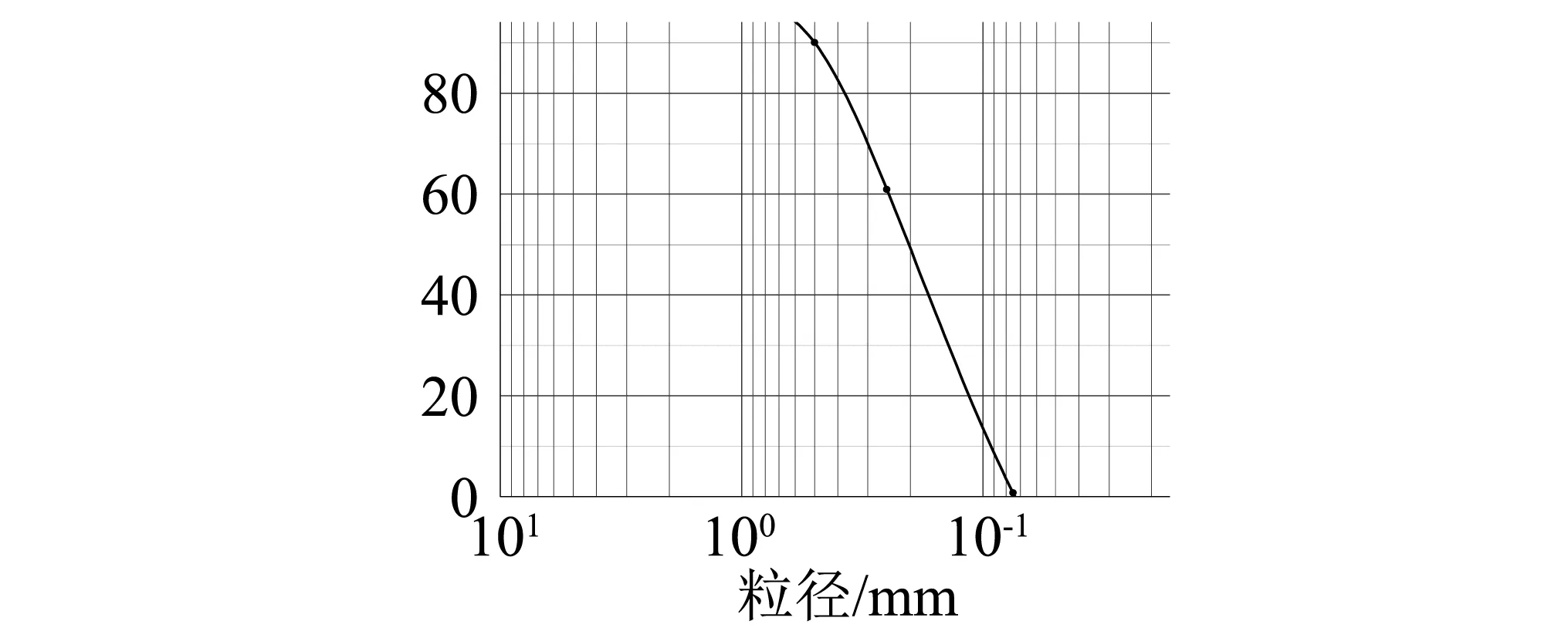
圖4 試驗用土粒徑曲線Fig.4 The particle size of soil

圖5 土—結構相互作用模型Fig.5 The soil-structure interaction model

圖6 樓層平面圖Fig.6 The plane graph of floor

1.2 模型簡化方法可靠性驗證

采用大型有限元軟件ANSYS建立了原型和簡化后的試驗模型，通過對比固有振型、固有周期，以及不同峰值加速度作用下的最大層間位移和最大層間位移角來判定簡化方法的可靠性。

通過對比兩個模型的振型圖(見圖7)可知，原型結構的低階振型與簡化模型一致。前兩階振型分別為沿Y軸和X軸方向的彎曲；第三階、第四階振型分別為沿Y軸和X軸方向的剪切變形，且均具有一個反彎點。將兩個模型的固有周期、最大層間位移和最大層間位移角進行對比，統計結果分別如表3～表5所示。固有周期最大誤差為2.6 %，層間位移的最大誤差為5.42 %，層間位移角的最大誤差為8.56 %。簡化模型的結構特性與原型結構較為接近，因此，該簡化方法是可行的，簡化后的試驗模型可以作為試驗的研究對象。

圖7 振型圖對比Fig.7 Comparison on the model shape

表3 固有周期的誤差Tab.3 The error of the natural period

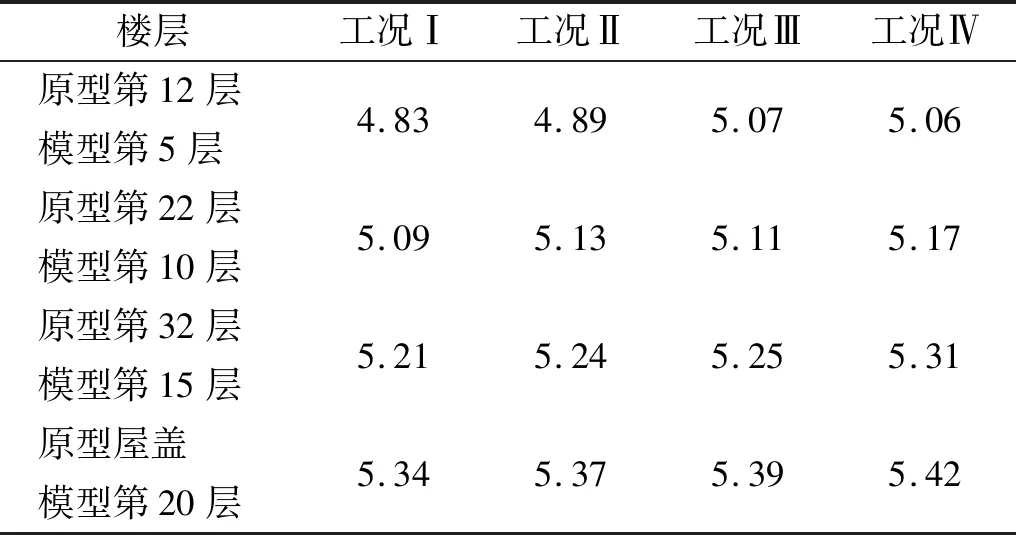
表4 層間位移的誤差Tab.4 The error of the story displacement %

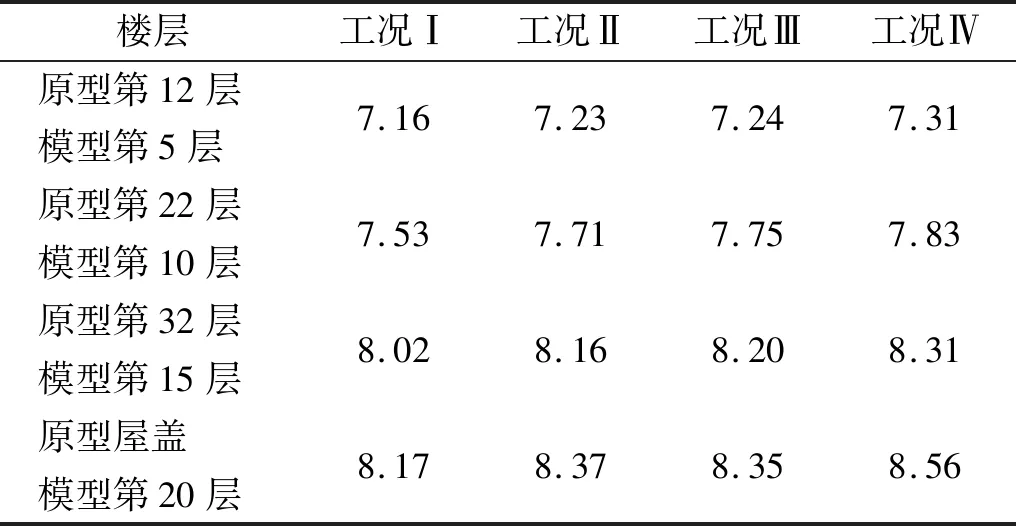
表5 層間位移角的誤差Tab.5 The error of the story drift %

1.3 測點布置

為獲得上部結構在多向地震作用下的動力反應，模型上部結構共布置了47個傳感器，其中加速度計27個，應變計12個，位移計8個。所有測點沿樓層高度均勻布置，測點布置如圖8所示。

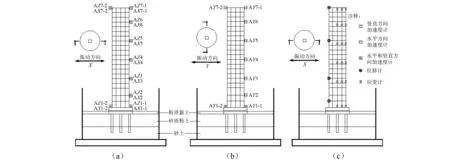
圖8 測點布置示意圖Fig.8 The sketch of the arrangement of gauges

1.4 振動臺性能與加載工況

振動臺的性能是影響試驗的成功與否的重要因素。本次試驗采用美國MTS公司引進的模擬地震振動臺，該振動臺采用電液伺服驅動方式，具備三向六自由度試驗能力，集臺面編程、迭代補償、數據分析和處理以及管理等功能于一體。最大承載重量25 t，最大驅動加速度為1.2g，能夠模擬簡諧振動、沖擊以及地震作用。該振動臺性能能夠滿足本試驗的需求。

試驗選用El Centro波、Kobe波和上海人工波三條天然地震波作為振動激勵。由試驗模型與原型結構的加速度相似比例Sa=3.8可得，在模擬七度和八度地震作用時，輸入振動臺的地震波峰值加速度應分別調整為0.38g和0.76g。試驗加載工況見表6所示。

1.5 破壞現象

試驗模型經歷了加速度峰值從0.38～0.76g不斷增大的過程，結構破壞現象簡述如下：

(1)七度罕遇水平地震作用后，FB模型無損傷發生，SSI模型上部結構中部的外框架角柱發生寬度約為1 mm的水平裂縫，核心筒和群樁基礎均未出現明顯裂縫。

(2)八度罕遇水平地震作用后，FB試驗模型的外框架柱底部發生寬度為1 mm的水平裂縫，核心筒無破壞現象；SSI試驗模型的群樁樁身出現約為1 mm的水平細微裂縫(見圖9)，上部結構中部的外框架柱水平裂縫未發生明顯擴大。

(3)九度罕遇水平地震作用后，FB試驗模型的外框架柱底部水平裂縫繼續延伸，同時，核心筒出現寬度約為1 mm的水平裂縫(見圖10)；SSI試驗模型的裂縫無擴大趨勢，受損情況與八度罕遇地震作用結果基本一致。

圖9 框架柱與核心筒的破壞Fig.9 The failure in frame column and core tube

圖10 樁基的破壞Fig.10 The failure in piles

2 結構固有特性

經過四次白噪聲掃頻，獲得了FB和SSI試驗模型在各工況下的振型、固有頻率和阻尼比。由于模型為對稱結構，X軸和Y軸方向的各階振型極為相似，因此本文僅對動力FB和SSI模型的X軸方向前兩階振型(見圖11)差別展開討論。X軸方向第一振型中，兩種模型的上部結構均成剪切型平擺。X軸方向第二振型中，FB模型的上部結構呈現帶有反彎點的平擺，而SSI模型仍保持剪切型平擺，說明考慮土對結構的影響后，上部結構的振動存在“振型滯后”現象。

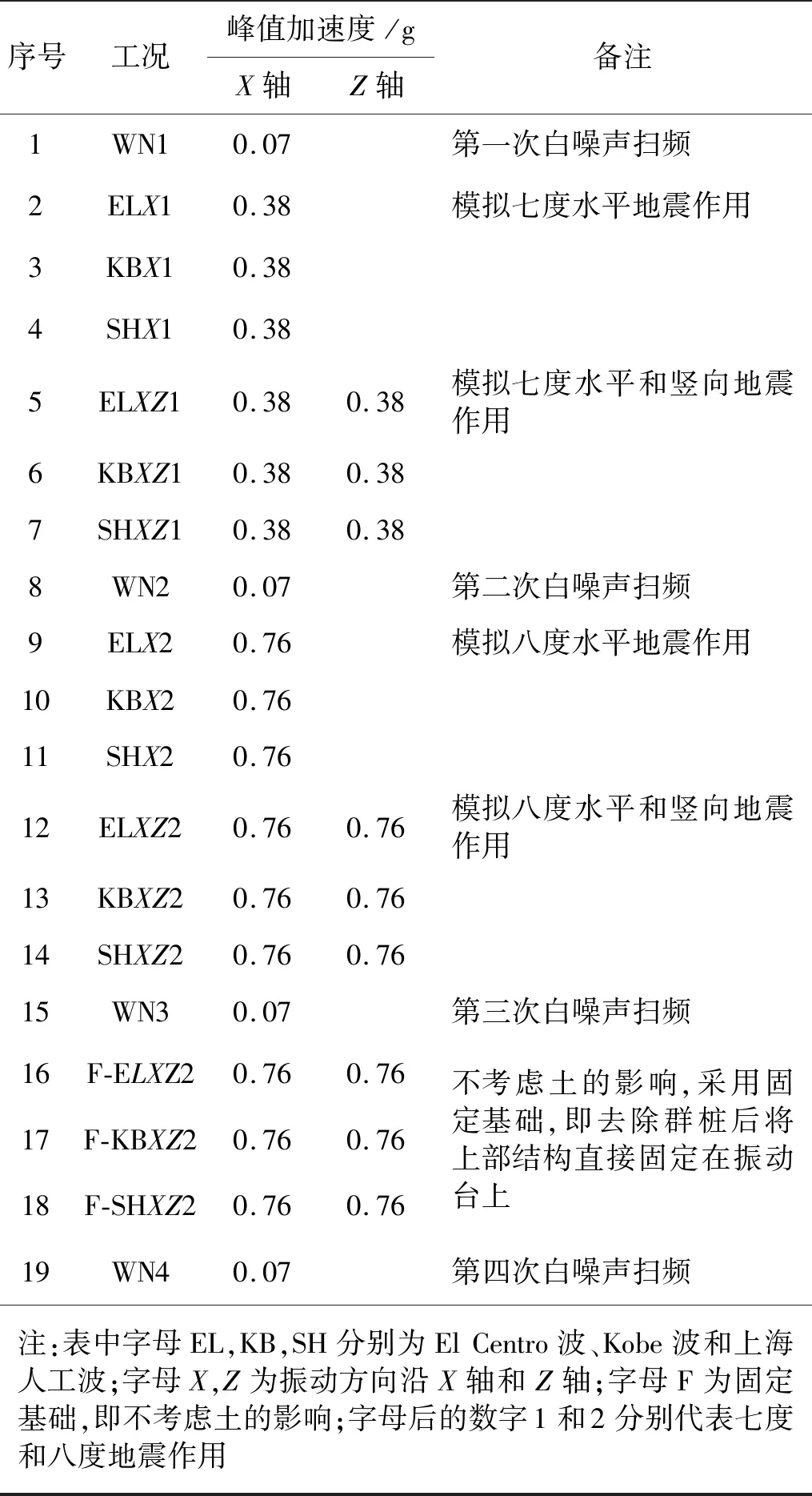
表6 加載工況Tab.6 Loading conditions

各工況下X軸方向第1振型的固有頻率、阻尼比如表7所示。隨著地震烈度的增大，固有頻率減小，阻尼比增大，表明結構的剛度不斷退化，破壞程度不斷增大。由于土能夠耗散更多的振動能量，使得SSI模型的阻尼比明顯大于FB模型，固有頻率小于FB模型。

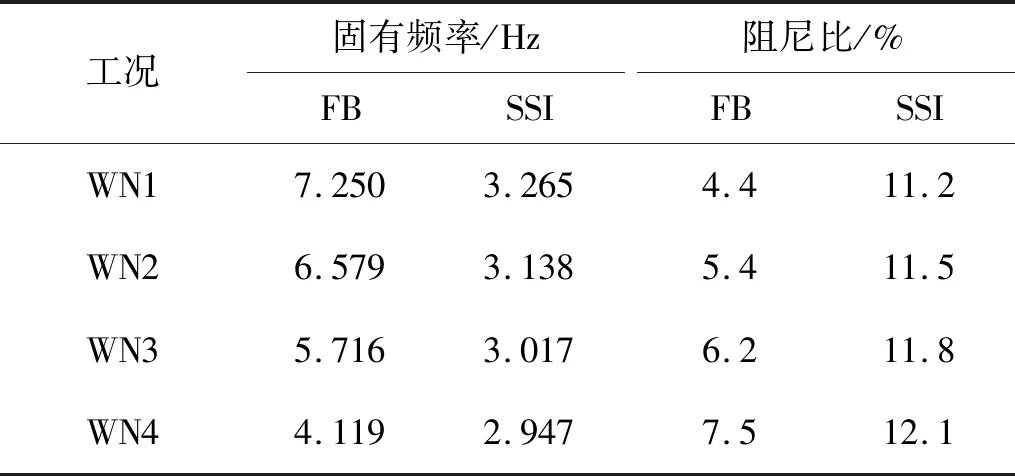
表7 X軸方向第1振型固有頻率和阻尼比Tab.7 The natural frequency and damping ratio of the 1st mode in X-direction

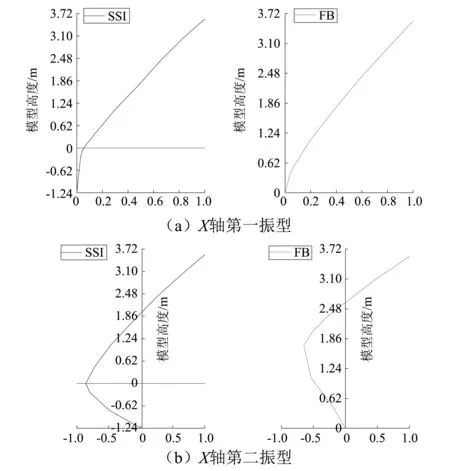
圖11 動力相互作用模型與固定基礎型振型對比Fig.11 Comparison on the mode shapes of SSI and FB

3 水平方向地震反應

3.1 水平方向加速度反應

圖12給出了SSI試驗模型在三種地震波作用下上部結構沿X軸方向的最大相對加速包絡圖。定義上部結構的最大相對加速度為各樓層峰值加速度相對于第一層樓板峰值加速度的最大值。在單向水平或多向地震作用下，各樓層沿X軸方向的峰值加速度均隨地震烈度的增大而增大。當地震烈度相同時，多向地震作用下各樓層沿X軸方向的最大相對加速度均大于單向地震作用的結果。在多向耦合地震作用下，各樓層沿X軸方向的最大相對加速度均遠大于同烈度的單向水平地震作用的結果。上述現象表明，相比于單向水平地震作用，多向地震對作用平面內的水平方向加速度具有放大效應。

圖13給出了SSI試驗模型在三種地震波作用下上部結構各層沿Y軸方向的最大相對加速包絡圖。在單向水平或多向地震作用下，各樓層沿Y軸方向的最大相對加速度均隨地震烈度的增大而增大。當地震烈度相同時，單向水平地震作用下各樓層沿Y軸方向的最大相對加速度均小于多向地震作用的結果。上述現象表明，相比于單向水平地震作用，多向地震對作用平面外的水平方向加速度也具有放大效應，但加速度增量小于平面內加速度一個數量級。

3.2 層間位移和層間位移角

定義最大層間位移角為結構各層沿某一水平軸線方向的最大層間位移與各層層高之比。模型沿X軸方向的最大層間位移和層間位移角計算結果，如表8所示。當地震烈度相同時，多向地震作用下X軸方向的最大層間位移和層間位移角均大于單向水平地震作用結果，這是多向地震對平面內的水平方向加速度具有放大效應的結果。

圖12 SSI試驗模型上部結構X軸方向最大相對加速度包絡圖Fig.12 The envelope graph of the maximum horizontal acceleration in the X-direction of the SSI test model

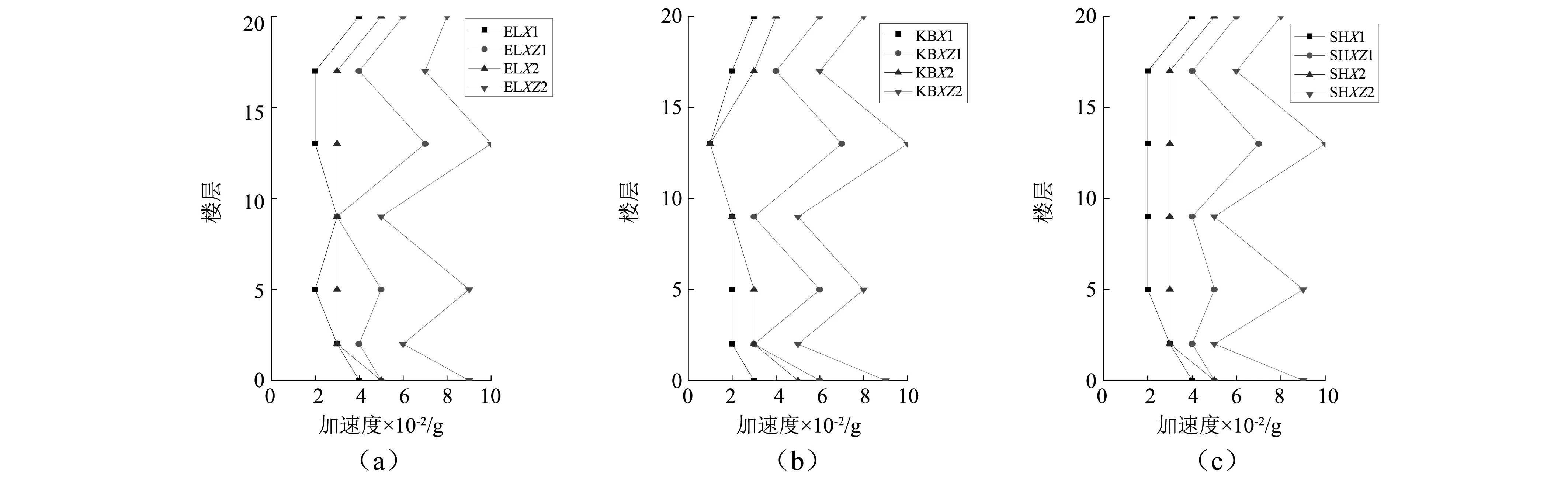
圖13 SSI試驗模型上部結構Y軸方向最大相對加速度包絡圖Fig.13 The envelope graph of the maximum horizontal acceleration in the Y-direction of the SSI test model

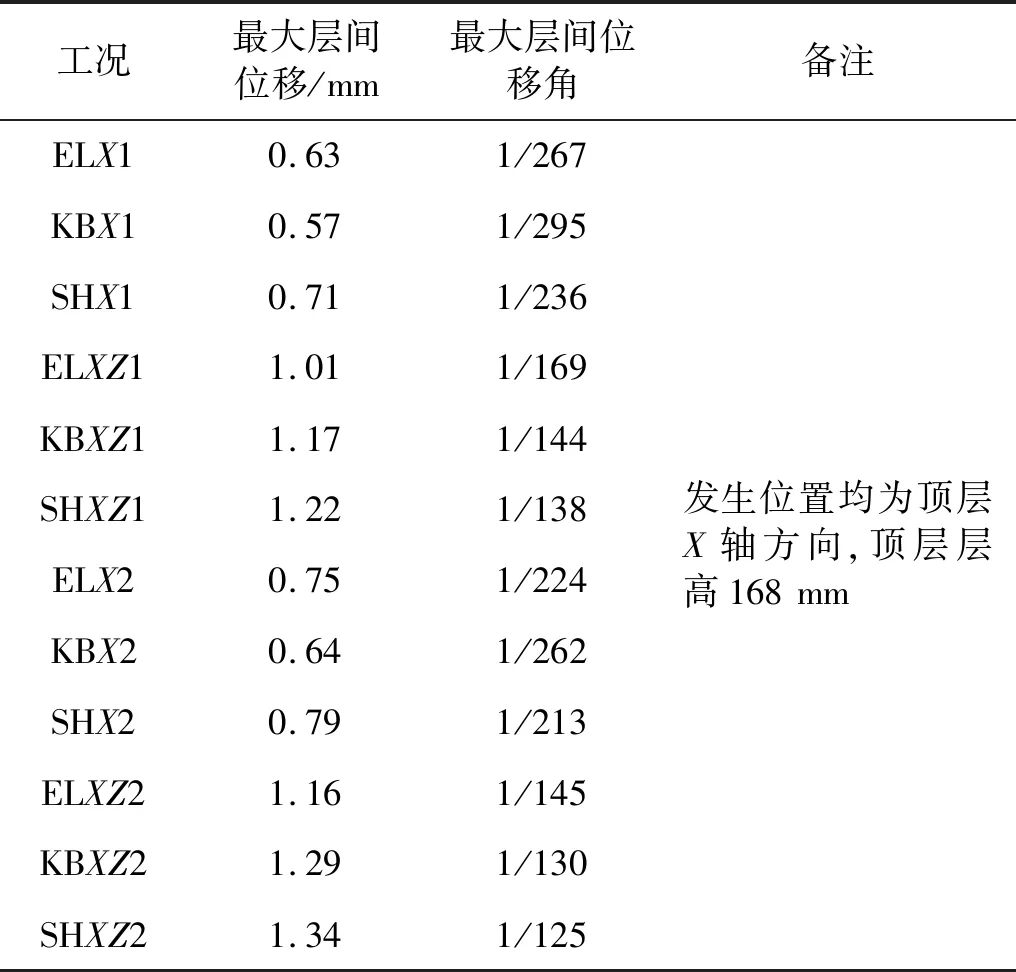
表8 X軸方向最大層間位移和層間位移角Tab.8 The maximum story displacement and story drift at the X-direction

3.3 水平方向動應變反應

框架—核心筒結構底部的動應變能夠反映結構傾覆破壞的趨勢[9]。由于兩種地震波作用下水平方向的最大拉壓應變變化趨勢相同，因此，本文僅對El Centro波作用下SSI試驗模型上部結構底部的核心筒角部和外框架角柱最大拉壓應變進行討論，如圖14所示。

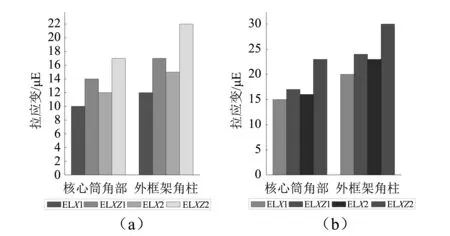
圖14 SSI試驗模型上部結構底部的最大拉壓應變Fig.14 The maximum tensile and compression strain at the bottom of superstructure of the SSI test model

由圖14可知，同等烈度地震作用下，多向地震所產生的水平方向最大拉壓應變均大于水平單向地震作用的結果。隨著地震烈度的增大，結構底部水平方向的最大拉壓應變也隨之增大。各加載工況作用下，外框架角柱的最大拉壓應變均大于核心筒角部的結果。由此可知，相比水平單向地震作用，在多向地震作用下，結構底部水平方向的拉壓應變更大，外框架角柱更易發生拉壓破壞，結構發生傾覆破壞的概率也更大。

4 豎向地震反應

4.1 豎向加速度反應

樓層豎向加速度的大小能夠表征上部結構受到豎向慣性力的大小，慣性力越大，豎向主要承重構件就越易發生軸壓破壞[10-12]。圖15給出了多向地震作用下各樓層豎向最大相對加速度。

由圖15可知，在地震烈度為七度的三種多向地震波作用下，樓層豎向最大相對加速度均小于八度地震多向地震作用的結果，即在多向地震作用下，各樓層的豎向最大相對加速度隨地震烈度的增大而增大。當地震烈度相同時，SSI模型上部結構的豎向最大相對加速度隨樓層的增大并無明顯差別，而FB模型上部結構的豎向最大相對加速度隨樓層的增大而增大。上述現象表明，SSI模型通過土對振動能量的耗散，能夠降低上部結構的豎向加速度。

4.2 豎向層間位移

采用MATLAB軟件將各測點的豎向加速度記錄經傅里葉變換由時域轉換為頻域，進而在頻域中進行二次積分，積分結果再經傅里葉逆變換即可得到樓層各測點的豎向位移時程。不同工況下模型的最大豎向層間位移，如表9所示。

在9種不同工況下，豎向最大層間位移均發生在模型頂層。兩種模型上部結構的豎向層間位移均隨地震烈度的增大而增大。烈度相同的同種多向地震波作用下，FB模型的豎向最大層間位移是SSI模型的1.7倍，表明在多向地震作用下，FB模型的豎向最大層間位移遠大于SSI模型。

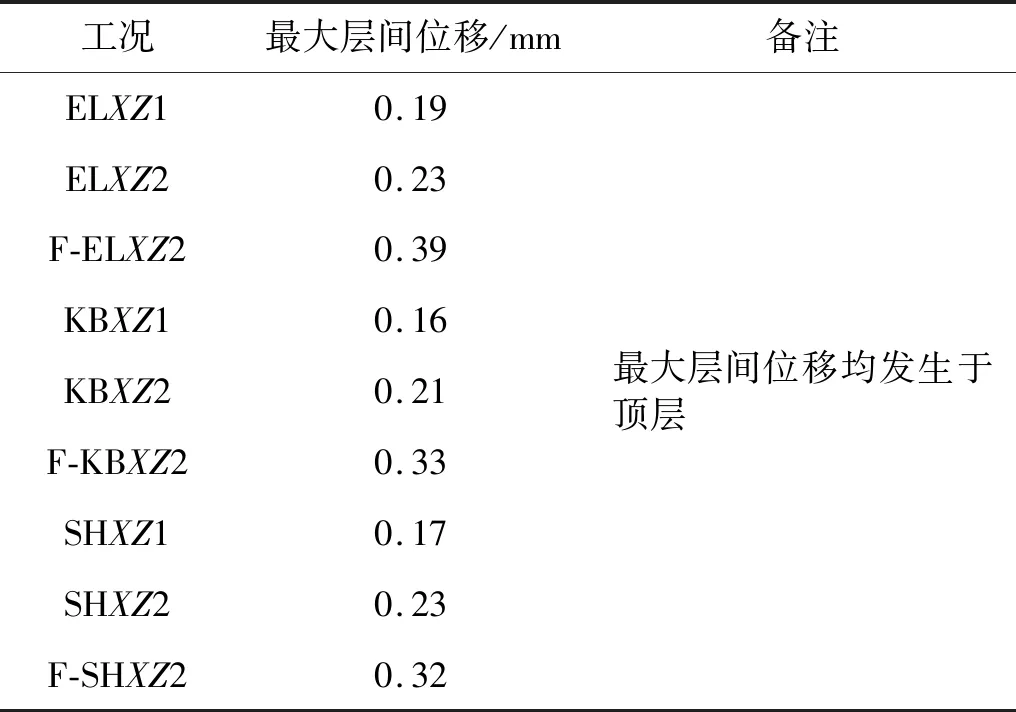
表9 豎向最大層間位移Tab.9 The maximum story displacement at the vertical direction

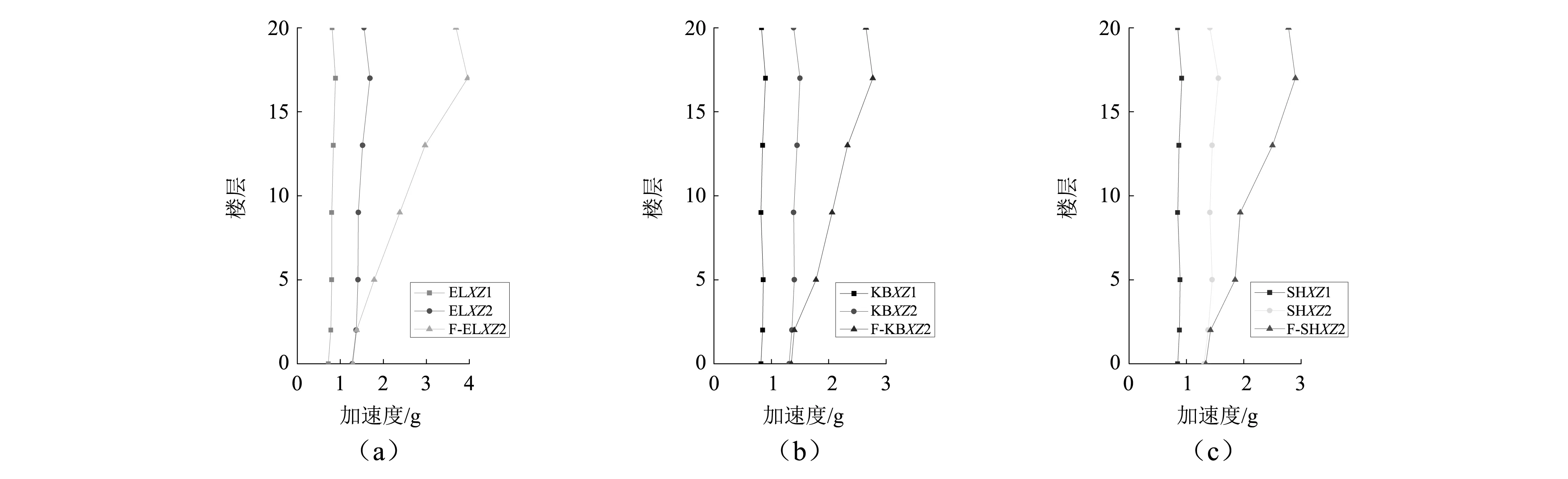
圖15 試驗模型上部結構豎直方向最大加速度包絡圖Fig.15 The envelope graph of the maximum vertical acceleration of the test models

5 數值模擬

采用有限元軟件(ANSYS)對SSI和FB兩個試驗模型進行數值模擬，通過對比兩種模型的數值分析結果驗證振動臺試驗結果的合理性。采用ANSYS單元庫中的梁單元Beam 188模擬上部結構的梁和柱，核心筒和樓板采用殼單元Shell 181，樁、承臺和土體采用實體單元Solid 45模擬，土和承臺、樁的接觸面采用接觸單元模擬。FB數值模型的底部結點采用固定約束，SSI數值模型的土體四周采用彈性約束，土體底部采用固定約束。FB和SSI數值模型如圖16所示。

經振型計算，FB和SSI數值模型的振型與試驗模型的振型完全相符。兩種數值模型在X軸方向前兩階振型，如圖17所示。經模態計算，FB和SSI數值模型在X軸方向第1振型的固有頻率分別為12.032 Hz和9.171 Hz，阻尼比分別為5.5 %和13.4 %，即FB模型的固有頻率大于SSI模型，阻尼比小于SSI模型，數值模擬計算結果與試驗結果相符。

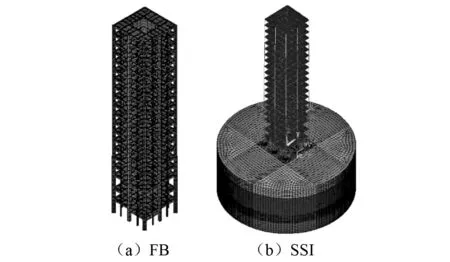
圖16 FB和SSI數值模型Fig.16 The numerical models of FB and SSI

采用El Centro波進行各種工況的地震時程分析[13-15]。SSI數值模型的X和Y軸方向最大相對加速度計算結果，如圖18所示。不同工況下SSI數值模型沿X軸方向的最大層間位移和層間位移角計算結果，如表10所示。在單向水平和多向El Centro波作用下，SSI數值模型上部結構底部的最大拉壓應變計算結果，如圖19所示。FB和SSI在八度多向El Centro波作用下的各樓層豎向加速度計算結果，如圖20所示。豎向最大層間位移分別為0.20 mm和0.34 mm。上述兩種數值模型的動力反應量計算結果，以及各反應量的變化趨勢均與試驗結果相一致，從而驗證了研究成果的可靠性。

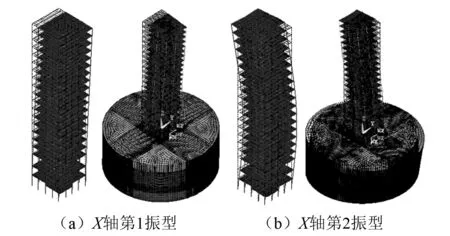
圖17 振型計算結果Fig.17 The calculation result of mode shapes

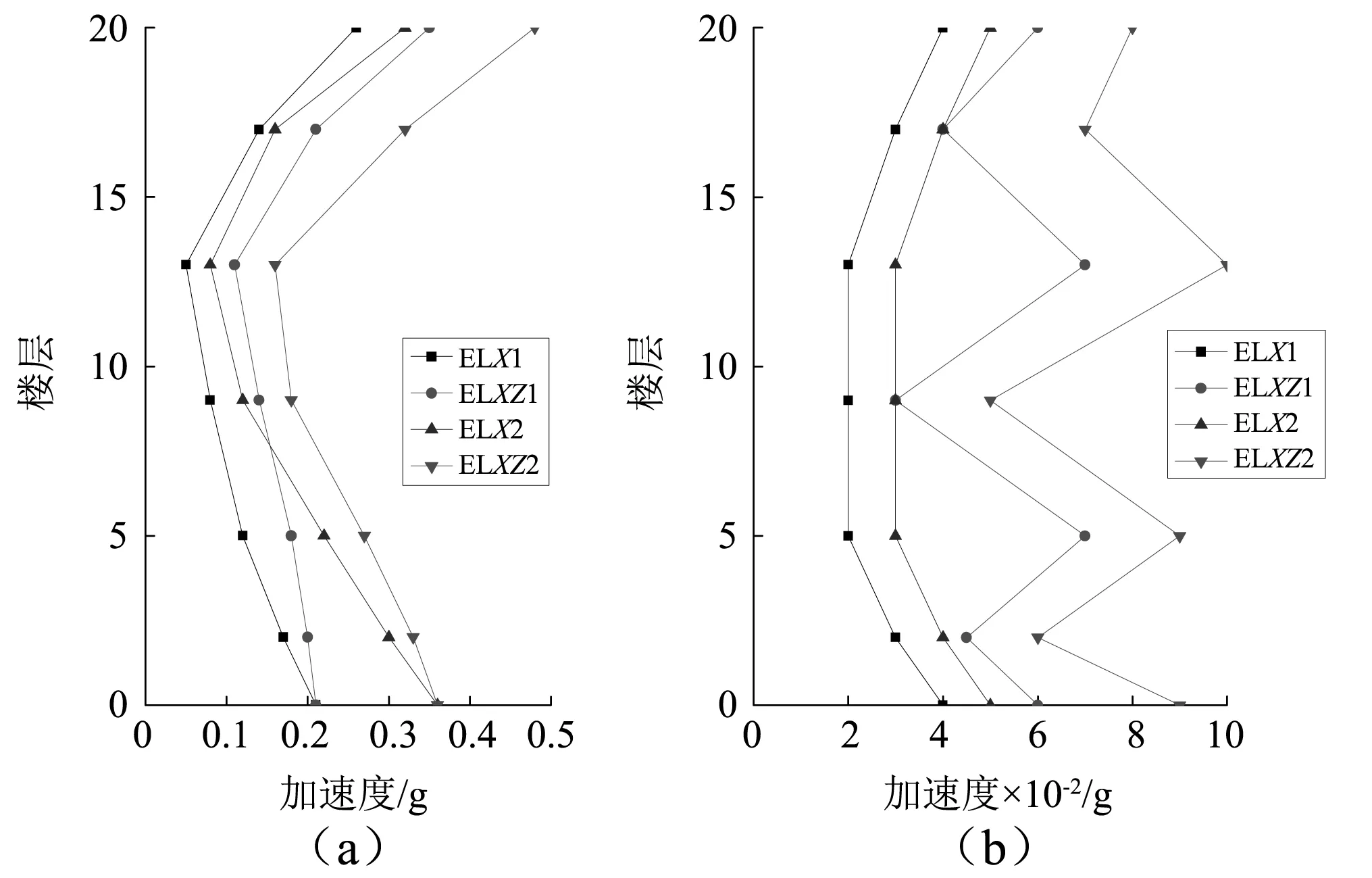
圖18 SSI數值模型上部結構X和Y軸方向最大相對加速度包絡圖Fig.18 The envelope graph of the maximum horizontal acceleration in the X- and Y-direction of the SSI numerical model

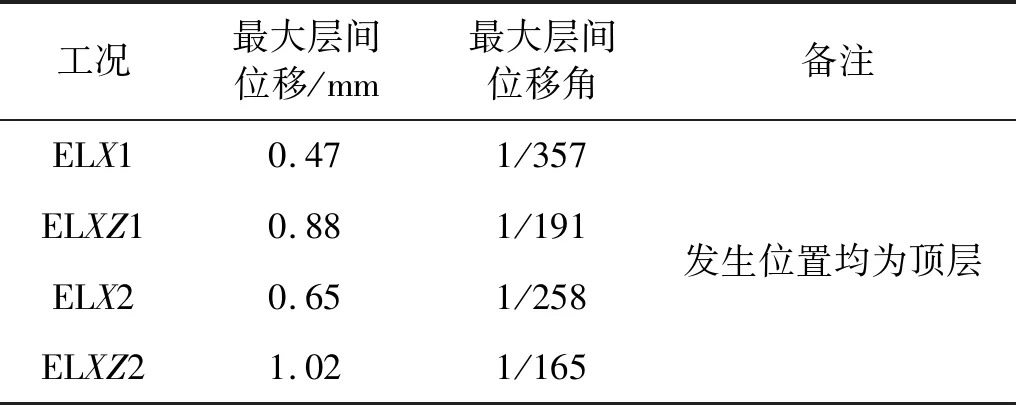
表10 SSI數值模型X軸方向最大層間位移和層間位移角Tab.10 The maximum story displacement and story drift of the SSI numerical model in the X direction

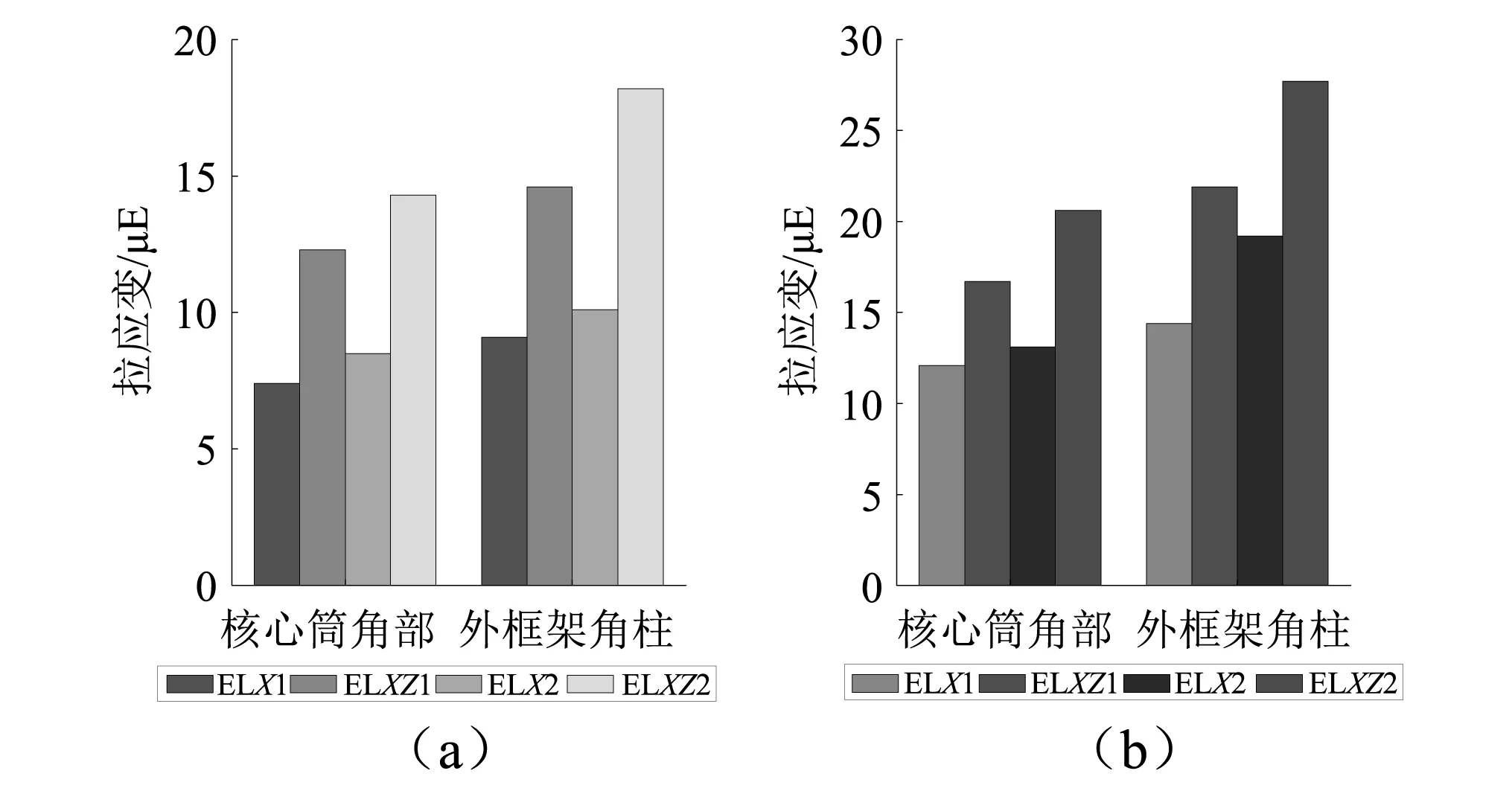
圖19 SSI數值模型上部結構底部最大拉壓應變Fig.19 The maximum tensile and compression strain at the bottom of superstructure of the SSI numerical model

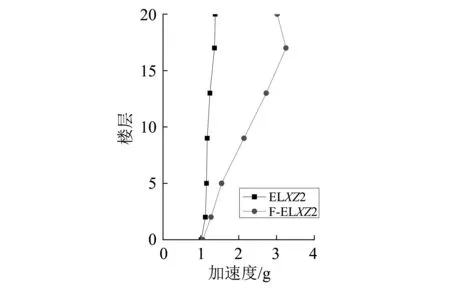
圖20 數值模型上部結構豎直方向最大加速度包絡圖Fig.20 The envelope graph of the maximum vertical acceleration of the numerical models

6 結 論

本文研究了框架—核心筒結構在多向地震作用下的動力性能，通過振動臺試驗獲得了SSI模型在不同工況下，上部結構沿水平和豎向的樓層峰值加速度、最大層間位移、大層間位移角以及動應變，經對比分析得到以下結論：

(1)SSI模型通過土對地震能量的耗散，使得體系的固有頻率小于FB模型。相比于FB模型，SSI模型上部結構的低階振型存在“振型滯后”現象。

(2)相比于單向水平地震作用，多向地震對SSI模型上部結構水平方向的加速度、層間位移、層間位移角，以及框架—核心筒底部的動應變均具有放大效應。

(3)相比于FB模型，SSI模型通過土對地震能量的耗散，使得上部結構豎向的加速度和層間位移均小于FB模型。

(4)在對框架—核心筒高層建筑進行結構時，建議增加SSI模型的多向地震作用動力響應計算。