帶緣板阻尼結(jié)構(gòu)轉(zhuǎn)子葉片振動(dòng)特性的影響參數(shù)分析

張大義，楊 誠(chéng)，夏 穎，付檢偉，洪 杰

(1.北京航空航天大學(xué) 能源與動(dòng)力工程學(xué)院，北京 100191;2.先進(jìn)航空發(fā)動(dòng)機(jī)協(xié)同創(chuàng)新中心，北京 100191)

在現(xiàn)代航空燃?xì)鉁u輪發(fā)動(dòng)機(jī)中，因振動(dòng)帶來(lái)的葉片高周疲勞斷裂問(wèn)題是影響發(fā)動(dòng)機(jī)可靠性的關(guān)鍵問(wèn)題之一[1]。對(duì)于葉片的振動(dòng)抑制而言，干摩擦阻尼結(jié)構(gòu)由于其減振效果明顯、結(jié)構(gòu)簡(jiǎn)單及可靠性高等特點(diǎn)，在航空發(fā)動(dòng)機(jī)中得以廣泛應(yīng)用。常見(jiàn)干摩擦阻尼結(jié)構(gòu)形式包括凸肩、葉冠和緣板阻尼結(jié)構(gòu)等[2-3]。其中，緣板阻尼結(jié)構(gòu)(Under Platform Damper,UPD)因附加離心負(fù)荷小、對(duì)氣動(dòng)性能無(wú)不利影響等優(yōu)點(diǎn)，被廣泛應(yīng)用于風(fēng)扇葉片和渦輪葉片的減振設(shè)計(jì)[4]，如CFM56-3、太行等發(fā)動(dòng)機(jī)的風(fēng)扇葉片，以及JT9D、CF6、RB211、BR715、АЛ-31Ф、РД33等發(fā)動(dòng)機(jī)的高壓渦輪葉片[5-6]。

在微觀尺度對(duì)緣板與阻尼塊接觸表面的力學(xué)特性進(jìn)行定量表征是研究緣板阻尼結(jié)構(gòu)的首要工作。早期研究多采用宏觀滑移模型，其假設(shè)接觸面上的變形和壓力都是均勻分布的，接觸面整體同時(shí)進(jìn)入黏滯或滑移狀態(tài)。代表性工作包括：Yang等[7-8]提出的耦合雙接觸面模型，Sanliturk等[9]建立的小自由度理論模型，郝燕平等[10-11]采用的B-G簡(jiǎn)化模型。與宏觀滑移模型相比，微動(dòng)滑移模型則可以更好地刻畫接觸表面之間存在的局部滑移現(xiàn)象，進(jìn)而更準(zhǔn)確地預(yù)測(cè)接觸面力學(xué)特性[12-13]。代表性工作如Sanliturk等[14]采用多個(gè)接觸對(duì)并聯(lián)形式建立微動(dòng)滑移模型，漆文凱等[15]采用整體局部一體化模型分析緣板阻尼結(jié)構(gòu)，Panning等[16]采用微動(dòng)滑移模型對(duì)比分析楔形緣板阻尼結(jié)構(gòu)與圓柱形緣板阻尼結(jié)構(gòu)的減振效果。Petrov[17]采用自行開(kāi)發(fā)的干摩擦非線性振動(dòng)響應(yīng)求解程序，分析得到了不同結(jié)構(gòu)形式阻尼結(jié)構(gòu)的減振效果。

在宏觀尺度研究葉片振動(dòng)特性的關(guān)鍵影響參數(shù)及影響規(guī)律是工程應(yīng)用中的關(guān)注點(diǎn)，大量文獻(xiàn)基于宏觀滑移模型開(kāi)展了相關(guān)研究，如：郝燕平等[18]采用動(dòng)柔度法計(jì)算分析了緣板阻尼器切向剛度和摩擦面的摩擦因數(shù)對(duì)葉片響應(yīng)的影響，吳向宇等[19]采用軌跡跟蹤法計(jì)算分析了阻尼塊質(zhì)量的影響規(guī)律，李琳等[20]采用B-G集中參數(shù)模型分析了緣板阻尼結(jié)構(gòu)對(duì)寬頻多階次激勵(lì)的減振效果。上述研究均采用宏觀滑移模型，因此無(wú)法考慮緣板-阻尼塊復(fù)雜接觸狀態(tài)的影響，進(jìn)而限制了所獲得規(guī)律的準(zhǔn)確性。

借鑒上述工作，作者在文獻(xiàn)[21]中針對(duì)緣板阻尼結(jié)構(gòu)建立了分布式摩擦力學(xué)模型，并建立了帶有分布式摩擦高維度葉片的振動(dòng)響應(yīng)求解方法。本文在其基礎(chǔ)上，將微動(dòng)滑移模型應(yīng)用于高維度葉片模型的振動(dòng)特性分析，進(jìn)一步研究正壓力、質(zhì)量、摩擦因數(shù)等緣板阻尼結(jié)構(gòu)關(guān)鍵參數(shù)對(duì)葉片振動(dòng)特性的影響規(guī)律，為工程設(shè)計(jì)提供亟需的數(shù)據(jù)參考。

1 理論模型與求解方法

緣板阻尼結(jié)構(gòu)簡(jiǎn)圖及工作原理如圖1所示。在工作狀態(tài)，緣板阻尼塊由于離心載荷作用，壓緊在兩個(gè)相鄰葉片緣板下表面。當(dāng)葉片發(fā)生振動(dòng)時(shí)，緣板與阻尼塊之間發(fā)生相對(duì)運(yùn)動(dòng)，接觸面干摩擦效應(yīng)消耗葉片振動(dòng)的部分能量。

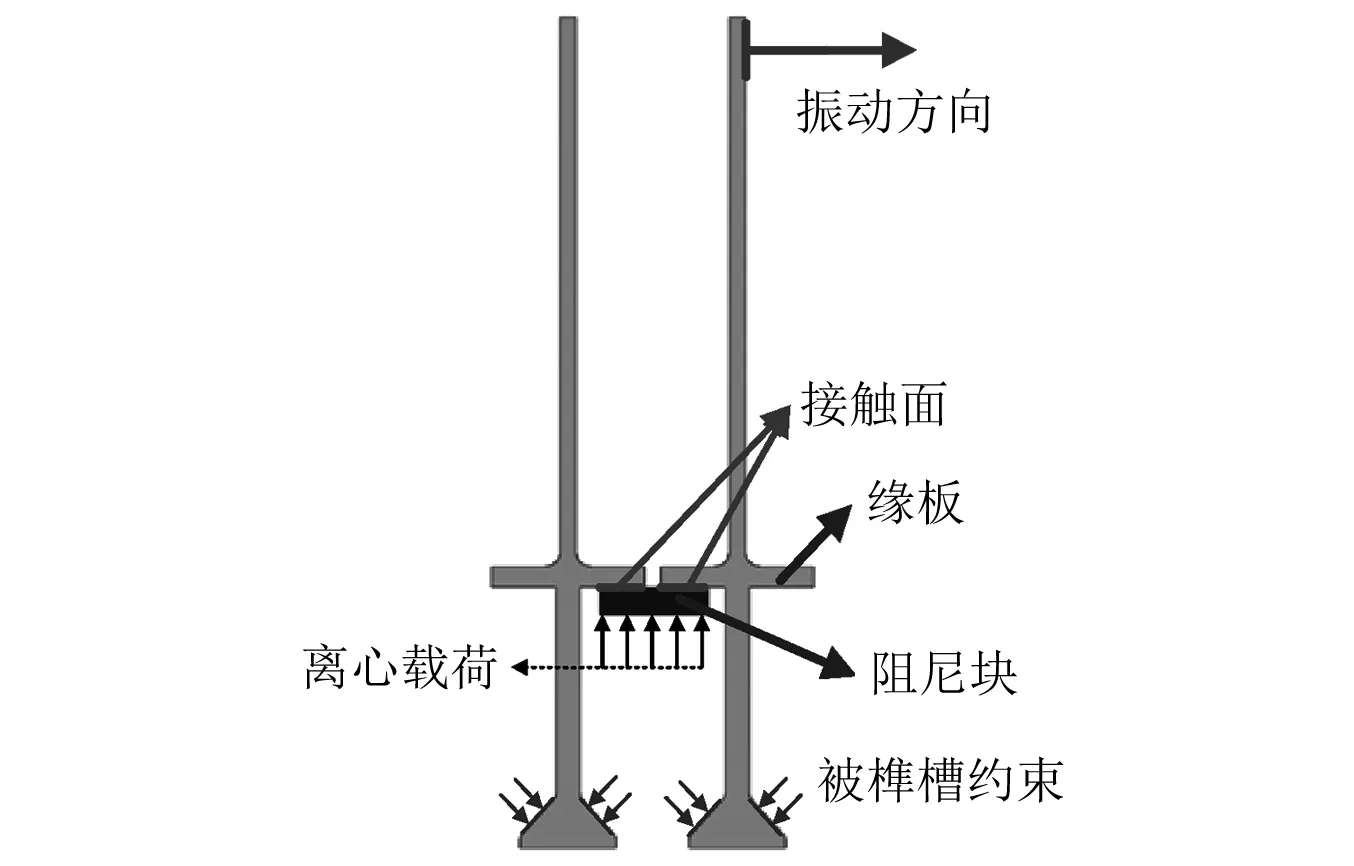
圖1 緣板阻尼結(jié)構(gòu)原理圖Fig.1 The sketch of UPD

1.1 微分形式摩擦力

遲滯摩擦模型被廣泛用于確定接觸點(diǎn)對(duì)的切向摩擦力。當(dāng)正壓力不變時(shí)，接觸點(diǎn)對(duì)的沿接觸面切向摩擦力的表達(dá)式為[22]

(1)

式中：f為摩擦力；kt為切向接觸剛度；μ為摩擦因數(shù)；N為接觸面的法向壓力；gt為接觸點(diǎn)對(duì)沿接觸面切向方向的相對(duì)位移；sgn(·)為符號(hào)函數(shù)，表征摩擦力始終與相對(duì)運(yùn)動(dòng)的方向相反。

大多文獻(xiàn)中采用式(1)所示的積分形式的摩擦力學(xué)模型。其局限性在于式(1)僅適用于正壓力不變的情況；當(dāng)正壓力變化時(shí)，需要在每一個(gè)時(shí)間步內(nèi)，通過(guò)復(fù)雜計(jì)算來(lái)判斷接觸面的接觸狀態(tài)(黏滯，分離或滑移)。本文計(jì)算分析中采用微分形式摩擦力，摩擦力對(duì)時(shí)間的導(dǎo)數(shù)為

(2)

式中：H(·)為Heaviside函數(shù)，滿足

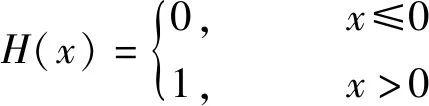
(3)

將摩擦力寫成如式(2)所示，可以將摩擦力視為附加的自由度直接參與到動(dòng)力方程的求解中，而不必考慮摩擦力對(duì)原有動(dòng)力學(xué)方程復(fù)雜的約束條件，簡(jiǎn)化了摩擦力的求解過(guò)程。微分形式的摩擦力學(xué)模型對(duì)于宏觀滑移模型和微觀滑移模型均適用。

1.2 非線性摩擦力的等效剛度和等效阻尼

阻尼塊與葉片緣板接觸表面的非線性摩擦力會(huì)改變?nèi)~片的剛度和阻尼，進(jìn)而導(dǎo)致其動(dòng)力學(xué)特性如共振頻率、振動(dòng)幅值等發(fā)生變化。將非線性摩擦力近似表達(dá)為如式(4)所示的位移和速度的線性組合

(4)

在不同時(shí)刻式(4)的左端項(xiàng)和右端項(xiàng)的相對(duì)誤差是不同的。當(dāng)Kad和Cad選取合適的值時(shí)，可以保證在一個(gè)振動(dòng)周期內(nèi)，此近似關(guān)系的相對(duì)誤差最小。采用最小二乘法得到近似關(guān)系式(5)的誤差函數(shù)為

(5)

根據(jù)誤差函數(shù)取極小值推導(dǎo)可得非線性摩擦力的等效剛度和等效阻尼，如式(6)～式(7)所示。

(6)

(7)

等效剛度和等效阻尼可以近似地定量反映出接觸面摩擦力對(duì)葉片剛度和阻尼帶來(lái)的改變，一定程度上決定了其對(duì)葉片動(dòng)力學(xué)特性的影響，其中，等效剛度主要影響葉片共振頻率，而等效阻尼主要影響葉片在各種不同激勵(lì)條件下的響應(yīng)幅值。上述公式給出的等效剛度和等效阻尼的表達(dá)式，對(duì)于宏觀滑移模型和微觀滑移模型均適用。

1.3 分布式接觸摩擦模型

微分形式的分布式接觸摩擦模型是Zhang等提出的一種微動(dòng)滑移模型，如圖2所示。通過(guò)多對(duì)接觸點(diǎn)對(duì)的形式，可以考慮接觸面上部分接觸點(diǎn)發(fā)生滑移，而其他接觸點(diǎn)保持黏滯狀態(tài)的情況。

圖2 分布式接觸摩擦模型示意圖Fig.2 A sketch of distributed contact model

實(shí)際工作時(shí)，接觸面的法向壓力分布是不均勻的。當(dāng)接觸的特征時(shí)間遠(yuǎn)大于彈性波在接觸面上的傳播時(shí)間時(shí)，該系統(tǒng)在運(yùn)動(dòng)過(guò)程的每一個(gè)時(shí)刻都處在平衡狀態(tài)。由此，將慣性力視作外力采用靜力學(xué)計(jì)算得到的接觸面壓力分布與接觸面發(fā)生相對(duì)運(yùn)動(dòng)時(shí)的壓力分布是相同的，該條件稱為接觸應(yīng)力的準(zhǔn)靜態(tài)條件。根據(jù)Zhang等的推導(dǎo)結(jié)論，緣板阻尼結(jié)構(gòu)滿足準(zhǔn)靜態(tài)條件。因此，通過(guò)靜力學(xué)計(jì)算來(lái)確定緣板阻尼結(jié)構(gòu)接觸面的壓力分布形式。

緣板阻尼器可以根據(jù)圖2等效為帶分布式接觸面的單自由度振子模型。則根據(jù)式(2)，計(jì)算緣板阻尼器運(yùn)動(dòng)的方程為

(8)

式中:x為阻尼塊沿接觸面切向的位移；m為阻尼塊的質(zhì)量；yi為葉片緣板上第i個(gè)接觸點(diǎn)的位移;fi和Ni分別為接觸面上第i個(gè)接觸點(diǎn)上的摩擦力和正壓力；kit表示第i個(gè)接觸點(diǎn)的切向接觸剛度。假設(shè)緣板各節(jié)點(diǎn)的運(yùn)動(dòng)狀態(tài)已知，根據(jù)靜力學(xué)求得的壓力Ni，通過(guò)對(duì)式(8)進(jìn)行數(shù)值積分即可求解緣板阻尼結(jié)構(gòu)接觸面的分布式摩擦力fi。

2 關(guān)鍵參數(shù)對(duì)等效剛度與等效阻尼的影響

如前所述，緣板-阻尼塊接觸面之間的摩擦力會(huì)改變?nèi)~片的剛度和阻尼，進(jìn)而影響其動(dòng)力學(xué)特性。通過(guò)對(duì)摩擦力等效剛度和等效阻尼的分析，可以更為深入地認(rèn)識(shí)緣板阻尼結(jié)構(gòu)對(duì)葉片動(dòng)力學(xué)特性的影響機(jī)制。因此本節(jié)采用宏觀滑移模型定性分析緣板阻尼結(jié)構(gòu)關(guān)鍵參數(shù)對(duì)摩擦力等效剛度和等效阻尼的影響規(guī)律，進(jìn)而為第“3”節(jié)結(jié)果的解釋提供依據(jù)。

根據(jù)減振原理，將緣板阻尼結(jié)構(gòu)簡(jiǎn)化為壓緊在振動(dòng)基礎(chǔ)上的自由振子，如圖3所示。一個(gè)質(zhì)量為m的質(zhì)量塊在正壓力N的作用下壓緊在剛性皮帶上。其中，剛性皮帶做簡(jiǎn)諧振動(dòng)，模擬葉片的緣板；而質(zhì)量塊與皮帶間僅通過(guò)摩擦力相互作用，模擬阻尼塊。

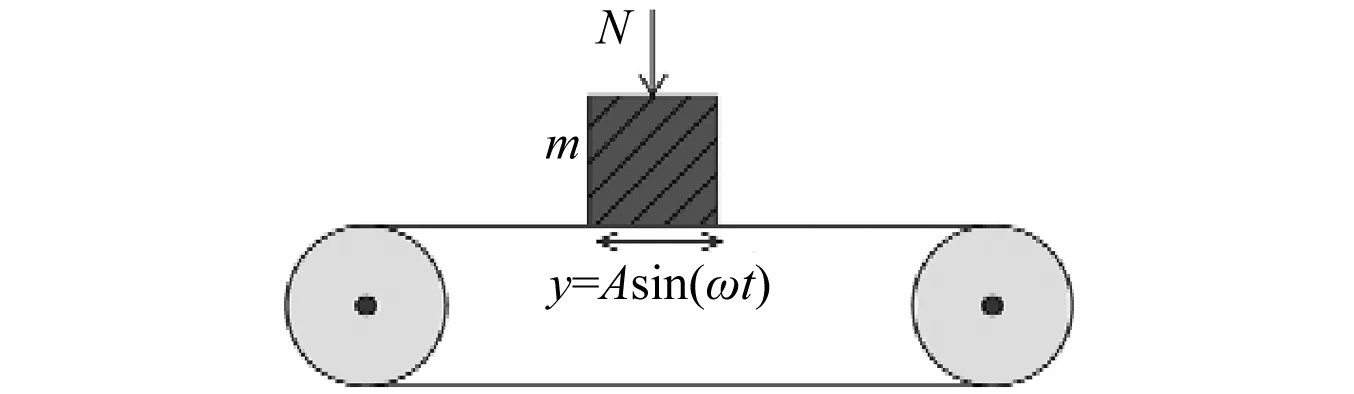
圖3 緣板阻尼結(jié)構(gòu)的簡(jiǎn)化模型Fig.3 A simplified model for UPD

根據(jù)“1.1”節(jié)所述的微分形式的摩擦力學(xué)模型，計(jì)算得到摩擦力時(shí)域內(nèi)的曲線和遲滯回線，如圖4所示。遲滯回線對(duì)角線的連線的斜率反映等效剛度大小，而遲滯回線圍成的面積反映摩擦力的阻尼大小，該面積越大代表耗散能量越多。根據(jù)“1.2”節(jié)所述，可計(jì)算出摩擦力的等效剛度和等效阻尼。

圖4 摩擦力曲線Fig.4 Friction force

2.1 工作正壓力

圖5中給出了正壓力對(duì)摩擦力的等效剛度和等效阻尼的影響規(guī)律。結(jié)果表明：①隨著正壓力增加，摩擦力等效剛度先非線性增加而后趨于某一穩(wěn)定值，其原因在于隨著正壓力增加，振子的滑移位移減小，當(dāng)正壓力到某值時(shí)，振子與皮帶間處于黏滯狀態(tài)，此時(shí)等效剛度不再變化，即為接觸面切向剛度；②隨著正壓力增加，摩擦力等效阻尼先迅速增加后緩慢減小，當(dāng)正壓力達(dá)到250 N時(shí)，其等效阻尼達(dá)到最大值。其原因在于，隨著正壓力增加，摩擦力增加而滑移位移減小，由于摩擦消耗的能量為摩擦力與滑移位移的乘積，當(dāng)正壓力較小時(shí)摩擦力增加占主導(dǎo)因素，表現(xiàn)為等效阻尼增加，當(dāng)正壓力較大時(shí)，滑移位移占主導(dǎo)因素，表現(xiàn)為等效阻尼減小。

最佳阻尼效果對(duì)應(yīng)的正壓力稱為“最佳壓緊力”。

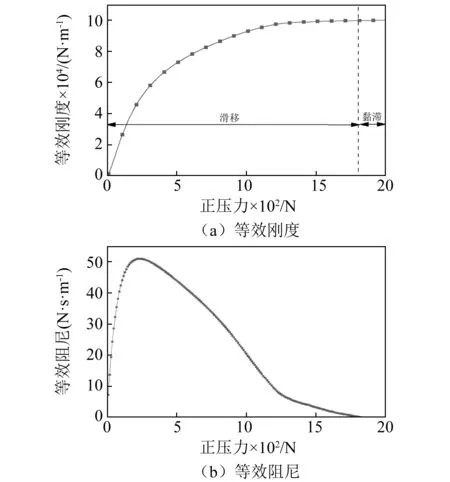
圖5 正壓力的影響規(guī)律Fig.5 The influence of normal load

2.2 質(zhì) 量

摩擦力的等效剛度和等效阻尼在不同相對(duì)質(zhì)量下，隨正壓力的變化規(guī)律如圖6所示。結(jié)果表明：①隨阻尼塊質(zhì)量增加，摩擦力等效剛度減小，達(dá)到黏滯狀態(tài)的正壓力增加，其原因在于正壓力一定時(shí)，阻尼塊的質(zhì)量越大，慣性越大，越難跟隨緣板一起振動(dòng)，與緣板之間的相對(duì)位移越大，進(jìn)而減小了遲滯回線對(duì)角線的連線的斜率，等效剛度越小，越難進(jìn)入黏滯狀態(tài)；②隨阻尼塊質(zhì)量增加，最佳壓緊力增加，最佳壓緊力對(duì)應(yīng)的等效阻尼先增加后基本不變，其原因在于正壓力一定時(shí)，隨著質(zhì)量增加，阻尼塊的相對(duì)位移增加，摩擦力增加，等效阻尼也增加，當(dāng)阻尼塊質(zhì)量增加到一定程度時(shí)，阻尼塊相對(duì)位移基本不變，等效阻尼也基本不變；③隨阻尼塊質(zhì)量增加，具有良好阻尼效果對(duì)應(yīng)的壓緊力范圍越寬，其原因在于阻尼塊質(zhì)量越大，自身慣性越大，越不易進(jìn)入黏滯狀態(tài)，從而可以在較寬的壓緊力范圍內(nèi)產(chǎn)生較大的阻尼。

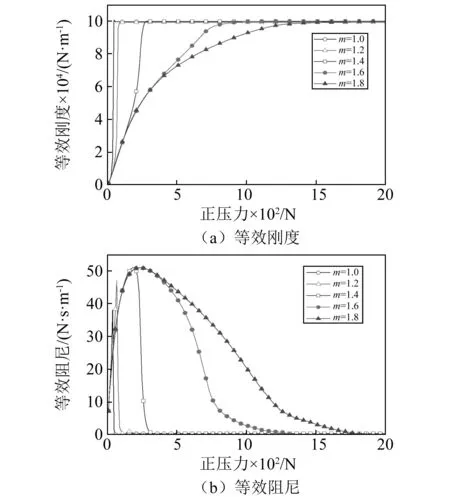
圖6 質(zhì)量的影響規(guī)律Fig.6 The influence of mass

2.3 摩擦因數(shù)

在不同摩擦因數(shù)下，摩擦力的等效剛度和等效阻尼隨正壓力的變化規(guī)律，如圖7所示。結(jié)果表明：①隨摩擦因數(shù)增加，摩擦力的等效剛度增加，達(dá)到黏滯狀態(tài)的正壓力減小，其原因在于正壓力不變時(shí)，隨摩擦因數(shù)增加，摩擦力變大，更易進(jìn)入黏滯狀態(tài)；②隨摩擦因數(shù)增加，最佳壓緊力減小；最佳壓緊力對(duì)應(yīng)的等效阻尼與摩擦因數(shù)基本無(wú)關(guān)。

圖7 摩擦因數(shù)的影響規(guī)律Fig.7 The influence of friction coefficient

3 帶緣板阻尼結(jié)構(gòu)葉片的振動(dòng)特性

本節(jié)進(jìn)一步將有限元法和“1.3”節(jié)所述的分布式接觸摩擦模型相結(jié)合，建立緣板阻尼結(jié)構(gòu)-葉片系統(tǒng)的非線性動(dòng)力學(xué)模型，基于作者已建立的帶有緣板阻尼結(jié)構(gòu)的葉片振動(dòng)響應(yīng)求解方法，研究緣板阻尼結(jié)構(gòu)關(guān)鍵參數(shù)對(duì)葉片振動(dòng)特性的影響規(guī)律，并結(jié)合等效剛度和等效阻尼概念分析其影響的內(nèi)在機(jī)制。

在實(shí)際工作中，輪盤上的葉片為周期對(duì)稱結(jié)構(gòu)，為了減小計(jì)算規(guī)模，在計(jì)算中通過(guò)引入周期性邊界條件，通過(guò)計(jì)算單個(gè)葉片的動(dòng)力學(xué)響應(yīng)獲得所有葉片的響應(yīng)。葉片周期性邊界條件可以表示為接觸面上對(duì)應(yīng)接觸點(diǎn)的摩擦力相等，如式(9)所示。

(9)

圖8為帶緣板阻尼結(jié)構(gòu)的平板葉片有限元模型，葉片榫頭施加位移全約束，葉身施加均布的簡(jiǎn)諧激振力。系統(tǒng)的振動(dòng)方程[23]如式(10)所示

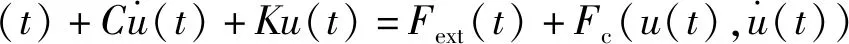
(10)

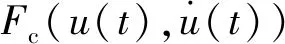
Fext(t)+Fc0

(11)

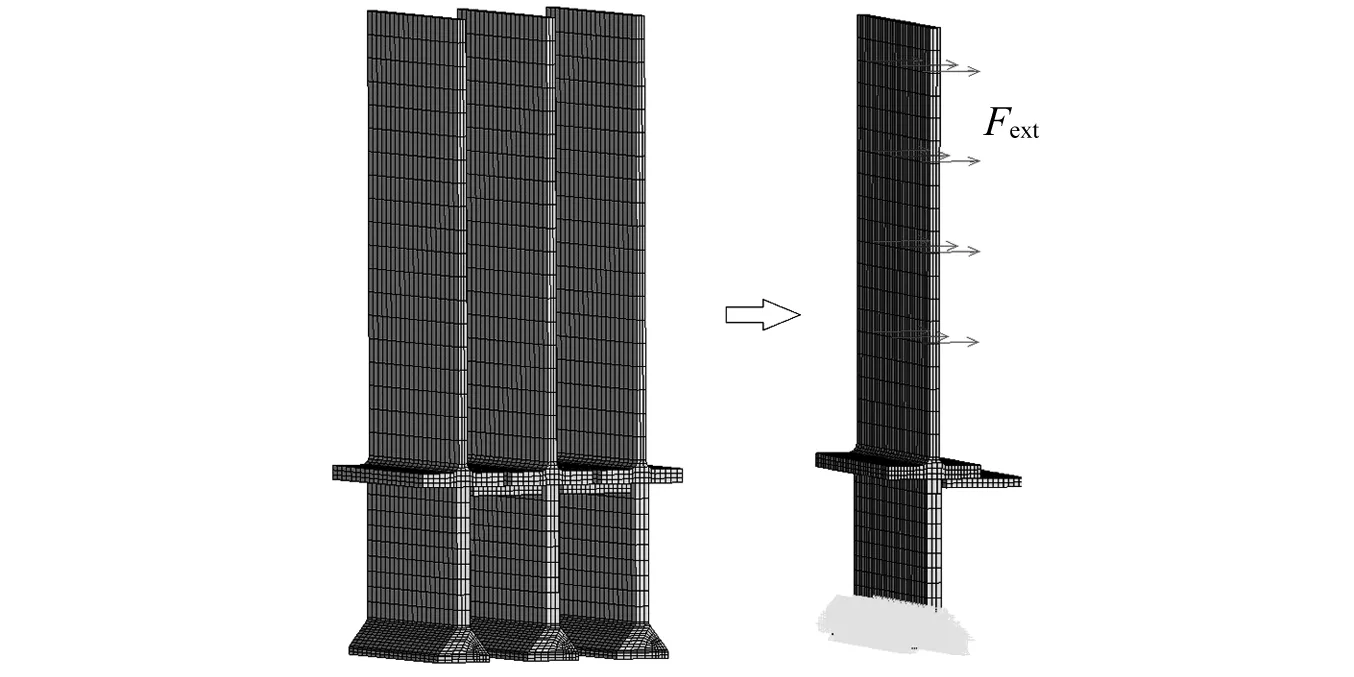
圖8 帶有緣板阻尼結(jié)構(gòu)的葉片的有限元模型Fig.8 Finite element model of blades with UPD

采用如圖9所示的葉片振動(dòng)響應(yīng)求解流程，通過(guò)迭代求解不同參數(shù)下葉片的振動(dòng)響應(yīng)，進(jìn)而得出不同參數(shù)對(duì)葉片的振動(dòng)特性的影響規(guī)律。工程設(shè)計(jì)中，所關(guān)心的葉片振動(dòng)特性包括兩個(gè)方面，一個(gè)是葉片的共振頻率，另一個(gè)是葉片在等幅激振力下的穩(wěn)態(tài)響應(yīng)幅值。

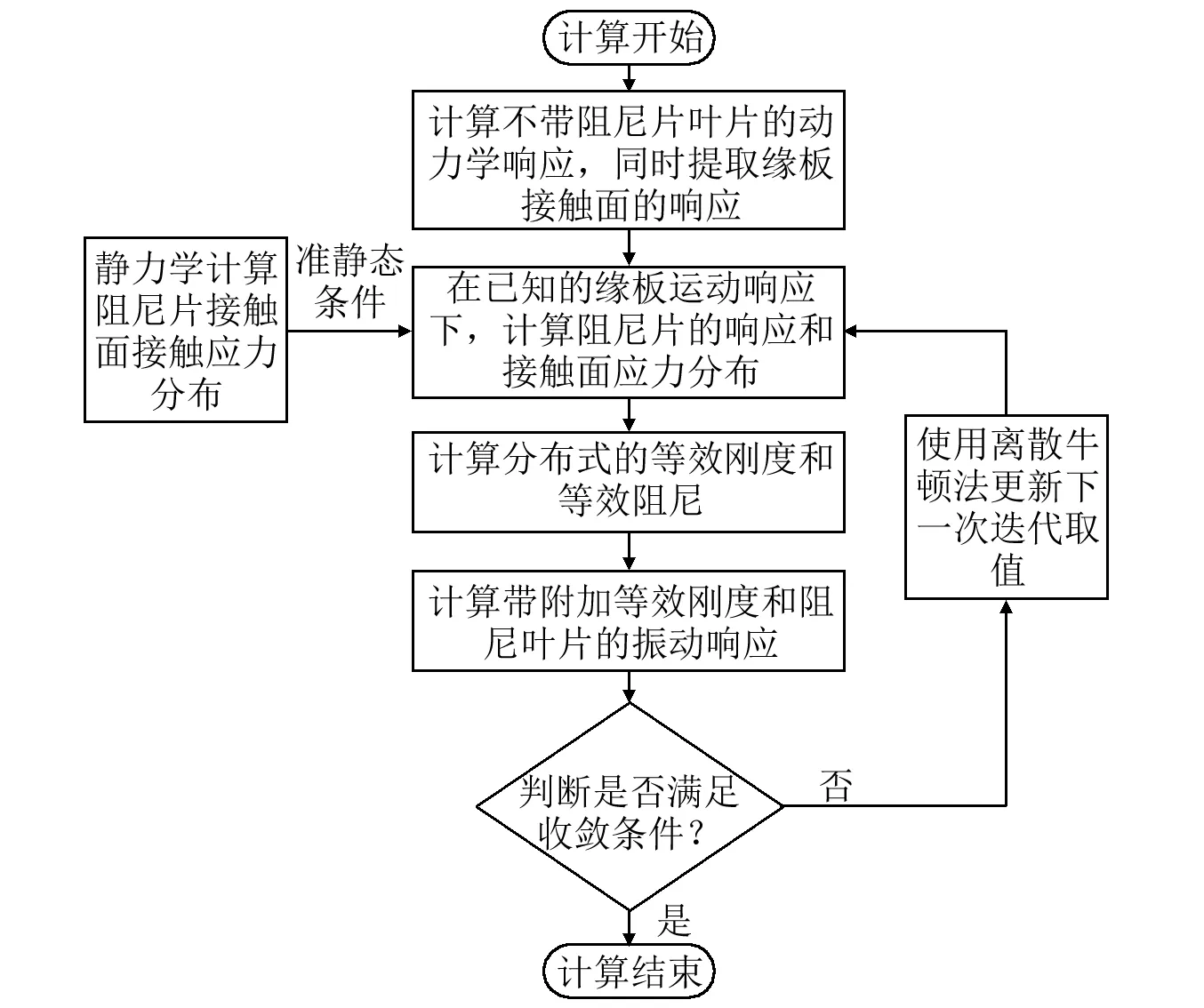
圖9 葉片振動(dòng)響應(yīng)求解流程 Fig.9 Solving process of the vibration response of the blade

3.1 工作正壓力

數(shù)值求解獲得葉片在不同頻率的等幅激勵(lì)下，不同正壓力對(duì)應(yīng)的無(wú)量綱振動(dòng)響應(yīng)幅值，如圖10所示。無(wú)量綱振動(dòng)響應(yīng)幅值定義為振動(dòng)響應(yīng)幅值與不帶緣板阻尼結(jié)構(gòu)的葉片發(fā)生共振時(shí)的響應(yīng)幅值之間的比值。結(jié)果表明，隨阻尼塊所受正壓力增加，葉片的一階共振頻率逐漸升高，葉片的穩(wěn)態(tài)響應(yīng)峰值先迅速減小后緩慢增大。其原因在于隨著正壓力的增加，等效剛度逐漸增加而等效阻尼先迅速增大后緩慢減小。因此，為了保證緣板阻尼結(jié)構(gòu)的最佳減振效果，緣板阻尼結(jié)構(gòu)工作時(shí)的正壓力應(yīng)選為最佳壓緊力或略大于最佳壓緊力。

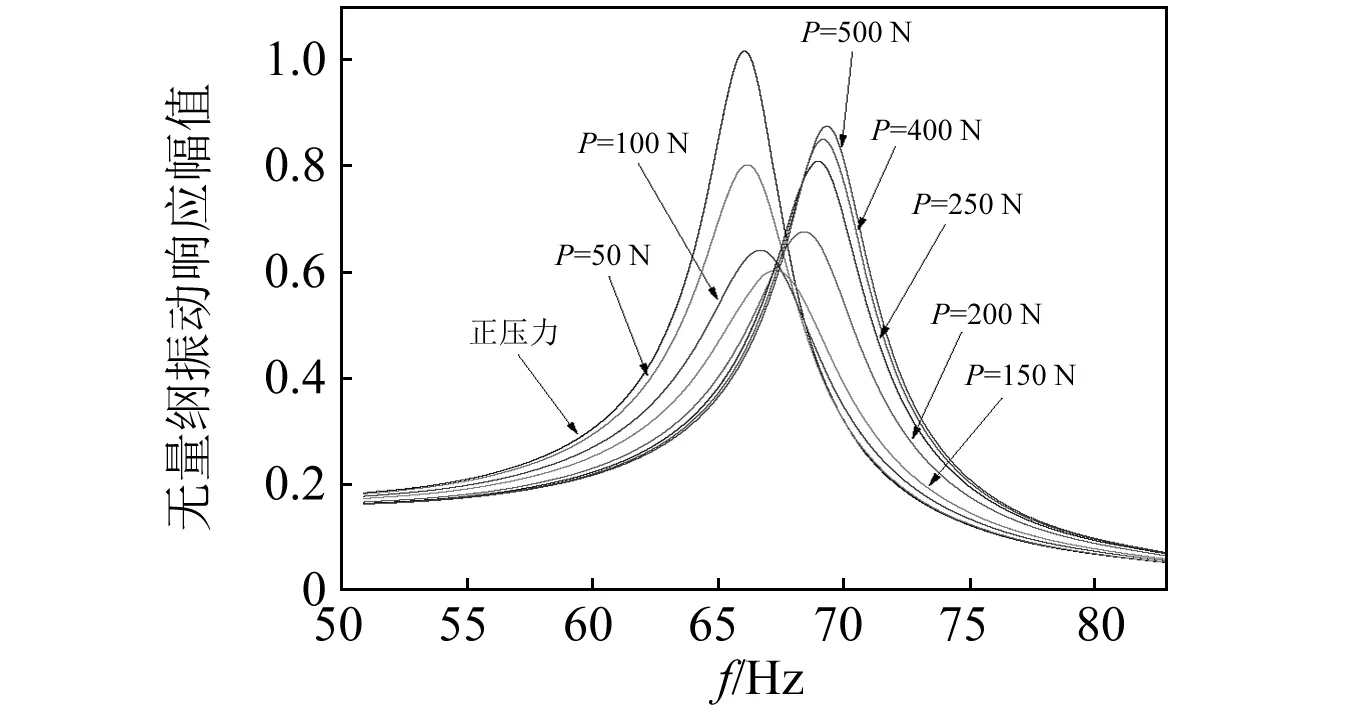
圖10 不同正壓力條件下系統(tǒng)的無(wú)量綱振動(dòng)響應(yīng)幅值Fig.10 Comparison of the curves of normalized frequency response function under different normal load

3.2 質(zhì) 量

通過(guò)數(shù)值計(jì)算獲得了阻尼塊的相對(duì)質(zhì)量對(duì)葉片振動(dòng)特性的影響規(guī)律，如圖11所示。圖11(a)為葉片一階共振頻率的變化規(guī)律，而圖11(b)為無(wú)量綱振動(dòng)響應(yīng)峰值的變化規(guī)律。可見(jiàn)，緣板阻尼結(jié)構(gòu)最佳減振效果可以使葉片振動(dòng)響應(yīng)下降78%。

由圖11可知，阻尼塊的質(zhì)量對(duì)葉片振動(dòng)特性的影響規(guī)律如下：①隨阻尼塊質(zhì)量增加，葉片振動(dòng)頻率減小，其原因在于等效剛度隨著質(zhì)量的增加而減小；②隨阻尼塊質(zhì)量增加，最佳壓緊力增加，最佳壓緊力下的阻尼效果隨著質(zhì)量的增大先增加后趨于不變；③減振效果大于75%對(duì)應(yīng)的正壓力范圍隨著質(zhì)量的增大而增加。

因此，在一定范圍內(nèi)增加阻尼塊的質(zhì)量可以提高最佳壓緊力對(duì)應(yīng)的阻尼效果；當(dāng)正壓力在較大的范圍變化時(shí)，選用較大質(zhì)量的阻尼塊可以獲得較好減振效果。由于阻尼塊的正壓力也與阻尼塊的質(zhì)量相關(guān)，阻尼塊的質(zhì)量應(yīng)根據(jù)工作轉(zhuǎn)速綜合考慮。

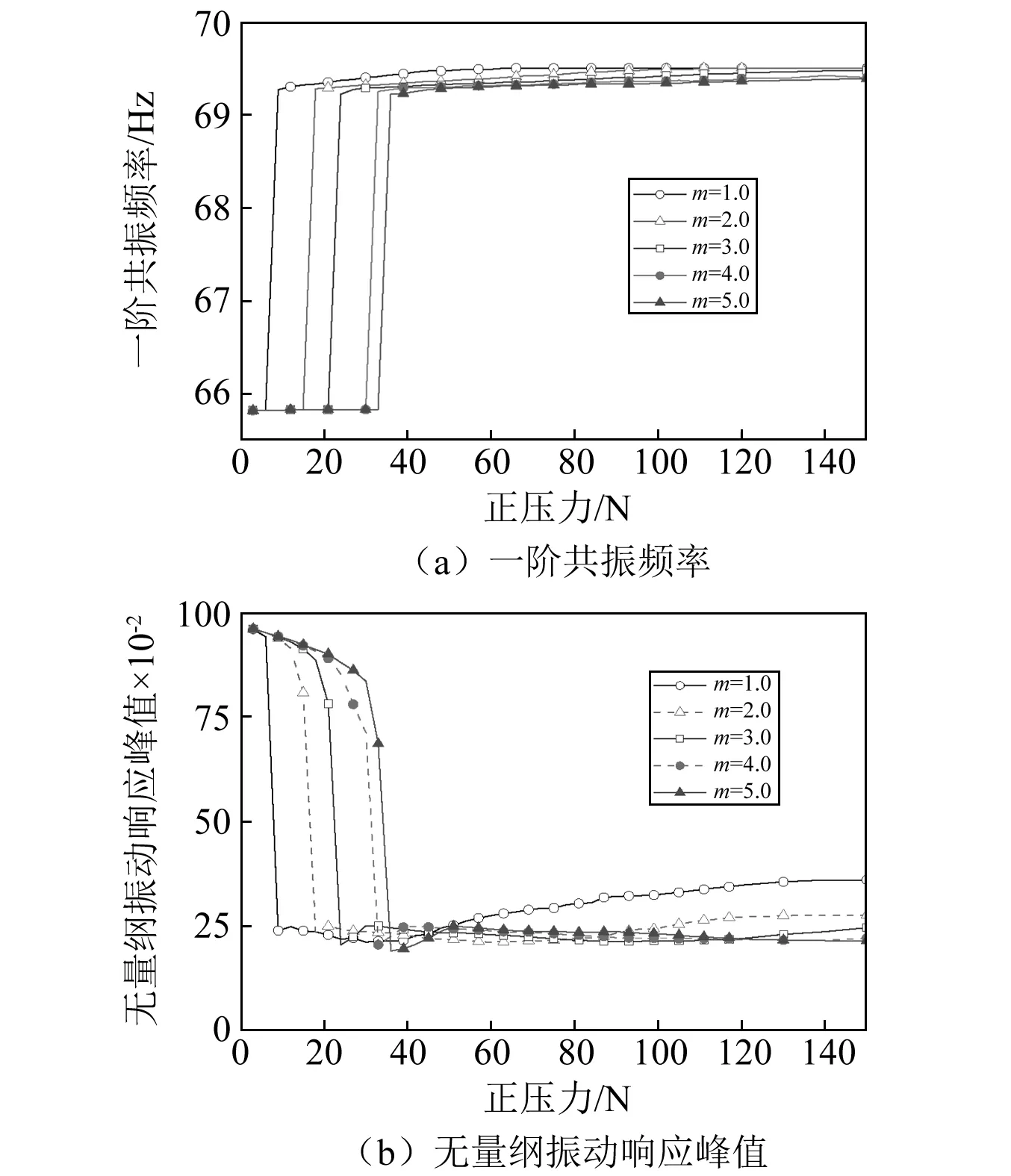
圖11 質(zhì)量對(duì)葉片振動(dòng)特性的影響規(guī)律Fig.11 The influence of mass on the vibration characteristics of the blade

3.3 摩擦因數(shù)

通過(guò)數(shù)值計(jì)算獲得了接觸面的摩擦因數(shù)對(duì)葉片振動(dòng)特性的影響規(guī)律，如圖12所示。由圖12可知：①隨摩擦因數(shù)增加，葉片的共振頻率增加，其原因在于等效剛度隨摩擦因數(shù)增加而增加；②隨摩擦因數(shù)增加，最佳壓緊力減小，最佳壓緊力下的阻尼效果基本不變。③減振效果大于75%對(duì)應(yīng)的正壓力范圍隨著摩擦因數(shù)的增大基本不變。

因此，增大摩擦因數(shù)并不能提高最佳壓緊力狀態(tài)下的減振效果，也不能增加具有良好減振效果時(shí)正壓力的范圍。由于緣板阻尼結(jié)構(gòu)在工作過(guò)程中摩擦因數(shù)會(huì)逐漸減小，應(yīng)選擇較大的正壓力以保證緣板阻尼結(jié)構(gòu)始終具有較好減振效果。

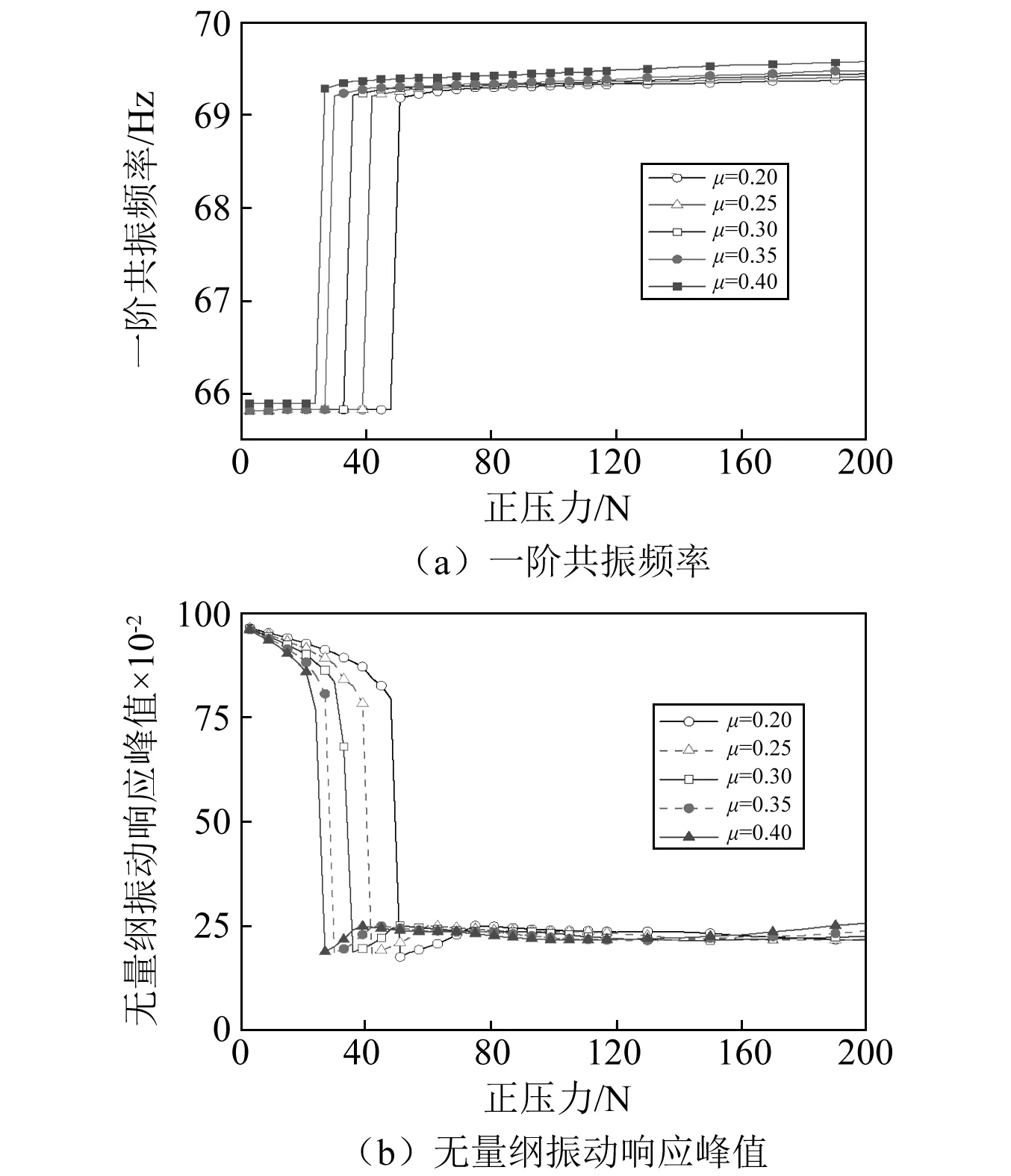
圖12 摩擦因數(shù)對(duì)葉片振動(dòng)特性的影響規(guī)律Fig.12 The influence of friction coefficient on the vibration characteristics of the blade

4 結(jié) 論

本文首先通過(guò)簡(jiǎn)化模型分析了緣板阻尼結(jié)構(gòu)接觸對(duì)剛度和阻尼的影響；然后以帶緣板阻尼結(jié)構(gòu)的平板葉片為研究對(duì)象，采用分布式接觸摩擦力學(xué)模型，分析了緣板阻尼結(jié)構(gòu)關(guān)鍵參數(shù)對(duì)葉片振動(dòng)特性的影響規(guī)律，得出以下主要結(jié)論：

(1)存在最佳壓緊力使得緣板阻尼結(jié)構(gòu)的減振效果最好；通過(guò)優(yōu)化阻尼塊質(zhì)量，可使葉片振動(dòng)響應(yīng)幅值下降78%。

(2)緣板阻尼結(jié)構(gòu)工作時(shí)的正壓力應(yīng)選為最佳壓緊力或略大于最佳壓緊力；最佳壓緊力隨著阻尼塊質(zhì)量的增加而增大，隨著摩擦因數(shù)的增大而減小；最佳壓緊力對(duì)應(yīng)的阻尼效果隨著質(zhì)量的增加先增大后基本不變，且與摩擦因數(shù)的大小基本無(wú)關(guān)。

(3)具有良好減振效果的正壓力范圍隨著質(zhì)量的增大而增大，且與摩擦因數(shù)的大小基本無(wú)關(guān)，因此在設(shè)計(jì)中可適當(dāng)增大阻尼結(jié)構(gòu)質(zhì)量，以提高減振穩(wěn)健性。