辨識主軸轉子系統能量傳遞特性的矢量匹配平衡方法研究

運俠倫，梅雪松，姜歌東，胡振邦，張尊浩

(1.西安交通大學 陜西省智能機器人重點實驗室，西安 710049；2.西安交通大學 機械制造與系統工程國家重點實驗室，西安 710049；3.西安交通大學 機械工程學院，西安 710049)

高端數控機床是一個國家工業制造水平的重要體現，高速高精密的電主軸單元是高端數控機床的核心功能部件。電主軸單元的動態特性會直接影響機床的加工精度和加工效率，但是由于制造材料質量分布不均、裝配因素以及加工過程中的自動換刀等問題都會造成主軸轉子系統存在質量偏心，在高速運轉的過程中，產生的離心力作用會使得主軸轉子系統振動過大，不僅會降低加工質量和加工效率，還會造成噪聲過大，甚至會威脅主軸的使用壽命。如何更加快速、高效的抑制主軸振動將是主軸加工技術的關鍵問題。

旋轉機械的動平衡方法研究由來已久，20世紀20年代，Jeffcott就論證了對轉子系統進行動平衡的必要性。Thearle[1]于1934年首次提出了影響系數法，這是一種試驗方法，通過多次加試重的方式得到轉子系統的加重影響系數，從而實現不平衡量的辨識，這種方法由于簡單有效引起了廣泛的關注，20世紀中葉，Goodman等[2-3]對這一方法都做了詳細的論述和研究。隨著影響系數法在旋轉機械平衡測試中的廣泛應用，國內很多學者對其進行了研究和改進，章璟旋等[4]對最小二乘影響系數法進行了優化改進，雷文平等[5]采用基于雙傳感器的信息融合技術對傳統的影響系數法進行了改進，克服了傳統影響系數法受傳感器安裝弊端的影響。王星星等[6]基于遺傳交叉因子的粒子群優化算法改進了影響系數法，并進行了理論和實驗研究。但是，這種方法需要多次停機，而且頻繁試重也會對高速轉子系統造成不良影響，所以Bishop[7]對以模態理論為基礎的模態平衡法進行了研究，這種方法停機次數少，但是各階模態振型獲取不易，對平衡技術人員素質要求極高。之后，無試重動平衡方法被提出，這種方法不需要通過試重就可以辨識不平衡量的大小和相位，保證了自動化加工過程，可以有效提高加工效率。Gasch對單跨轉子無試重動平衡方法進行了深入的研究，通過將不平衡量作為模態參數進行識別實現了不平衡參數辨識。賓光富等[8]基于動力學模型對多跨轉子軸系的無試重動平衡方法進行了研究，并且采用最小二乘法求取了平衡配重。張西寧等[9]基于粒子群平衡配重優化技術提出了軸系全息平衡方法。章云等[10-11]基于動力學模型和模態分析理論也提出了無試重動平衡方法，對轉子質量連續分布的機床主軸的不平衡識別做了研究。

上述方法有些需要多次啟停試重，有些過程繁瑣，計算量大，實用性不強。本文通過建立試驗轉子系統有限元動力學模型，通過動力學模型與模態試驗快速辨識主軸轉子系統的能量傳遞特性，通過能量傳遞系數計算出不平衡矢量，利用矢量合成原理對配重質量和配重方位進行尋優匹配，可以快速、高效的實現主軸轉子系統平衡，對于實現智能化、自動化加工過程具有重要的意義。

1 主軸轉子系統傳遞特性辨識原理

主軸轉子系統可以離散為多自由度系統，由于存在不平衡激勵，轉子在高速轉動時會產生慣性離心力，從而持續強迫轉子振動。如式(1)所示為主軸系統動力學微分方程

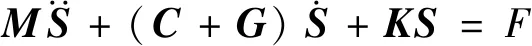
(1)

式中：M為系統的質量矩陣；C為阻尼矩陣；G為陀螺矩陣；K為剛度矩陣；S為廣義坐標矢量，此處為系統的位移向量；F為作用在轉子上的廣義力，此處為由不平衡激勵引起的離心力。假設轉速為ω，那么不平衡激振力可以表示為

F=u·ejω·t

(2)

聯立式(1)和式(2)，易得不平衡振動響應S為

S=r·e[j(ω·t+φ)]

(3)

式中：r和u分別為不平衡響應和不平衡量；φ為滯后角。聯立式(1)～式(3)可得

α-1·r=u

(4)

α=[K-ω2M+Gω+iωC]-1·e(-jφ)

(5)

式中：α為加重影響系數矩陣。

由式(5)可知，轉子軸系的加重影響系數是由質量、剛度、滯后角以及轉速共同決定的，也就是說轉子軸系的加重影響系數是由轉子結構參數所決定的，是反映轉子系統能量傳遞特性的固有參數。因此，通過建立準確的動力學模型獲取轉子結構的特征參數，則可以實現轉子傳遞特性的準確辨識，從而根據求得的加重影響系數矩陣則可以計算平衡矢量為

Q=-α-1·A

(6)

式中：Q為平衡矢量；A為特定轉速下拾取的不平衡振動響應矢量，負號為平衡矢量Q與不平衡矢量之間的相位相差180°。由于配重盤上的配重孔方位固定，同時配重螺釘質量有限，所以在獲得轉子軸系的動力學能量傳遞系數后，應用矢量合成原理對配重質量和配重方位進行尋優匹配，能夠非常快速的獲取準確、有效的配重方案。計算流程圖如圖1所示。

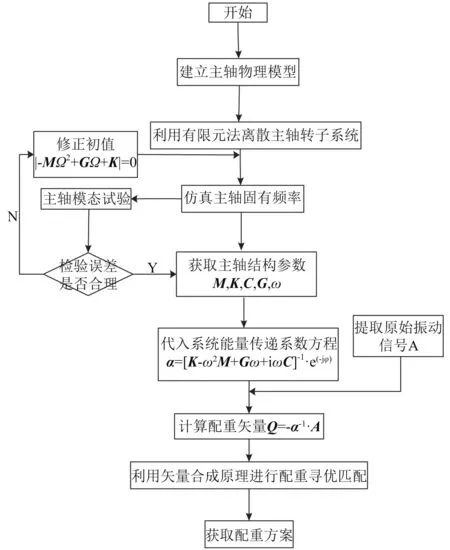
圖1 矢量匹配平衡方法流程圖Fig.1 Schematic diagram of vector matching balance method

2 主軸轉子系統有限元建模

轉子軸系是電主軸的核心部分，軸系主要有轉子和軸承組成，但是由于電主軸內部結構復雜，所以軸系通常進行階梯式設計來滿足主軸內部的結構設計。本課題組設計的實驗電主軸180SD35Q15的物理模型，如圖2所示。

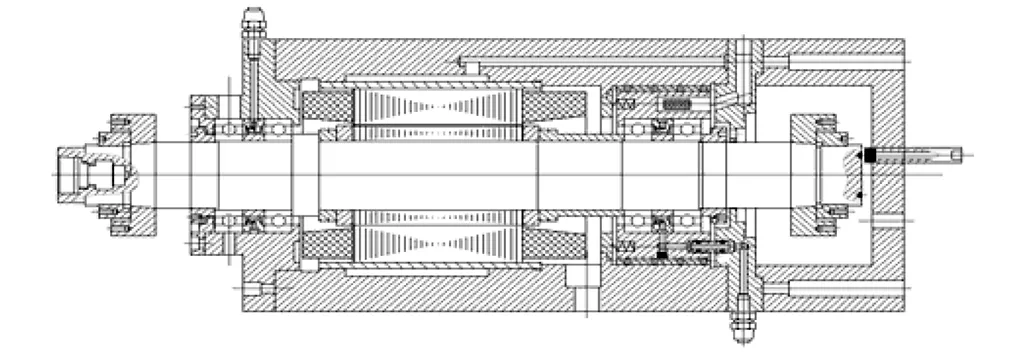
圖2 電主軸180SD35Q15的模型Fig.2 180SD35Q15 model

電主軸轉子部分進行離散化處理，可以將其沿軸線方向劃分為圓盤、軸段和軸承座等單元，圓盤質量單元的運動廣義坐標為其與軸段配合處，軸段單元處的節點的位移向量{u1d}=[x,qy]T和{u2d}=[y,-qx]T。則圓盤運動微分方程為

(7)

式中：[Md]為圓盤質量矩陣；[J]為陀螺矩陣；{Q1d}，{Q2d}為相應的廣義力，包括兩端彈性軸所作用的力和力矩。彈性軸段單元的廣義坐標是兩端節點的位移，即

(8)

軸段單元的運動微分方程為[12]

(9)

式中：[Ms]為軸段質量單元矩陣，[Ms]=[MsT]+[MsR]；[Js]為軸段回轉矩陣；[Ks]為軸段單元剛度矩陣；{Q1s}，{Q2s}為廣義力向量，它包括相鄰軸段的作用力和力矩。當軸段單元有連續分布的偏心距ex(s)和eh(s)時，則還包括不平衡廣義力。

建立軸承的擬靜力學分析模型，通過牛頓-拉夫遜法求得主軸軸承參數初值[13]，通過模態測試實驗和頻率方程對初值進行修正，為主軸傳遞特性的精確辨識提供準確的轉子系統結構參數。對于主軸坐標系而言，在x-z平面內，軸承作用于軸頸節點處的廣義力是

(10)

如不考慮軸承座的等效質量，則系統的位移向量為

(11)

綜合圓盤及軸段單元的運動微分方程，可得到主軸轉子系統的運動微分方程

(12)

對于質量矩陣[M]、回轉矩陣W[J]和剛度矩陣[Kx]，[Ky]，其組裝時按節點自由度順序組裝。利用上述的方法對圖2所示的實驗室主軸進行有限元建模，可以將轉子劃分為70個節點，形成69個單元，以轉子軸心為軸建立相應坐標系，則轉子系統的有限元模型，如圖3所示。

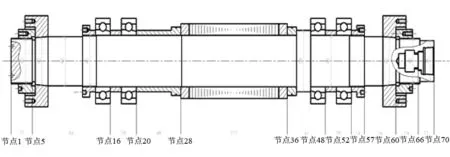
圖3 主軸轉子系統的有限元動力學模型Fig.3 Finite element model of spindle rotor system

3 實驗分析與驗證

3.1 主軸模態測試

應用同側激勵同側拾取響應的錘擊法對主軸動力學模型進行實驗驗證[14]，如圖4(a)所示為轉子系統固有頻率測試實驗示意圖，頻響函數計算采用功率譜函數進行計算，計算原理為

(13)

式中：H(ω)為頻響函數；S(ω)為輸入信號；F(ω)為輸出信號；*為共軛；GSF=S(ω)F*(ω)為對應時間信號的互功率譜函數；GFF=F(ω)F*(ω)為對應時間信號的自功率譜函數。

圖4 主軸轉子系統固有頻率測試Fig.4 Natural frequency test

如圖4(b)所示為實驗測試結果，與計算結果的對比分析見表1，從表1可知，計算結果和實驗結果非常接近，證明仿真效果良好，從而說明動力學仿真參數具有可信度，可以用來計算轉子系統的能量傳遞系數。

表1 固有頻率的仿真和試驗對比分析Tab.1 Comparison between simulation and experiment of natural frequency

3.2 主軸轉子系統動平衡實驗

根據本文提出的動平衡方法在前文提到的主軸動平衡實驗臺上進行實驗驗證，測試示意圖如圖5所示。主軸型號為180SD35Q15，主軸前端伸出端設置有配重盤，沿圓周方向均勻分布12個配重螺紋孔，用來實現主軸轉子的平衡配重,實驗轉速為18 000 r/min。

圖5 主軸系統動平衡實驗Fig.5 Dynamic balance experiment

首先通過有限元建模獲取主軸轉子系統的結構參數，并代入式(5)，得到主軸轉子系統的動力學能量傳遞系數為K=-4.323 6+0.159 3i,利用矢量合成原理對配重方位和配重質量尋優搜索，就可以快速得到配重為7 g·mm∠240°，10.5 g·mm∠0°，在對應的配重孔上添加配重。不平衡特征主要表現在工頻上，如圖6(a)所示為采集的原始信號。由圖6(a)可知，原始信號中混疊了很多其他成分，必須對原始信號進行濾波降噪處理，本文采用諧波小波對原始信號進行濾波降噪處理，濾波后的工頻時域原始信號如圖6(b)所示。

如圖7所示為原始時域信號、無試重方法配重后時域信號以及兩次影響系數法平衡后的時域信號對比圖，從圖中可以看出，兩次影響系數法和矢量匹配法都顯著的降低了振動，顯然，矢量匹配法的效果更好。

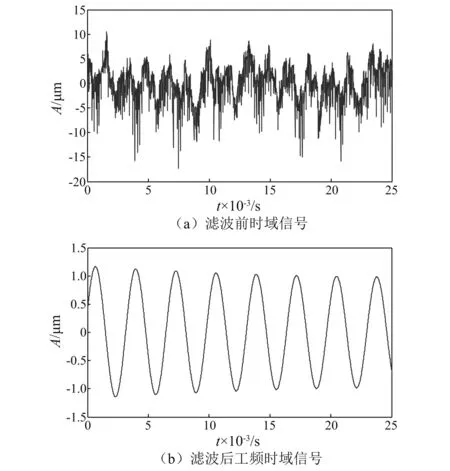
圖6 信號濾波前后對比Fig.6 Signal filtering

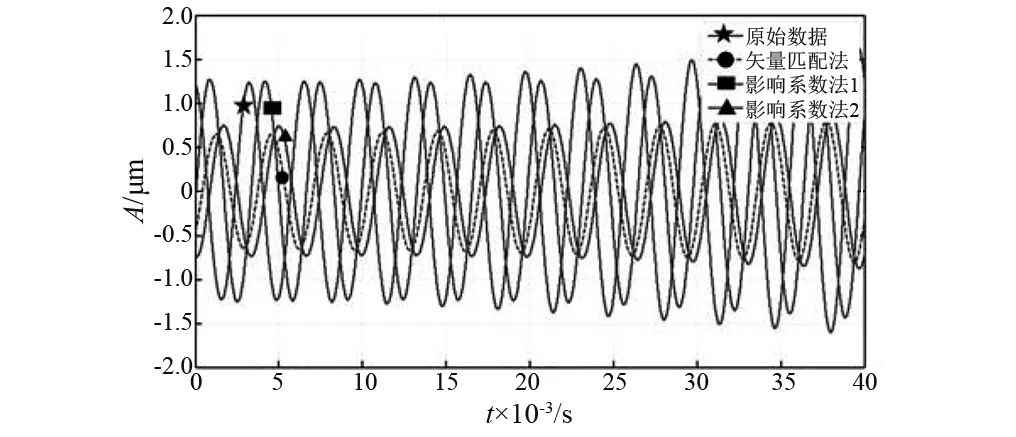
圖7 平衡前后時域信號對比Fig.7 Comparison time domain signal balancing before and after

如圖8所示為濾波后原始信號、影響系數法以及無試重方法的工頻幅值對比。從圖8可知，第一次采用影響系數法進行配重，振動幅值由原始的1.566 μm下降到1.459 μm，下降幅度為6.83%，抑振效果不明顯，重新調整試重后進行第二次影響系數法配重，振動幅值由原始的1.566 μm下降到0.945 3 μm，下降幅度為39.64%。而采用本文所述的矢量匹配平衡方法振動幅值從1.566 μm下降到0.789 8 μm，下降幅度達到49.57%，抑振效果相較于影響系數法更好，而且無需試重，一次配重成功，有效的縮短了平衡時間。

圖8 兩種方法平衡前后工頻幅值對比Fig.8 Comparison of two methods before and after balance

如圖9所示為提取原始信號、無試重方法配重后以及兩次影響系數法配重后軸心軌跡對比圖。從圖9可知，無試重方法在X，Y兩個方向上都顯著降低了工頻振動幅值，相較于影響系數法，無試重方法在兩個方向上的效果都非常明顯。

圖9 工頻軸心軌跡對比Fig.9 Comparison of axis orbit

此外，分別在15 000 r/min和21 000 r/min時進行了矢量匹配平衡方法和影響系數法的對比實驗研究，實驗結果歸納如表2所示。

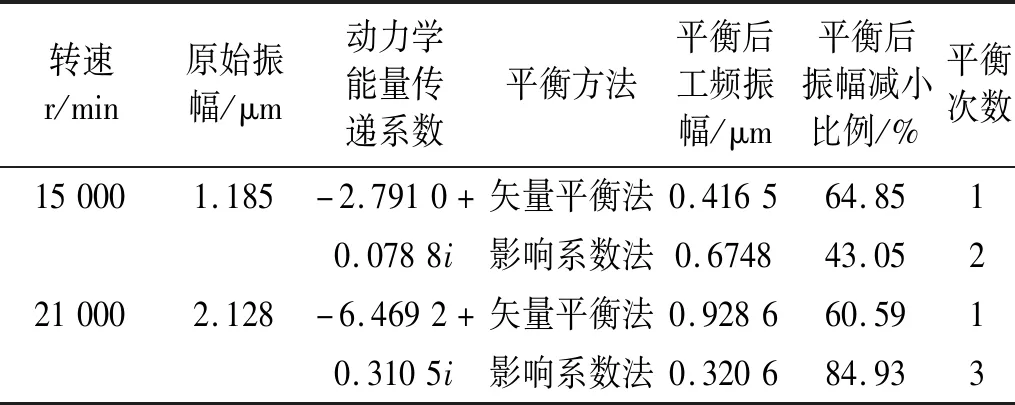
表2 矢量匹配平衡法和影響系數法對比實驗Tab.2 Comparison experiment of vector matching balance method and influence coefficient method

從表2可知，在15 000 r/min和21 000 r/min時，采用矢量匹配平衡方法可以有效的抑制振動，振幅下降比例分別達到64.85%和60.59%，無需試重且只需一次配重，效率非常高；與之相對應的影響系數法振幅下降比例分別為43.05%和84.93%，雖然影響系數法在21 000 r/min時平衡精度較好，但是由于試重的限制，需要分別進行2次和3次試重配重，平衡效率低下。

4 結 論

抑制主軸振動可以有效改善加工質量，完善自動化加工環節，提高加工效率，動平衡方法的研究對提高旋轉機械的運轉特性具有重要的意義。本文通過推導證明了加重影響系數其實是由系統本身結構所決定的，能夠反映系統能量傳遞特性的參數，因此提出了利用動力學模型辨識轉子傳遞特性的矢量匹配平衡方法，結論如下：

(1)轉子加重影響系數是由轉子結構特性參數所決定，是能夠反映轉子系統的能量傳遞特性的參數。應用轉子結構特征參數精確辨識轉子傳遞特性，聯立采集的初始振動就可以計算得到不平衡量，并且利用矢量合成原理尋優匹配，可以快速獲取有效的配重方案。

(2)針對180SD35Q15高速磨削主軸建立了有限元模型，并且利用模態測試試驗修正了轉子系統的模型。

(3)分別在15 000 r/min，18 000 r/min以及21 000 r/min時進行了影響系數法和矢量匹配平衡方法的對比實驗，發現相較于影響系數法，矢量匹配平衡法優勢盡顯，不僅平衡精度很好，而且不需要試重，只需一次配重就可以實現主軸振動抑制，平衡效率很高。

此外，這種方法可以在不停機的情況下進行多次平衡，逐步降低不平衡振動，因此其非常適用于噴液式等加重式的在線動平衡系統，可以大大的提高在線平衡時的效率和精度，這也是我們課題組下一步的研究工作。