采樣長度對阻尼識別的影響

閆 凱，趙曉丹，連海平，程 惠，孫黎明

(1.江蘇大學 汽車與交通工程學院，江蘇 鎮江 212013；2.洛陽拖拉機研究所有限公司 拖拉機動力系統國家重點實驗室，河南 洛陽 471039)

阻尼表征振動衰減與能量耗散程度，是決定結構動力特性的重要參數[1]。準確識別結構的阻尼值，可以提高動力分析結果的可靠性；而阻尼值變化的準確識別，還可用于發現結構產生的細小裂紋等故障診斷方面。工程應用中，識別不準的阻尼值也會給很多方面的研究帶來問題，識別精度不高會限制阻尼識別在故障診斷等方面的應用，提高阻尼識別精度一直是學者們所關心的焦點。目前阻尼識別的方法主要有：使用多單元傳遞函數方程計算阻尼值的傳遞函數法[2]；融合大容量數據譜分析技術和頻域任意區間聚焦細化技術的大容量數據譜分析法；通過局部頻率細化頻率提高阻尼識別精度的細化與大容量數據采集分析法[3]；通過線性插值法近似確定頻譜函數圖像中半功率點進而計算阻尼值的半功率帶寬法及其改進方法等[4-5]，此類阻尼識別方法都以傅里葉變換作為理論基礎。傅里葉變換受截斷誤差影響[6]，導致阻尼識別結果精度降低，尤其當識別阻尼值較小時，由于其固有頻率附近譜峰較窄[7-8]，時域截斷造成的能量泄漏對阻尼識別影響增加，為減小這一影響，使用增大采樣長度的方法以減小截斷誤差[9]。傅里葉變換理論分析是當積分時段趨向于無窮時截斷誤差為零，同時時間趨向于無窮時噪聲頻譜的期望值也為零，受這二點理論分析的影響容易形成采樣時間越長，阻尼識別精度越高的結論，進而在工程實踐中指導阻尼識別使用長數據分析。如在阻尼識別應用中，陳正林[10]使用采樣時間為20 s、采樣點數為20 000的長數據對曲軸阻尼進行識別；在橋梁領域，劉漢夫[11]提出應盡可能的增大數據采樣量，采用更長的數據分析來保證阻尼分析結果的可靠。

在工程領域中，對信號的采集不可避免的會存在著隨機噪聲的干擾[12]。對工程信號作傅里葉變換的同時，噪聲信號也在作積分運算，以采樣分析時間到無窮得出采樣越長識別精度越高的結論沒有考慮到噪聲信號隨振動衰減信號一同被積分時的變化關系，本文考慮這一細節，分析了振動衰減信號和噪聲信號頻譜隨采樣點數的比例關系，得出當采樣點數超過某一臨界值時，噪聲頻譜幅值會高于振動衰減信號頻譜幅值，此時將導致阻尼識別精度下降，對所做的分析進一步使用仿真計算及懸臂梁實驗進行了驗證。

1 理論分析

設存在一工程信號

x(t)=x0(t)+xn(t)

(1)

式中：x0(t)為振動衰減信號；xn(t)為隨機噪聲干擾信號。

1.1 振動衰減信號頻譜分析

振動衰減信號復數形式表示為

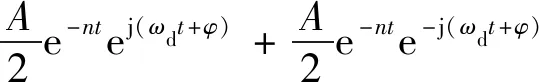
(2)

式中：A為信號振幅；n為信號衰減系數；ωd為有阻尼固有頻率。為方便分析，將相位角φ取值為零。

對x0(t)做傅里葉變換，當頻率ω=ωd時，振動衰減信號取得頻譜幅值，其傅里葉變換可以表示為

(3)

(4)

采樣時間T，采樣頻率fs與采樣點數N存在以下關系

(5)

將式(5)代入式(4)，振動衰減頻譜幅值可以表示為

(6)

分析式(6)可知該函數為單調遞減函數，當nT取值為4.6時，e-nt值為0.01，即(1-e-nt)≈1，故當T≥4.6/n時，振動衰減信號頻譜幅值為

(7)

1.2 噪聲信號頻譜分析

對噪聲干擾信號xn(t)作時域-頻域轉換，得到噪聲干擾信號的幅頻關系。設工程信號中的噪聲干擾信號xn(t)服從正態分布N(0,σ2)，記為向量xn，將噪聲向量xn與傅里葉變換基向量ek進行內積運算[14]，結果表示為Z(ω)

(8)

分析式(8)，噪聲干擾xni為服從正態分布的隨機信號，且獨立正態分布隨機變量的線性組合仍然具有正態分布的特性[15]，故Z(ω)是一個服從正態分布的隨機函數。對Z(ω)的實部求期望得

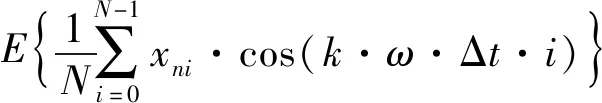
(9)

噪聲干擾信號xni服從正態分布N(0,σ2)，即E{xni}=0，可得其實部的期望值也為零

E{Re(Z(ω))}=0

(10)

對Z(ω)實部求方差得

(11)

由統計學分析知，服從正態分布N(0,σ2)的隨機噪聲xn，當i≠j時

E{xni·xnj}=0

(12)

當i=j時

(13)

將式(12)、式(13)代入式(11)，化簡得

(14)

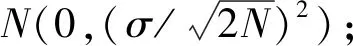
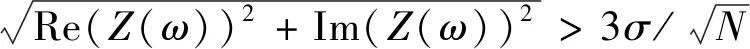
(15)

(16)

1.3 噪聲對阻尼識別的影響

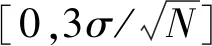
(17)

2 模擬及計算分析

為了更清晰的反映采樣長度對阻尼識別的影響，使用模擬仿真對其進行了計算分析。給出一受噪聲污染的信號

x(t)=2e-ntcos(ωdt)+xn(t)

(18)

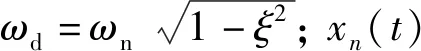
阻尼識別結果如表1所示。從阻尼識別結果看，相比之下內積法阻尼識別精度較半功率帶寬法高；兩種阻尼識別方法都在2 000采樣點附近有較高的識別精度；兩組阻尼識別結果的相對誤差都存在先減少后增大趨勢。說明并非采樣點數越多，阻尼識別精度越高。

表1 仿真計算阻尼識別結果Tab.1 Damping recognition results of simulation

圖1為采樣點數分別為500點、2 000點、8 000點和32 000點時信號x(t)所對應的頻譜圖。由x(t)的頻譜圖分析可得，當采樣點數為500點時，采樣時間T為0.25 s，小于4.6/n，此時截斷誤差大，導致阻尼識別結果誤差較大。采樣點數為2 000點時，此時采樣點數增大，采樣信號的截斷誤差減小，且噪聲信號對真實響應信號干擾較小，阻尼識別結果誤差小。采樣點數為8 000點時，噪聲信號對真實響應信號干擾開始增大，阻尼識別結果誤差增大。采樣點數為32 000點時，此時采樣點數已超出由式(17)計算得出的臨界采樣點數31 304點，噪聲信號對真實響應信號干擾大，阻尼識別結果已經偏離實際值。

圖1 信號x(t)頻譜圖Fig.1 Signal x(t)spectrum diagram

3 懸臂梁阻尼測試實驗

工程應用中很多結構都可以簡化為梁式結構，而懸臂梁結構是其中常見的類型。從工程應用角度出發，選取了懸臂梁結構做阻尼測試實驗。實驗裝置圖如圖2所示。選取一根鋼質懸臂梁，其具體的參數為：懸臂梁長寬高分別為1 000 mm，50 mm和14 mm；懸臂梁固定端用螺栓和壓板緊固在試驗臺架上，用銅質力錘錘擊懸臂梁，通過安裝在末端的加速度傳感器測得自由端振動信號。

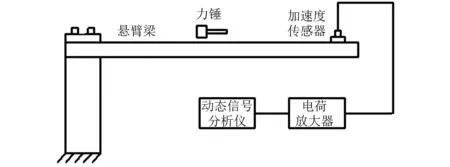
圖2 實驗裝置簡圖Fig.2 Experimental device diagram

對自由端振動信號進行數據采集，采樣頻率為5 000 Hz。采樣點數為5 000點時，其信號頻譜圖如圖3所示。由圖可看出懸臂梁響應信號模態主要有六個，分別為約10 Hz，約60 Hz，約200 Hz，約400 Hz，約600 Hz及約900 Hz。此處以約200 Hz模態為例，采用半功率帶寬法和內積法進行阻尼識別。

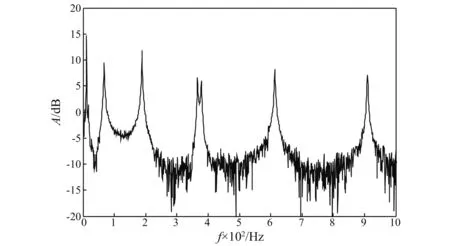
圖3 懸臂梁響應信號頻譜圖Fig.3 Cantilever response signal frequency spectrum

分別以5 000點和25 000點采樣點數對約200 Hz模態進行阻尼識別，結果如表2所示，不同采樣長度對應的阻尼識別結果有差別。

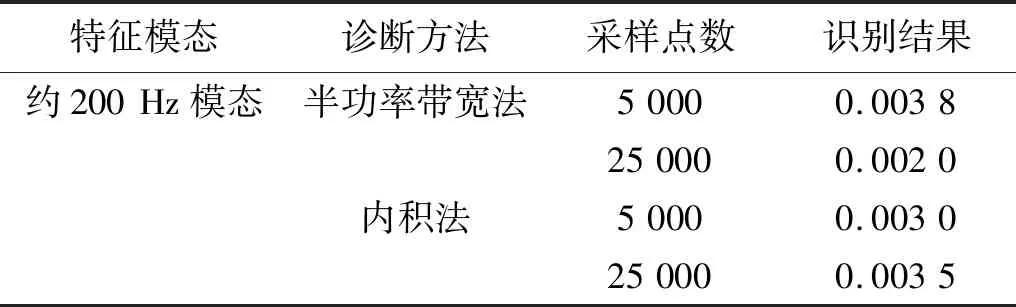
表2 懸臂梁200 Hz附近模態阻尼識別結果Tab.2 Damping identification results of the cantilever beam modal near 200 Hz

為確定準確的阻尼值，識別出該模態參數后，以此參數構造出阻尼識別信號，并從總信號中將此估計信號減去，當識別結果準確時，剩余信號頻譜中對應頻率附近能量變得很小，剩余頻譜圖里觀察不到明顯峰值。仿真算例已經驗證內積法相比與半功率帶寬法有著更高的識別精度，此處以內積法為例，分別將5 000采樣點和25 000采樣點時所識別出的約200 Hz模態信號從原信號中減去，剩余信號頻譜如圖4所示。從圖4可知，采樣點數為5 000點時，減去識別阻尼信號后，剩余信號200 Hz附近觀察不到明顯峰值，此階模態信號已被剔除；采樣點數為25 000點時，減去識別阻尼信號后，剩余信號200 Hz附近仍然可以觀察到明顯峰值。

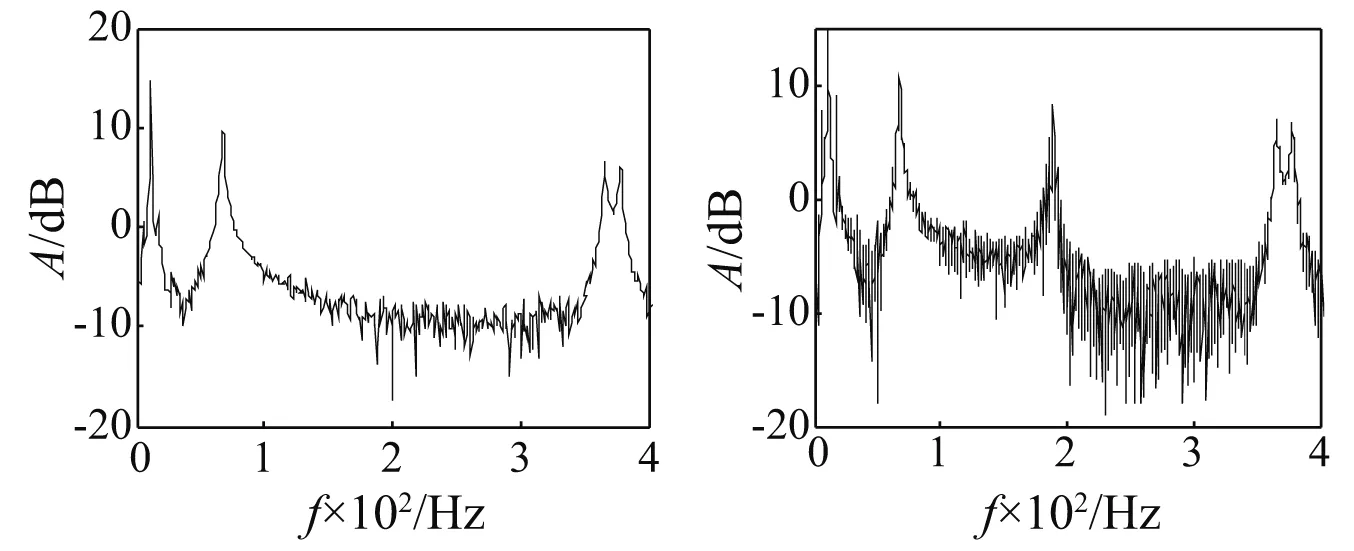
圖4 懸臂梁200 Hz附近剩余信號頻域對比圖Fig.4 Remainder signal contrast frequency domain diagram near 200 Hz of the cantilever beam

由懸臂梁阻尼識別實驗可以看出，當采樣點數為5 000點時，此時阻尼識別精度已經很高，模態信號能夠被準確識別出；采樣點數繼續增加到25 000點，此時受噪聲干擾影響增大，誤差反而增大，阻尼識別結果不夠準確，故增加采樣點數不一定能提高阻尼識別精度，進一步驗證了本文的結論。

4 結 論

(1)當傅里葉積分時段趨近于無窮時，噪聲頻譜期望值為零，但是其實際發生值不是期望值，而是主要在零與三倍標準差之間浮動，對阻尼引起的振動衰減信號的識別不能忽略噪聲頻譜實際發生值對振動衰減信號的影響，根據期望值為零得到采樣點數越多識別結果越精確這一觀點不適合于阻尼診斷。

(2)適當增加采樣點數可以提高阻尼的識別精度，但采樣點數并不是越多越好，采樣點數超過臨界值取值會導致診斷出的結果與理論值誤差不降反升。

(3)通過仿真計算及懸臂梁結構敲擊實驗表明采樣點數過多時阻尼識別精度反而降低，驗證了本文的理論分析。建議阻尼識別采樣點數不超過臨界值取值，為工程應用中采樣點數的選取提供參考。