三階微分方程組特解的待定矩陣法

吳幼明，林曉瑩

（佛山科學技術學院 數學與大數據學院，廣東 佛山 528000）

求微分方程組特解[1-8]的方法是微分方程理論的重要內容之一，國內外許多學者已做過大量的研究，得到了很多簡捷實用的研究成果.文獻[5-7]分別給出了方程組Af″-Bf=t(x),Af″-aAf′-Bf=t(x)和Af″-Bf′-Af=t(x)在t(x)=(acosβx+bsinβx)·eαx的形式時的特解公式.文獻[8]以算子法為基礎，窮舉法為輔助，對三階方程Af?-Bf=0在8種情況下的通解形式進行了詳盡的推導和歸納，但未對特解進行討論.本文在文獻[5-8]的基礎上，采用待定矩陣法，給出了方程組Af?-aAf′-Bf=t(x)當t(x)=(acosβx+bsinβx)·eαx的形式時的特解公式.本文方程比文獻[5-7]的方程階數更高，是文獻[5-7]的推廣.此外，本文的方程比文獻[8]的方程多了一階導數項且為非齊次方程，是文獻[8]的補充，因此更具有普遍性.

1 符號

給出矩陣微分方程

其中，fi=fi(x)(i=1,2)是關于x的函數，ti(x)(i=1,2)是關于x的三角函數與指數函數的乘積，a,aij,bij(i,j=1,2)是常數.

因此，方程（1）整理后為

2 方程組的特解

對于矩陣微分方程（2），設

其中，ai,bi,αi,βi(i=1,2)是常數.

根據待定矩陣法，可設方程（2）的1個特解為

將式（4）代入方程（2）中，整理并比較同類三角函數的系數得

由式（5）取第i(i=1,2)列比較得

由式（6）取第i(i=1,2)列比較得

將式（7）代入式（8）中整理得

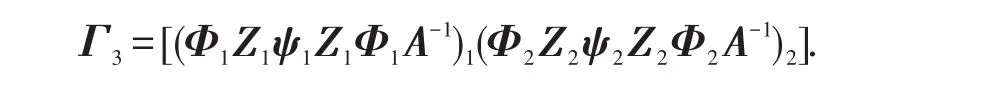
所以，矩陣微分方程（1）的1個特解為

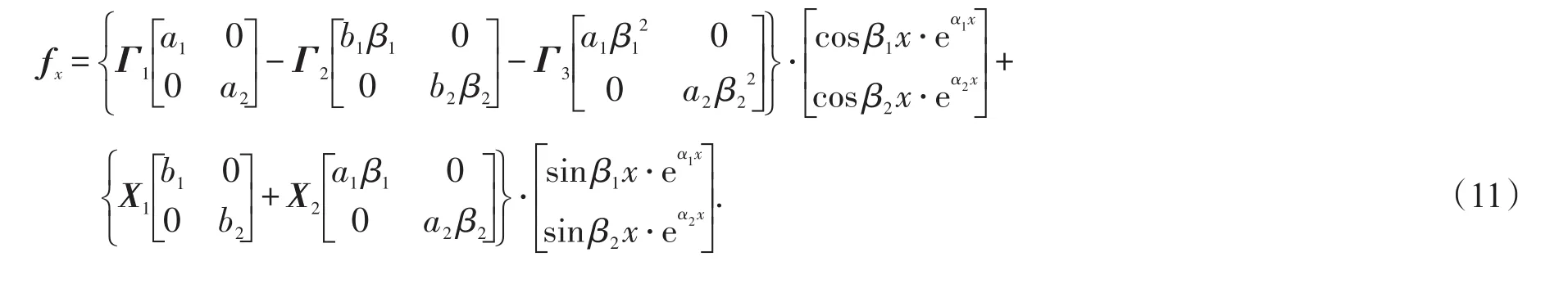
3 算例

采用本文所示方法解矩陣微分方程的特解，有

所以

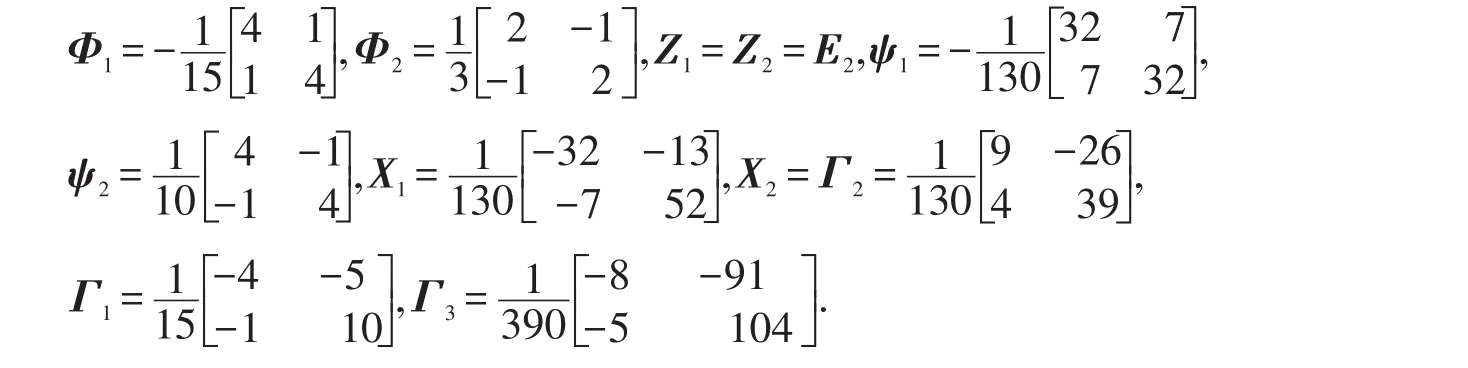
從而，矩陣微分方程（12）的1個特解為

經檢驗，式（13）確是矩陣微分方程（12）的1個特解.

4 結束語

本文在二階微分方程組研究的基礎上，根據待定矩陣法和按列比較法，得出了一類不含二階導數項的三階微分方程組的特解公式，并根據算例驗證了公式的正確性.本文結果也可通過編寫計算機程序進行計算.