高中數學立體幾何幾種高效解題方法探究

山東省壽光現代中學 李佳慶

在高中數學中，立體幾何知識屬于重點內容，也是學習的難點。因此，作為未來社會建設型人才，學生必須熟練掌握各種立體幾何解題方法與技巧，并通過大量訓練提高自身的解題質量與效率，從而促進自身更好地發展。

一、提高空間想象力

對高中數學學習而言，平面圖形認識到立體圖形認知實際上是一個飛躍，而這一飛躍需要較長過程。為了實現飛躍，一些高中同學會采取有效結合自制空間模型和數學題目的方式，并進行反復觀察；另一些高中同學則會仔細觀察并揣摩教材中的立體圖形，對立體幾何中線、角、面間的關系進行判斷，找出輔助線作法，從而確立立體空間觀念。這也就意味著在具體學習過程中，應該在綜合考慮自身實際情況的基礎上，合理選擇解題方法，并逐漸建立空間觀念，促進自身空間想象能力的提升，為后續立體幾何問題的解決奠定基礎。

在實際操作中，要想加強自身的空間感，應該采取簡單模型構建的方式來激發自身的聯想與想象。例如，可以先制作簡單的長方體與正方體，之后通過仔細觀察，明確其中線線、面面以及線面間關系，然后通過具體立體幾何問題完成拓展延伸，以此來促進自身解決問題能力的提升。同時，在了解了空間幾何線面關系后，高中生要想掌握高效、正確的解題方法，還應該培養自身的繪圖能力。這就意味著高中生應該從簡單繪圖入手，并在掌握基本技法的基礎上進行延伸，保證自身能夠以題干為依據繪制圖像，為想象與問題解決提供便利。

二、實現圖形轉換

圖形轉換也是有效解決立體幾何題目的有效方式。在解答一些立體幾何題目時，如求取值范圍、求最值等，若可以靈活變化圖形，并加強對運動變化理念的運用，那么就可以進一步分析問題，并快速解出正確答案。同時，高中生還可以通過構建輔助圖形的方式，實現原命題特殊化，降低復雜問題難度，并將不熟悉的問題轉化成常見問題。

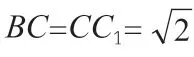
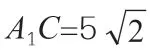
由此看來，在解答立體幾何中范圍和最小值問題時，要正確、合理地轉變圖形，并以變化觀念分析、解決問題，只有這樣，才能獲得良好的解題效果，促進自身數學素養與學習能力的提升。

三、提高邏輯論證能力

在對高中數學立體幾何知識進行學習時，還可以通過多種方式的運用，如類比平面幾何、構建模型以及聯系實際生活等，提出相應的命題或猜想。需要注意的是，在命題提出后，不能急于做出肯定或否定判斷，而是要利用特例檢驗命題，并在對命題性質進行確定后，探索相應證明方法。在實際分析過程中，要想實現由局部到整體、由低到高，就必須在具體解題過程中融入邏輯論證能力與綜合分析能力，這樣不但可以提高解題效率與正確性，還能夠鍛煉邏輯論證能力與綜合分析能力。同時還應該從不同角度分析立體幾何題目，如綜合處理距離、垂直、角以及平行等問題，只有這樣，才能促進高中生解題能力的提升，并增強其數學素養。

四、綜合運用解題技巧

在實際學習過程中，不能局限于自身思維，在對立體幾何問題進行解決時，不但要運用立體幾何知識，還應該綜合運用各種解題技巧與知識體系。這也就意味著高中生應該在解題過程中綜合運用運動距離、空間幾何以及函數等思想，并通過對各種學習技巧的利用，找出最簡的解題方法。

以線段最短問題為例：正方體ABCD—A1B1C1D1的棱長是3，其中棱AA1上有一點E，已知A1E為1，且是A1BD這一截面上不斷移動點F，求AF與FE的最小值。

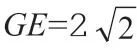
由此看來，在實際學習中，只有對思維進行發散，綜合運用各種解題技巧，才能為解決立體幾何問題提供便利，并促進自身學習效率的提高。

綜上所述，掌握立體幾何解題方法具有重要意義，熟練掌握立體幾何相關知識，并通過提高空間想象力、實現圖形轉換、提高邏輯論證能力以及綜合運用解題技巧等方式，提高解題的質量與效率，從而為后續學習奠定良好基礎。