創新題型這樣考

趙愛麗

類型一：設置“新定義”

“新定義”試題是指給出一個考生從未接觸過的新規定、新概念，要求考生現學現用，其目的是考查考生的閱讀理解能力、應變能力和創新能力，培養學生自主學習、主動探究的品質.此類型問題可能以文字的形式出現，也可能以數學符號或數學表達式的形式出現，要求考生要先準確理解“新定義”的特點，再加以靈活運用。特別提醒：“給什么，用什么”是運用“新定義”解題的基本思路。

例1.(2018 屆河南鄭州一模)如果把四個面都是直角三角形的四面體稱為“三節棍體”，那么從長方體八個頂點中任取四個頂點，則這四個頂點是“三節棍體”的四個頂點的概率為_____.

解析：從長方體ABCD-A1B1C1D1中任選四個頂點的選法有(種)，以A為其中一個頂點的四個面都是直角三角形的三棱錐有A-A1D1C1，A-A1B1C1，A-BB1C1，A-BCC1，A-DCC1，A-DD1C1，共6 個。

同理，以B，C，D，A1，B1，C1，D1為其中一個頂點的三棱錐也各有6 個，但所有列舉的三棱錐均出現2 次，所以四個面都是直角三角形的三棱錐有。

點評：本題以立體幾何知識為背景，考查古典概型概率計算公式，形式較為新穎。有利于考查考生的閱讀能力、審題能力和綜合應用能力，其求解關鍵是正確理解新定義“三節棍體”，并根據長方體的對稱性，利用列舉法求解長方體中“三節棍體”的個數。

類型二：設置“新運算”

“新運算”是指在現有的運算法則和運算律的基礎上定義的一種新的運算，是一種特別設計的計算形式，它使用一些特殊的運算符號，如“*”“?”“※”等，這些符號與四則運算中的加減乘除符號是不一樣的。“新運算”類問題的情境一般比較陌生，求解時考生需要坦然面對，先準確理解“新運算”法則，再加以靈活運用即可解決問題。特別注意：新定義的算式在沒有轉化前，是不適合運用現有的運算法則和運算律進行計算的。

例2.定義一種運算“※”，對于任意n∈N*均滿足以下運算性質：(1)2※2017=1；(2)(2n+2) ※2017=(2n)※2017+3.則2018※2017=_______.

解析：設an=(2n)※2017，則由運算性質(1)知a1=1，由運算性質(2)知an+1=an+3，即an+1-an=3.

于是，數列{an}是等差數列，且首項為1，公差為3.

故2018※2017=(2×1009)※2017=a1009=1+1008×3＝3025.

點評：注意到(2n) ※2017 與

[2(n+1)]※2017((2n+2) ※ 2017)結構相同，具體區別為前邊是“n”，后邊是“n+1”，于是，可將它們看作某一數列的相鄰兩項，從而通過“換元”將不熟悉的“新運算”問題轉化為熟悉的等差數列問題，這是求解本題的關鍵。

類型三：設置“新考查方向”

“新考查方向”試題是指試題考查的方式、方法與常規試題不同，此類試題設計新穎，注重對所學數學知識、方法的有效整合，側重考查考生的綜合運用能力。此類型問題的設置充分體現了考綱要求——對數學基礎知識的考查，注重學科的內在聯系和知識的綜合性，在知識網絡的交匯點處設計試題，使對數學基礎知識的考查達到必要的深度；對數學能力的考查，強調“以能力立意”，側重體現對知識的理解和應用，尤其是綜合和靈活的應用，以此來檢測考生將知識遷移到不同情境中的能力，從而檢測出考生的理性思維的廣度和深度以及進一步學習的潛能。

例3.已知三棱錐O-ABC，OA，OB，OC兩兩垂直，且OA=OB=，OC＝1，P是△ABC內任意一點，設OP與平面ABC所成的角為x，OP=Y，則Y關于x的函數的圖像為( )

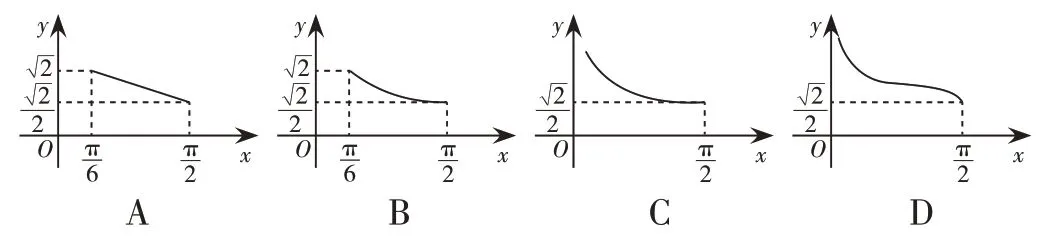
解析：設點O在平面ABC內的射影為O′，連接OO′，OP，O′P，根據等體積思想得.

因為∠OO′P=，所以OP=，即y=.易知當點P在點A或點B位置時，x取得最小值，排除選項C，D.又在上，函數y=單調遞減且其圖像為光滑曲線，所以排除選項A，選B。

點評：本題是立體幾何中線面角與函數圖像的綜合試題，形式新穎，解題的關鍵是先根據等體積思想得到函數關系式，再靈活利用函數性質排除錯誤選項。

創新型數學問題從形式上看很“新”，其提供的觀察材料和需要思考的問題異于常規試題，需要考生具有靈活、創新的思維能力，善于進行發散性、求異性思考，尋找對材料內涵的解釋和解決問題的辦法。此類問題考查的內容都在考綱要求的范圍之內，即使再新，也是在考生“力所能及”的范圍內。只要擁有扎實的數學基礎知識，以良好的心態坦然面對新情境，便可輕松破解。