仝喜峰, 陳衛松, 錢隆彥

(安徽師范大學 物理與電子信息學院,安徽 蕪湖 241000)

0 引 言

由于脈沖噪聲的沖擊特性,自適應算法在脈沖噪聲環境下的魯棒性尤為重要[1,2]。脈沖噪聲不符合高斯分布特性,信號在時域上分布著大量的尖峰脈沖(沖擊信號),其統計特性就表現為較厚的概率密度函數拖尾。針對脈沖噪聲,通常利用標準對稱穩態分布來建模[2],只有階數小于α的分數低階矩是有限的(α為特征指數,直接決定α穩態分布的概率密度函數拖尾厚度),由于不存在有界的二階矩,線性控制算法在脈沖噪聲控制中的性能顯著降低,一些非線性的濾波算法受到關注。

另一方面,由于設備的非線性特性及次級通道的非線性失真現象的存在,線性控制算法表現不佳,甚至無法收斂。為了提高線性控制算法在非線性噪聲控制中的性能,Tan L和Jiang J提出了基于Volterra級數的非線性VFxLMS算法[3,4],相比于線性FxLMS算法,VFxLMS算法可以解決算法無法收斂的問題,但降噪效果不夠好。為了保證非線性控制算法的穩定性,Leahy R等人發現脈沖噪聲存在有限的分數低階矩,提出的FxLMP算法被用于脈沖噪聲控制,具有較好的收斂效果,不足之處在于需要脈沖噪聲的先驗知識[5]。Wu L等人指出α穩態分布的脈沖噪聲的對數階矩是有限的,脈沖噪聲經過對數變換后接近于高斯分布,提出了一種基于對數變換FxlogLMS算法,該算法對脈沖噪聲更具魯棒性,并且不需要噪聲的先驗知識[6]；但該方法存在權重更新死區的缺點,因此實用性較低。最近,Lu L等人提出了一種基于Volterra擴展模型(VFxlogLMP)的非線性自適應算法[7]，VFxlogLMP算法可以有效地解決FxlogLMS算法的濾波器更新死區弊端,并可以取得更好的收斂速度和降噪效果,但算法仍然需要噪聲信號的先驗知識,并且該算法計算量相對較大。

本文采用一種S型非線性函數對誤差信號進行預處理,從而達到控制沖擊信號的目的,確保算法的穩定性,在此基礎上將變步長算法思想引入到非線性濾波算法中。仿真分析結果表明,該算法在不需要噪聲先驗知識的情況下,實現對脈沖噪聲的控制,且不存在濾波器權值更新死區。

1 自適應Volterra濾波理論基礎

Volterra濾波器可以很好地模擬非線性系統,對于各種高階內核或脈沖響應,其輸出仍然為線性。通過使用Volterra級數擴展,自適應非線性控制器的輸出y(n)表示為

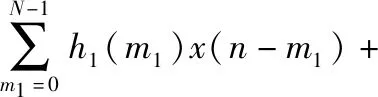
(1)

式中N為自適應Volterra濾波器的存儲長度,hr(m1,…,mr),r=1,…,R為濾波器的第r階核,這里選用二階Volterra非線性濾波器,其輸入信號可表示為

X(n)=[x(n),x(n-1),…,x(n-N+1),

x2(n),…,x2(n-N+1)]T

(2)

濾波器的權重矢量為

W(n)=[h1(n),…,h1(N-1),h2(0,0),…,

h2(N-1,N-1)]T

=[w1(n),w2(n),…,wN-1(n)]T

(3)

式中d(n)為期望信號,濾波器的輸出和誤差信號分別為

y(n)=XT(n)W(n),e(n)=d(n)-y(n)

(4)

Wu基于α穩沖噪聲的對數階矩有限,提出了FxlogLMS算法,濾波器的系數更新規則為[6]

(5)

為了克服FxlogLMS算法存在濾波器更新死區的弊端,Lu提出了基于Volterra級數的VFxlogLMP算法。修改之后的濾波器系數更新方程[7]

(6)

2 一種改進的Volterra自適應濾波方法

FxlogLMS算法和VFxlogLMP算法分別依據脈沖信號具有有限分數低階矩和對數階矩,控制了較大幅值的誤差信號對自適應濾波器權值更新的影響。上述兩種算法均可以用一般表達式表示為

W(n+1)=W(n)-μg(n)x′(n)

(7)

式中g(n)為與誤差信號e(n)相關的權值更新函數。

S型激活函數是一個非線性連續函數,函數曲線形如“S”,其中S型激活函數的表達式為

(8)

式中S(x)為一單調奇對稱的有界函數,本文將S型激活函數的單調有界特性引入到脈沖噪聲控制算法中,定義代價函數為

(9)

因此,VFxBSLMS算法的權重矢量的更新表達式為

(10)

式中μ為步長因子,β為非線性壓縮系數,且μ>0,β>0圖1為不同β值下的非線性壓縮函數曲線,從圖中可以看出隨著e(n)增大,g(n)值逐漸減小,這保障了在較大幅值e(n)下算法的穩定。β越大,g(n)對誤差信號的壓縮越劇烈。但β值選取并不是越大越好,對e(n)的過度壓縮有可能會降低算法的收斂速度。

二階Volterra濾波器的線性部分權值及二次項部分權值分別用wi(n)和wi,j(n)表示。Volterra濾波器非線性項將穩定分布的尖峰特性放大,導致輸入信號的自相關矩陣特征值擴展變大,使輸入信號相關性很強。為克服輸入信號的強相關性以及固定步長對算法收斂帶來的影響,本文采用基于Sigmoid函數[9]的變步長算法,其變步長公式為

μ1=μ2=σ[1/(1+exp(-λ|e(n)|))-0.5]

(11)

式中μ1(n),μ2(n)為基于Sigmoid函數的線性項和二次項的變步長因子。

考慮到誤差信號中仍然存在大量的沖擊信號,為了進一步地降低強脈沖信號對濾波器權值更新穩定性的影響,本文增加誤差信號預處理環節。考慮到算法的適用性,在預處理函數的設置上體現出“動態”變化的特性。定義信號預處理函數表達式為

(12)

式中c(i)為誤差信號的在線統計平均,i為信號樣本數。

3 算法仿真與性能分析

以圖2所示的FIR系統辨識模型為例,對本文算法進行仿真和性能分析[10]。

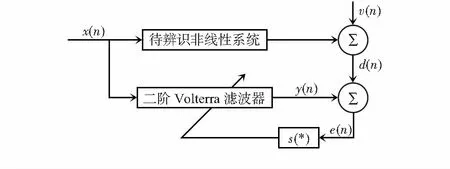
圖2 系統辨識原理框圖

設非線性系統是一個記憶長度N=3的二階Volterra濾波系統,二階非線性系統的期望信號為

d(n)=-0.76x-x1+x2+0.5x2+2·x·x2-

(13)

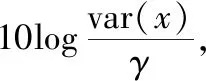
由于脈沖噪聲的二階矩不存在,因此利用平均殘余誤差ANR(Averaged Noise Reduction)來進行性能比較[11],其定義為

(14)

選取FxlogLMS、VFxlogLMP算進行比較,每種算法的最優步長通過實驗的方式進行確定。圖3為三種算法在脈沖噪聲強度分別為α=1.2(圖3(a)),α=1.5(圖3(b)),α=1.8(圖3(c))的環境下的降噪性能比較。

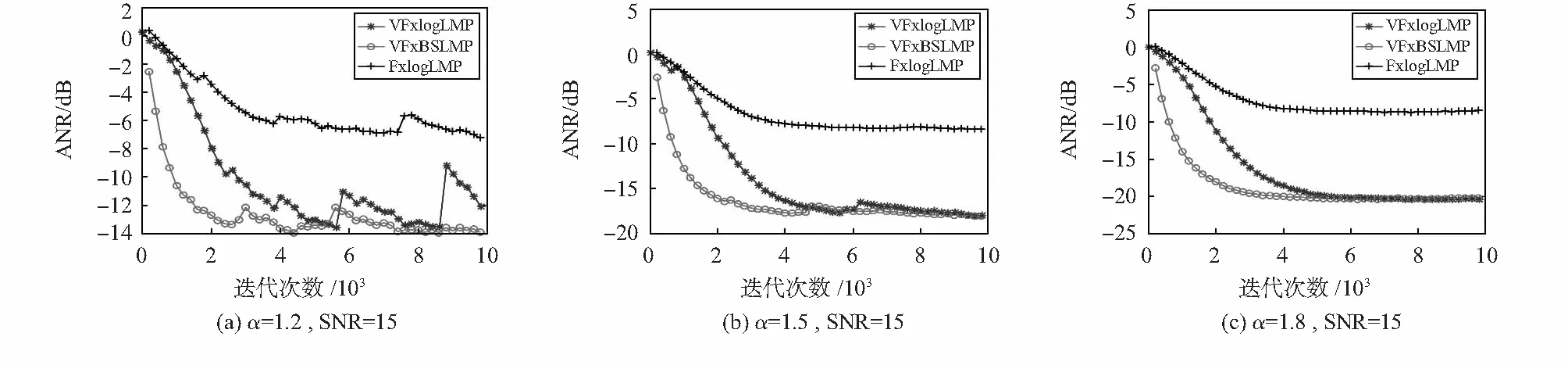
圖3 三種算法的平均殘余誤差ANR對比

從圖3(a)可見,當α=1.2(較強脈沖噪聲背景)時,FxlogLMS算法相比較其他兩種算法,平均殘余誤差的絕對值要小5～8 dB；VFxlogLMP算法和VFxBSLMS算法都可以取得比較理想的降噪效果,但VFxBSLMS算法在迭代2 500次左右就已經達到了收斂狀態,而VFxlogLMP算法則要到4 800次才能完成,前者收斂速度明顯較優。由于脈沖強度太大,三種算法在迭代過程中都不同程度上受到較高脈沖樣本的干擾。由圖3(b)和圖3(c)可見,當α=1.5及α=1.8(脈沖強度較弱)時,三種算法對較弱的脈沖噪聲環境都可以表現很好的魯棒性。從不同噪聲環境下三種算法的表現上來看,VFxBSLMS算法在算法收斂速度以及降噪效果上均優于FxlogLMS算法,在降噪效果上VFxBSLMS算法和VFxlogLMP算法都可以達到最高20 dB的降噪量,但收斂速度上VFxBSLMS算法仍然優于VFxlogLMP算法。

使用權系數誤差范數對算法性能進行進一步的分析,所有仿真曲線都是通過20次獨立仿真結果取平均得到

(15)

圖4(a)是VFxlogLMP和VFxBSLMS算法在α=1.2時的權系數誤差范數對比圖,兩種算法的誤差曲線均可收斂到-20 dB,但在收斂速度上本文算法要遠快于VFxlogLMP算法。

由圖4(b)可以看出VFxBSLMS算法線性核誤差(h1)及非線性核誤差(h2)幾乎同時在迭代450次左右達到收斂,而VFxlogLMP算法的線性核非線性核誤差則要到1 600次才能達到收斂狀態。兩種算法的線性核誤差值均小于二階項核誤差值,這是因為Volterra級數二階項相關矩陣的特征值大于線性項。由于在圖3(a),(c)已經表明FxlogLMS算法在收斂效果上低于VFxBSLMS及VFxlogLMP算法,本文不再對其進行權系數誤差范數以及Volterra濾波器核誤差的對比分析。

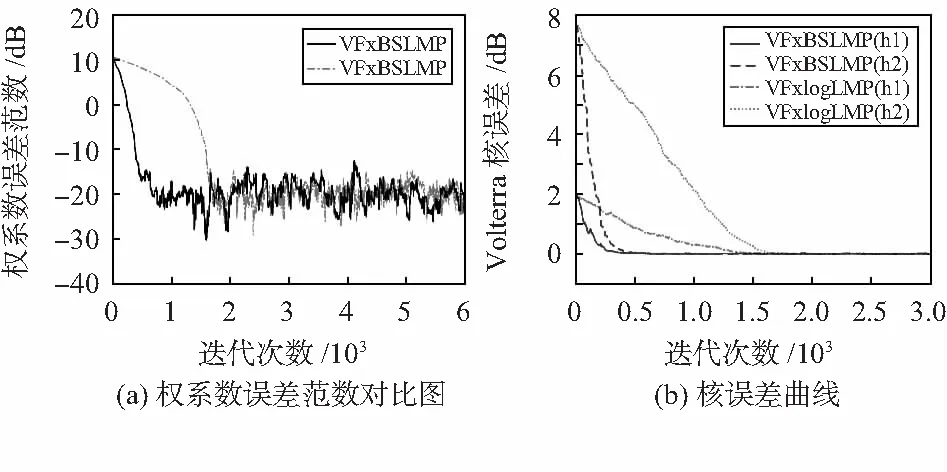
圖4 α=1.2時算法性能比較

從圖5(a)可以看出,當脈沖噪聲強度較大(α=1.5)時,在迭代500次后,VFxBSLMS算法的噪聲幅值穩定在6 dB以內,當迭代超過1 500次后穩定在2 dB內。而其他兩種算法則在3～20 dB之間。當脈沖強度較小(α=1.8)時,在噪聲衰減量上,VFxBSLMS算法的優勢已經并不夠明顯,其主要原因是α=1.8時的噪聲已經接近于高斯分布。在收斂速度上,本文算法噪聲在迭代500次左右便呈現濾波完成狀態,而其他兩種算法則分別需要迭代1 300次和2 000次才能完成脈沖噪聲濾波。

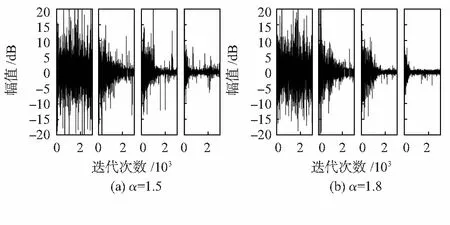
圖5 不同算法的濾波效果對比

(從左至右分別為噪聲信號、FxlogLMS算法、VFxlogLMP算法、VFxBSLMS算法)

4 結 論

仿真實驗表明:本文算法構成的Volterra濾波器可以獲得較快的收斂速度,并且不需要噪聲信號的先驗知識,適用環境較為靈活。由于本文引入變步長算法思想來進行步長更新,雖然提高了算法的收斂速度,一定程度上提高了算法的計算量負載,在進一步的研究中仍需不斷改進,進一步減小計算量。