單箱連續(xù)剛構(gòu)靜載試驗分析方法對比研究

汪賢安

（山西省交通科技研發(fā)有限公司，山西 太原 030032）

0 引言

為保證橋梁的使用安全，對其承載能力的鑒定是一個重要內(nèi)容，連續(xù)剛構(gòu)作為一種常見的大跨徑預應力混凝土梁橋，其施工方便、跨越能力強、施工技術(shù)成熟，且外形也較為美觀，使用眾多，但是常規(guī)的桿系結(jié)構(gòu)有限元分析方法無法精準地分析其橫向受力情況，而實際工程中橫橋向受力分析是重要的組成部分，梁格法與修正的單梁模型法可以有效地解決這一問題，本文采用大型有限元分析軟件Midas Civil就單梁法、修正的單梁模型法和梁格法3種方法對連續(xù)剛構(gòu)橋進行分析討論[1]。

1 工程概況

本文以一座跨徑（73.32+3×135+73.32）m的預應力混凝土連續(xù)剛構(gòu)橋進行分析，該橋上部結(jié)構(gòu)采用單箱單室截面；下部采用雙薄壁空心墩，墩臺基礎(chǔ)采用灌注樁基礎(chǔ)。設計荷載為公路-Ⅰ級；橋面凈寬為凈-2×11.75 m；地震動峰值加速度為0.15g。

該橋箱梁截面形式為單箱單室，頂板寬12.75 m，底板寬7 m，翼緣板懸臂長為2.875 m，截面高度由2.8 m漸變到8.5 m，截面如圖1所示。

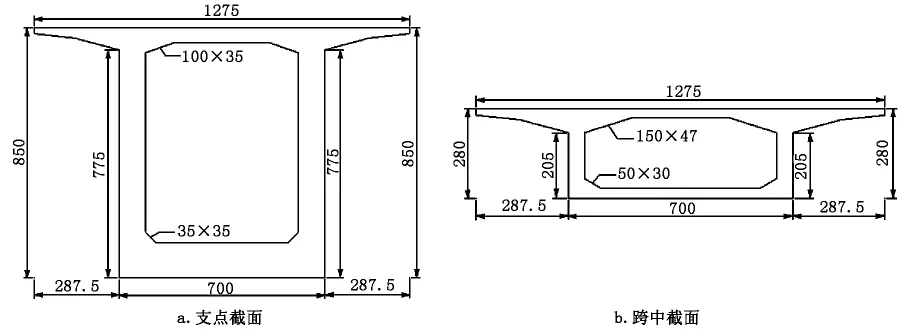
圖1 截面形式（單位：cm）

2 結(jié)構(gòu)分析原理

2.1 單梁法與修正的單梁模型法

單梁法是將梁體作為一根整體的單梁進行離散分析，無法考慮橫向分布的影響，修正的單梁模型法是根據(jù)一些工程的內(nèi)力分析，當箱梁的截面因畸變引起的扭曲應力很小時，活載引起的約束扭轉(zhuǎn)正應力一般不超過活載彎曲正應力的15%，在計算箱型截面某個點的正應力時可以忽略箱梁的畸變效應，只考慮箱梁的縱向撓曲及約束扭轉(zhuǎn)效應，在各肋板平均承受外荷載的基礎(chǔ)上，把邊肋所受的荷載最大增大15%，即偏載系數(shù)最大不超過1.15[2]，對于偏心距離的差異性沒有描述，本文在單梁模型值的基礎(chǔ)上乘以1.15系數(shù)作為不對稱加載時偏載側(cè)的結(jié)果，對應乘以0.85的系數(shù)作為非偏載側(cè)的結(jié)果。該方法操作簡單，內(nèi)力的橫向分布簡單地按線性變化考慮，對于簡單的箱型截面是可以的，但對于復雜的異型結(jié)構(gòu)無能為力，特別是對于荷載偏心距與偏載系數(shù)取值之間的相關(guān)性并無明確規(guī)定。

2.2 梁格法

梁格法將橋梁上部結(jié)構(gòu)模擬為若干個等效梁格，把分散在梁每一區(qū)段內(nèi)的彎曲剛度和抗扭剛度集中在臨近的等效梁格上，實際的縱向剛度與橫向剛度集中于對應的縱橫向梁格內(nèi)[3]。在相同的外荷載作用下，任意一梁格內(nèi)的內(nèi)力應等于該梁格所代表的實際結(jié)構(gòu)部分的單元內(nèi)力，且變形與原結(jié)構(gòu)相同。

3 梁格截面特性計算及計算模型[4]

3.1 截面特性計算

縱向構(gòu)件抗彎剛度：EIy，其中Iy表示構(gòu)件表面積對y軸的慣性矩；

縱向格構(gòu)剪切剛度：GAs，其中As表示梁格代表的縱梁肋板面積；

縱向格構(gòu)扭轉(zhuǎn)剛度：GJx，其中Jx表示縱梁抗扭慣性矩與板抗扭慣性矩之和；

橫向梁格剛度：

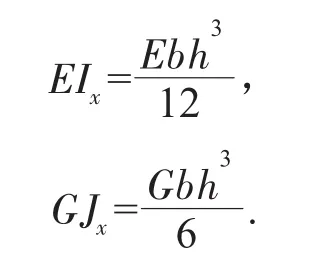
梁格劃分基本原則應確保等效后結(jié)構(gòu)的傳力途徑、作用方式、相對剛度不變。

3.2 結(jié)構(gòu)離散模型

a）單梁模型采用平面桿件有限元法，根據(jù)橋梁的結(jié)構(gòu)型式，采用Midas Civil對橋梁進行建模，將上部作為一根梁來考慮，有限元模型離散為361個節(jié)點，352個單元；模型結(jié)構(gòu)如圖2所示。

圖2 單梁模型

b）梁格模型采用Midas Civil進行建模，本橋劃分為2根縱梁，劃分縱梁時沿箱梁截面中心線劃分，以左右腹板為中心建立縱梁單元，橫梁分為實際橫梁和虛擬橫梁兩種，實際橫梁依據(jù)實際橫梁剛度建立單元，虛擬橫梁采用工字型截面，頂、底板厚度按對應箱梁頂?shù)住搴穸热　Ｓ嬎隳Ｐ鸵妶D3。

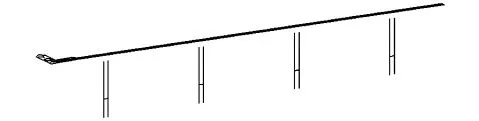
圖3 梁格劃分模型

4 分析工況

本文主要結(jié)合荷載試驗對比3種方法在相同工況下產(chǎn)生的內(nèi)力、變形，主要考慮車輛荷載，選取相鄰的兩跨來進行試驗，根據(jù)需要設計以下幾個工況：工況1：第6跨（邊跨）最大正彎矩工況（偏載）；工況2：第6跨最大正彎矩工況（正載）；工況3：第7跨跨中最大正彎矩工況（偏載）；工況4：第7跨跨中最大正彎矩工況（正載）。

本次試驗內(nèi)力采用在箱梁內(nèi)部粘貼應變傳感器的方式采集，分別在第6、第7跨彎矩最大截面處設置測試截面；撓度采用精密水準儀測量。具體應變、撓度布置如圖4，圖4中“-”表示應變測點，“”表示撓度測點。

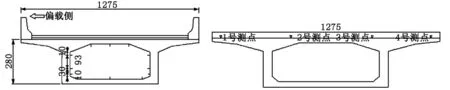
圖4 測點布置

5 模型結(jié)果與實際數(shù)據(jù)對比

5.1 應力對比分析

判斷橋梁承載能力的重要要素之一就是橋梁在外荷載作用下的應力變化規(guī)律，因此，需要通過對3種方法所得結(jié)果與實際值進行對比。通過工況1～工況4分別對第6跨和第7跨加載，計算出單梁模型值與梁格模型值，在單梁模型計算結(jié)果的基礎(chǔ)上，對其進行修正，偏載側(cè)乘以1.15的系數(shù)，非偏載側(cè)乘以0.85的系數(shù)，得出修正的單梁模型值，3種方法所得理論值結(jié)合實測值繪制如圖5所示，圖中負值 表示拉應力。

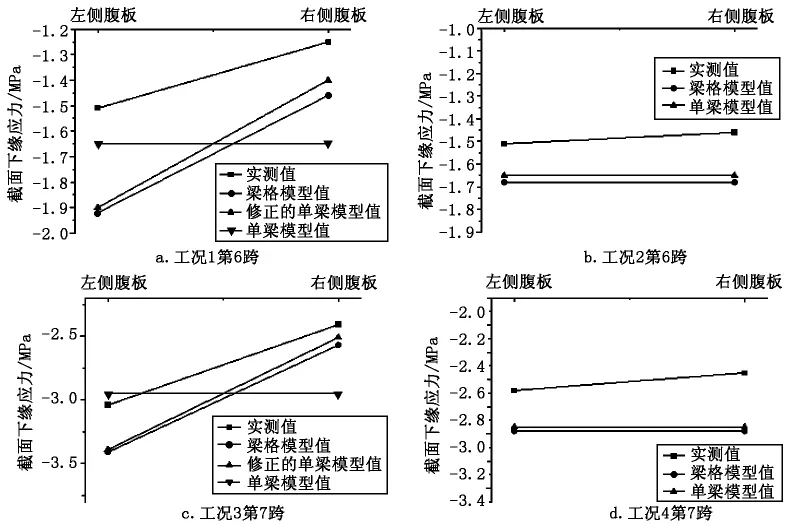
圖5 測試截面應力值

通過圖5可以看出，現(xiàn)場實測值均小于梁格模型與修正的單梁模型理論值，且梁格法與修正單梁模型法理論值相對誤差較小，在變化趨勢也基本相似，而單梁模型在對稱加載情況下與梁格法極為接近，但無法考慮結(jié)構(gòu)內(nèi)力的橫向分布情況，在做偏載工況時從單梁模型直接提取的計算值無法使用，需要加以修正后才能進行對比分析。

5.2 撓度對比分析

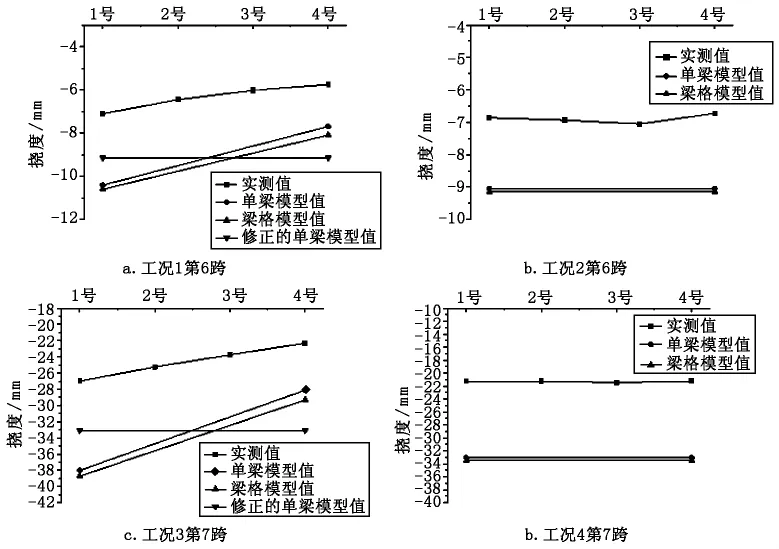
圖6 測試截面撓度值

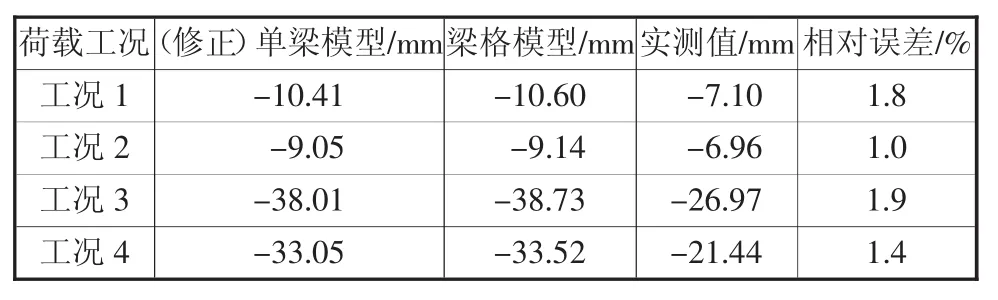
表1 各工況下最大撓度對比匯總

對比兩種模型相同工況下的撓度值，由表1可以看出：

a）分析工況1，第6跨跨中截面在偏載作用下修正的單梁模型最大豎向撓度理論值為10.41 mm，梁格模型最大豎向撓度理論值為10.60 mm，實測值為7.1 mm。

b）分析工況2，第6跨跨中截面在正載作用下單梁模型最大豎向撓度理論值為9.05 mm，梁格模型最大豎向撓度理論值為9.14 mm，實測值為6.96 mm。

c）分析工況3，第7跨跨中截面在偏載作用下修正的單梁模型最大豎向撓度理論值為38.01 mm，梁格模型最大豎向撓度理論值為38.73 mm，實測值為26.97 mm。

d）分析工況4，第7跨跨中截面在正載作用下單梁模型最大豎向撓度值為33.05 mm，梁格模型最大豎向值為33.52 mm，實測值為21.44 mm；總體而言，兩種模型理論值均大于實測值，二者之間相對誤差較小，在2%以內(nèi)。

通過與應力圖相同的方式繪制出3種方法所得理論值與實測撓度值的對比圖，見圖6，由圖6可以看出，工況1～工況4作用下實測值均小于3種方法理論值，且梁格模型值與修正的單梁模型值變化趨勢基本相同，與正載作用下的單梁模型值也基本一致。梁格法和修正的單梁模型法可以較好地反映結(jié)構(gòu)實際變形情況，而單梁模型直接得出的結(jié)果無法反映偏載工況下的結(jié)構(gòu)變形情況。

6 結(jié)語

a）單梁模型對于對稱加載結(jié)構(gòu)理論計算值尚可，但對于偏載工況無法考慮，需要對結(jié)果進行修正。

b）修正單梁模型法與梁格法計算結(jié)果對于單箱單室結(jié)構(gòu)較為接近，均可較好地滿足本例結(jié)構(gòu)類型的使用要求，在今后類似的工程中可選擇這兩種方式進行分析。