艦載捷聯慣導系統的航行中快速在線標定

袁 鵬，楊 雨，陳 光，晏 亮，武雨霞

（北京航天時代激光導航技術有限責任公司，北京100094）

0 引言

由于捷聯慣導系統直接固連在載體上,直接測量載體的角運動和線運動,因此若零偏和標度因數誤差沒有被準確標定出來,則會造成較大的誤差。目前,針對靜基座情況的標定技術已經較為成熟[1-4]。針對處于系泊狀態的捷聯慣導系統的標定,國內外學者提出了采用GPS提供實時精確位置信息、以位置誤差作為量測量、基于Kalman濾波器的系統級標定方法[5-6],以實現捷聯慣導系統的在艦免拆卸標定。隨著慣性技術的不斷發展,出現了艦載捷聯慣導系統在航行中對快速標定的新需求。

本文的標定全過程可分為3個步驟：粗對準、精對準、標定。粗對準過程采用了基座慣性系粗對準方法[7]。考慮到速度匹配方法受船體變形影響非常小[8],本文采用了速度匹配Kalman濾波進行精對準。標定則采用了速度加位置匹配Kalman濾波。通過簡化陀螺和加速度計的輸出誤差模型來對Kalman濾波器進行降維,大幅縮短了標定時間。通過慣導系統的雙軸旋轉機構實現各標定轉位,艦船在航行中僅需保持勻速直航狀態,即可充分激勵各標定參數。該方法在工程上易于實現,標定時間短,操作簡單,能夠大幅降低成本。

1 慣性器件誤差模型與Kalman濾波器模型

由于安裝誤差的長期穩定性很好,因此可將安裝誤差視作常值,事先裝訂進捷聯慣導系統中,進而簡化陀螺和加速度計的誤差模型,降低Kalman濾波器的維數。

陀螺誤差模型的表達式為

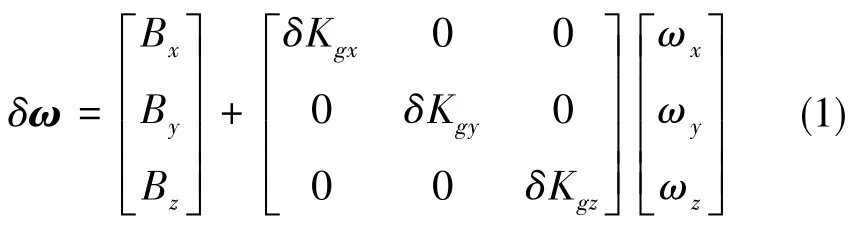
式（1）中,Bx、By、Bz為陀螺零偏,δKgx、δKgy、δKgz為陀螺標度因數誤差,ωx、ωy、ωz為陀螺測得的角速度。

加速度計誤差模型的表達式為

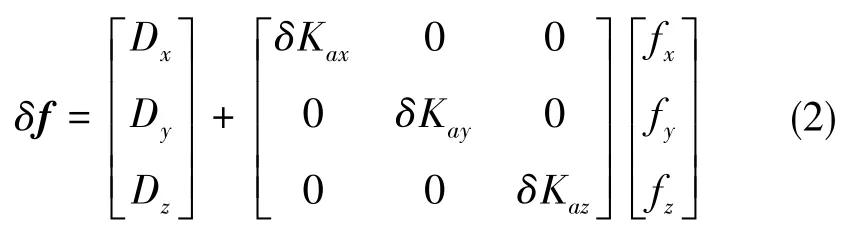
式（2）中,Dx、Dy、Dz為加速度計零偏,δKax、δKay、δKaz為加速度計標度因數誤差,fx、fy、fz為加速度計測得的比力。

由于可將安裝誤差視作常值處理,根據上述模型,Kalman濾波器的狀態變量能夠減少12個。狀態變量選取如下,共24維

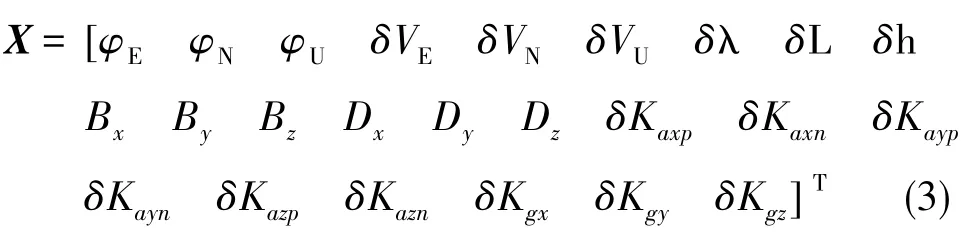
式（3）中,φE、φN、φU為慣導的東北天失準角,δVE、δVN、δVU為慣導的東北天速度誤差,δλ、δL、δh為慣導的經度誤差、緯度誤差、高度誤差,δKaxp、δKayp、δKazp為加速度計正向標度因數誤差,δKaxn、=δKayn、δKazn為加速度計負向標度因數誤差。

狀態方程為

式（4）中,

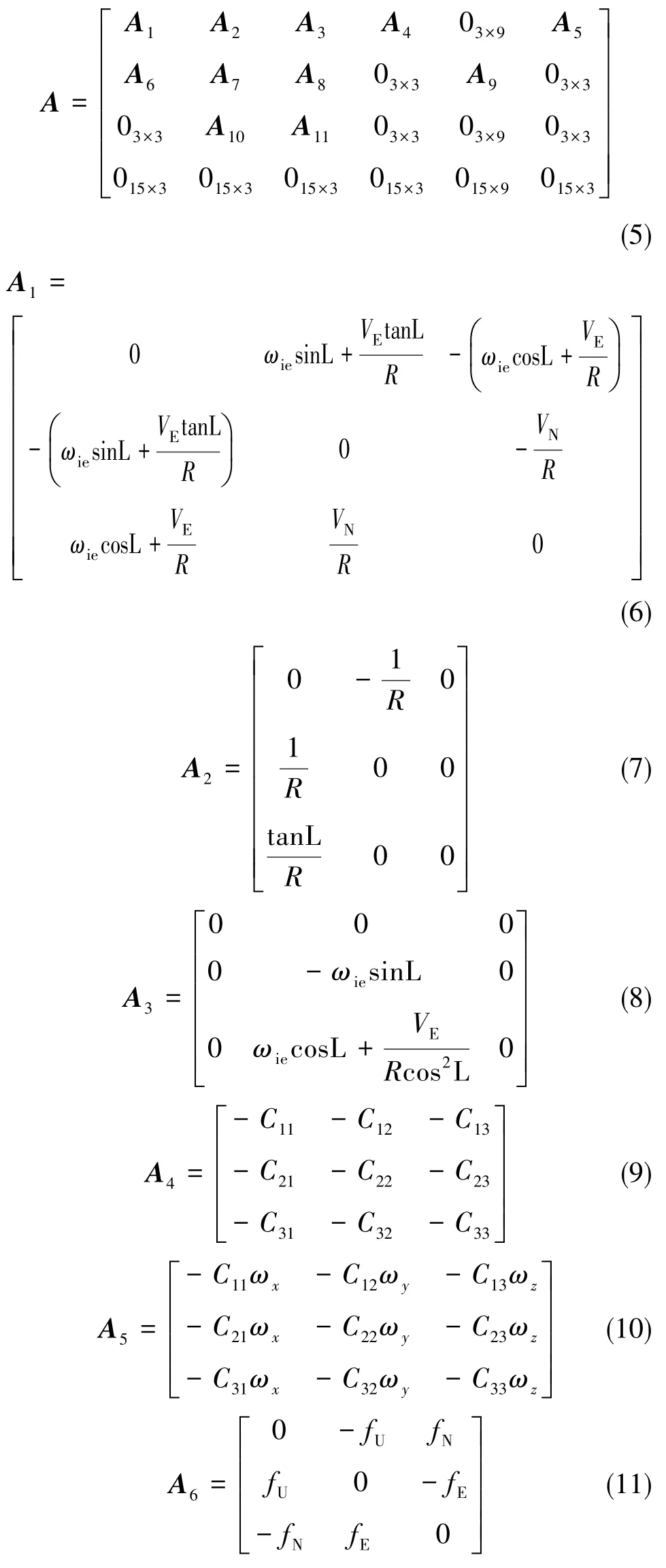
其中,R為地球半徑,ωie為地球自轉角速率,VE、VN、VU為慣導的東北天向速度,fE、fN、fU為加速度計的東北天向加速度,C11、C12、C13、C21、C22、C23、C31、C32、C33為姿態矩陣對應位置上的元素,w1、w2、w3、w4、w5、w6為零均值隨機白噪聲。

量測方程為

式（18）中,

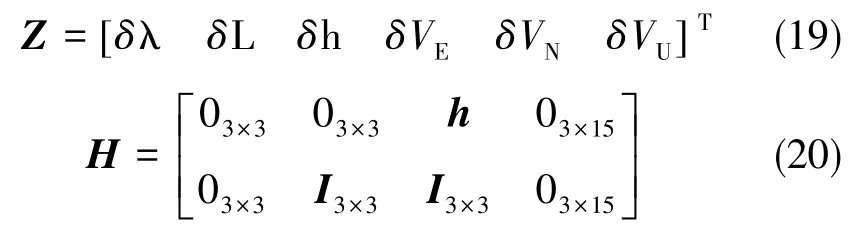
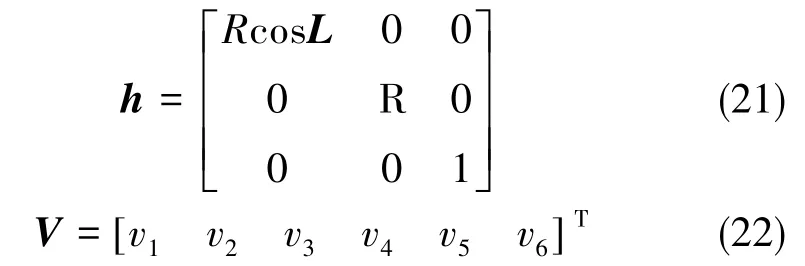
其中,I3×3為單位矩陣,v1、v2、v3、v4、v5、v6為零均值隨機白噪聲。

2 標定路徑編排方案

傳統捷聯慣導系統不具備雙軸旋轉機構,同時艦船無法像飛機一樣做出各種機動動作來激勵所有待標定參數。因此,為了激勵待標定參數,本文采用了具備雙軸旋轉機構的捷聯慣導系統,通過IMU自身改變姿態來激勵待標定參數。通過可觀測性和可觀測度分析[9-10]設計了一種標定路徑編排方案,下面直接給出標定路徑編排方案,如表1所示。

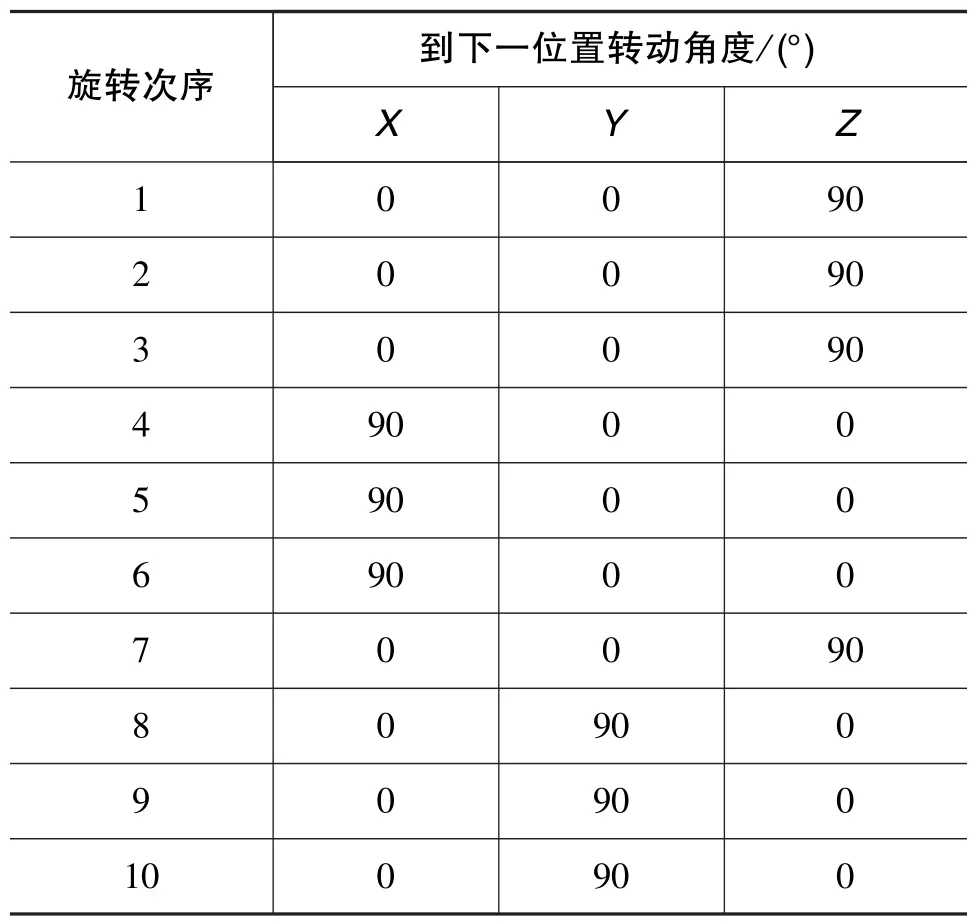
表1 標定路徑編排Table 1 Calibration procedure

3 仿真試驗驗證

本文仿真條件為：

（1）艦船直線航行的速度模型

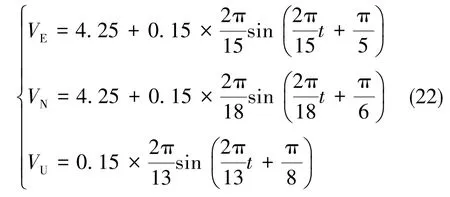
為VE、VN、VU分別加上大小為0.005m/s的隨機噪聲,作為GPS輸出的實時速度信息。

（2）艦船搖擺模型

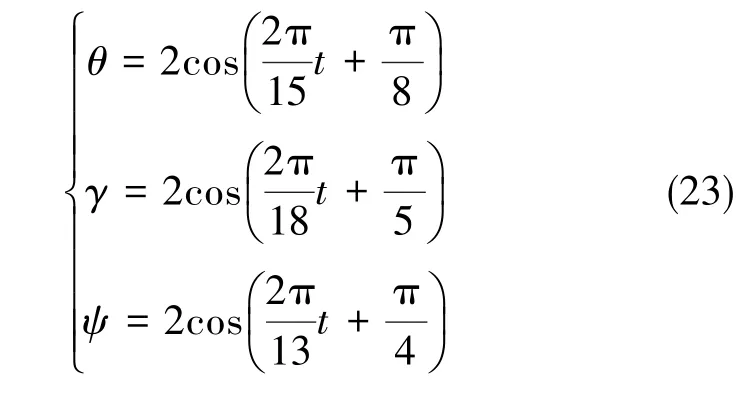
式（23）中,θ為縱搖角,γ為橫搖角,ψ為艏向角。

（3）仿真標定時間為1800s

根據搖擺模型和設計的標定路徑編排,使用C語言程序生成標定過程中的加速度計和陀螺輸出,并進行了標定仿真試驗。在試驗過程中,根據標定精度要求,對保存的標定數據進行迭代計算,可以提高標定精度[11-12]。本文進行了4次標定仿真試驗,取4次標定估計結果的均值作為最終標定結果,仿真結果如表2所示。

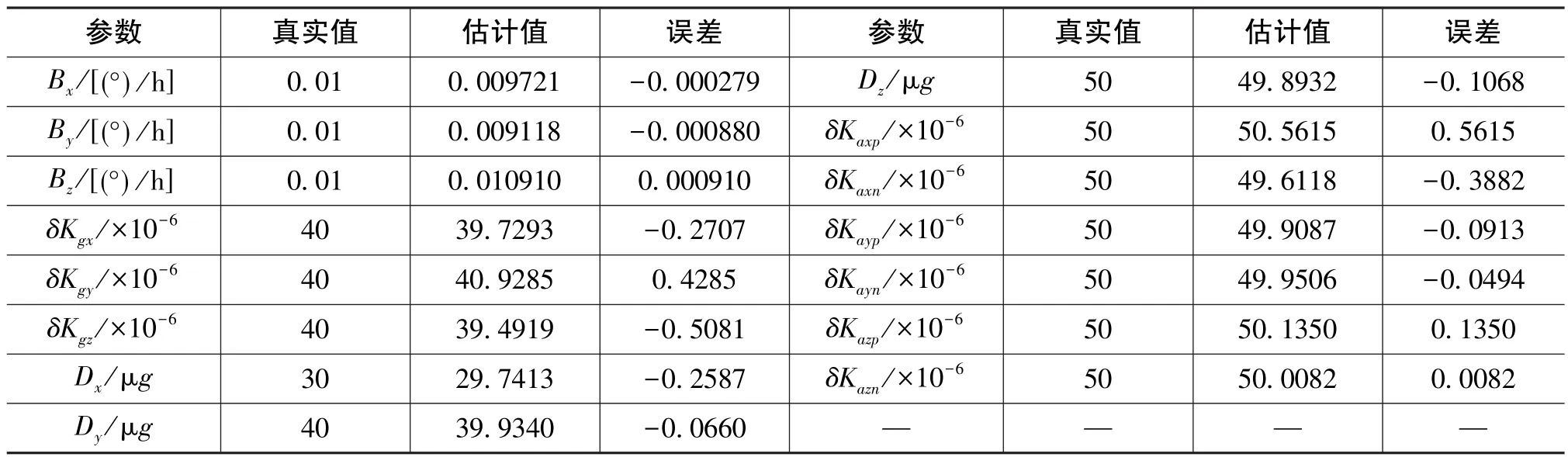
表2 仿真標定參數真實值和估計值比較Table 2 Comparison of calibration results of the true and estimated error parameters

由表2可以看出,加速度計零偏估計精度優于1μg,陀螺零偏估計精度優于0.001（°）/h,加速度計標度因數誤差和陀螺標度因數誤差估計精度均優于 1×10-6。

下面給出4次標定仿真試驗中某次試驗的陀螺和加速度計經過多次迭代修正后的零偏仿真估計曲線,如圖1所示。由圖1可知,陀螺和加速度計的零偏經過多次迭代修正后,估計曲線均趨于0,這表明陀螺和加速度計的零偏最終成功逼近了真值。

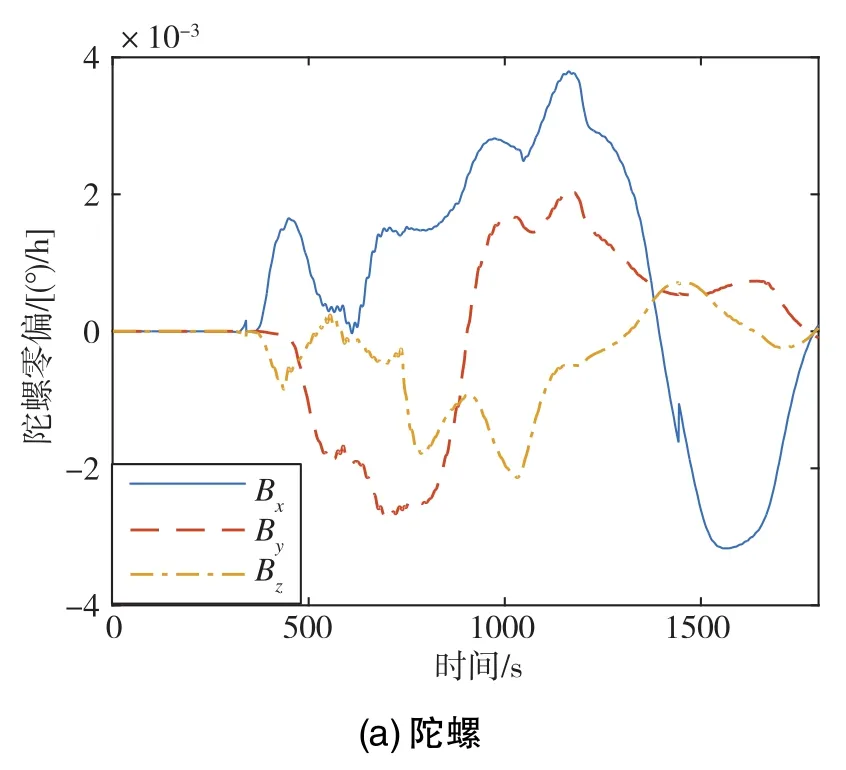
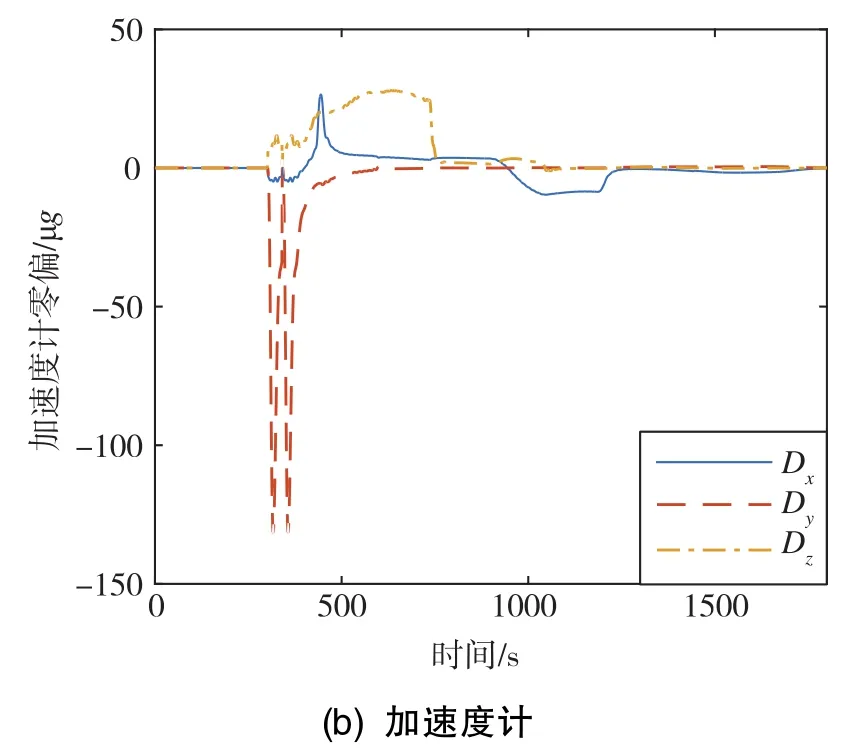
圖1 陀螺和加速度計零偏仿真估計曲線Fig.1 Simulation estimation curves of gyro and accelerometer bias

4 跑車模擬航行中標定試驗驗證

采用某型帶雙軸旋轉機構的激光慣組進行跑車模擬航行中標定試驗,標定時間為1800s。目前,不依賴于高精度轉臺的靜基座系統級標定技術已經能夠實現很高的標定精度,本文選擇以此方法作為參考,連續做出4組靜基座標定試驗,取4次標定結果的均值作為靜基座的最終標定結果,再連續做出4次跑車模擬航行中標定試驗,取4次標定結果的均值作為動基座的最終標定結果。以靜基座標定結果作為參考,對跑車模擬航行中標定試驗結果進行評價,試驗結果如表3所示。

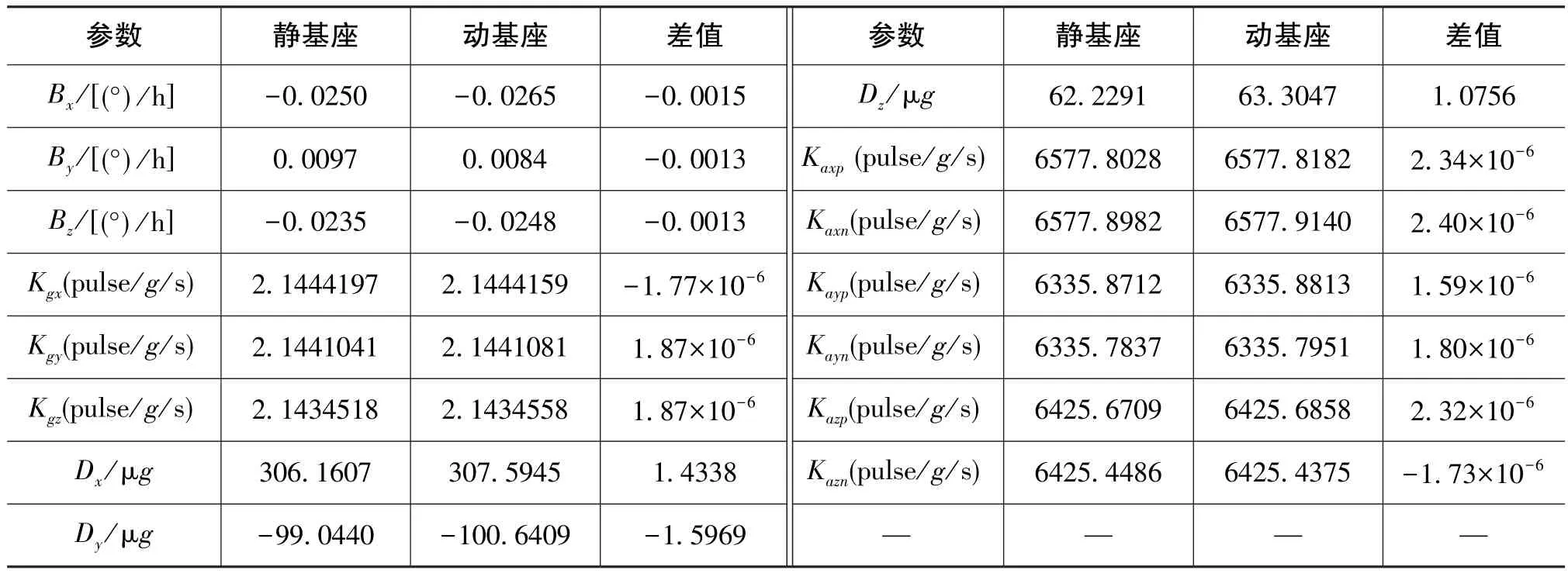
表3 捷聯慣導動基座標定結果和靜基座標定結果比較Table 3 Comparison of calibration results of SINS on moving-base and SINS on stationary base

由表3可知,本文介紹的航行中標定方法的標定結果與靜基座系統級標定方法的標定結果相比,陀螺標度因數相差小于2×10-6,加速度計標度因數相差小于2.5×10-6,陀螺零偏相差小于0.002（°）/h, 加速度計零偏相差小于2μg。

這里給出4次跑車試驗中某次標定試驗實際系統的陀螺和加速度計經過多次迭代修正后的零偏估計曲線,如圖2所示。由圖2可知,陀螺和加速度計的零偏經過多次迭代修正后,估計曲線均趨于0,這表明陀螺和加速度計的零偏最終成功逼近了真值。

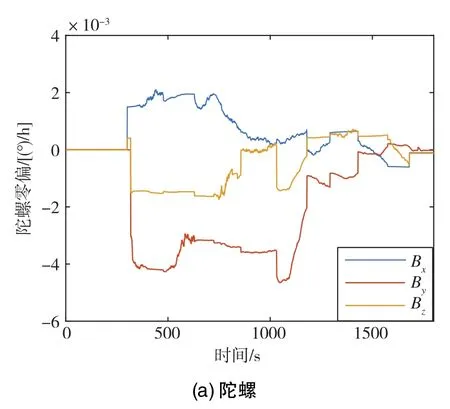
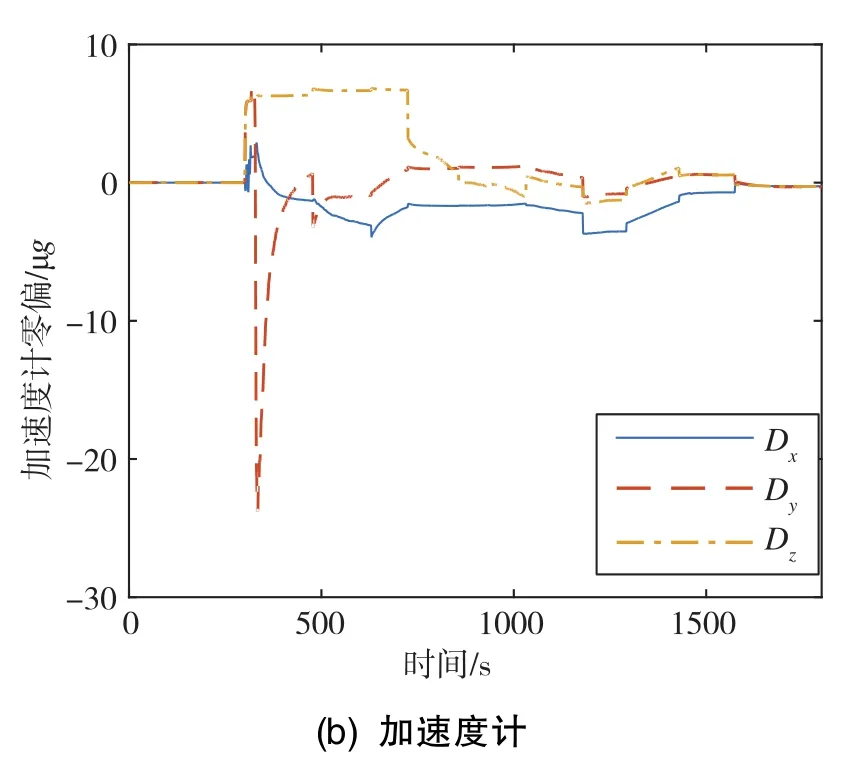
圖2 實際系統的陀螺和加速度計零偏估計曲線Fig.2 Estimation curves of actual SINS gyro and accelerometer bias

5 結論

本文提出了一種基于Kalman濾波器的適用于艦載捷聯慣導系統的航行中快速在線標定方法。通過將具有良好長期穩定性的安裝誤差視作常值,并將其事先裝訂進慣導系統,降低了Kalman濾波器的維數。采取速度加位置匹配方法,利用GPS的實時速度、位置信息與捷聯慣導輸出的速度、