平流層飛艇升降階段BPNN慣性導航算法
李保國,李淑影,王 娜,張 博
(北京航空航天大學,北京100191)
0 引言
由于具備航行時間長、地面覆蓋范圍廣、相對衛星成本顯著降低等優點,平流層飛艇成為了戰略各國研究的熱點。相應地,針對其導航系統的研究也受到了越來越多的關注[1]。由于全球定位系統(Global Position System,GPS)具有定位精度高、誤差不隨時間累積的特點,很多導航系統利用GPS提供高精度位置信息。但是,GPS也存在一定缺陷,如自主性差、易受干擾等[2]。作為一種自主性導航系統,慣性導航系統(Inertial Navigation System,INS)在不需要任何外部輔助信息的前提下即可得到載體位置、速度和姿態信息[3]。但是,慣性導航系統的誤差會隨時間累積,不能長時間單獨工作。因此,飛艇導航系統多采用慣性導航/全球定位系統(INS/GPS)組合導航方式[4]。
軟式平流層飛艇在上升和下降階段呈堆疊狀態,GPS信號會被艇體間歇性遮擋,因而只能采用慣性導航,而慣性導航的誤差隨時間累積,不能持續提供高精度的導航信息。因此,必須研究新型算法,對慣性導航結果進行修正。
人工神經網絡能夠建立輸入輸出的非線性映射關系,常用來解決GPS失鎖問題。崔留爭等人研究了一種將徑向基網絡與時間序列分析進行結合的新方法,可預測Kalman濾波器的量測信息,但該方法存在INS誤差被過大估計的風險[5]。林雪原等人將陀螺和加速度計的輸出信息作為神經網絡的輸入信息,將位置和速度信息作為神經網絡的輸出信息。這種輸入輸出模型雖然具有較強的非線性映射關系,但神經網絡需要學習慣性導航的解算過程,這導致了神經網絡的復雜和不易收斂[6]。
鑒于此,本文提出了一種改進的反向傳播神經網絡(Back Propagation Neural Network,BPNN)慣性導航算法。當GPS信號有效時,基于Kalman濾波的組合導航結果將成為訓練數據,并對BPNN進行訓練;當GPS信號失效時,訓練好的BPNN則進行狀態估計,可為慣性導航提供位置、速度補償信息,有效地減緩導航誤差發散,持續提供可靠的導航結果。
1 組合導航系統結構
本文提出將基于神經網絡的人工智能方法應用于飛艇的INS/GPS組合導航系統,該方法能夠在GPS失效時間不超過30s的情況下提供滿足精度要求的位置和速度信息。在正常工作時,GPS系統的總體結構如圖1所示。INS提供速度、位置和姿態信息,GPS提供速度和位置信息,通過Kalman濾波得到系統狀態誤差,狀態誤差對慣性導航系統進行補償,最終得到導航結果。同時,對新型BPNN進行訓練,將慣性導航系統的輸出信息作為BPNN的輸入信息,將Kalman濾波器的輸出信息作為BPNN的標準輸出信息。如圖2所示,在GPS信號失效時,BPNN將代替 GPS和Kalman濾波器對慣性導航系統輸出進行校正,減緩純慣性導航期間的誤差發散。
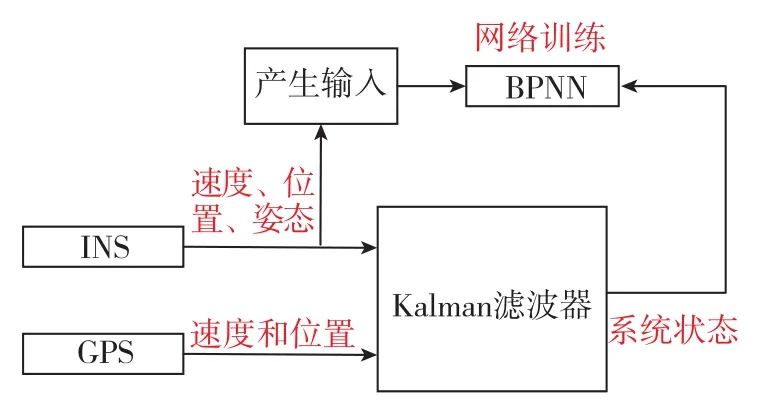
圖1 GPS信號正常時的系統原理圖Fig.1 Schematic diagram of system when GPS works well
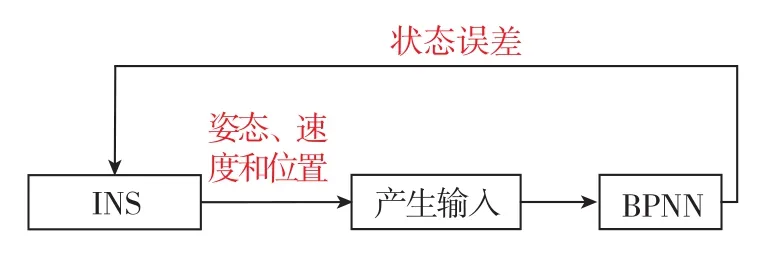
圖2 GPS信號失效時的系統原理圖Fig.2 Schematic diagram of system when GPS loses efficacy
2 神經網絡I/O模型設計
本文利用神經網絡擬合輸入與慣性導航解算誤差之間的非線性關系,設計了結構簡單、具有較強映射關系的I/O模型,該模型是提高神經網絡預測能力的關鍵。
在飛艇上升和下降階段,位置和速度信息最為關鍵。因此,新模型只需分析INS的位置誤差和速度誤差。位置誤差以向量的形式表示如下
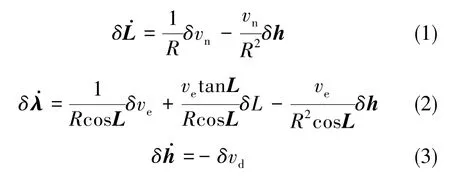
L、λ、h分別為緯度、經度、高度,δL、δλ和δh分別為導航坐標系下北向、東向和天向的位置誤差,vn、ve、vd分別為導航坐標系下北向、東向和天向的速度,δvn、δve和δvd分別為導航坐標系下北向、東向和天向的速度誤差,且有(R為地球半徑與載體高度之和)。由此可得速度誤差和位置誤差之間存在非線性映射關系,這種映射關系可以用式(4)表示

此外,速度誤差和姿態誤差之間也存在映射關系
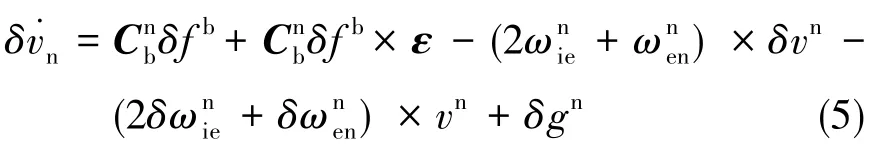
式(5)中,ε為傾斜角向量,δvn為導航坐標系下的速度誤差,為機體坐標系到導航坐標系的轉換矩陣,也被稱作姿態陣。因此,速度誤差可以由速度和姿態信息計算而得,用式(6)表示

根據慣性導航的解算流程容易得出:速度信息影響位置信息,姿態信息確定的捷聯矩陣又影響速度信息,因此姿態和速度信息與位置信息之間存在非線性映射關系。這種映射關系可以用式(7)表示, 而式(8)和式(9)可以由式(4)、式(6)和式(7)推導而得。由上述分析可知,位置誤差和速度誤差由慣性導航的姿態和速度信息產生。
新的輸入/輸出模型如圖3所示。合理設計神經網絡的輸入和預測周期,簡化網絡結構和計算規模。預測周期與傳統Kalman濾波周期相同,均為1s。將1s內的速度均值和1s內的姿態變化量作為神經網絡的輸入信息,將1s末的組合導航位置與慣性導航位置的差值,以及1s末組合導航速度與慣性導航速度的差值作為神經網絡的輸出信息。陀螺和加速度計的零位誤差及隨機白噪聲,均存儲在神經網絡隱層和輸出層的權重信息中。
3 改進的BPNN算法設計
目前神經網絡的模型有很多,其中BPNN算法是最為常用的學習算法,但是BPNN算法存在學習時間長、學習穩定性差等缺點[7-8]。本文對傳統BPNN算法進行了改進,有效提高了傳統BPNN算法的信息存儲能力、非線性擬合能力和收斂速度。
本文設計了基于偏移參量和縮放因子的激活函數,對傳統tan-sigmoid激活函數進行了重新設計,使各個神經元的激活函數可以實現動態變化,其式如式(14)所示。 式(14)中,T為縮放因子,θ為偏移參量,參數T和θ可以確定每個神經元的響應特性。式(12)中的誤差函數是關于T、θ和W的函數,可以用式(15)表示。根據最速下降法,應調整T、θ和W, 以得到E的最小點。 式(16)~式(18)表示T、θ和W的更新方程。其中,Lw、Lr和Le為W、T和θ的 學 習 率, ?E/?W(t)、?E/?T(t)和?E/?θ(t)為W、T和θ的誤差函數E的增長率,αW、αT和αθ為連接權值W、縮放系數T和位移參數θ的動量項。動量項能夠減弱震蕩,提高收斂速度。
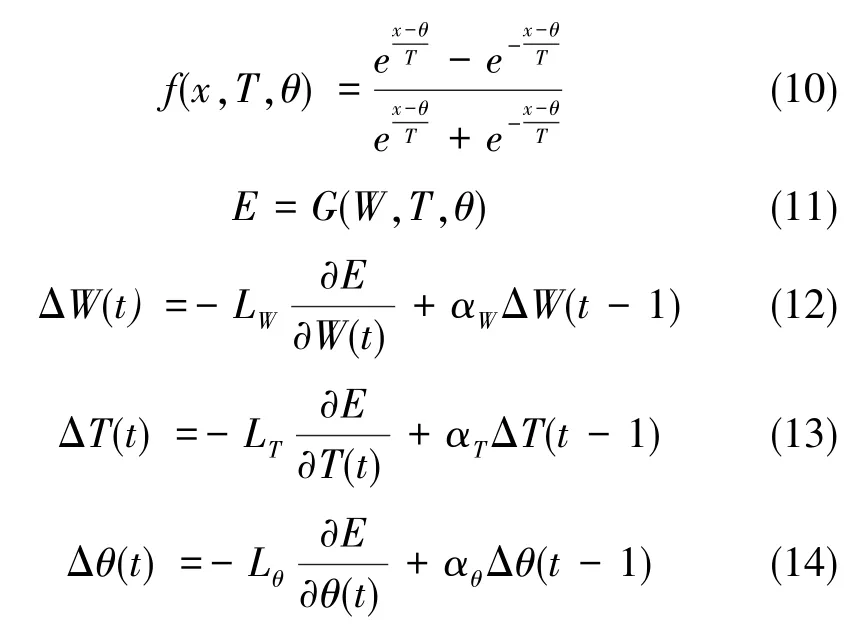
對于傳統的BPNN算法,學習率在學習過程中恒定不變[9-10]。為加快網絡收斂速度,應根據學習過程對學習率進行調整,使學習率動態變化,如式(15)所示。
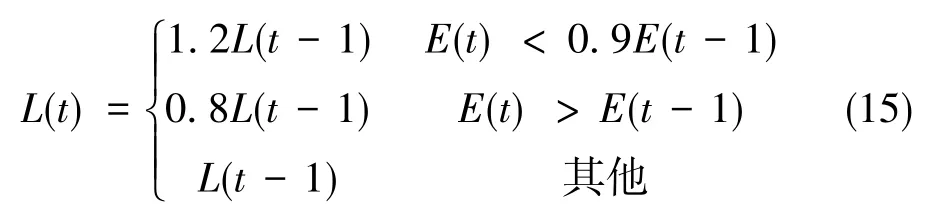
4 結果分析
本文通過仿真實驗和跑車試驗來驗證所提方法的有效性。為測試系統在純慣性導航期間提供可靠位置和速度信息的能力,在不同的飛艇動力學位置人為設置了GPS中斷。表1列出了用于仿真實驗和跑車試驗的INS和GPS的規格。
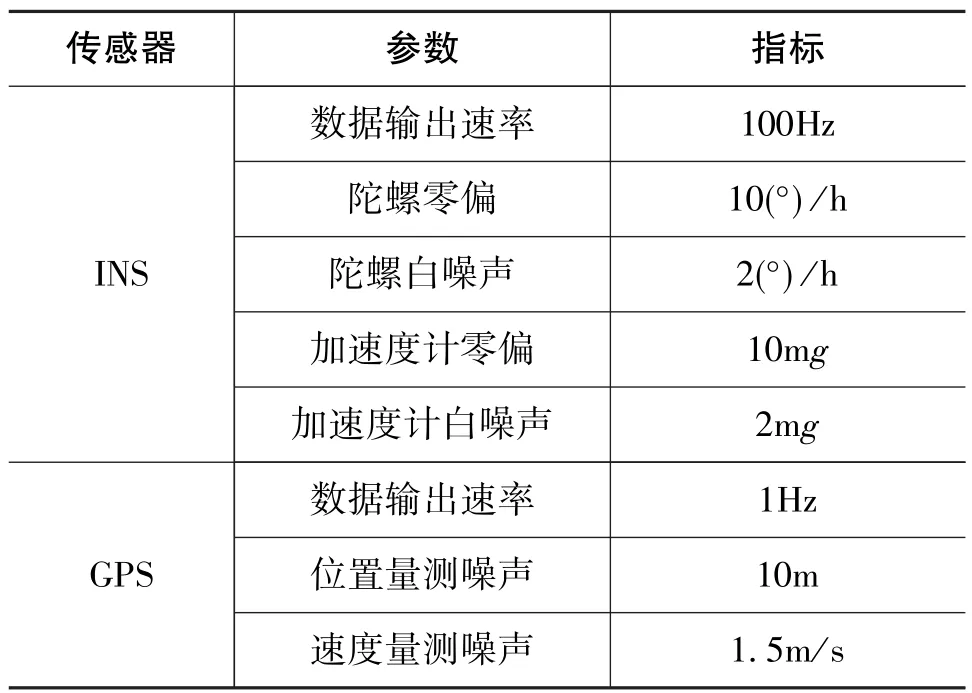
表1 INS和GPS的性能指標Table 1 Specifications of low-cost INS and GPS
4.1 仿真實驗
為了更好地訓練BPNN,設計了訓練軌跡。訓練軌跡包括110°的勻速圓周運動、-110°的勻速圓周運動和160°的勻速圓周運動,它們模擬了飛艇升降過程中的大幅度轉彎運動,以及3段勻加速直線運動和3段勻減速直線運動。訓練軌跡如圖4所示,持續時間為132s。
為檢驗所訓練的BPNN的性能,設計了一條預測軌跡,如圖4所示。預測軌跡與訓練軌跡不同,并且包含2段30s的GPS中斷(圖中虛線部分)。
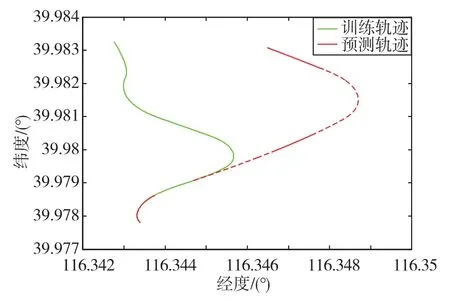
圖4 訓練和預測軌跡Fig.4 Trajectories of training and predicting
圖5、圖6分別展示了仿真實驗使用改進BPNN、傳統BPNN和純慣性導航在2次GPS失效期間的位置誤差和速度誤差。顯然,在GPS中斷期間,改進BPNN和傳統BPNN的導航精度均比純慣性導航的精度更高。此外,從圖5、圖6可以看出,在第2個GPS失效段,傳統BPNN的誤差比改進BPNN的誤差小,但傳統BPNN與改進BPNN相比只有輕微的改進。從平均水平來看,針對位置誤差和速度誤差,改進BPNN比傳統BPNN的性能更加優越。
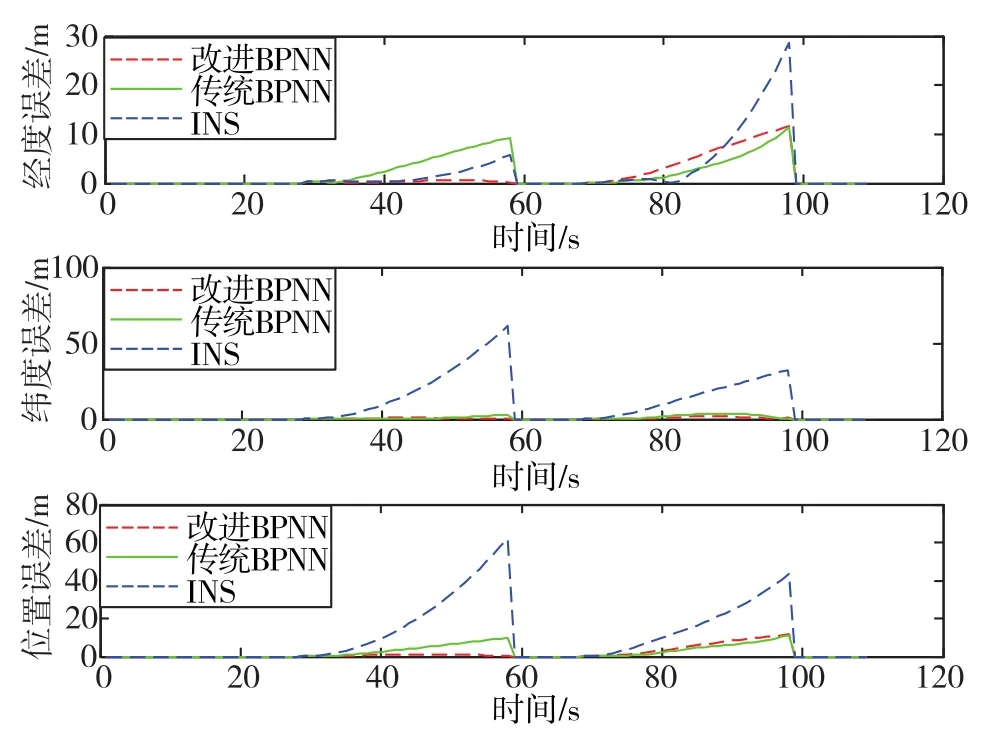
圖5 GPS失效期間的位置誤差Fig.5 Position errors when GPS loses efficacy
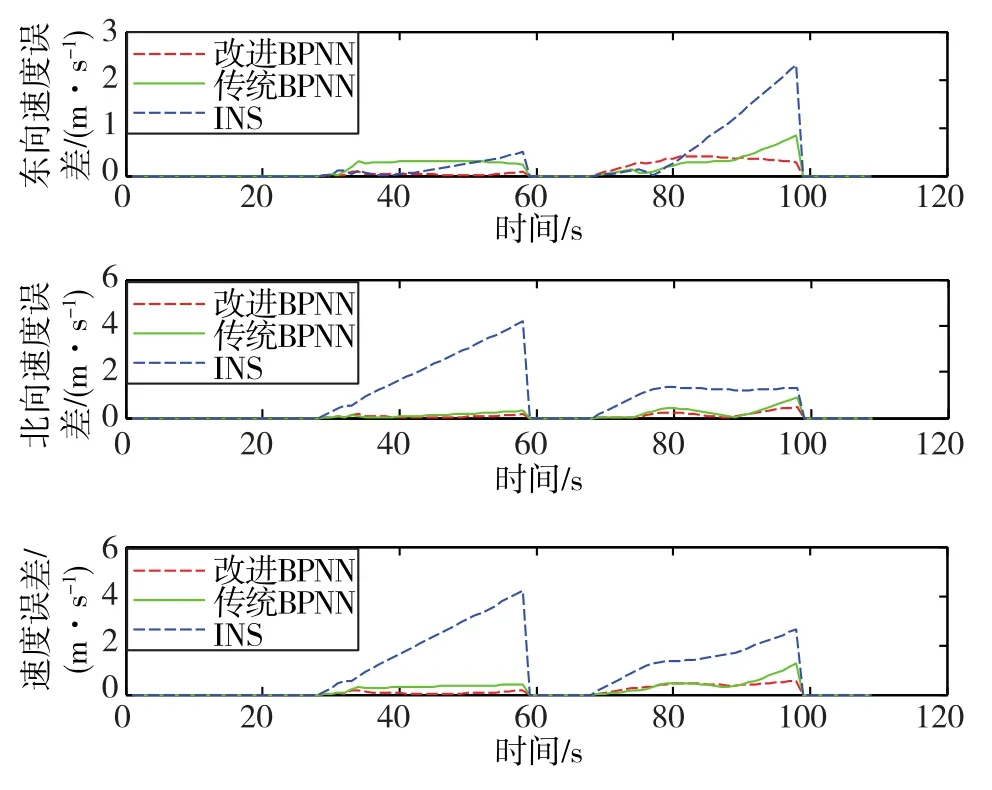
圖6 GPS失效期間的速度誤差Fig.6 Velocity errors when GPS loses efficacy
4.2 跑車試驗
跑車試驗的軌跡如圖7所示。藍色部分是訓練階段,其中包括4個轉彎運動和部分直線運動。該軌跡的5段虛線部分是人為的30s GPS中斷,黑色部分是GPS信號的正常段。
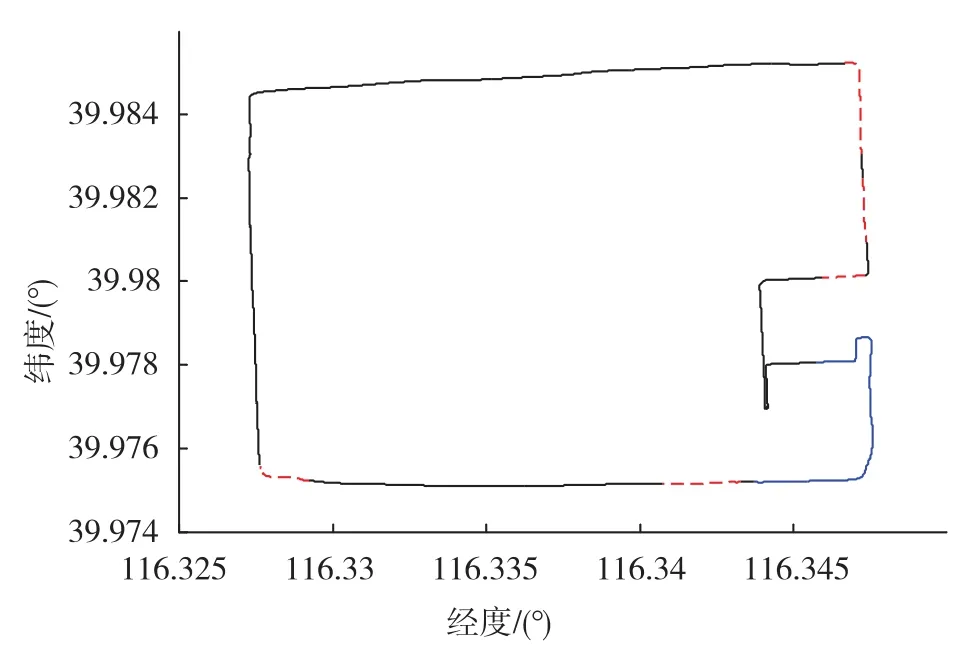
圖7 跑車軌跡Fig.7 Trajectories of the vehicle
圖8、圖9展示了跑車試驗使用改進BPNN、傳統BPNN和純慣性導航解算的位置誤差和速度誤差。顯然,改進BPNN和傳統BPNN在GPS中斷階段的導航精度比純慣性導航精度更高。此外,對于速度誤差和位置誤差,改進BPNN比傳統BPNN要小。表2展示了在4段30s GPS中斷期間使用不同方法的速度誤差和位置誤差的匯總。與INS相比,改進BPNN的速度誤差和位置誤差分別降低了89.5%和88.0%。與常規BPNN相比,改進BPNN的速度誤差和位置誤差分別降低了58.4%和63.3%。
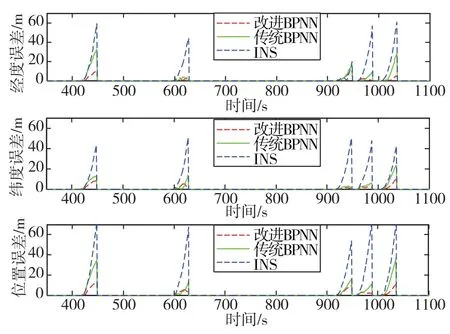
圖8 GPS失效期間的位置誤差Fig.8 Position errors when GPS loses efficacy
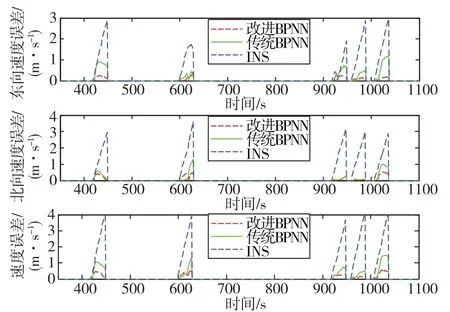
圖9 GPS失效期間的速度誤差Fig.9 Velocity errors when GPS loses efficacy
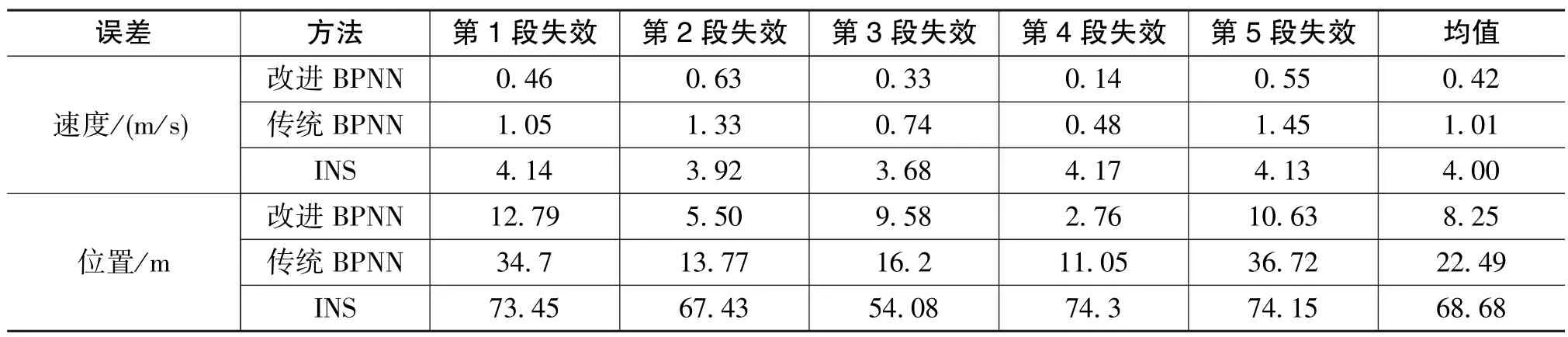
表2 30s GPS中斷、不同方法的速度誤差和位置誤差匯總Table 2 Summary of velocity errors and position errors for 30s GPS outages using different methods
5 結論
本文提出了一種改進的BPNN慣性導航算法,用于補償慣性導航在飛艇上升和下降階段的位置誤差和速度誤差。仿真實驗和跑車試驗的結果表明,新算法在30s GPS失效時間內的位置誤差小于15m,速度誤差保持在0.7m/s以下。與INS相比,改進BPNN慣性導航算法可以將導航誤差降低至少85%。

