基于模糊狀態觀測器的燃氣輪機轉速傳感器故障檢測研究

趙 駿,朱嶸嘉,陳 鵬

(第七○三所無錫分部,江蘇 無錫 214151)

轉速傳感器是燃氣輪機控制系統的重要參數輸入端。由于燃氣輪機轉速傳感器的工作環境存在高溫、鹽霧、油霧等惡劣因素,導致其成為控制系統中最容易出現故障的環節之一[1-3]。錯誤的轉速信號如能及時檢測,則可利用備份傳感器或重構控制律來確保系統繼續運行,否則極易使控制系統執行降工況、停機等保護動作。因此,及時準確的檢測出故障具有重要工程意義。

燃氣輪機在正常運行時,源于進口空氣溫度、壓力、燃油調節閥前的壓力波動和負載等因素的不同,即使在相同工況下,其轉速最高值和最低值也可相差總量程的1%～2%。另一方面,水霧、油霧、灰塵、及含鈉、硫、釩等雜質的燃料燃燒產生的腐蝕和老化,也會導致轉速測量值逐漸偏離初始范圍[4]。轉速傳感器故障診斷不僅要迅速、準確,更要將真實故障和上述燃機的特性變化及擾動識別開來。

目前,傳感器故障檢測方法較多,基于模型解析的故障檢測法由于硬件結構簡單,成本低等優點受到了廣泛關注,但由于需要精確的對象模型,使其面對非線性系統和具有不確定擾動的系統變得難以處理。例如,基于Kalman濾波算法[5-7]解決多傳感器故障的檢測,但對模型的線性化處理不可避免的降低了檢測準確度,文[8]將檢測范圍減少至某一工況區間,以此減少模型不確定性的影響,卻限制了故障檢測算法的適用范圍。

本文將模型參考自適應與模糊理論相結合,提出了穩定的非線性轉速狀態觀測器的設計方法,解決了傳統模型觀測器在低轉速或模型不精確時易產生的誤差累計和觀測偏移的問題,并根據轉速故障規律,在決策階段設計自適應閥值,提高了故障檢測的魯棒性,避免了燃氣輪機本身特性變化及擾動對故障檢測的影響。仿真結果表明該方法能高精度跟蹤傳感器輸出,及時準確地進行轉速傳感器故障診斷。

1 燃氣輪機動態模型

根據燃氣輪機工作所遵循的氣動熱力學定律,忽略燃機熱效應,建立如下非線性模型[9]來表示實際燃氣輪機運行狀態:

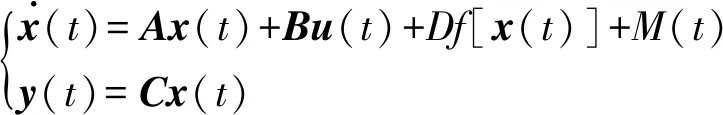
(1)

式中:u為系統輸入,表示燃油流量,x=[NhNp]T為系統可測狀態量,Nh、Np分別表示燃氣輪機高壓壓氣機轉速及動力渦輪轉速相對于設計點的偏差量;f(x)為未知非線性光滑函數,且f(0)=0;y與x同維,為系統輸出向量;M(t)為未知有界故障函數;A、B、C、D為已知適當維數可觀矩陣。

根據燃氣輪機原理可知,雖然進口空氣溫度、壓力和進排氣損失均會對燃氣輪機轉速值產生影響,但在一段時間區間內,可以視上述因素的影響基本不變,即在穩態工況下,可用燃油流量映射燃機轉速。

針對燃氣輪機轉速傳感器故障,我們可作如下假設:

①M(t)為有界故障向量,存在常數Γ1∈R,使得以下不等式滿足:

‖M(t)‖≤Γ1‖x(t)‖

(2)

②u(t)為有界系統輸入量,存在常數Γ2∈R,使得以下不等式滿足:

‖u(t)‖≤Γ2‖x(t)‖

(3)

③f(x)為系統非線性函數,且存在已知常數θt和θt,使得以下不等式滿足:

對于系統(1)中的不確定部分f(x),利用模糊邏輯系統來盡可能跟蹤非線性函數輸出。已經證明,模糊函數可逼近任意有界連續的非線性函數[10],對于在緊集Ω上的函數f(x),給定任意正數ε>0,存在模糊函數ξ(x|w)=wTG(x)和最優權重向量w*,滿足

supx∈Ω|f(x)-ξ(x|w*)|<ε

(4)

式中:Ci=[c1,c2,…,cn]T與x同維,為中心向量;σi為高斯函數的寬度。

在以上討論中,本文未要求式(4)中的ε為任意小,這樣做是因為實際中要找到滿足逼近非線性函數至任意小的模糊系統是比較困難的,通常,定義逼近誤差ε比觀測器的跟蹤精度高一個數量級即可。

2 狀態觀測器設計

首先,針對系統(1)利用對等空間法建立非線性狀態觀測器,觀測器結構如下圖1所示。利用模糊函數輸出逼近非線性函數f(·),當系統無故障M(t)=0,給出觀測器形式為:

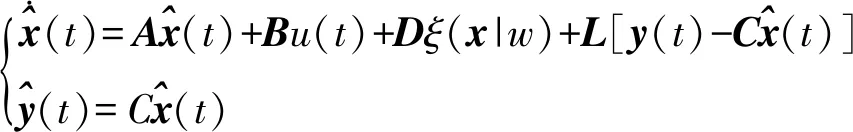
(5)

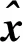
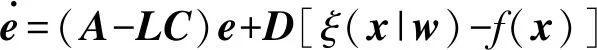
(6)

定義模糊最優權重向量w*,及最小逼近誤差ω,則有

(7)

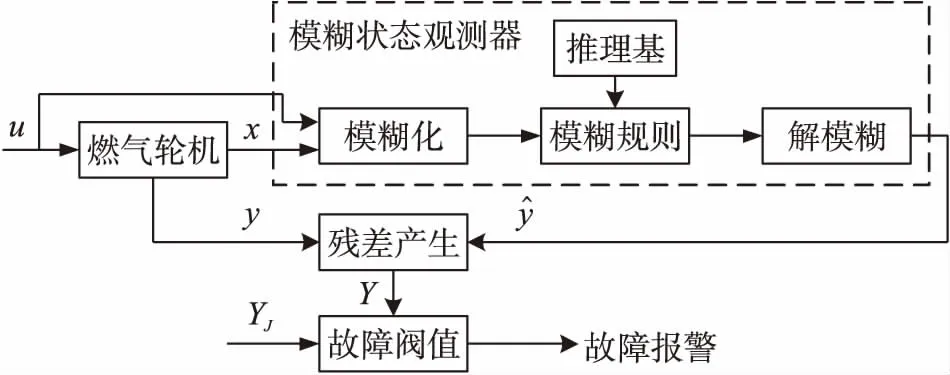
圖1 模糊狀態觀測器結構圖

由模糊函數ξ(x|w)的定義,將式(7)代入式(6)得,

(8)

通過對模糊狀態觀測器的穩定性進行分析,給出以下結論。

定理1對于給定的非線性系統(1)及模糊狀態觀測器(5),如存在標量Z>0和對稱陣Ψ>0,在使得如下代數Riccati方程[11]

(9)

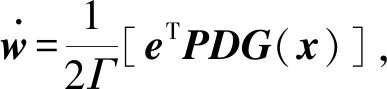
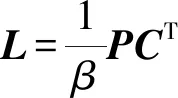
(A-LC)TP+P(A-LC)+Ψ+ZI=0

由于Z>0,則有,

(A-LC)TP+P(A-LC)+Ψ<0

(10)

給定如下形式Lyapunov函數

V=eTPe+Γ(w-w*)T(w-w*)

對Lyapunov函數求導,代入式(6)得

eT[(A-LC)TP+P(A-LC)]e+

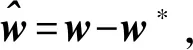
(11)

則,有

(12)

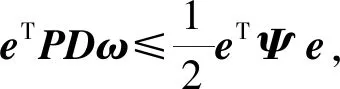
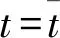
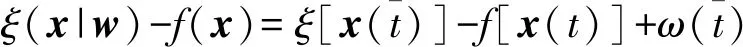
則誤差方程形式為:

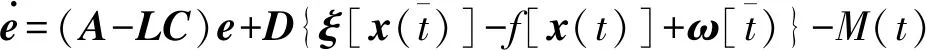
(13)

由式(1)和式(13)組成增廣系統

式中:

引理1對任意給定的合適維數的實矩陣Σ1,Σ2,存在δ∈R,下述不等式成立

選擇Lyapunov函數

式中:P1為已知正定對稱陣。函數V的全導數為

給定Λ=[0I],由假設1和引理1可得,存在δ1∈R

由假設3和微分中值定理,可得|f(x)|≤θt|x(t)|,其中θt=max{|θt|,|θt||t=1,2,…,n},由此

|F(x)|=|f(x)+D-1M(t)|≤θt|x(t)|+
Γ1D-1|x(t)|=Γ3|x(t)|

式中:Γ3=θtI+Γ1D-1。則可得,存在δ2∈R

又由假設3可知,對于給定的ΔS有界,所以有

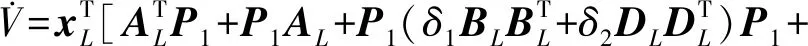
(14)

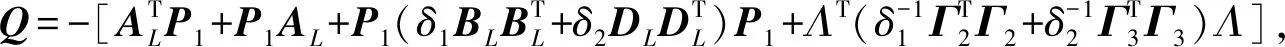
如上文所述,狀態觀測器基于燃氣輪機非線性模型建立,而燃氣輪機長時間運行所產生的部件磨損、侵蝕和老化,均會引起機組轉速和燃油量的對應關系產生變化,增加模型誤差。根據實際運行經驗,一般運行3 000 h,需根據實際數據對非線性模型進行修正。

3 自適應閥值設計

(15)

實際中,由于船用燃氣輪機轉速傳感器安裝在高溫、油霧和鹽霧腐蝕的環境,所以通常采用環境適應性強的磁電式傳感器。其特性表現為,低轉速時,信號強度較弱,在燃氣輪機起動初期甚至存在一定的采樣不穩定區間;隨著轉速的上升,信號強度和穩定性會逐漸增加,高轉速時,正常轉速信號的波動反而相對減小。同時,由于轉速齒輪加工誤差以及傳輸線路信號干擾的影響,轉速信號在在正常情況下也存在小幅波動。

另一方面,由于未建模因素影響,觀測器估計值與實際測量值的殘差在轉速信號穩定且無故障時也不為零,而且在燃氣輪機加速或減速的動態情況下,模型不可避免會存在一定的跟蹤時滯。因此,采用傳統的固定閥值[12]的檢測方法,不僅閥值參數難以確定,還易出現錯檢和漏檢的情況。

綜上所述,本文提出一種基于知識庫的閥值自適應設計方法,根據獲取的轉速值,自適應調整閥值范圍,在低轉速和加減速過程中,閥值的設定相對較大,以避免由于信號擾動而發生誤判,而轉速進入穩定區間后,故障閥值設定應該相對減少。

給定自適應調整公式為:

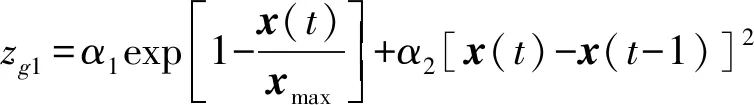
式中:xmax為最大轉速值;α1和α2為對應調節系數,根據燃機起動過程及加速或減速時,轉速波動的實際情況進行修正。zg0為理想條件下的基準閥值,可根據傳感器和轉速采集模塊的采樣誤差進行定義,取5倍～8倍的采樣誤差。zg1為自適應調整部分,主要目的是克服低轉速擾動區的不確定性和削弱跟蹤時滯的波動影響。

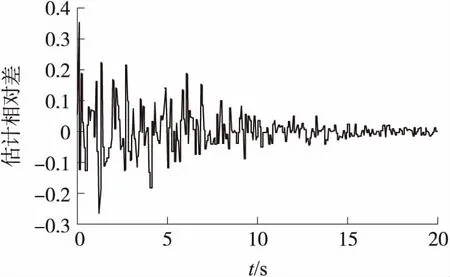
圖2 起動時估計相對差曲線(轉速傳感器正常)

4 仿真驗證

利用某三軸燃氣輪機模型[13]來代替實際未知被控對象,不考慮干擾影響,以高壓壓氣機轉速和動力渦輪轉速為狀態變量,對模型進行歸一化處理,可得參數表達式如下:

(16)

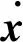
選取高壓壓氣機轉速傳感器常發生的典型故障,圖3為燃氣輪機起動過程中,在第3 s發生轉速傳感器信號恒減損故障。圖5為運行時,在第30 s～40 s,發生傳感器短路故障。

通過高壓轉速估計相對差曲線(圖4)可以看出,在燃氣輪機起動初期,在低轉速時,正常的轉速傳感器輸出信號存在波動,估計相對差較大,10 s以后相對差迅速減少,20 s后趨于穩定,自適應故障閥值的設置有效的避免了初始情況的故障誤報。30 s時刻,發生轉速傳感器信號減損故障時,估計相對差即發生變化。

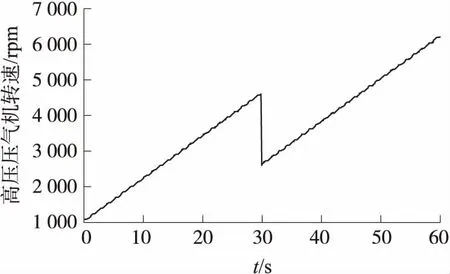
圖3 傳感器恒減損故障曲線

圖4 恒減損故障估計相對差曲線

通過圖6可知,在穩定工況運行時,自適應閥值基本穩定在0.1附近,在30 s～40 s,發生傳感器短路故障時,估計相對差遠遠大于閥值,快速檢查到故障的發生。

同時,將提出的基于模糊狀態觀測器故障檢測方法和傳統基于擴展卡爾曼濾波器的方法對診斷正確率進行比較,在相同樣本情況下,選取穩態下傳感器恒減損故障(故障1)和短路故障(故障2)以及起動中傳感器恒減損故障(故障3)和短路故障(故障4)共4組故障數據進行仿真,結果如圖7所示。

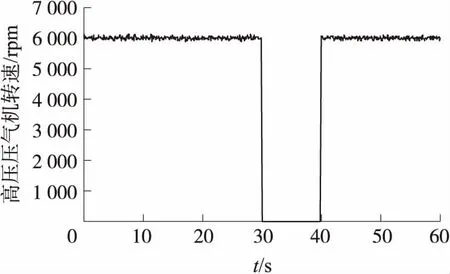
圖5 傳感器短路故障曲線

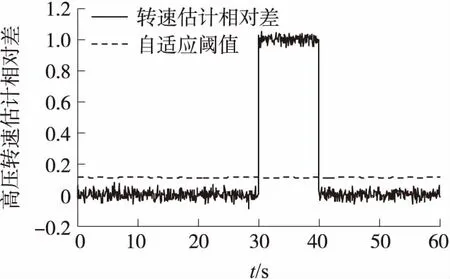
圖6 短路故障估計相對差曲線

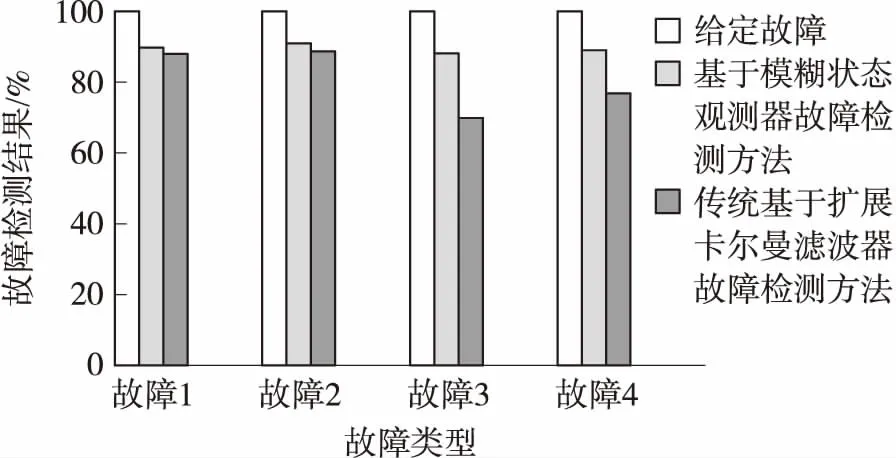
圖7 兩種故障檢測方法故障識別率對比

由圖7可得,穩態情況下,兩種故障檢測方法對燃氣輪機轉速傳感器故障檢測的識別率相近,均在85%以上。但在起動過程中,基于模糊狀態觀測器故障檢測方法較基于擴展卡爾曼濾波器的方法具有更高的準確率。

5 結論

本文利用模糊理論建立非線性轉速狀態觀測器,并根據轉速故障規律,提出了自適應閥值的設計方法,解決了傳統模型觀測器在低轉速或模型不精確時易產生的誤差累計和觀測偏移的問題,通過轉速估計相對差和故障閥值的比較,能準確快速的檢測傳感器故障,避免了燃氣輪機本身特性變化及擾動對故障檢測的影響。試驗結果證明,該方法能實時準確地檢測傳感器故障,且在動態過程中,較基于擴展卡爾曼濾波器的方法有更高的準確率。