基于KM-FNN的無線傳感器網絡缺失數據重建算法*

武加文,李光輝*

(1.江南大學物聯網工程學院,江蘇 無錫 214122;2.物聯網技術應用教育部工程技術研究中心,江蘇 無錫 214122)

通過將客觀物理世界與信息世界緊密的相聯,無線傳感器網絡(Wireless Sensor Network,WSN)極大地提高了人們對真實世界的認識能力[1]。然而,在環境監測領域,WSN通常被部署于無人監管、氣候復雜的野外環境,一方面,受到低成本傳感器節點資源的限制,例如電池功率、計算存儲能力以及通信帶寬,這使得節點產生錯誤數據的概率很大。另一方面,數量龐大地傳感器節點通常隨機部署在環境惡劣的外界環境,伴隨著極端氣候的影響,如狂風,暴雨,冰雹等,一些節點發生故障也是不可避免的。因此,在長期使用過程中,WSN經常發生數據缺失現象[2]。若不精確重建這些缺失數據,可能會影響整個網絡數據的可靠性以及監測數據流的完整性。例如,當監測環境發生事件(如森林火災、水質或空氣污染等)時,不可靠且不完整的數據可能導致系統無法實時檢測到類似的自然災害,從而造成重大損失。因此,快速準確地重建缺失數據具有重要意義。

關于WSN數據重建方法,國內外學術界已有諸多成果[3]。現有的WSN數據重建方法主要是利用感知數據的先驗信息,這在一定程度上可以恢復丟失的數據。利用節點間的空間相關性,文獻[4]提出了一種克里金插值方法,通過考慮缺失數據的空間位置及分布信息,利用不同系數加權平均得到待插點的估計值。文獻[5]在文獻[4]的基礎上,加入貪婪算法用以去除誤差評估最優的傳感器節點,從而有效地減少了部署的傳感器節點,降低了時間復雜度。文獻[6]將節點的感知數據映射至圖表,并引入互連矩陣和系統圖等概念,構建了一個傳感器網絡實時預測的模型用以重建缺失值。文獻[7]提出了一種基于二次規劃的感知數據恢復的方法。該方法將重建過程轉換為有界約束二次規劃問題,并通過求解Armijo規則的二次規劃問題,從而有效地恢復了數據。文獻[8]提出了一種數據挖掘的方法(CARM)重建缺失數據。該方法通過關聯規則挖掘感知數據得到節點之間的頻繁模式,以恢復缺失值。

基于傳感器節點的時間相關性與空間相關性,文獻[9]提出了基于時間相關性的數據重建算法LIN和基于空間相關性的數據重建算法MR。LIN考慮到數據的時間相關性,連續時刻的節點數據是近似的。如果當前時刻數據缺失,可以利用前一時刻和后一時刻的數據來估計當前時刻的數據。MR主要是利用節點部署的空間相關性,即相鄰節點的感知數據具有相似性,因此,基于鄰居節點的數據重建目標節點的缺失數據。目前,已有多種機器學習方法被用來解決數據缺失問題,如決策樹、貝葉斯法、期望值最大化、回歸法等。其中,大多數方法是利用已有的正常數據作為訓練樣本,從而建立預測模型,以估計缺失數據[10]。然而,一旦預測值不精確,將導致數據重建的精度受到累積誤差的限制。

針對上述問題,本文提出了一種基于自適應的K-均值算法與模糊神經網絡相結合的WSN缺失數據重建算法(KM-FNN)。KM-FNN應用于分簇式WSN的簇頭節點上,使用模糊神經網絡模型重建缺失數據并引入自適應機制用來及時更新訓練模型。KM-FNN可以實時向基站匯報存在數據缺失的節點序號以及重建后的完整數據流。實驗結果表明,相較以往同類算法,KM-FNN具有更精準的缺失數據重建精度。

1 基本概念

1.1 分簇式無線傳感器網絡模型結構

本文基于分簇式WSN進行仿真實驗,將鄰近區域內的節點分為一個簇,每個簇包含簇頭節點和一定數量的成員節點。通常,簇內成員節點只負責采集感知數據,并將數據傳送至簇頭節點,由簇頭節點負責分析與處理這些數據[11],其結構如圖1所示。

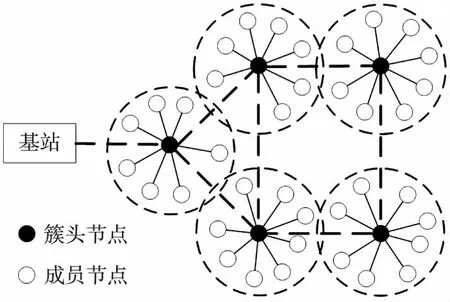
圖1 分簇式WSN結構

1.2 模糊神經網絡

模糊神經網絡FNN(Fuzzy Neural Network)是一種用于預測的神經網絡系統。其中,隸屬度與隸屬度函數是FNN中最基本的概念[12]。隸屬度是指某一元素u隸屬于某一模糊子集A的程度,見式(1)。隸屬度函數是用來計算元素隸屬度的函數,一般為正態函數。

(1)

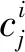
FNN的自適應力極強,可以自動更新模糊子集的隸屬函數。基于規則,其推理規則如下[13]:

(2)

1.3 性能評價指標

本文選用均方誤差和決定系數作為WSN缺失數據重建算法的性能評價指標。其中均方誤差MSE(Mean-Square Error)表示預測值與被預測值之間的差異程度,見式(3)。一般情況下,MSE越小,表明預測值與被預測值之間差異程度越小。MSE越大,表明預測值與被預測值之間差異程度越大。而決定系數(coefficient of determination)R2表示所建立的預測模型對被預測值的擬合程度。R2的取值范圍一般在區間[0,1]。若該值越接近1,表明模型的擬合程度越高,即性能越好。相反,越接近0,表明模型的性能越差。

(3)

(4)

式中:n表示樣本數目,與分別為第i個樣本的被預測值與預測值。

2 KM-FNN數據重建算法

2.1 算法概述

通常情況下,在分簇式WSN中,傳輸至簇頭節點的數據中會存在一定量的數據缺失。若能在簇頭節點將數據發送至基站前重建缺失數據,這樣會大大節省了后續的工作。同時考慮到真實的WSN受外界自然環境的影響較大,導致感知數據分布的情況隨著時間的推移產生了復雜的變化。因此,本文提出了基于自適應的WSN缺失數據重建算法KM-FNN。KM-FNN首先使用傳輸至簇頭節點的初始感知數據建模用以預測缺失值,然后引入自適應機制用來在線更新模型以適應感知數據的變化。自適應機制的實現主要依賴于滑動窗口的引入以及模型的在線更新準則KM算法。KM-FNN運行在簇頭節點上,能夠實時自適應地重建節點的數據缺失,并向基站匯報存在缺失值的成員節點編號以及重建后的完整數據序列。

2.2 FNN的建模過程

模糊神經網絡的優勢是具有較強的自適應能力和并行分布式的數據處理能力。因此,采用模糊神經網絡對節點間的時空相關性建模。將WSN部署初期(假設此時無缺失數據)的目標節點i和其鄰居節點的感知數據作為訓練數據集,訓練數據集可以被劃分為Train={TX;TY}。TX表示訓練數據輸入,TX={xj,t:j=1,2,…,m;t=1,2,…,w},TY表示訓練數據輸出,TY={xj,t:t=1,2,…,w}。其中,j表示節點序號,t表示時序。m表示節點i的鄰居節點的個數,w表示節點i的感知數據的個數。基于FNN算法的WSN數據重建的算法流程參見圖2。

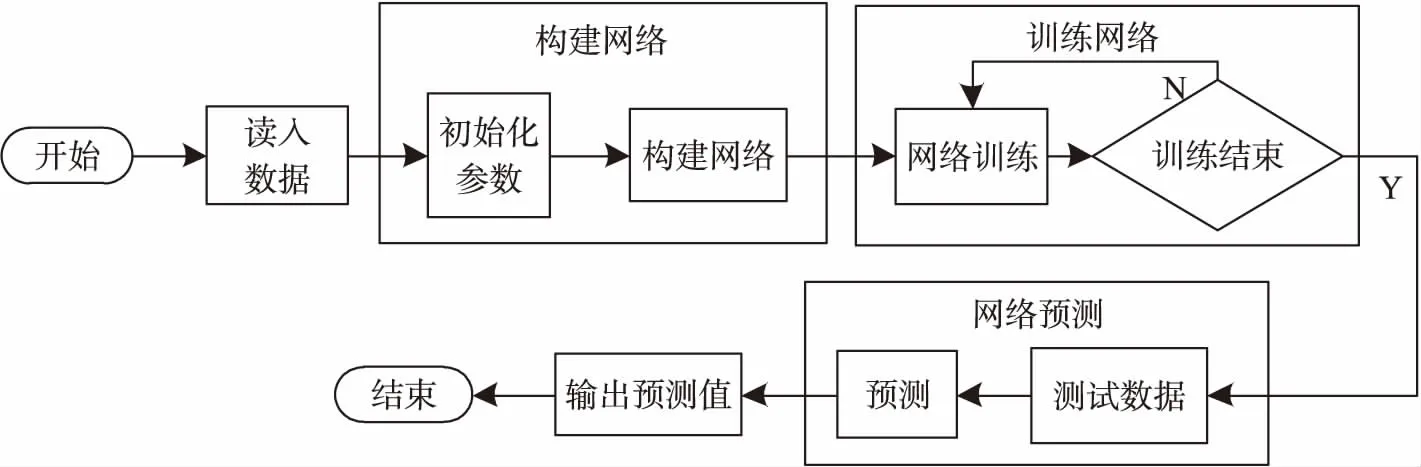
圖2 FNN建模流程

如圖2所示,網絡的輸入,輸出節點數由TX與TY的維度而確定,并隨機初始化模糊隸屬度的函數中心c,寬度b等參數。綜上,FNN建模的具體方法如下:首先,根據數據集的劃分情況確定網絡結構,初始化網絡參數,并初始化隸屬函數和模糊規則。其次,使用訓練集訓練得到網絡模型,并進一步更正隸屬函數和模糊規則。最后,在訓練模型中輸入測試集并輸出預測值,完成缺失數據的重建。

2.3 自適應機制的實現

在環境監測領域,真實的WSN易受外界自然環境的影響導致感知數據的分布情況隨著時間的推移產生了復雜的變化。如果一直采用固定的神經網絡模型用于缺失數據的重建,則該算法的魯棒性以及適用性會受到很大影響[14]。由于節點數據在傳輸過程是以數據流的方式傳輸,其傳輸方式是實時的,連續的。為了更好地模擬算法在WSN上的真實應用過程,引入了滑動窗口機制,針對節點的數據流選取了一個固定長度的窗口,用于觀測節點最近一個時間段內采集的數據流的變化狀況。

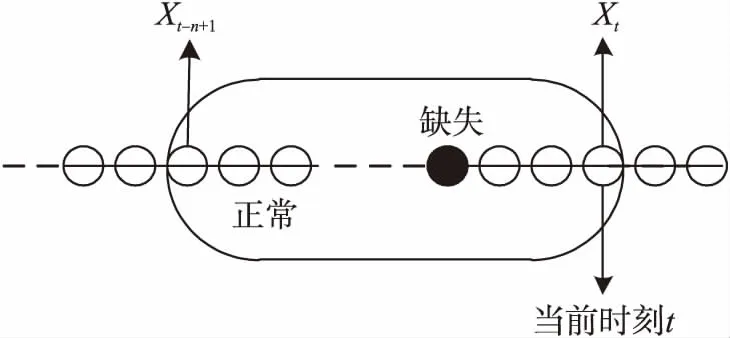
圖3 數據流滑動窗口模型

圖4表示在IBRL數據集中1號節點于2004年3月1日0:00～7:00和12:00～20:00的溫度分布情況。IBRL數據集來自于2004年2月28日到2004年4月5日期間部署在Intel Berkeley實驗室內的無線傳感器網絡,共包含54個節點。每個節點以31 s的采樣周期采集四種屬性數據,包括溫度、濕度、光照及電壓值。圖4(a)表示0:00～7:00時間段內的溫度隨時間的變化情況,圖4(b)表示12:00～20:00時間段內的溫度隨時間的變化情況,由圖4可知,隨著時間的流逝,數據的分布情況發生了較大的變化。因此,若采用固定不變的模型預測缺失數據會導致重建精度的累積下降。

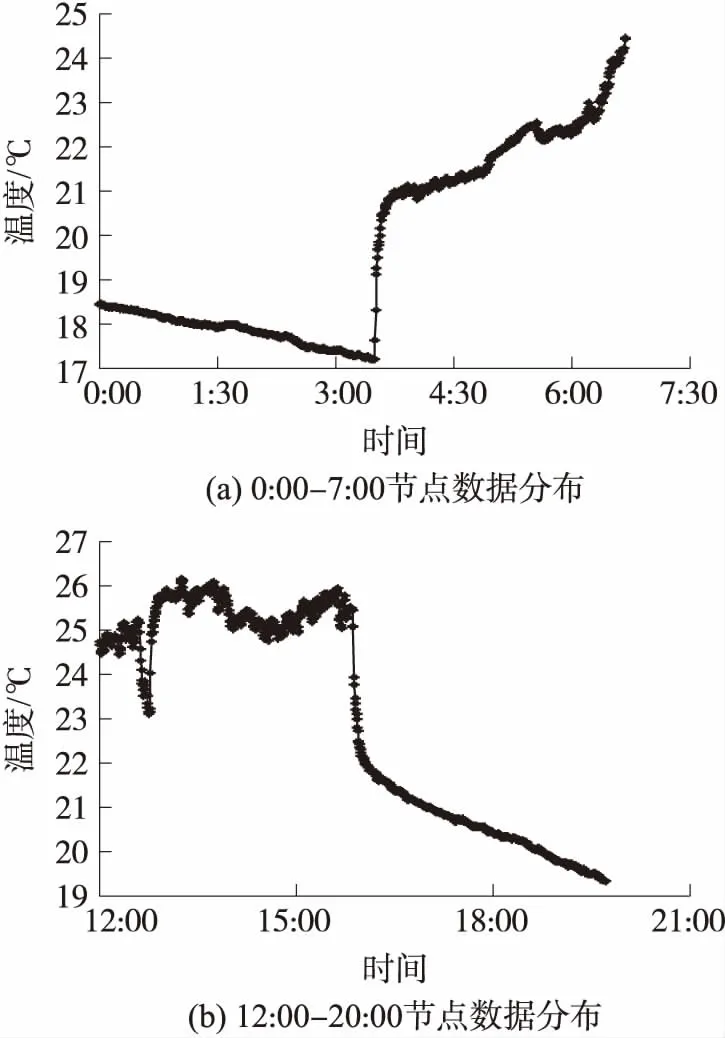
圖4 不同時間段的數據分布情況

KM-FNN使用K-均值算法(k-means)作為更新準則,其思想是把數據分配至距離其最近的類中心的歸屬類,類中心由屬于該類的全部數據決定[15]。結合K-均值算法,提出的基于數據分布的自適應算法KM的偽代碼見表1。其中,x表示待加入滑動窗口的數據,x之前的數據被劃分為k類,每類中包含Mh個數據,其中心數據為AMh,其中h=1,2,…,k。

如表1所示,KM的實現過程如下。當新數據加入滑動窗口時,首先判斷該數據是否缺失。若不缺失,則快速判斷其所屬的類別,并更新所屬類別的中心數據,然后計算完整數據的MSE,該值為Eb。當該數據缺失時,使用當前的FNN模型預測該數據,并將預測值作為新數據加入滑動窗口中。重復上述操作,直到所有數據處理完畢。

綜上所述,KM-FNN的實現步驟如下。首先在簇頭節點中匯集初始階段的N個成員節點的感知數據,并將各個節點數據均按照K-均值算法的思想,劃分為k類,并分別計算每類中單個數據與中心數據的MSE,然后求k個MSE的平均值,得到總體MSE值Ea。對于待測試的成員節點i,設其鄰居節點的個數為mi,然后根據節點i和其鄰居節點的感知數據建立FNN模型,表示為FNNi。即初始階段,簇頭節點中建立N個網絡模型。在下一時間段內,簇頭節點收到節點i的測試數據x=x1,x2,…,xq。

表1 KM自適應算法

表2 KM-FNN數據重建算法

3 實驗結果與分析

為了驗證KM-FNN算法的算法性能,在MATLAB 2013b 的實驗環境下針對不同的真實數據集下分別實現了提出的KM-FNN算法、LIN算法[9]、MR算法[9]和小波神經網絡(wavelet neural network,WNN)算法[16],并比較了實驗結果。

3.1 實驗數據集

①IBRL數據集

選取了由IBRL部署中的兩組節點的數據子集作為實驗對象。第一組數據子集(IBRL_1)包含的節點ID分別是1,2,3,4,6,7,10,33。第二組數據子集(IBRL_2)包含的節點ID分別是17,18,19,20,21,22,23。兩組數據集都對應于2004年2月28日至2004年3月7日九天內所收集的數據。

②LUCE數據集

LUCE數據集(洛桑城市冠層實驗)來自于2006年7月以來部署在洛桑聯邦理工學院內的無線傳感器網絡。該網絡共包含97個節點,根據節點之間的時空相關性分為10組傳感器節點集。在2006年10月1日到2007年5月9日期間,每個節點以31 s的采樣周期采集六種屬性數據,包括環境溫度、地表溫度、相對濕度、太陽輻射、土壤水分及風向。選取了LUCE數據集中的兩組節點的數據子集作為實驗對象,第一組數據子集(LUCE_1)包含的節點ID分別是10、14、15,17、18、19。第二組數據子集(LUCE_2)包含的節點ID分別是81、82、85、86、87、89。兩組數據子集都對應于2007年1月1日至2007年1月30日三十天內所收集的數據。

③JNSN數據集

JNSN數據集來自于江南大學智能感知與無損檢測實驗室部署在校園內的無線傳感器網絡系統。該系統由30個普通傳感器節點、匯聚節點、數據轉發設備和服務器構成。節點的分布參見圖5。

圖5 傳感器網絡節點部署圖

在2018年4月25日到2019年3月10日期間,每個傳感器節點以10 min的采樣周期采集三種屬性數據,包括環境溫度、相對濕度、光照強度。然后將感知數據通過匯聚節點匯總至無線自組網系統中,在終端服務器中調試算法以及分析數據。選取了JNSN數據集中的數據子集(JNSN_1)包含的節點ID分別是1、2、3、5、6、7,對應于2018年6月14日到2018年8月11日所收集的數據。

為了削減數據集,并保證訓練集中不存在缺失數據,以模擬節點部署初期的感知數據。針對來自IBRL_1,IBRL_1,LUCE_1,LUCE_2和JNSN_1的數據分別以4.5 min間隔、5 min間隔、70 s間隔,35 s間隔和27 min間隔重新采樣。采用溫度作為評估數據。表3列出了所使用的所有數據集。

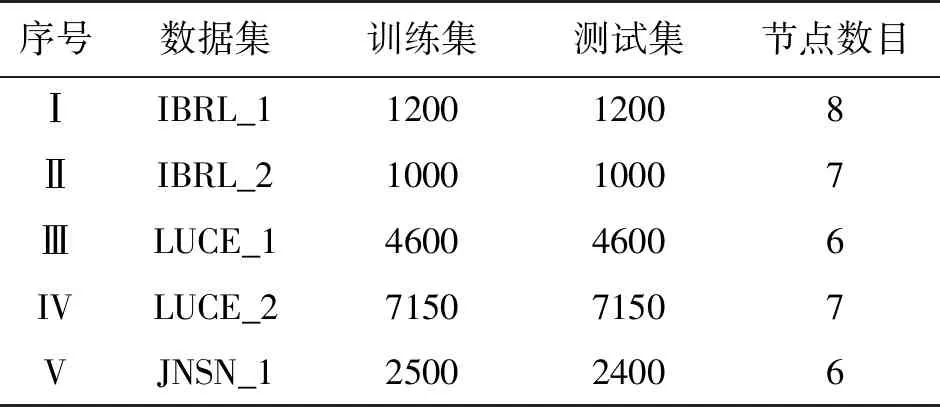
表3 實驗所用數據集

在數據集中查找是否出現缺失值,經過統計發現,在測試集中出現了不同程度的數據缺失,其缺失位置用NAN代替。表4表示實驗數據集中缺失數據的分布情況。

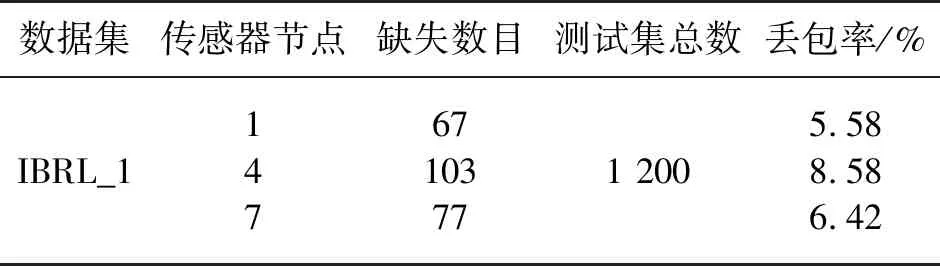
表4 數據集中缺失數據的分布情況(a)IBRL_1數據集

(b)IBRL_2數據集

(c)IUCE_1數據集

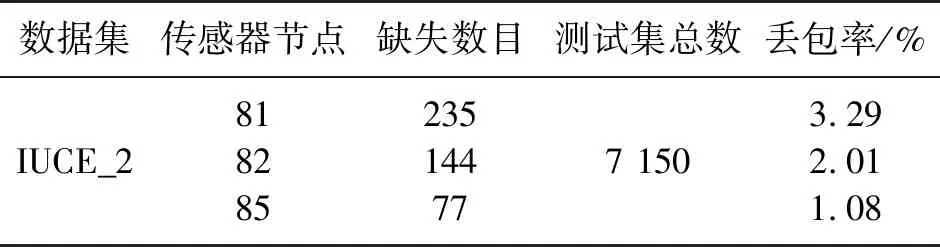
(d)IUCE_2數據集

(e)JNSN_1數據集

3.2 實驗結果

由于節點數據隨著時間的推移,其數據分布發生了較大的變化,KM算法將具有對應分布特征的節點數據分為k類,建立k個模型以滿足當前節點的分布規律。圖6(a)表示數據集I中1號節點于2004年3月1日內的完整數據。圖6(b)數據集I中1號節點于2004年3月1日至2004年3月3日三天內的完整數據。其中,設k值為4。

圖6中取k值為4。即數據根據其分布的特征規律劃分為4部分,劃分的邊界值分別為:第一類邊界[17.195 4,19.106 4],第二類邊界[19.243 6,21.438 8],第三類邊界[21.458 4,23.781 0],第四類邊界[23.820 2,26.133 0]。首先計算四類樣本的單個數據與類別中心數據的MSE值,然后計算四個類別的平均MSE,其大小為0.257 5。設k值為3并重復上述實驗,其大小為2.013 3;設k值為2,其大小為3.829 5。通過比較可知,當k取值為4時,數據分布的平均MSE值最小,這表明當前數據的分布較均衡。若取k值為5以上時,算法的復雜度過大,不合適真實場景的應用。因此,為了更好地重建缺失數據,故所有實驗均選擇k為4。

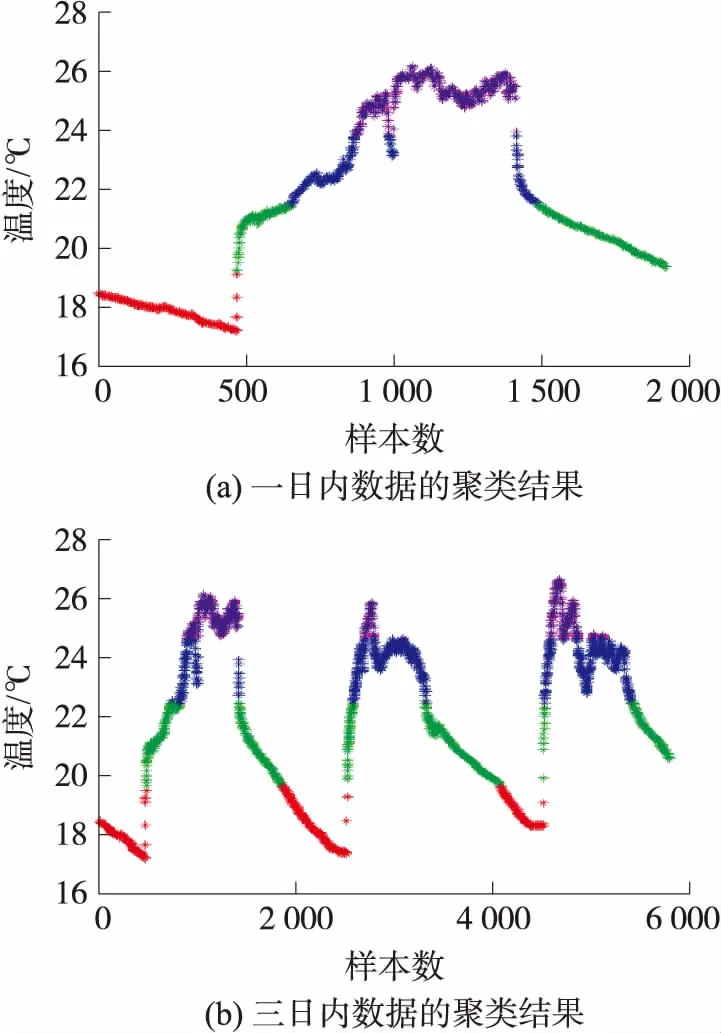
圖6 數據集I下1號節點數據的聚類示例

分別選擇IBRL_1下1號節點,IBRL_2下17號節點,IUCE_1下10號節點,IUCE_2下81號節點,JNSN_1下1號節點,JNSN_2下8號節點實施了3次對比實驗,并選取平均值作為最終數據,表5給出了各算法關于5個數據集的實驗結果。可以看出,CELM的平均均方誤差比WNN、LIN、MR分別減少了0.842,0.994,0.381。CELM的平均決定系數比WNN、LIN、MR分別提高了6.65%,5.94%,2.82%。

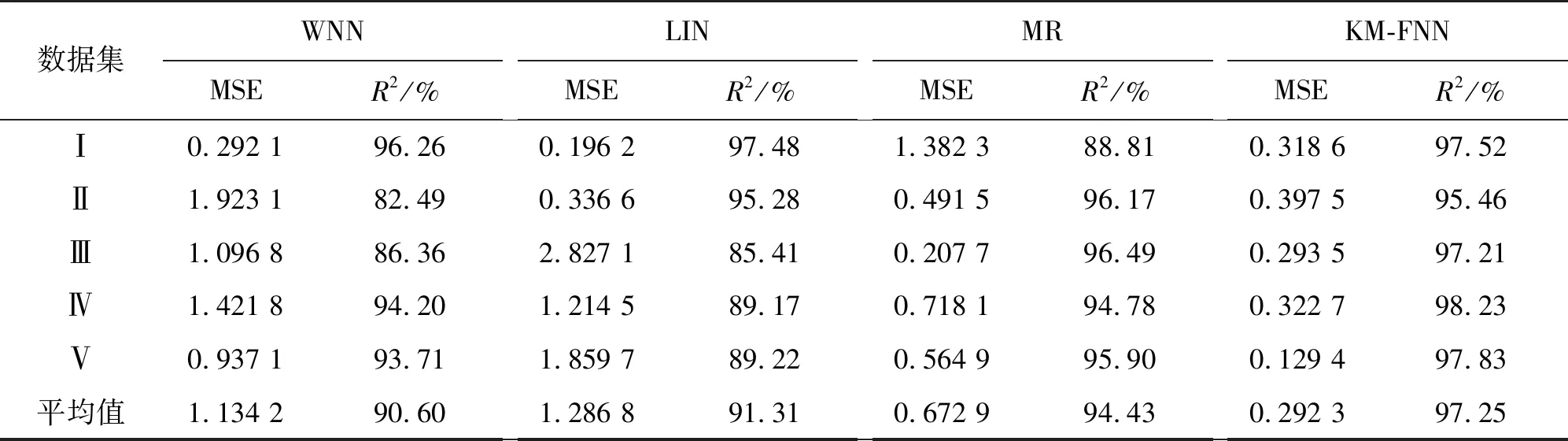
表5 四種算法的數據重建對比結果

為了驗證不同數量的缺失數據對實驗的影響,使用四種算法在數據集Ⅲ和Ⅴ下分別針對17號節點和7號節點的數據進行實驗。其中,在兩個節點數據的測試集隨機位置中分別刪去數量為10,20,30,40,50,60的數據。實驗結果見圖7。

圖7 四種算法的MSE對比實驗

由圖7可知,LIN的MSE最高,這是由于LIN是基于節點的時間相關性,其適應于較短時間間隔內的數據呈平穩變化的場景下,而所用的數據集經過二次采樣,更加大了時間間隔。因此,該方法針對17號節點和7號節點的數據重建精度最低。MR基于傳感器節點的空間相關性,對缺失數據的估計相對較為精準,具有良好的數據重建精度。相對于WNN算法,KM-FNN具有極強的自適應性能,因此其模型精度最高。

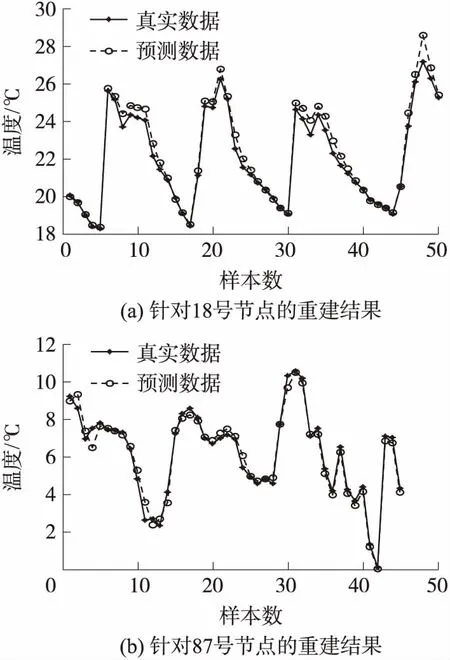
圖8 數據重建結果

圖8表示數據集Ⅱ下18號節點和數據集Ⅳ下87號節點的數據分別使用KM-FNN重建缺失數據的結果。其中,從18號節點和87號節點的數據集中分別刪去50個和45個樣本,以便人工模擬數據缺失情況。從圖中可以看出,真實數據曲線與預測數據曲線基本保持一致。綜上所述,KM-FNN具有精準的數據重建精度。

4 總結

針對無線傳感器網絡的數據缺失問題,提出了一種分簇式無線傳感器網絡缺失數據自適應重建算法KM-FNN。該算法使用模糊神經網絡模型重建節點的缺失數據,并引入滑動窗口機制與K-均值算法來模擬模型的自適應機制。仿真實驗表明,與以往同類算法相比,KM-FNN算法具有更好的缺失數據的重建性能,使用該算法避免了累積誤差對無線傳感器網絡數據的影響,從而有效地提高了數據的可靠性。由于真實環境中的簇頭節點的計算能力較低、能量有限。KM-FNN無法燒寫入簇頭節點中。今后將嘗試對KM-FNN進行優化,并將其應用于真實的WSN中,以驗證本算法的實用價值。