無線可充電傳感器網絡能耗分級充電策略*

吳寶瑜,萬 鵬,王高峰,程瑜華

(杭州電子科技大學電子信息學院,杭州 310018)

無線傳感器網絡是由大量具有傳感、數據處理和無線通信能力的傳感器節點組織成為的一個網絡結構[1]。網絡通過傳感器采集所需要的物理信息,發送給基站中心進行數據處理,進而傳輸給信息采集者。大部分的傳感器采用電池提供能量,為了傳感器網絡能夠持續有效地工作,必須定期地對電池進行更換,避免因電池能量耗盡后導致傳感器失效。但有些傳感器網絡的部署環境較惡劣,導致傳感器的電池更換不方便。在一些研究中,為延長無線傳感網的網絡壽命,對傳感器網絡采用更好的組網方式和能量均衡算法[2],盡可能地減少能量消耗,但這些方式只是減緩了能量耗盡的過程,并不能從根本上解決能量不足的問題。為應對這一問題,具有無線充電功能的傳感器網絡,即無線可充電傳感器網絡應運而生[3-5]。對于無線可充電傳感器網絡,當前采用的無線充電方式可分為靜態充電方式[6-7]和動態充電方式[8-14]兩種。對于靜態充電方式,可以看作充電源是固定不動的,傳感器接收來自固定充電源的電磁能量,但由于現有遠距離電磁輻射充電技術本身的局限性,很難克服因距離遠所帶來的能量傳輸衰減問題。隨著磁耦合諧振充電技術的快速發展,近距離快速高效地給傳感器無線充電技術越來越成熟[15-17]。通過配備高容量電池的移動小車移動至傳感器附近給傳感器充電的動態充電方式受到了很多人的關注。文獻[8]提出了一種移動充電小車的協作調度算法,該算法是一種時空計費調度算法,通過調整傳感器的充電優先順序,減少死亡節點的個數,來保證整個傳感器網絡的有效運行;文獻[9]提出在大規模無線傳感網中,根據不同傳感器節點的能量需求,優化充電小車的個數,盡可能地減少充電小車的數量使其達到最優;文獻[10]提出充電吞吐量的概念和一種新的充電范例,為移動充電小車找到最佳的充電閉合路徑,使其包括最多的傳感器節點數量,即小車在周期T的時間內,能夠給盡量多提出充電要求的節點進行充電。文獻[11]將小車的路徑規劃問題論述為一個旅行商問題TSP(Traveling Salesman Problem),并進行分析建模。文獻[12]基于充電小車能量有限的前提,將整個傳感器網絡分為不同的充電區域,充電小車通過給不同區域的傳感器進行充電,對整個傳感器網絡進行能量補充。文獻[13]結合傳感器網絡中的通信抗干擾技術和能量補給策略,對傳感器網絡進行分簇,由于簇頭節點能量消耗較大,先對簇頭節點進行能量補充,再對一般節點進行能量補充,能夠使得傳感器網絡更好地維持其生命周期。文獻[14]提出一種虛擬骨干網的移動能量補給策略,給特定骨干節點進行充電的方式補充能量消耗較大的傳感器節點。以上的動態充電算法規劃中,無論是增加充電小車的數量還是考慮時空關系,都是為了解決傳感器能耗特別大導致其生命周期很短,或者是傳感器網絡規模較大導致單個充電小車滿足不了充電需求的問題。但有研究表明,傳感器的能耗一般很低,傳感器的生命周期相對較長,對于充電時效性并無非常苛刻的要求,而且實際的傳感器網絡中傳感器的能耗值差異較大[18]。本文著重研究在傳感器網絡能耗分布不均的情況下,通過對傳感器能耗進行分級,結合蟻群算法[19]對路徑的計算,優化充電小車移動總路徑,從而減小充電小車的損耗,提高經濟性。

1 問題描述

1.1 模型建立

在一個L×L大小的二維空間中,部署了一個無線可充電傳感器網絡,其中包括N個無線可充電傳感器、一個移動無線充電小車、網絡中心位置的基站服務站。網絡模型如圖1所示。整個無線可充電傳感器網絡構成一個無向圖G=(V,E),V={v0,v1,v2,…vN}表示基站和傳感器集合,v0表示基站位置,vi表示傳感器位置,E表示傳感器兩兩之間的鏈路集合。

每個傳感器的能耗值各不相同,用Pi表示。在無線傳感器網絡中,無線傳感器的能量消耗功率Pi是與傳感器數據的發送量和接收量以及信息采集直接相關的,模型如圖2所示[11]。

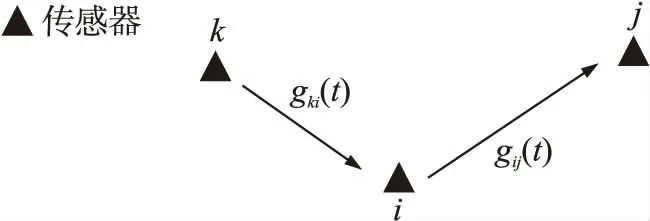
圖2 傳感器能量消耗模型

圖2中,假設在t時刻,i傳感器向j傳感器發送數據的速率為gij(t)bit/s,發送數據的功率因子為Cij,單位為J/bit,那么對于節點i來說,t時刻用于發送數據的功率Ps(t)由式(1)表示,同樣的在t時刻,節點i接收k節點發送來的數據的速率為gki(t)bit/s,相應的功率因子為ρ,單位為J/bit,那么在t時刻接收數據的功率Pr(t)由式(2)表示,Pc(t)為傳感器采集信息的能量消耗功率,則在t時刻,i傳感器的能量消耗功率Pi(t)由式(3)表示:

(1)

(2)

Pw(t)=Ps(t)+Pr(t)+Pc(t)

(3)

從上文的傳感器能量消耗模型可知,每個傳感器由于發送與接收數據量并不都是一致的,會產生不同的能量消耗率,則每個傳感器的能量狀態都是不同的,具有不同的能量補充需求。

為避免傳感器能量耗盡導致網絡失效,充電小車需定時地給網絡中能量小于閾值ETH的傳感器進行一對一的能量補充。若用ES表示傳感器當前電池容量,則傳感器生命周期為Ti,易得Ti=(ES-ETH)/Pi。傳統的傳感器網絡小車充電方式為遍歷全部的傳感器節點,根據實際的需求進行選擇性充電。但考慮到實際傳感器網絡中傳感器能耗值的差異,可選擇能耗值相近的傳感器作為一個集合,將整個傳感器網絡分為若干個包含不同能耗級別傳感器的集合,充電小車每次給不同傳感器節點集合進行充電。圖3為充電小車給某一能耗級的傳感器充電的示意圖。

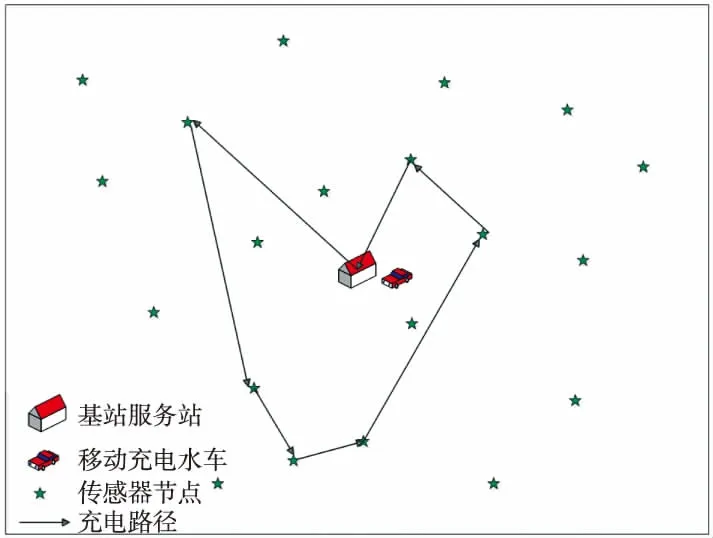
圖3 小車給某一能耗級傳感器充電示意圖

1.2 問題定義

我們研究的問題為一個充電小車周期性充電問題:在一個周期性的時間T內,根據傳感器能量的需求,分不同的輪數給傳感器進行能量補充,直至能量需求最小的傳感器節點都被補充過一遍能量。其中充電周期T的定義由式(4)得到。

T=Tp+Tvac+Tc

(4)

式中:TP表示小車充電中移動消耗的總時間;Tvac表示充電小車停靠在服務站時間;Tc表示停留在傳感器節點充電的時間,優化的目標為最大化駐站時間比Tvac/T。文獻[11]證明了最大化駐站時間比就是最小化移動時間,假定充電小車的移動速度是一定的,忽略充電時間,則最終就是優化移動路徑使其最小的問題。總移動路徑用LTSP來代替,那么問題就轉化為TSP問題[20],即小車在對傳感器節點進行充電過程的路徑規劃問題,式(4)轉變為式(5):

T=TTSP+Tvac+Tc

(5)

式中:TTSP為充電小車在充電過程中移動的時間。于是,在一個充電周期內,保證每個傳感器節點都能夠得到能量補充的情況下。由于充電小車并不是一次性遍歷完所有的傳感器節點,因此每一次遍歷的過程都可看作一個TSP問題,總移動路徑即為每次遍歷路徑的總和。最小化充電小車的移動總路徑LTSP成為主要優化目標。

在小車移動時間TTSP內,傳感器也會進行能量消耗的過程。為了保證沒有傳感器出現能量耗盡的情況,將前文的能量閾值ETH的確定進行充電約束,即保證在小車移動時間內,每個傳感器的能量閾值生命周期能夠大于總充電移動時間。如式(6)所示:

ETH/Pi>TTSP

(6)

2 算法分析和設計

2.1 算法思想

充電小車對傳感器網絡進行路徑規劃的傳統算法優化中,小車通常會一次性遍歷所有傳感器節點,進而根據節點的充電需求決定是否對節點進行能量補充,這種按需充電的方式會大大增加小車不必要的移動能量消耗。而在實際的傳感器網絡中,能耗分布是很不均衡的。基于此,在相同的時間周期內(即所有傳感器節點都補充過一遍能量的時間內),將能量補充路徑分成多個部分進行,可使得小車遍歷路徑值有較優的計算結果。根據傳感器網絡的各傳感器的能耗差異,給傳感器網絡分為能耗級別不同的集合,基于此,本文提出非固定周期算法和固定周期轉移算法兩種算法。對于非固定周期算法,充電小車根據每個能耗級別中傳感器最小的周期進行充電,充電小車每次出動的時間間隔是不固定的。針對非固定周期算法出動頻數較多的劣勢,進一步提出一種固定周期算法,充電小車每次出動的時間是固定的。本文在固定周期算法中,又創新性地提出了將部分能耗級別低的傳感器向能耗高級別高的傳感器集合轉移的優化算法,稱為固定周期轉移算法,優化總充電小車遍歷路徑值。

2.2 算法設計

2.2.1 能耗分級

給定傳感器集合V之后,給出對應每個傳感器的能耗值Pi,則每個傳感器的生命周期Ti=(ES-ETH)/Pi,找出其中最大值Tmax和最小值Tmin,計算(Tmax-Tmin)/Tmin的值,并向上取整可得待充電的傳感器集合的分級數,記為k。由此可得能耗分級后的傳感器集合VV={VV1,VV2,…,VVk},VVk表示集合V中生命周期值在kTmin和(k+1)Tmin之間的傳感器節點。

2.2.2 非固定周期算法

在進行能耗分級之后,找出網絡中具有最小剩余生命周期傳感節點所在的能耗級,充電小車對此能耗級中的所有傳感器采用蟻群算法[19]進行充電路徑計算。第i個傳感節點的剩余生命周期定義為(Ei-ETH)/Pi,其中Ei為能耗級中第i個傳感節點的剩余電池能量。在充電小車完成一次充電后,算法將更新網絡中各傳感節點的剩余生命周期,并重新尋找具有最小剩余生命周期傳感節點的能耗級,然后進行充電。算法過程描述如下:

輸入:{v0,v1,v2,…vN},Pi,ES

輸出:LTSP

①根據(ES-ETH)/Pi計算生命周期;

②計算(Tmax-Tmin)/Tmin的值,并向上取整,求得能耗分級數k,以及相應的能耗分級后的傳感器集合VV={VV1,VV2,…VVk};

③根據(Ei-ETH)/Pi求得每個傳感節點的剩余生命周期;

④找出具有最小剩余生命周期傳感節點的能耗級VVi并給其中的傳感器充電;

⑤用蟻群算法ACATSP(VVi)計算每次充電路徑值;

⑥重復步驟③,④,⑤直至全部的節點都被補充過一遍能量;

⑦求小車總遍歷路徑LTSP=∑ACATSP(VVi)

算法中每次選取的VVi是根據具體能耗級的最小剩余生命周期確定的。從能耗級最低的VV1開始,直到能耗級最高的VVk被充電的過程中,有些VVi可能被多次充電,即出現充電小車的出動次數較多,導致充電移動資源浪費的問題。為減小這種移動資源的浪費,提出了固定周期轉移算法,進一步優化小車總移動路徑。

2.2.3 固定周期轉移算法

第1階段算法描述如下:

輸入:{v0,v1,v2,…vN},Pi,ES

輸出:LTSP

①根據(ES-ETH)/Pi計算生命周期;

②計算(Tmax-Tmin)/Tmin的值,并向上取整,求得能耗分級數k,以及相應的能耗分級后的傳感器集合VV={VV1,VV2,…,VVk};

③求得小車每次遍歷的集合VX={VX1,VX2,…,VXk};

第2階段:遍歷一遍VX集合中的各個VV變量,找出只出現一次的VV集合,假設有M個,按照VVi的下標值從小到大排列并依次由集合C′1,C′2,…,C′M來代替,隨后按下標從大到小地進行集合間傳感器節點轉移。具體過程如下:初始化i=1,將C′M中的傳感器元素每次轉移i個到C′M-1中,每轉移一次,計算一次遍歷的總路徑值LTSP,將路徑值減小的轉移節點記錄下來;令i=i+1,在路徑值減小的轉移節點中每次轉移i個到C′M-1中,同樣計算每次遍歷的總路徑值;這樣,直到找到最小路徑值對應的最優轉移節點及個數。

然后對C′M-1和C′M-2進行上述類似的轉移過程,直至得到最優路徑下的最優轉移節點及個數;最后,直到完成C′2到C′1的轉移過程。取最優的轉移組合以及在這個轉移組合下的最優轉移節點,將此時的最優路徑數LTSP作為最終算法優化后的路徑數。

第2階段算法描述如下:

輸入:VX

輸出:LTSP

①找出VX集合中只出現一次的VV變量,個數記為M;將每個變量值從小到大排序并由C′1,C′2,…,C′M代替;

②初始化i=1,將C′M中的元素每次i個轉移到C′M-1中,每轉移一次計算一次LTSP值,記錄路徑值減小的轉移節點;

③令i=i+1,從路徑減小的元素里每次轉移i個節點,直到找出最小路徑值下的最優節點轉移數;

④對C′M-1和C′M-2重復步驟2和步驟3的過程,得到最優節點轉移數,直到計算完C′2和C′1;

⑤對比每個轉移組合下的路徑值,選取最優轉移組合下的轉移節點數;

⑥更新VX集合,得到此集合下最小值LTSP。

這里要說明的一點是,倘若經過第2階段算法的轉移規則之后,并不能使小車的路徑數有所減少,不進行第2階段的轉移過程。

為了便于理解第2階段的轉移過程,下面用一個具體的例子來說明節點轉移算法的轉移過程:

無線可充電傳感器網絡中有一個位于中心的基站服務站和10個傳感器節點v1～v10,根據能耗值的不同,將整個傳感器網絡分成了3個能耗級別VV1,VV2,VV3。3個能耗級別所對應的充電周期為T,2T,3T,于是對于充電小車每次遍歷的路徑集合分別為VX1=VV1,VX2=VV1∪VV2,VX3=VV1∪VV3,如圖4所示為不同能耗級傳感器集合,圖5(a)～(c)為一個周期內總共3次不同的遍歷路徑示意圖。

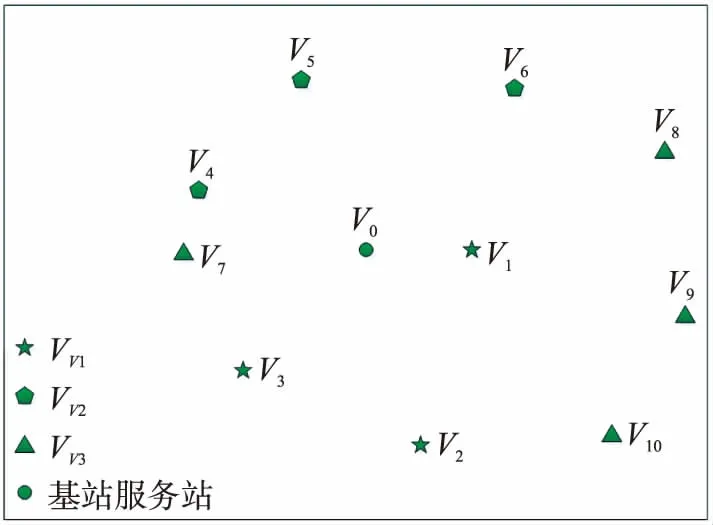
圖4 不同能耗分級圖

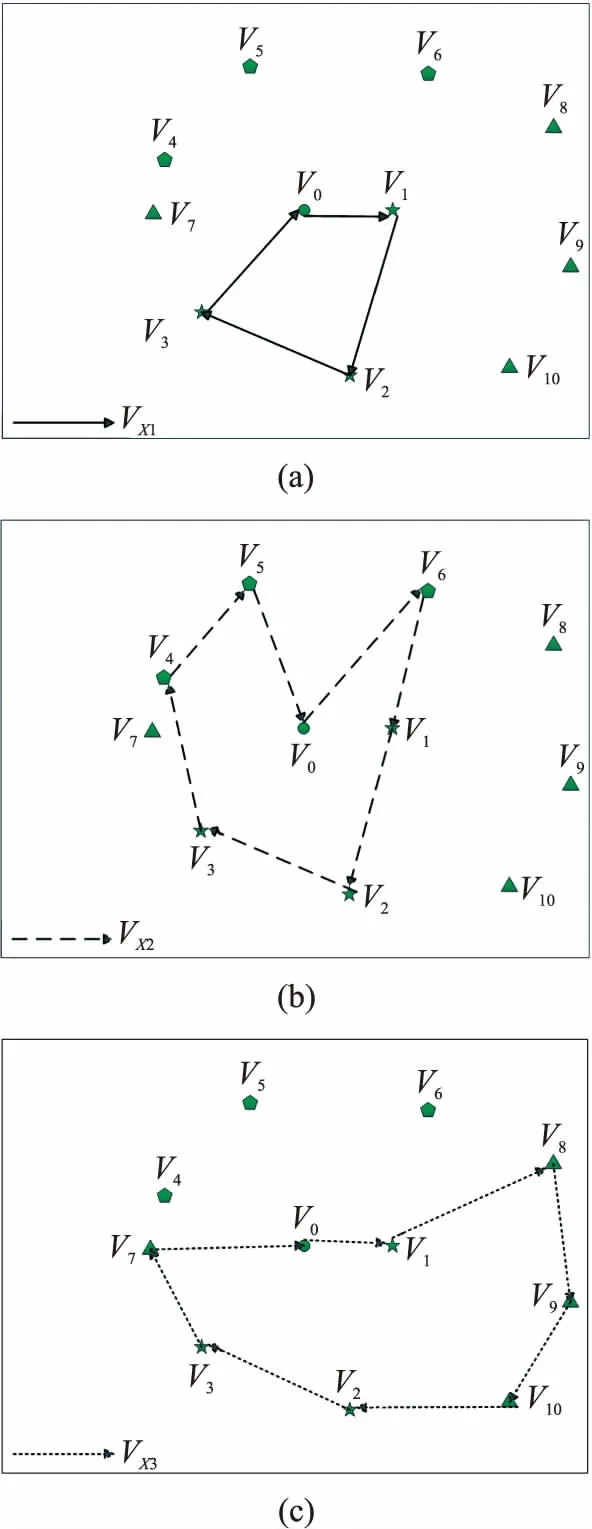
圖5 小車充電遍歷路線示意圖

圖6(a)～(c)為進行第2階段算法的轉移規則之后得到的路徑遍歷示意圖。轉移之后的節點,由于能耗小于集合中其他的傳感器節點,即生命周期大于其他的節點,則不影響其本身的能量補充過程。從圖中可以看出,由于v7特別靠近v3v4,將原屬于VV3的v7節點轉移到VV2中,可以減小路徑值。圖5(a)和圖6(a)路徑相同,圖5(b)和圖6(b)差距很小,轉移前與轉移后的路徑值主要為圖5(c)和圖6(c)的大小比較,很明顯后者較小,即轉移后的路徑值會變小。當傳感器節點數較多時,可以使用節點轉移規則找出最適合的轉移方式。

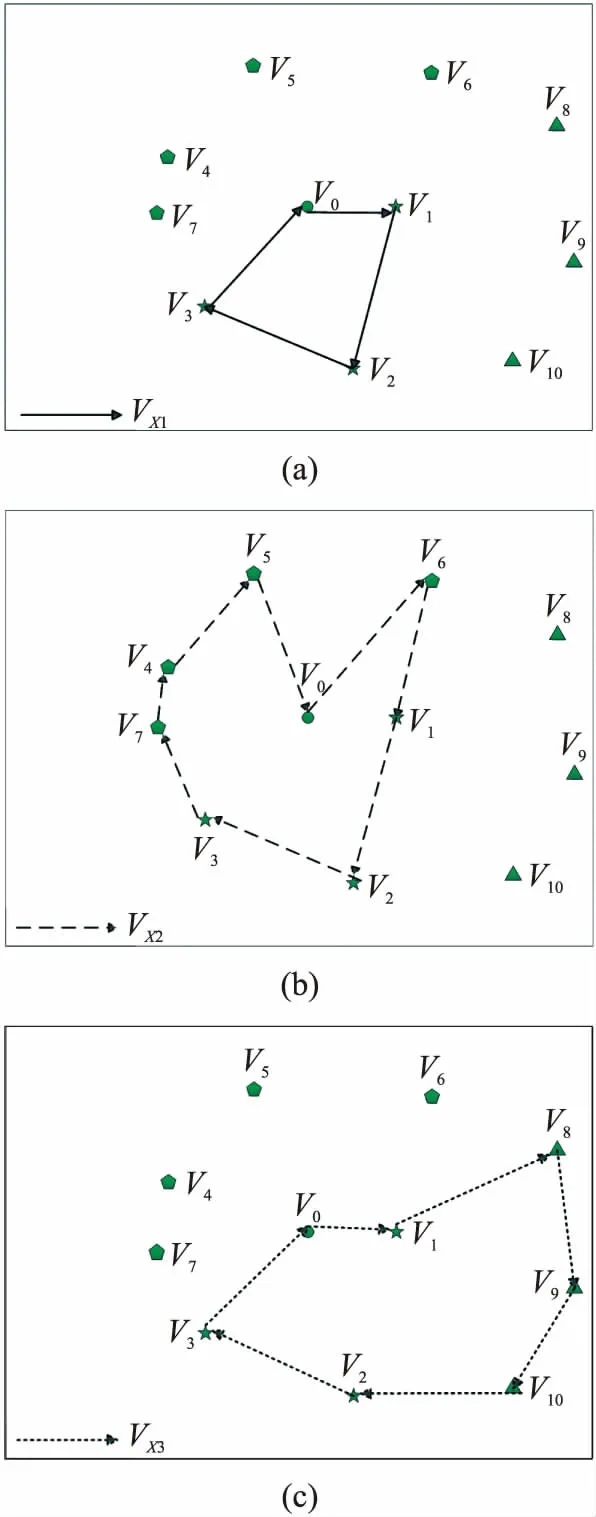
圖6 轉移節點后小車充電遍歷路線示意圖

2.3 算法復雜度分析

本文研究的問題本質是一個NP-hard問題。能耗分級階段,主要是根據能耗進行分類,只要計算完傳感器節點的個數即可,算法時間復雜度為O(1)。在求解TSP問題階段,時間復雜度很大,采用蟻群算法,能夠較好地解決TSP問題,但是算法的復雜度并沒有降低,其復雜度為O(2n·n2)[20]。但是在此過程中由于采用了分級策略,減小了每次的n值,能夠減小算法的計算量。在節點轉移過程中,只考慮上一級向下一級逐級轉移的節點轉移方式,由于是k級的能耗分級,規則定義可轉移所有節點,則所需的時間復雜度為O(n2)。

3 仿真實驗與結果分析

為驗證本文所提出的非固定周期算法和固定周期轉移算法的有效性,這里將它們與傳統周期遍歷算法[14]進行了比較。參照文獻[14]中對傳感器網絡中的參數設置,將傳感器網絡布置在1 000 m×1 000 m 大小的正方形區域內,傳感器的電池容量為10 kJ,基站服務站的位置和小車的初始位置為中心位置,坐標為(500 m,500 m)。在仿真的過程中,通過改變傳感器的個數,傳感器的能耗值范圍,比較算法的路徑值。

在上文中的多種傳感器個數以及能耗范圍設置下的仿真實驗中,由于TSP問題的復雜度與傳感器個數n相關,考慮到計算量,這里選取了一組能耗級別為3級,傳感器個數為20的路徑遍歷仿真結果。

圖7為傳統周期遍歷算法小車充電路徑圖。

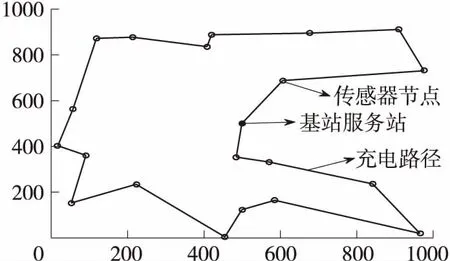
圖7 傳統周期遍歷算法路徑圖

圖8(a)～(c)為非固定周期算法小車充電路徑圖。

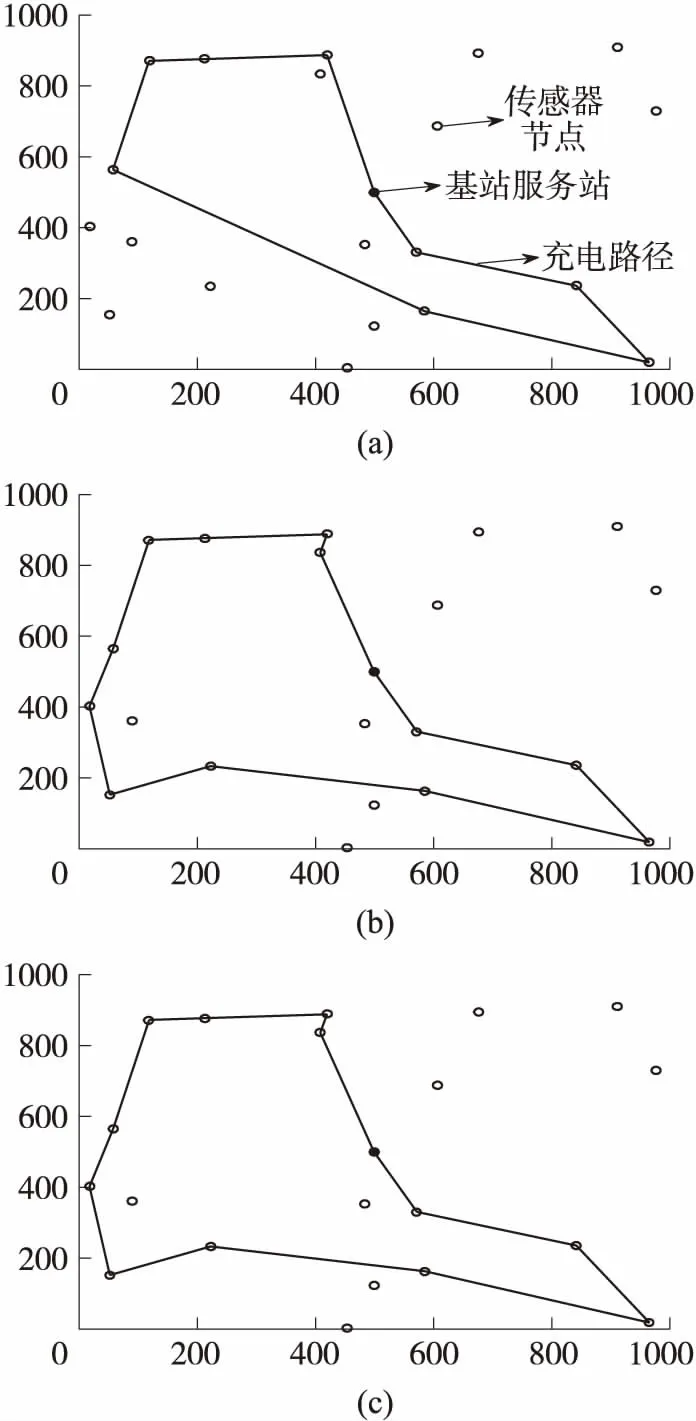
圖8 非固定周期算法充電路徑圖

圖9(a)～(c)為固定周期轉移算法小車充電路徑圖。

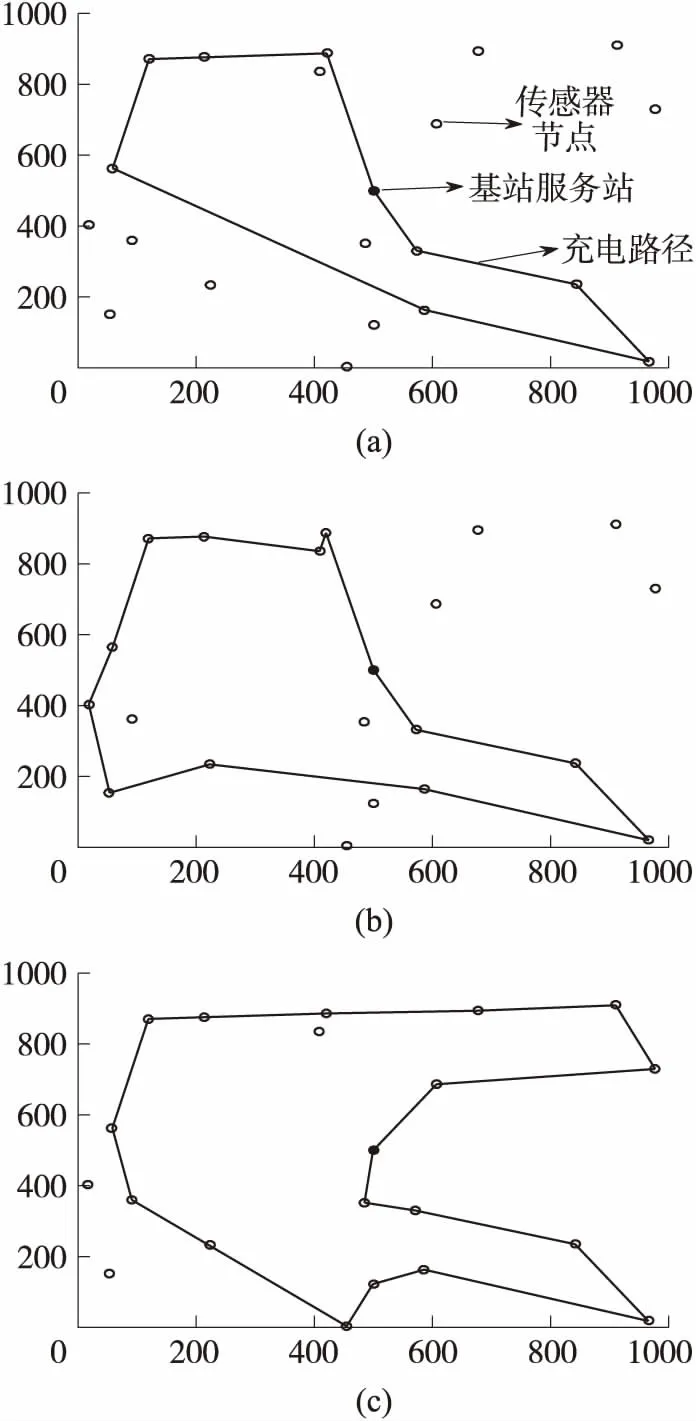
圖9 固定周期轉移算法充電路徑圖

由圖7、圖8和圖9可以看出,固定周期轉移算法在一個周期T內只需要出動3次,總的路徑值最少;傳統周期遍歷算法也出動3次,但每次遍歷所有傳感器節點,所以路徑值最多;非固定周期算法每次遍歷傳感器的路徑值較少。由于非固定周期算法的特點,圖8(a)的移動方式需要2次的充電過程,加上(b)、(c)各1次,小車總的出動頻數為4次,計算得到的總路徑值比固定周期算法得到的總路徑值多。

圖10和圖11進一步給出了在不同傳感器數量、不同能耗分級下算法的有效性。圖10為各節點能耗在0.1 J/s～0.3 J/s(對應能耗分級為3級)范圍內隨機取值,三種算法在傳感器個數為20,25,30,35時,相同時間內(由于傳感器最小能耗都為0.1 J/s,則每個傳感網絡的生命周期都相同)小車遍歷的充電路徑值。圖11為在保證傳感器網絡的個數為30時,在0.1 J/s～0.3 J/s,0.075 J/s～0.3 J/s,0.06 J/s～0.3 J/s,0.05 J/s～0.3 J/s(分別對應能耗分級為3級,4級,5級,6級)四種能耗分布下(每個傳感器網絡的最小能耗都不同,則每個傳感器網絡都具有不同的生命周期)三種算法小車遍歷的充電路徑值。從圖10和圖11可以看出,本文提出的2種算法都要比傳統的算法的路徑值要小。

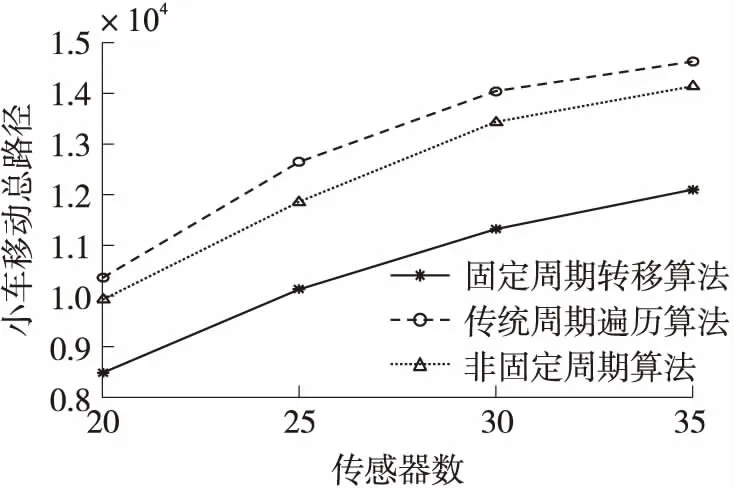
圖10 小車總路徑與傳感器數圖

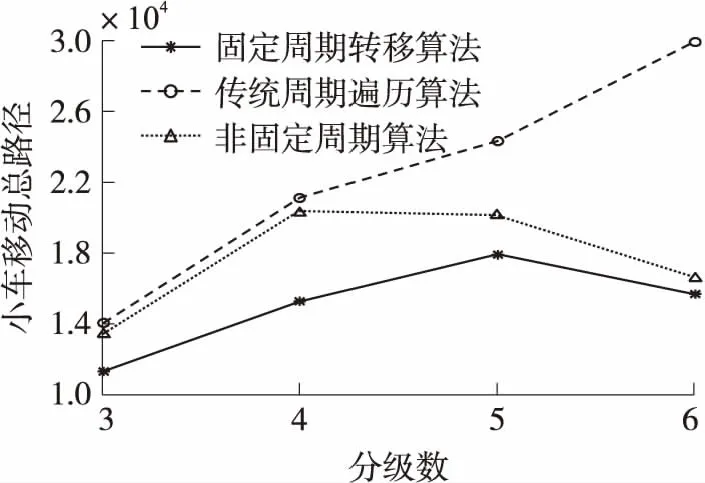
圖11 小車總路徑與分級數圖

圖12給出了3種算法在不同能耗分級數下小車出動頻數的比較,可以看到,在相同的時間周期內,固定周期轉移算法與傳統周期遍歷算法的出動頻數是一樣的,出動頻數都為能耗級數的值,而非固定周期算法的小車出動頻數較多,隨著能耗分級的增加,次數增加更加明顯。

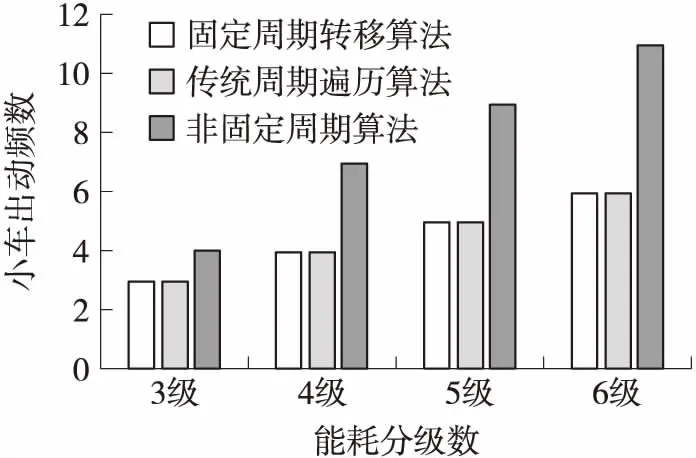
圖12 小車出動頻數比較圖

固定周期轉移算法在相同的周期時間內,小車遍歷的路徑值是最少的;傳統周期遍歷算法由于要遍歷全部的傳感器節點,必然浪費了大量的移動能量消耗;非固定周期算法由于較多的出動頻數,即使每次遍歷節點較少,相對于固定周期轉移算法,同樣會增加不必要的移動能量消耗。綜上所述,固定周期轉移算法無論在充電移動總路徑上,還是小車出動頻數上,較其他兩種算法都具有優勢。

4 結束語

本文基于無線可充電傳感器網絡的能耗差異,提出兩種能耗分級的充電規劃算法。一種是非固定周期算法,另一種是結合節點轉移規則得到的固定周期轉移算法。與傳統的周期性小車充電算法不同,兩種算法能夠根據傳感器網絡的能耗狀態,給傳感器網絡分級充電。在與傳統算法比較的過程中,在相同的參數條件下,能夠減小充電小車遍歷路徑值。其中,固定周期轉移算法能夠得到更小的路徑值。仿真結果表明算法在求解最優路徑值上的優異性能。在以后的研究中,可以尋找最優的能耗分級數以及更有效的節點轉移方法,進一步優化遍歷路徑值。