基于小波包分析的電機滾動軸承故障診斷

(貴州大學 電氣工程學院，貴州 貴陽 550025)

電機是現代工業過程中重要的驅動設備，在電動汽車領域也起到舉足輕重的作用，并且電機出現故障時會造成經濟損失，還可能危及人員的安全，所以其穩定性和可靠性尤為重要。電機故障的預測和診斷得到了越來越多的關注[1]。文獻[2]列舉了電機各類故障發生的概率，其中軸承故障發生的概率是最高的，占40%～50%。因此，對滾動軸承的故障診斷尤為重要。在傳統的信號提取處理方法中，傅里葉變換是最重要的工具之一，但對于非平穩、非線性信號，傅里葉變換卻不適用，存在一定的局限性。

小波分析適合非平穩信號，但是在信號高頻段部分是不再進行分解的，而在振動信號的高中頻段存在滾動軸承故障的大量故障特征信息，因此分解的精度不夠。小波包分析則克服了這一缺點，擁有更高的分辨率[3]。提出一種滾動軸承的故障特征信號提取的小波包分析方法，計算的特征頻率跟實驗結果能很好的對應，同時還介紹了選擇小波包分解層數的方法。

1 滾動軸承的結構

電機轉子轉軸與定子之間的連接部件滾動軸承的基本結構如圖1所示。主要由4個部分組成，首先是內外兩個同心圓環軌道，即軸承的外圈和內圈；其次是內外圈之間的滾動體；最后是具有銜接和固定作用的保持架[4]。其主要參數有：軸承節徑D、滾動體直徑d、內圈滾道半徑R1、外圈滾道半徑R2、滾動體的個數n、接觸角α。

在實際運行條件下，滾動軸承因其自身的結構特點、惡劣的環境和負載不平衡等原因，軸承故障在電機故障中出現的概率是最高的。

圖1 滾動軸承結構圖

2 小波包分析理論

2.1 小波包分析基本原理

小波包分析[5]是小波分析的延伸，其對信號的分析與重構更加細致,可在全頻帶對信號進行多層次的頻帶分解,頻率空間和時域空間被越分越細,則能更好地對信號進行頻帶分離,然后根據信號故障特征頻率區間提取相應的頻帶信號,再進行故障診斷,這樣減少了其他頻率成分的干擾[6]。三層的小波包樹形分解圖[5]如圖2所示，小波包分解具有如下關系:

S=AAA3+DAA3+ADA3+DDA3+AAD3+DAD3+

ADD3+DAD3+ADD3+DDD3

小波包分解與小波包重構[7]公式分別為

(1)

(2)

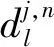
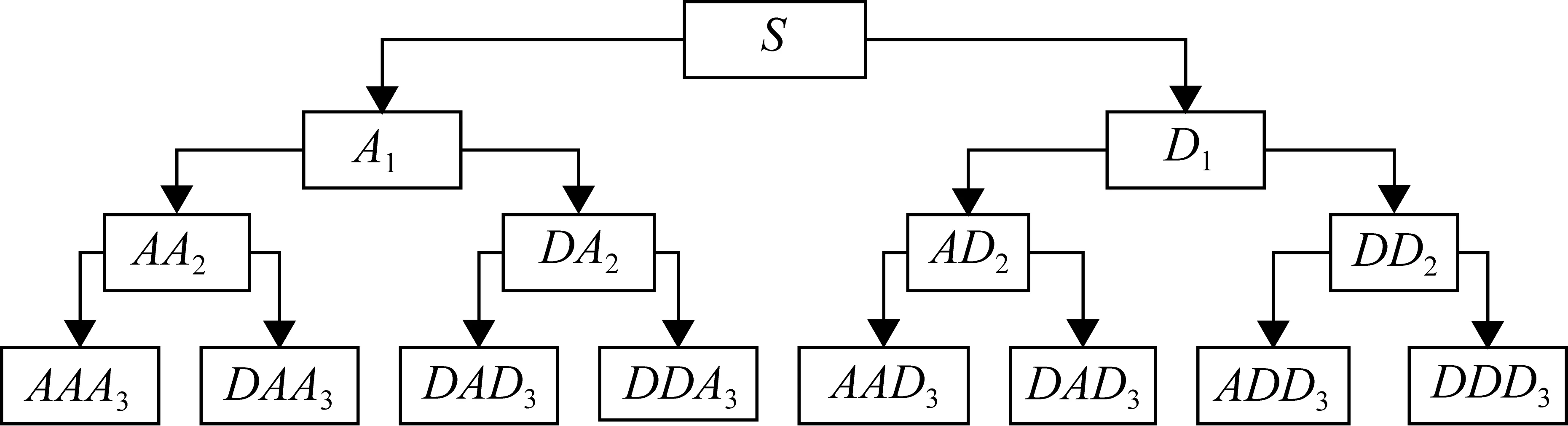
圖2 三層小波包分解過程

2.2 小波基與小波包分解層數的選擇

在故障特征提取領域，通常采用 Daubechies小波作為小波基，選取小波基為db2。

小波包的分解層數在提取滾動軸承故障特征時起到關鍵性的作用，當小波包分解層數過低，則不能精確地提取出軸承特性信息，會造成故障診斷的不精確。若增加分解層數，對軸承故障振動信號的分析是更加精細，但是提取出的特征維數會變大，分解后的信號數量有相應的增加，這會影響故障識別的速度以及準確度。所以要結合信號自身的特點來選擇小波包層數，并根據實際情況綜合考慮。文獻[8]給出了選取最佳分解層數范圍應該滿足的條件，公式如下：

(3)

式中，J為最大的分解層數；fs為采樣頻率；f為信號頻率。

2.3 故障特征頻率計算與小波包故障診斷流程

根據文獻[9]，測試滾動軸承型號為6250-2RS，其滾珠接觸角α=0°，滾珠個數為9，軸承節徑為1.537 in，滾珠直徑為0.3126 in。根據文獻[10]，式(3)中的信號特征頻率f就應該是故障特征頻率。記fvb為滾動體故障特征頻率、記fvi為內圈故障特征頻率，記fvo為外圈故障特征頻率，它們的計算公式分別為

(4)

(5)

(6)

式中，D為軸承節徑；d為滾珠直徑；α為滾珠接觸角；n為滾珠個數；fr為轉頻。對于內外圈軸承故障，文獻[11]給出了大約計算式：

(7)

在Case Western Reserve University的軸承數據庫中，選取負載為2 Hp，故障直徑為0.007 in，電機轉速為1750 r/min ，采樣頻率fs=12000 Hz，按前面相應的計算公式可得出滾動體故障、內圈故障、外圈故障的頻率及其倍頻，fvb=68.7 Hz，fvi=158 Hz，fvo=104.6 Hz。

對電機軸承故障信號的采集，并用小波包進行分析處理，通過計算理論的故障值與仿真結果的對比，從而實現滾動軸承工作狀態的識別。滾動軸承故障診斷流程圖如圖3所示。

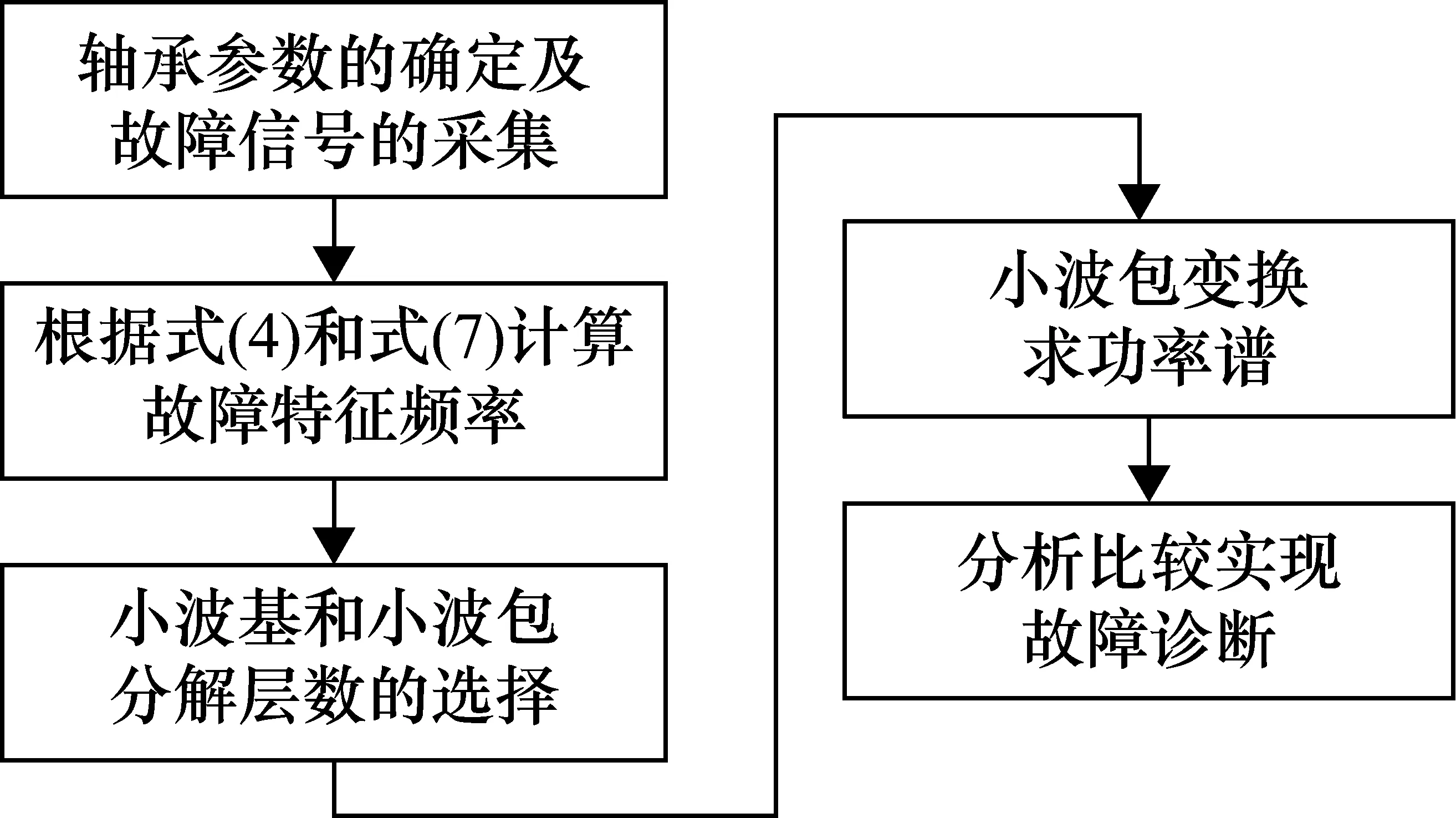
圖3 滾動軸承故障診斷流程

3 仿真與分析

軸承的轉速變化范圍為1730～1797 r/min，根據式(4)和式(7)計算可得：

由式(3)可以計算出最佳小波層數J≤5。當J=5時，特征向量維數為32，可能存在維數過大的缺點。當J=3時，特征向量維數為8，但軸承故障特征無法被精確地提取出。所以本文選取的J=4，特征向量維數為16。

正常信號和3種典型故障信號的功率頻譜圖如圖4所示，把正常信號和故障信號功率譜做比較，可以看出有故障的存在，故障特征頻率能夠隱約看出，但是不明顯，只知道軸承已有局部損傷故障發生，損傷部位無法確認。

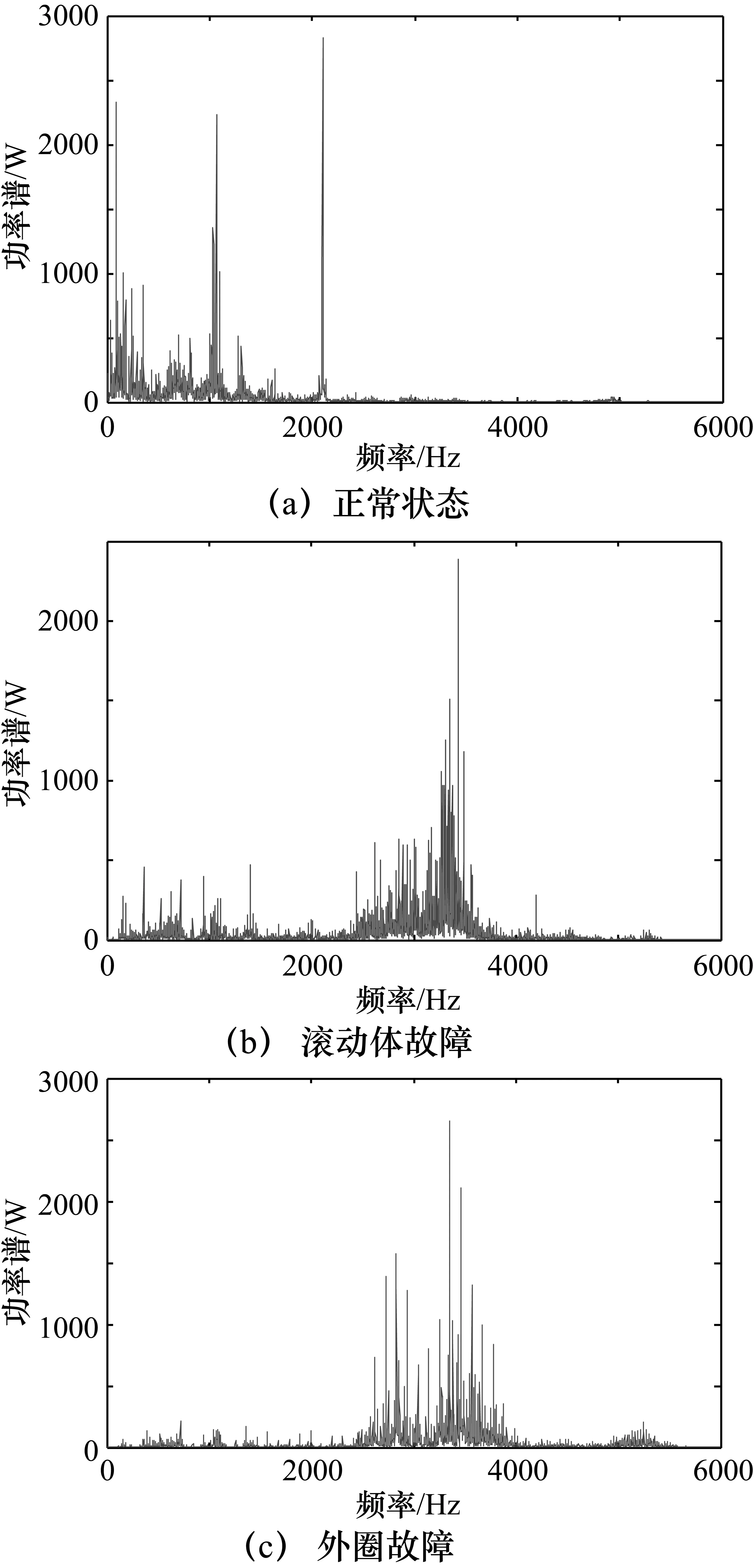
圖4 正常信號和3種故障信號的功率頻譜圖

為此，對其用Matlab編程后分別對1750 r/min轉速下3種故障信號進行4層db2小波包分解，為了提取故障特征頻率，首先重構了低頻信號，然后計算功率譜，結果如圖5所示。前面通過計算已經得到：fvb=68.7 Hz,fvi=158 Hz,fvo=104.6 Hz，及其倍頻，在圖中可以很明顯發現各類故障特征頻率的存在。

圖5 小波分解低頻段信號的功率譜

在小波分解低頻段信號計算功率譜之后，比較正常信號和滾動體故障信號的功率譜，如圖6所示，在圖中可以很明顯看出波形的不同，在特征頻率為68.7 Hz處出現了故障，進一步說明了該方法的可行性和準確性。

4 結束語

針對滾動軸承振動信號非平穩的特點，利用小波包分析的獨特優勢來提取故障特征，并給出該方法具體實現的流程。介紹了根據滾動軸承的故障特征頻率，計算得到小波包分解層數的最佳范圍，從而避免盲目的選擇分解層數。對采集的各類故障信號進行小波包分解，為了提取故障特征頻率，重構了低頻段信號并得到功率譜圖，功率譜上的故障特征頻率與計算的故障特征頻率一一對應。因此基于小波包分析方法能夠很好地對滾動軸承的故障做出診斷，仿真結果證明了此方法的有效性，具有一定的實用價值。

圖6 小波分解低頻段正常信號和滾動體故障信號功率譜比較圖