改進型分批估計與自適應加權融合方法研究
(1.福建師范大學福清分校 圖書館,福建 福清 350300; 2.福建師范大學福清分校 電子與信息工程學院,福建 福清 350300)
目前,無線傳感網絡在智能家居中的應用越來越廣泛。而無線傳感網絡數據量測的準確性和可靠性是其正確應用的基礎。然而它依然存在著一些待解決的問題[1-2]。首先,在智能家居中,大量的傳感器節點部署于相對較小且半封閉式的空間內,進行數據收集、存儲處理、無線傳輸等。在該監測區域內,區域溫度和壓力變化較大,易受電器輻射和噪聲干擾,使得傳感器采集數據讀數不準確,終端節點與協調器的無線數據傳輸不穩定、易丟失等,最終導致收集到不正確的數據。此外,在某些情況下,節點本身出現故障癱瘓,發出錯誤數據或成員節點直接失效,收集不到數據。其次,無線傳感網絡是自組織網絡,節點受空間覆蓋,時間校準的問題導致收集不正確的數據時有發生,特別是障礙較多的室內環境,信號覆蓋范圍受障礙影響大,易造成信號衰弱,影響數據可靠性。第三,小區域內的傳感器監測,空間位置相鄰,容易產生高度重復的相關性數據,該局部監測區域的大量數據傳輸顯得多余,占據了信道帶寬,浪費信道利用率,降低服務質量。第四,智能家居的某些應用中,用戶可能更關心的是監測結果,而原始數據的狀態并不那么重要[3],例如發生火災能夠迅速警報等。基于這種情況,仍然將各個節點的原始監測數據傳輸至協調器以及Sink節點,無法獲得更有用的信息,代價是傳輸大量數據,反而有可能因為信道競爭導致預警延遲。
為了解決上述問題,對多源傳感器數據進行預處理及有效的數據融合機制,修正偏差大的數據,刪除不可靠數據,去除冗余、融合高度重復的相關數據,是實現提高數據可靠性、精確性、降低冗余度的有效途徑之一。針對監測環境局部信息的一致性和變化緩慢的特點,文獻[4]提出了層次數據融合結構;對局部區域內采用加權數據融合狀態估計,然后基于支持度函數對來自不同局部區域內數據進行一致性分析,確保了信息的一致性和有效性。文獻[5]提出了一種基于三層架構的上下文感知、自我優化和自適應系統;最低層傳感器收集異構數據,中間層結合上下文信息利用動態貝葉斯原理處理測量數據的不準確性并推理估計,最高層通過采集傳感器集數據實現自由優化過程達到提高監測值的精度;結合卡爾曼濾波的優化貝葉斯估計也被用于改善多傳感器數據的不確定性和不一致性問題[6]。為了提高多傳感器測量的準確性,文獻[7]提出了一種基于偏好聚合形式的區間投票的方法;允許從狹窄的不確定性邊界內相鄰多傳感器獲得不準確的測量數據來確定測量參數的校正值,實現較好的測量準確度。針對各種傳感網絡模型中存在的錯誤、無用及冗余數據進行優化,引入模糊推理系統進行數據融合提高精確性和融合質量[8-9]。文獻[10]采用支持向量回歸機方法將各傳感器陣列數據進行融合以提高數據的準確性。文獻[11]提出了一種改進型分批估計的自適應加權融合算法,根據容許函數閾值剔除誤差較大的數據,利用改進型分批估計最優估計值,依據權值最優分配原則對每組傳感器數據進行組內自適應加權融合,從而計算精確值。本文在借鑒分批估計算法的基礎上,考慮受到環境因素影響造成監測偏差程度,提出了一種數據預處理與改進型分批估計加權融合相結合的算法。首先,該算法根據格羅貝斯準則一致性檢驗剔除疏失誤差數據;其次,引入環境因子改進分批估計算法計算當前最優監測值;最后,針對不同方位誤差分布不均勻特點,提出了權值最優分配原則實現自適應加權融合。
1 量測數據融合模型
無線傳感網絡終端節點數據采集完成后得到原始測量序列Xi={xi1,xi2,…,xik},k為每個傳感器周期內測量次數。量測數據融合過程如圖1所示。
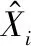
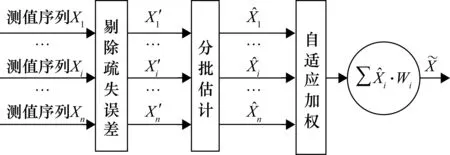
圖1 量測數據融合模型
2 量測數據預處理
實際測量中,必然存在著疏失誤差。智能家居安全監測中,利用帶有疏失誤差的量測結果判別預警結果是可靠的。因此,對于誤差偏大、錯誤的量測數據應該及時予以剔除,從而拒絕因疏失誤差而導致誤判的情況。采用格羅貝斯判據準則[12-13]進行數據一致性的檢驗。具體方法描述如下。
設某一傳感器節點i,某一采集周期內多次測量得到的量測序列為:Xi={xi1,xi2,…,xik}。其中,k為每個傳感器周期內測量次數。同時,設該原始數據服從正態分布,計算可得
(1)
(2)
(3)
根據順序統計原理,可知格羅貝斯統計量的確切分布。在給定顯著水平α后,通常取值為α=0.05或α=0.01,通過查表法找出格羅貝斯統計量的臨界值gi(k,α)。因此,由量測數據序列Xi服從正態分布,可知:
(4)
P[gij≥gi(k,α)]=α
(5)
3 改進型分批估計融合算法
完成了對疏失數據的剔除工作,得到具有一致性的量測數據序列。針對單傳感器的一致性量測序列,它們之間必然有著關聯性,具備高度重復性,這是其一。其二,對于單點傳感器以及整個系統而言,只需獲取一個監測結果。因此,對具有一致性量測數據序列進行監測值融合估計,高效地反映當前傳感器的狀態是很有必要的。對此,分批估計融合是一種簡單可靠的可行方案。但在實際測量使用過程中,傳感器測量受到復雜環境因素影響多變,可能存在均方差偏大的一致性檢驗數據,特別是與電子設備本身的電氣特性,以及不同方位受實時壞境,如輕微震動、受潮等諸多不可預期的因素有一定關系,因此通過引入環境因子來克服由此造成的誤差,即根據檢測區域環境的特點,選擇性地去除一定比例的最大最小值,有利于提高精確度,而傳統分批估計采用簡單算術均值計算在該方面具有一定的局限性。對此,依據順序統計理論和實踐經驗,去除部分最大最小值后的均值分析,顯得更加可靠和準確,更能夠反映數據的集中情況。
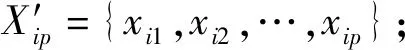
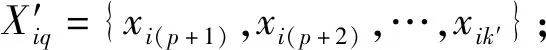
其中,兩組元素個數分別為p和q,且滿足p+q=k′。分別計算各組的算術平均值和方差,如下:
(6)
(7)
(8)
(9)
式中,ρ表示環境因子,指最優去除最大最小百分比。
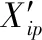
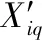
故此,根據文獻[2],利用分批估計理論可以求出該組傳感器量測數據序列最優融合監測估計值為
(10)
分批估計數據融合監測值的方差為
(11)
至此,考慮傳感器受惡劣因素影響導致量測值波動較大,通過引入環境因子ρ,對單個傳感器經一致性檢驗后的測量數據序列進行分批估計,給出了最優融合監測值及總方差。
4 自適應加權融合算法
盡管對于單傳感器數據測量準確性和可靠性提出了解決方案,然而,往往在局部區域內部署著多個同類型的傳感器節點,每個節點因方位、環境、噪聲干擾不同,感測值是不一樣的。因此,每個傳感器量測數據的準確性存在差異,量測誤差隨機性大,分布不均勻。那么,如何有效區別對待各個傳感器的數據差異,提高數據融合監測結果的可信度,是必然要解決的問題。本文采用權值最優分配原則,自適應加權融合,為每個傳感器數據自適應尋找其最優權值,使得總均方誤差最小,從而得到該監測目標的最優估計值[14-16]。自適應加權融合計算模型如圖2所示。
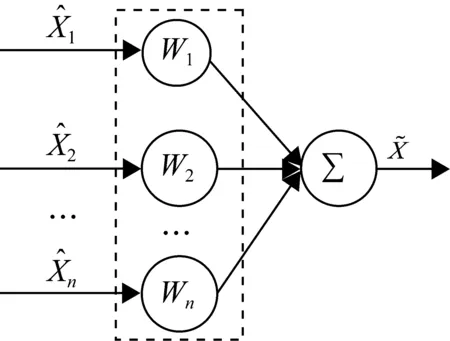
圖2 自適應加權融合計算模型
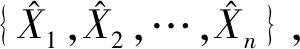
(12)
融合后的總均方差為
(13)
(14)
通過自適應權值分配,即可使得量測方差越大,獲得權值越低,否則相反。
5 實驗結果與分析
在火災監測狀態正常情況下,室內環境傳感器數據采集受環境因素干擾小且可能性較低,數據測量表現較為穩定;若有火情發生或處于萌芽階段,室內環境監測區域環境變化迅速多樣且復雜,對傳感器自身及其測量產生不利影響,造成測量數據偏差相對較大。為此,提出了一種數據預處理與基于環境因子的改進型分批估計相結合的方法。與此同時,該環境下,不同方位受影響程度不同,呈現出測量數據分布不均勻等特點,本文提出了綜合評價多傳感器測量數據,自適應加權融合方法,使得測量方差越大,獲得權值越低。
5.1 算法時間復雜度分析
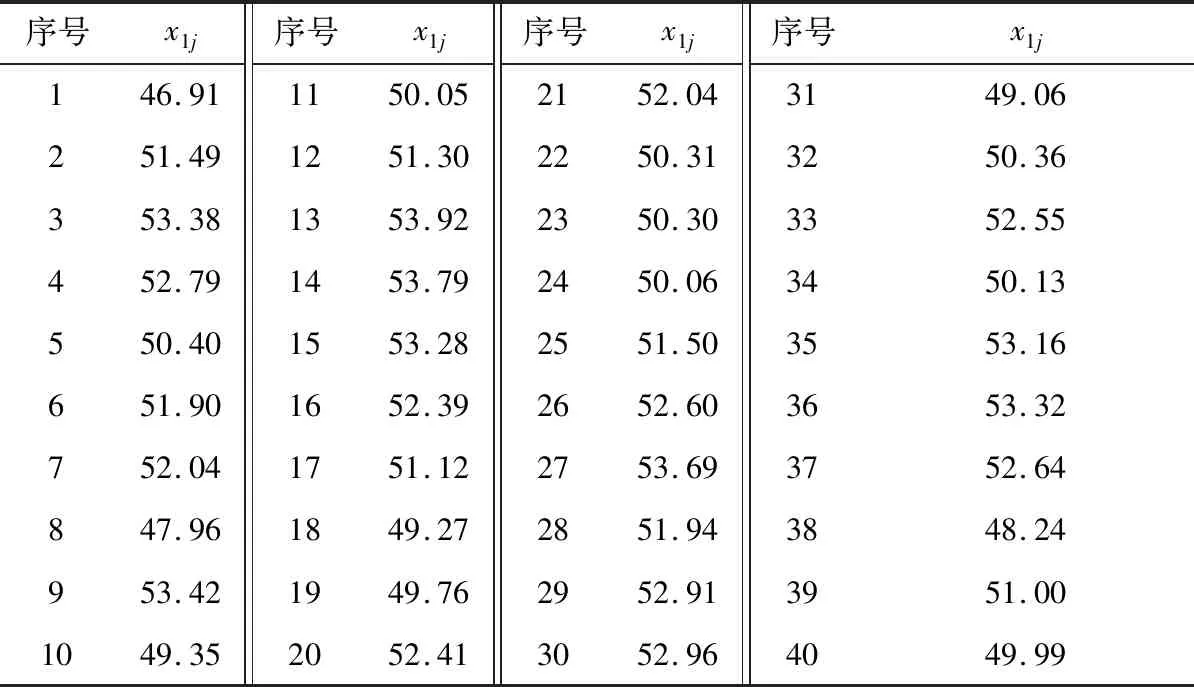
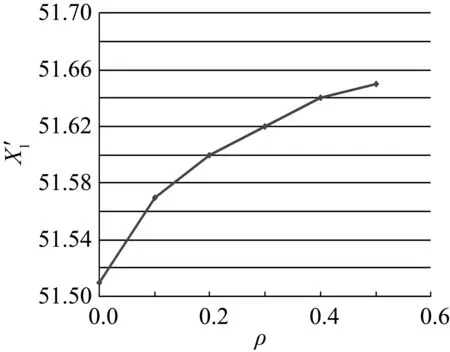
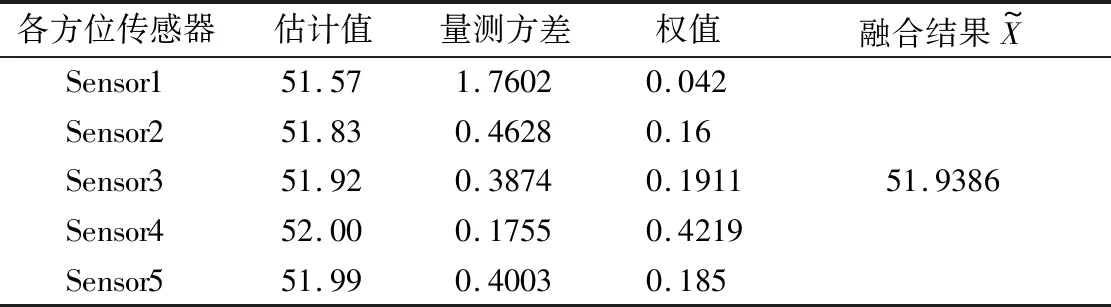
本文利用一致性檢驗方法剔除異常數據,計算均值方差求臨界值及誤差比較均為單層循環,故一致性檢驗方法時間復雜度約為O(k)。通過分批估計融合算法求單傳感器最優監測值的主要計算為分組排序和求均值方差,排序方法采用兩層嵌套循環,時間復雜度為O(k2)。自適應加權融合算法的主要操作為計算n個傳感器的權值,為單層循環,時間復雜度為O(n)。一般地,n< 為了驗證所提改進算法的有效性,通過模擬數據進行仿真分析。表1為以52 ℃為基值的40個監測數據樣本,并設環境噪聲等因素干擾為10%以內,另外設置一定比例的異常值。為了說明方便,不妨設序列為X1={x11,x12,…,x1j,…,x1(40)}。 表1 室內溫度監測數據樣本 5.2.1 數據預處理結果分析 通過對表1數據進行計算,可得均方差: 對于序列X1存在:|ε11|=4.48>3.80768。 所以x11=46.91為可疑值,判定為疏失誤差數據,應予以剔除。剔除完成之后,該組均余下39個數據。經驗證,對于所有X1j(2≤j≤40),均滿足g1j 5.2.2 改進性分批估計結果分析 表2 改進型分批估計融合結果 可分別計算改進前和改進后的監測估計值: 由此可見,改進型分批估計方法估計得到的估計監測值更接近真實值。需要說明的是,分批數可根據傳感器數據監測次數大小而設定,若所獲得監測數據較多時,分批次數越多,方差越小,優點更明顯;若所獲得監測數據較少時,分批次適當減少,可獲得更好的實時性。同時,當數據量較多時,可根據實際設定ρ的取值。針對不同的ρ的取值進行計算分析,如圖3所示。可知,隨著ρ值的遞增,估計值盡管變化微小,但總體趨勢是更接近于真實值的。當ρ達到一定的比例值時,估計值趨于穩定。故依據順序統計理論和實踐經驗,可適當地去除部分最大最小值后分批估計,具有更好的可靠性和準確性,更能夠反映數據的集中情況。 圖3 ρ-估計值變化曲線圖 5.2.3 自適應加權融合結果分析 采用上述方法,監測并統計監測區域內5個不同方位傳感器的數據,進行加權融合,結果如表3所示。 表3 自適應加權數據融合結果 智能家居安全是人類進行生產活動的重要保障。數據監測的準確性和可靠性是實現安全火災監測準確預警的關鍵基礎。數據融合是去除冗余、錯誤和置信度差的數據的有效方法之一。對多源傳感器數據進行預處理及有效的數據融合機制,修正偏差大的數據,刪除不可靠數據,去除冗余,融合高度重復的相關數據,是實現提高數據可靠性、精確性的有效途徑之一。為此,本文提出了一種數據預處理與改進型分批估計加權融合相結合的算法。首先,該算法根據格羅貝斯準則一致性檢驗剔除疏失誤差數據;其次,引入環境因子改進分批估計算法計算當前最優監測值;最后,針對不同方位誤差分布不均勻特點,提出了權值最優分配原則實現自適應加權融合。實驗結果表明,該算法得到的融合結果誤差小,能夠有效提高數據準確性,降低冗余量,穩定性能好。5.2 火災監測實驗數據分析
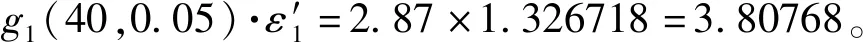

6 結束語

