基于時頻分析的高溫振動環境螺栓連接件松動判別

曹芝腑， 譚志勇， 姜 東， 何頂頂， 費慶國

(1.東南大學 空天機械動力學研究所,南京 211189； 2.東南大學 工程力學系,南京 210096；3.北京臨近空間飛行器系統工程研究所,北京 100076； 4.南京林業大學 機械電子工程學院,南京 210037)

航空航天、能源等諸多領域由于其高溫高壓及強振動的嚴苛工作環境[1]，需要連接結構在此環境下仍能保持足夠的剛度、強度、穩定性及耐久性，傳統材料很難滿足這些要求。因此復合材料由于其比重小、高溫環境下比剛度高、比強度大及服役壽命久等諸多優點，得到越來越多國內外工程研究人員的廣泛重視和研究，并在相關領域得到廣泛使用和發展[2-5]。隨著復合材料在工程中的廣泛應用，復合材料結構設計越來越復雜，加之由于成型工藝水平、設計和使用維護等方面的限制，工程中往往需要將復合材料結構件用連接技術連為整體，復合材料結構的連接問題不可避免。對于復合材料連接結構設計，連接部位是一個相對薄弱的環節，結構的連接破壞是導致結構失效的主要原因之一，尤其是某些重要連接部位的失效破壞，有可能會危及整體結構的安全性和可靠性。

復合材料結構的連接形式主要有3種[6]：膠接連接、機械連接和混合連接。機械連接有螺栓連接、銷釘連接和鉚釘連接等方式，其中螺栓連接具有可靠性高、承載能力強、便于重復拆裝及使用維護簡便等優點[7]，是航空航天領域中復合材料結構的主要機械連接方式。基于復合材料螺栓連接的優點和存在的缺點，有必要對其連接特性進行深入分析，改善不利因素的影響，提高連接效率[8]。

松動失效是最常見的連接結構失效模式，近年來有不少國內外學者致力于連接結構松動誘致失效、故障的研究。研究主要分為兩方面，一方面建立連接結構松動動力學模型，分析連接結構松動對系統動力學特性的影響[9-10]；另一方面是基于結構動響應分析的方法[11-12]，利用動力學實驗中結構非線性動響應，結合非線性動力學理論提取描述結構松動狀態的特征參數，建立結構松動狀態與非線性特征參量之間的關系，進行連接結構松動狀態監測和辨識。

Lü等[13]通過試驗建立螺栓殘余應力與溫度和初始預載荷之間的關系，對復合材料-復合材料，復合材料-金屬和金屬-金屬等不同形式連接結構的松動行為進行分析。該方法能夠利用短期試驗數據構造半解析的時間-溫度相關蠕變率方程，并利用該方程對螺栓連接結構的預緊力松弛現象進行長期預測。趙登峰等[14]建立了螺紋連接松動高度簡化的動力學模型，通過數值仿真和實驗相結合的方法，研究了振動環境中螺栓連接松動過程的動響應特性，提出將諧波失真度作為螺栓連接松動失效的預警指標。Li等[15]針對具有螺栓松動特征的衛星結構，在有限傳感器的條件下，利用二階頻譜對其松動故障進行識別。Nguyen等[16]利用結構健康監測的方法，利用不同螺栓松動工況下的振動響應數據，對風力發電機塔結構進行螺栓松動損傷識別。Amerini等[17]使用健康監測系統研究了螺栓結構在松動和收緊狀態時連接結構接觸面的線性及非線性聲學參數，使用一階聲學矩作為螺栓松緊狀態的指數，這一方法能夠有效評估螺栓連接的健康狀態。另外，研究了單頻和多頻激勵下，高次諧波產生及邊帶調制的非線性方法，其中在單頻激勵下，結構信號的二次諧波幅值與載體信號的基頻振幅的比值可以作為一個可靠的指標，有效評估螺栓的裝配狀態。

本文進行了高溫振動環境下復合材料連接件螺栓松動試驗研究，并使用短時傅里葉變換的時頻分析技術對高溫振動響應進行分析，得到了復合材料連接結構在各試驗條件下的時頻結果。采用二倍頻與基頻振動對應的幅值比作為松動特征值，對復合材料螺栓連接結構在高溫環境下的振動松動狀態進行了綜合評估。

1 松動特征量

圖1所示為螺栓連接件結構，在高溫環境下，結構除產生x方向伸縮變形外，還會產生z向變形。同時由于螺栓的約束和接觸面的粗糙[18]，使得結構連接區域的相互接觸剛度具有非線性特性。一種可行的處理方案是將連接位置的非線性接觸關系簡化為非線性集中力[19]，利用非線性彈簧進行簡化建模，如圖2所示。

考慮如圖2所示的均質等截面簡化梁模型，其在位移為z(t)的基礎振動下的動力學微分方程為

(1)

式中:w為懸臂梁撓度，由線性項wlin和非線性項wnlin組合而成，即w(x,t)=wlin(x,t)+wnlin(x,t)，E為彈性模量，I為梁橫截面慣性矩，ρ為密度，S為橫截面積，δ(x,l)為狄拉克函數，fnl為非線性集中恢復力，z(t)為基礎振動位移。針對均質等截面梁，ρS為常數，則式(1)可簡化為

(2)

式中:FNL表示t時刻的等效非線性載荷，

(3)

其中k1和k2為由于溫度變化引起的螺栓連接界面處的一次和二次剛度系數，是溫度T的函數k1=f(T)，k2=g(T)。

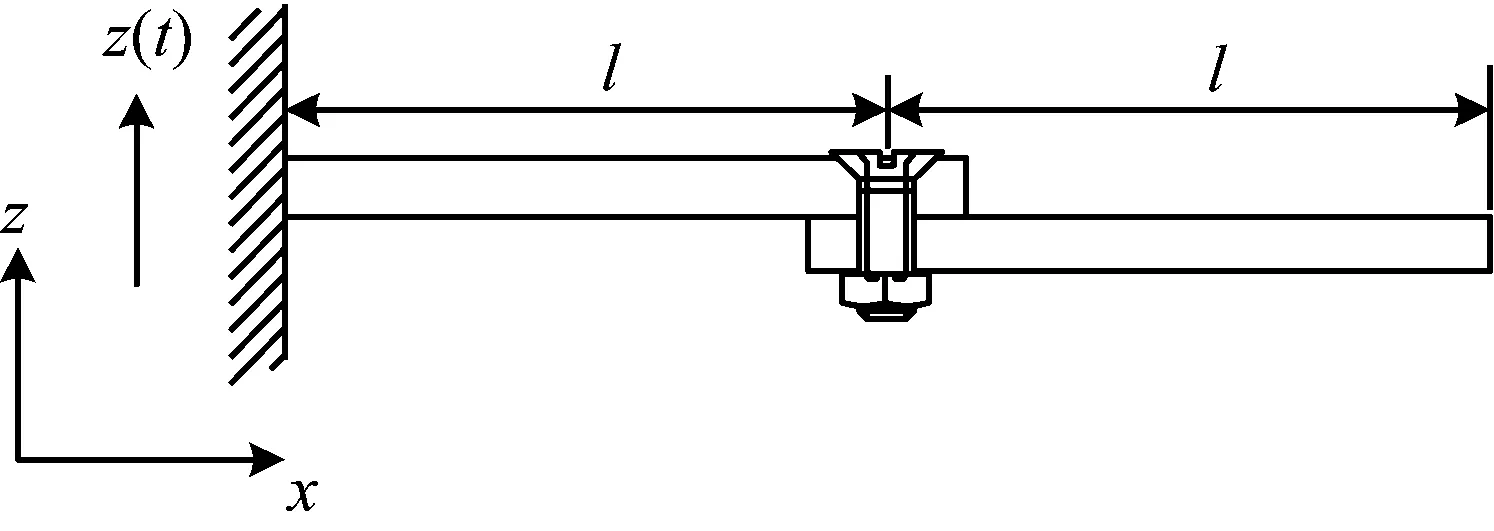
圖1 螺栓連接結構

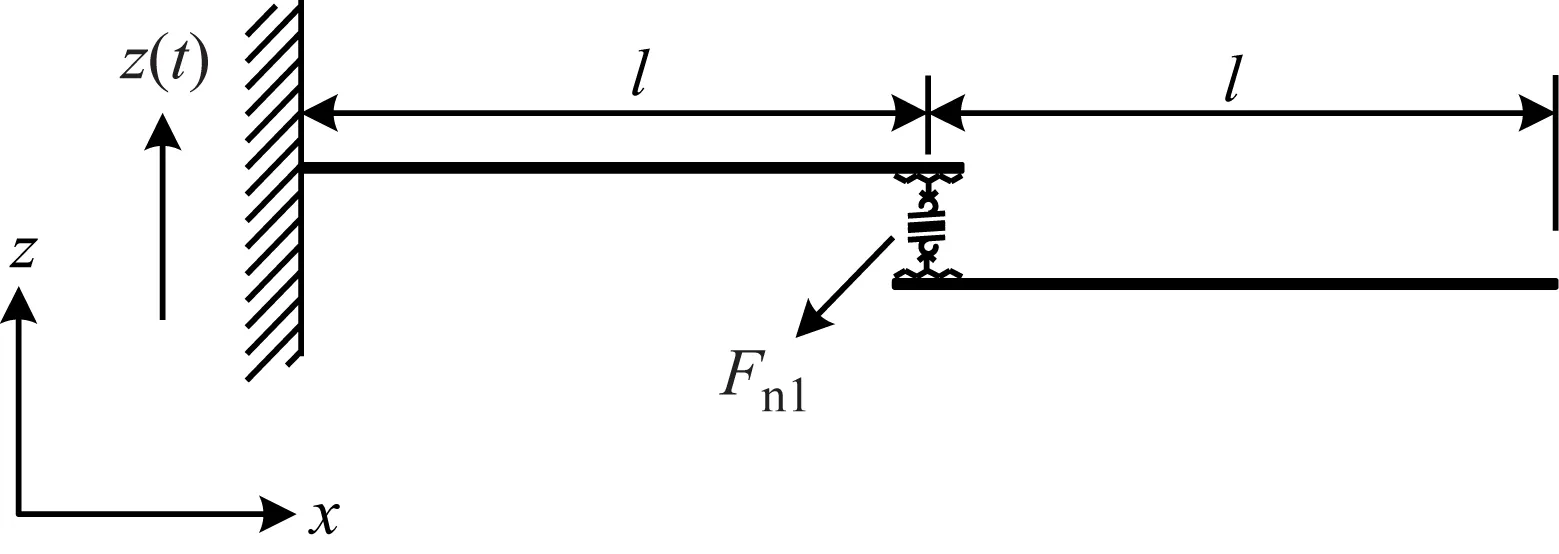
圖2 等效非線性彈簧-梁模型

文獻[20]指出在該等效建模前提下，結構的非線性動響應包含二次諧波項。在頻域下，定義無量綱量r(Z)為二次諧波幅值與基頻幅值的比，作為螺栓連接結構的松動特征指標，對松動特性進行評判

(4)

式中，Z為振動幅值(加速度，速度，位移)。

2 時頻域分析松動判別

時頻域分析方法是非平穩信號處理的一個重要分支，它是利用時間和頻率的聯合函數來表示非平穩信號，并對其進行分析和處理。時頻分析的主要任務是描述信號的頻譜含量隨時間的變化規律。時頻分析的最終目的是建立一種分布，以便在時間和頻率上同時表示信號的能量或強度，得到這種規律后，就可以對連接結構振動信號進行分析和處理，從而提取信號中所包含的特征信息。

傅里葉變換難以反映信號頻率成分的時間特性。但是，如果沿著時間軸把信號在時域上加以分段，每一段作傅里葉變換，計算其頻率，則可以從各段頻譜特性隨時間變化上看出信號的時變特性。這就是目前在時變信號分析中廣泛使用的分析方法：短時傅里葉變換，因其處理過程簡單、高效，得到了廣泛的研究和使用。

短時傅里葉變換[21]的概念最早由Gabor于1946年提出的，其計算公式為

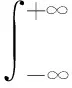
(5)

式中：h*(τ-t)是滑移時窗h(τ-t)的共軛，滑移時窗用來對信號進行分段截取。

3 試驗研究

3.1 試驗件

圖3和圖4分別是復合材料螺栓連接組件的幾何尺寸和實物圖，由同種復合材料板通過復合材料螺栓進行連接，構成復合材料螺栓連接試驗件。

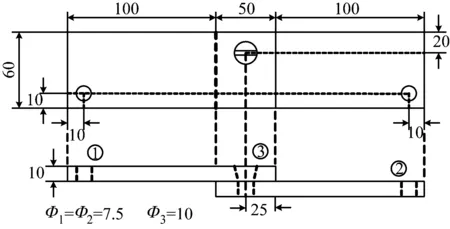
圖3 復合材料螺栓連接組件幾何結構(mm)

圖4 復合材料螺栓搭接板

3.2 試驗系統

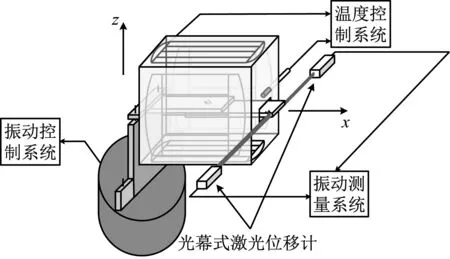
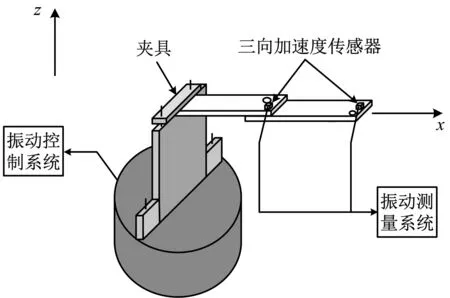
高溫振動試驗系統示意圖和裝置圖如圖 5所示，常溫振動試驗系統示意圖如圖6(a)所示。常溫試驗系統主要包括振動控制系統和接觸式振動測量系統，高溫試驗系統主要包括振動控制系統、溫度控制系統和非接觸式振動測量系統。其中：

振動控制系統主要裝置為電動振動臺(型號：D-600-5；頻率范圍：5～3 000 Hz；額定加速度：100g)；

溫度控制系統由1 000 ℃高溫環境箱(控制精度±1 ℃)及雙鉑銠型(K型)熱電偶(測溫精度±1.5 ℃)組成；

振動測量系統由德國Micro-Epsilon公司的ODC-1200-10光幕式激光位移傳感器及基于Labview的非接觸式激光振動實時測量軟件組成。針對常溫振動試驗，采用接觸式測量方法，如圖6(b)所示。其中傳感器為三向加速度傳感器，型號為LC0122C-50；頻率范圍：1～4 kHz；量程：50g；靈敏度：6.05 pC/g。

(a) 高溫振動試驗系統

(b) 試驗系統布置

夾具如圖6(b)左端所示，該夾具利用4根不銹鋼絲桿配合夾塊緊固，夾塊材料為45號鋼。為保證夾持力均勻一致，對夾緊螺母施加相同大小的擰緊力矩。

3.3 試驗流程

利用上述試驗件及試驗系統分別進行常溫和高溫環境下的振動防松試驗，試驗流程圖如圖3所示。常溫振動防松試驗流程為：常溫環境下，首先對試件進行掃頻試驗和分析，得到分析結果S1；然后進行結構振動試驗(5 min低量級，3 min高量級，15 min低量級)，并在每次振動試驗結束后對構件進行掃頻試驗和分析，得到分析結果S3，S4，S5。

(a) 振動試驗系統

(b) 傳感器布置

與常溫振動防松試驗相比，高溫振動防松試驗在整個流程中會利用溫度控制系統對試件進行加熱，調控試件在振動過程中的環境溫度。針對高溫振動防松試驗，增加高溫和冷卻至常溫后的掃頻試驗步驟，得到分析結果S2和S6。結構振動試驗(5 min低量級，3 min高量級，15 min低量級)及后續的掃頻試驗均在高溫環境下進行，即圖7中虛線框部分。低量級和高量級的載荷譜分別如圖8和圖9所示。掃頻試驗中的掃頻速

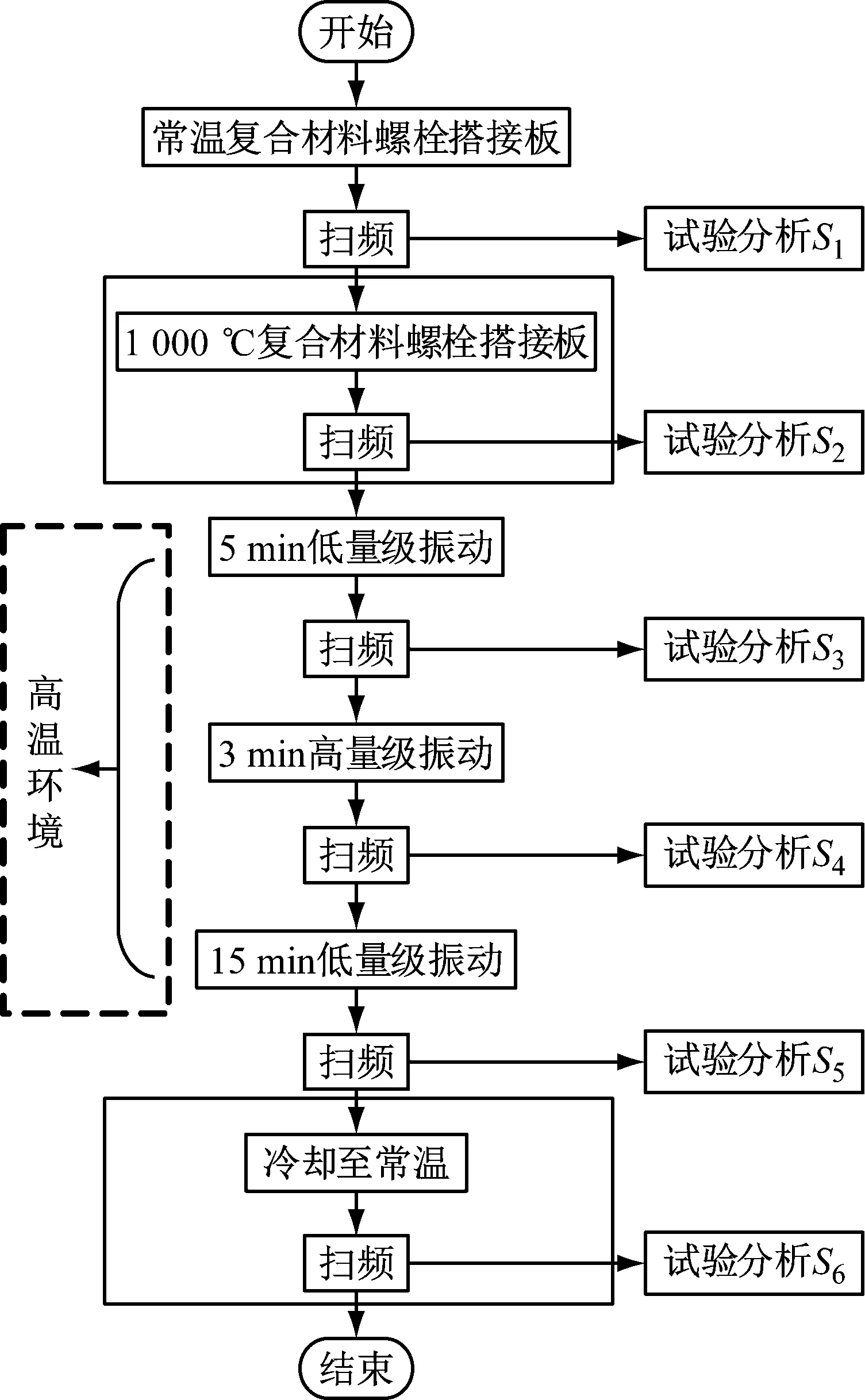
圖7 常/高溫振動試驗流程圖

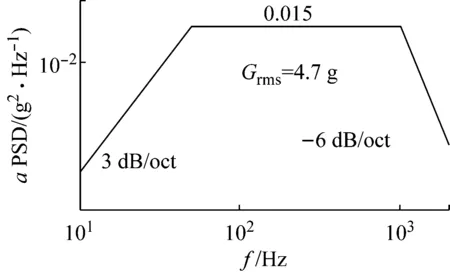
圖8 低量級載荷譜(Grms=4.7g)

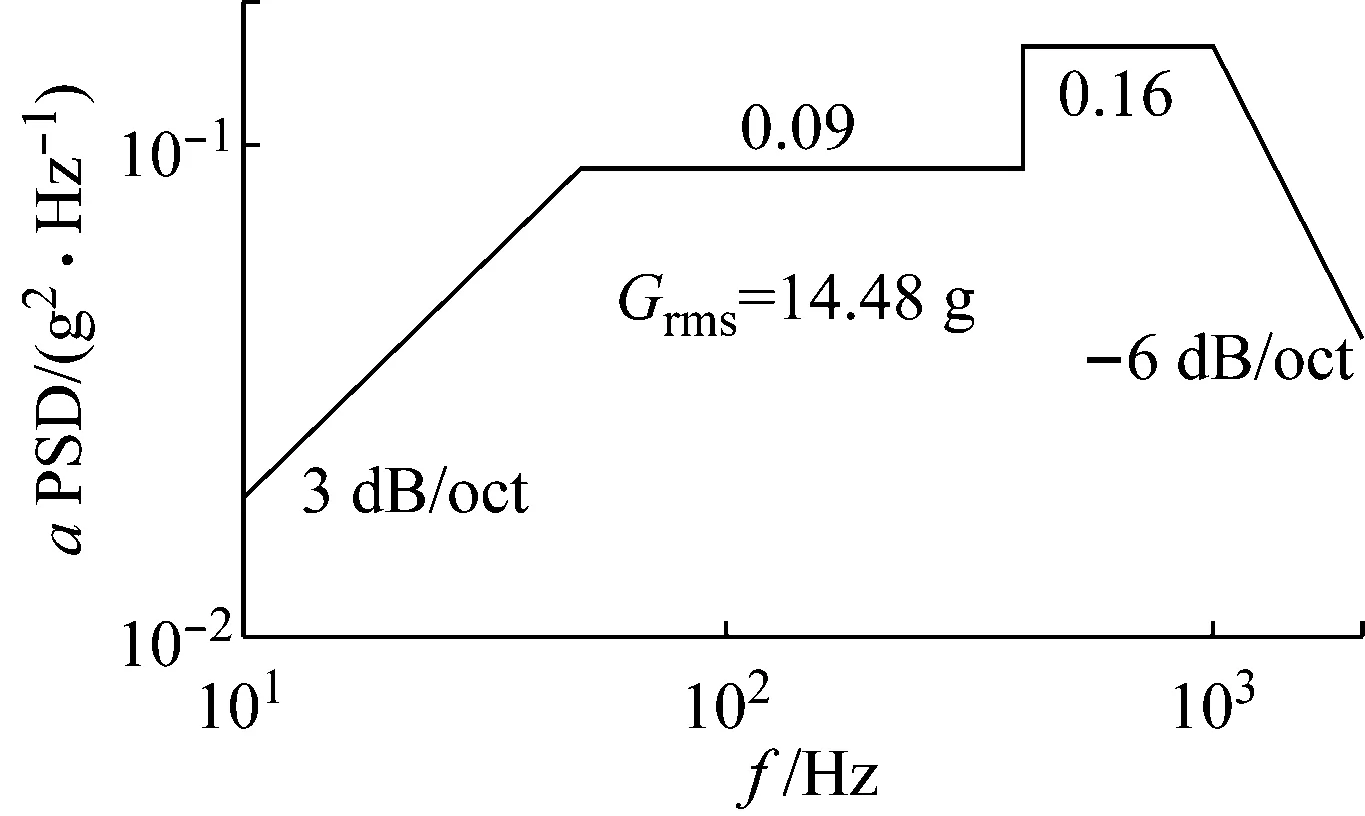
圖9 高量級載荷譜(Grms=14.48g)

度為0.1 OCT/min，掃頻中振動臺加速度值恒定為0.5g。

4 試驗結果與分析

按圖7所示試驗流程完成高溫振動試驗，利用非接觸式振動測量系統獲取響應數據。但由于工頻成分的存在，影響試驗結果的分析。本文利用一維數字濾波方法，濾除工頻和倍頻干擾對試驗的影響

a1y(N)=b1x(N)+b2x(N-1)+…+bnb+1x(N-nb)-

a2y(N-1)-…-ana+1y(N-na)

(6)

式中:x為輸入響應，y為輸出響應，ai和bj分別為濾波系數，na和nb分別為反饋濾波器和前饋濾波器階數。為了實現對工頻干擾信號的濾除，采用二階數字濾波器來消除工頻響應。濾波系數向量a和b分別為[1, -2cosω0, 1]和[1, -2rcosω0,r2]。其中ω0=2πf0/fs，f0為濾波頻率，fs為采樣頻率，r為常數，取0.9。

圖10 濾波前S2時頻分析結果

利用短時傅里葉變換時頻分析技術對試驗結果進行分析，得到高溫振動環境下各試驗流程中的時頻圖，如圖11所示。圖11中Z值最大的點(圖11(a)～圖11(f)中的A點)即為結構振動基頻的振動振幅。然后選取二倍頻所對應的B點，利用式(4)計算得到松動特征指標計算結果:r(Z)=ZB(2ωn)/ZA(ωn)。常高溫環境下，掃頻振動后計算得到的松動特征指標結果如圖12所示。

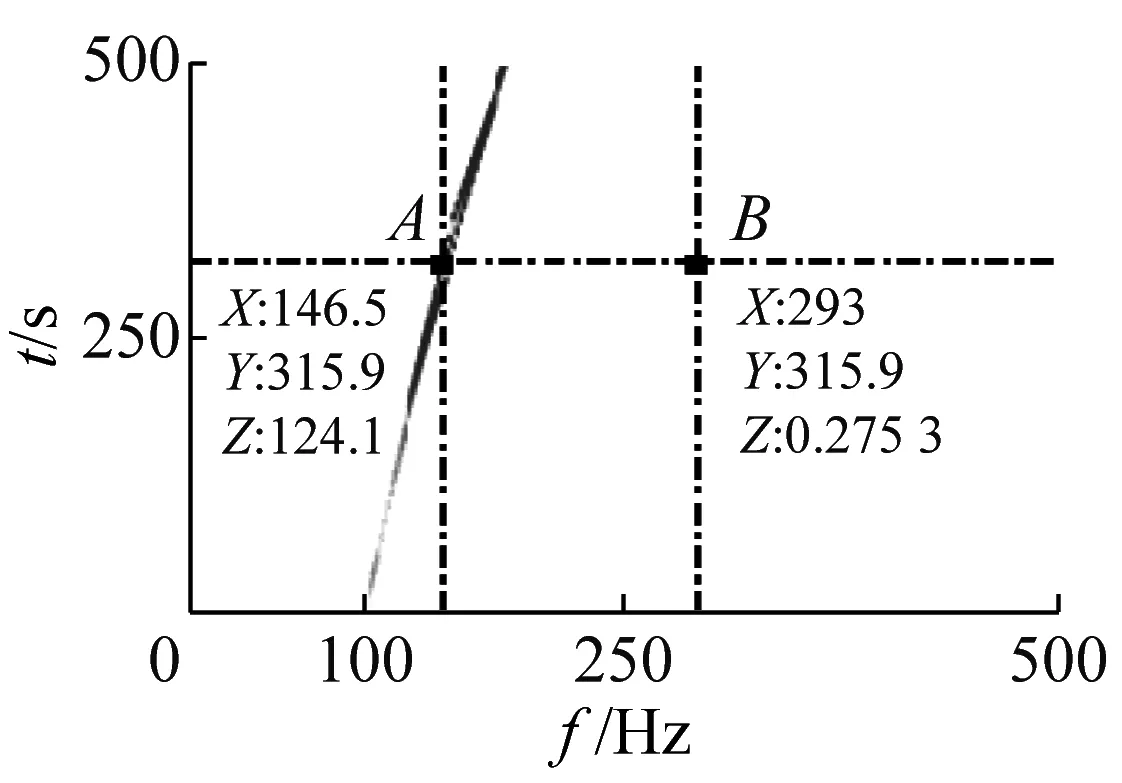
(a) S1

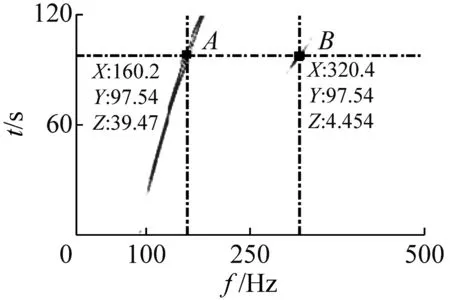
(d) S4

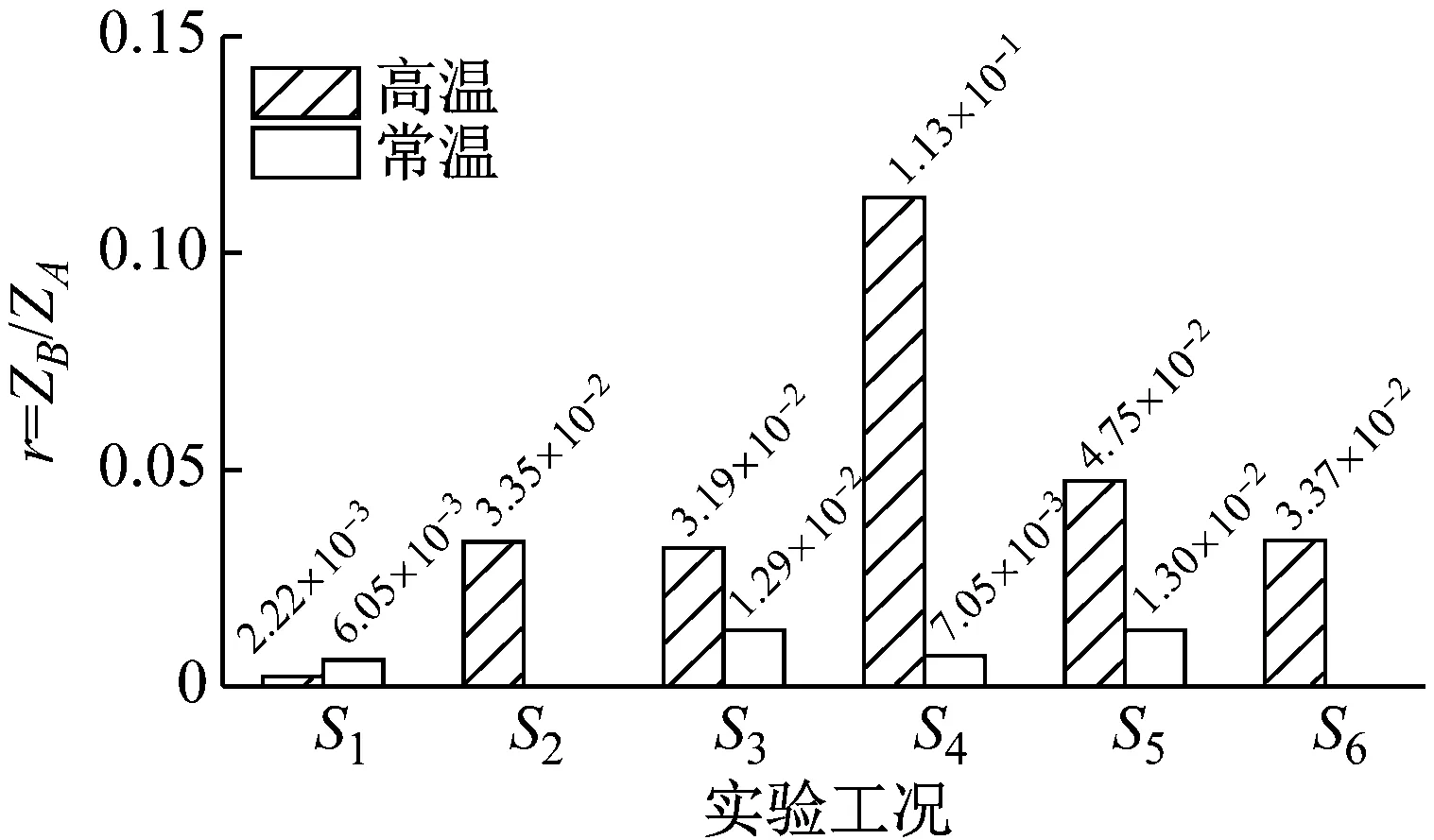
圖12 常溫和高溫下各掃頻試驗后松動指標對比圖

(1) 圖11(a)對應于試驗流程中常溫環境下掃頻振動后的分析結果S1。從圖中可以看出，二倍頻成分不明顯。結合圖 12可知，其初始松動判別指標為6.05×10-3，結構在常溫狀態下未出現連接松動。

(2) 隨著溫度的升高，結構振動基頻增加，且螺栓連接處接觸狀態發生改變，導致圖11(b)呈現多頻成分，松動特征值量級增加，綜合判定連接結構在1 000 ℃高溫環境中開始出現松動跡象。

(3) 圖11(c)～圖11(e)分別為1 000 ℃高溫環境下，5分鐘低量級，3分鐘高量級和15分鐘低量級振動后的掃頻試驗結果。從圖中可以看出，松動特征值在3分鐘高量級振動后達到最大，是常溫狀態下松動特征值的50.9倍。且圖中二倍頻成分均能清晰顯現，說明連接件在高溫振動環境下松動特征明顯。

(4) 圖13所示為試驗前、后螺栓連接局部對比圖，在恢復到室溫后，連接件未見明顯變形。圖11(f)為試驗件恢復到常溫后掃頻試驗分析結果S6，與試驗前比較，二倍頻成分明顯。圖12所示，在高溫環境下，S6對應的松動特征指標為3.37×10-2，為高溫初始狀態的15.18倍。而常溫振動環境下，S5對應的松動指標為1.3×10-2，為常溫初始狀態的2.15倍。比較可知，高溫振動環境下，連接結構更容易產生松動。

(a) 試驗前

5 結 論

本文針對某型復合材料螺栓連接結構進行不同量級下的高溫振動防松試驗，利用時頻分析方法提取振動特征響應，通過定義的高溫松動判別指標r(Z)，實現了高溫振動環境下復合材料螺栓連接結構的松動特性判別及分析。

(1) 時頻分析能夠清晰表明復合材料螺栓連接件在試驗過程中的頻率成分及變化，為特征響應提取提供準確的分析結果。

(2) 結合基頻變化，二倍頻振幅和二倍頻與基頻的振動幅值比值作為松動特性評判的特征量，能夠有效評判復合材料螺栓連接結構在常/高溫環境下的振動松動特性。

(3) 高溫對連接件結構材料屬性的影響，振動對連接處接觸狀態的改變，會導致連接結構在高溫振動后更容易出現連接組件的松動。