基于Tikhonov正則化迭代求解的結構損傷識別方法

夏志鵬， 王樹青， 徐明強， 王皓宇

(中國海洋大學 海洋工程系， 山東 青島 266100)

海洋平臺結構長期服役在惡劣的海洋環境中，容易產生各種形式的損傷，使結構的承載能力下降，甚至導致平臺失效，造成巨大經濟損失及人員傷亡[1]。因此，針對海洋平臺結構的健康監測與損傷識別非常重要。目前結構損傷檢測的方法眾多[2-3]，基于振動測試的結構健康監測技術相對較為簡單且成本較低，是非常具有發展前景的損傷識別技術[4]。其中，基于模態參數的損傷檢測是近年來新興且有效的檢測手段。

在某些情況下，基于模態參數的結構損傷識別過程可以簡化為線性方程組Cα=b的求解問題。當不考慮測量噪聲或噪聲干擾較小時，該系統的求解往往可以得到滿意的結果；而當結構測量模態信息受噪聲影響較為嚴重時，系統的求解結果往往會振蕩發散，導致檢測方法失效。因此，噪聲魯棒性是此類損傷識別技術在發展過程中必須考慮的問題。

從數學的角度看，利用結構的振動測試數據識別其損傷是求解反問題的過程，其不適定性體現在所構建系統的病態上，即微小的測量誤差都可能導致解的振蕩發散。為解決這一問題，學者們做了大量研究[5-11]。其中，基于Tikhonov正則化[12]的方法應用較為廣泛，其基本思想是：用一族與原問題相“鄰近”的適定問題的解去逼近原問題的真實解。王藝霖等將Tikhonov 正則化方法用于結構的損傷識別，一定程度上改善了系統的不適定性，提高了損傷識別精度，并指出正則化方法的作用可通過剛度矩陣條件數的減小來明確衡量。Hua等將Tikhonov正則化與基于靈敏度分析的有限元模型修正方法相結合，進行了簡單框架結構的損傷識別，該方法體現出較好的抗噪性。應用Tikhonov正則化雖然能在一定程度上抑制噪聲，改善損傷識別結果的穩定性，但它的解是過度光滑的，不具有稀疏性[13]。換言之，應用該方法雖然能篩選出真實的損傷信息，但也引入了過多的虛假損傷信息，給損傷識別帶來困難。為改善這一問題，張純等[14]在Tikhonov罰函數項中引入光滑函數，并結合基于靈敏度分析的模型修正方法進行損傷識別研究，明顯改善了損傷識別效果；張純等[15-16]先后將L1和L1/2范數正則化模型修正方法應用于結構損傷識別，有效地改善了基于Tikhonov正則化損傷識別結果過度光滑的缺陷。

利用正則化方法求解線性不適定系統，關鍵在于正則化參數的選擇。上述正則化及其改進方法大都采用L曲線法選取正則化參數，而L曲線的繪制過程往往需要進行大量的試算，對于大型的結構系統，試算過程更加復雜。對于Tikhonov正則化，其參數的合理取值范圍一般較小，系統求解效果對正則化參數的依賴性很高，并且當噪聲水平較高時，L曲線趨于平直，很難通過該方法選取合適的正則化參數[17]。

解的過度光滑及正則化參數選擇時試算量過大是制約Tikhonov正則化應用于損傷檢測的兩大難題。對此，本文綜合上述正則化方法的優勢及缺陷，提出了一種基于Tikhonov正則化的迭代求解方法，用于測量噪聲影響下損傷識別線性系統的求解。該方法基于Tikhonov正則化理論，能夠在迭代過程中利用二分法自適應調整正則化參數，并通過迭代的方式重構正則化權重矩陣，能夠充分抑制噪聲，保留實際損傷信息。通過一個數值算例，驗證了本文方法的有效性。

1 基本理論

1.1 交叉模態應變能方法

交叉模態應變能(CMSE)方法[18-21]是一種典型的以線性系統求解結構損傷信息的識別方法。該方法計算簡單，并且可以同時識別結構的損傷位置和損傷程度。與其他的檢測方法相比，該方法有如下優點：不需要質量歸一化的振型；僅利用結構損傷前后的較少幾階模態即可判斷結構的健康狀況。因而，應用CMSE方法進行損傷檢測具有很好的發展前景。

設K和M分別為結構剛度和質量矩陣，λi和Φi分別表示第i階特征值和特征向量。結構損傷前后的特征方程可表示為

KΦi=λiMΦi

(1)

(2)

本文中，上標“*”用來表示損傷后的情況。

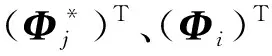
(3)

(4)

對式(3)兩邊取轉置，并考慮矩陣K和M的對稱性得

(5)

聯立式(4)、(5)，并考慮到M*=M，可以得到：

(6)

本文中，單元損傷通過桿件模量的等效折減進行模擬，即對第n個結構單元，其損傷后的模量值

(7)

式中，En為損傷前第n個單元的模量，αn為相應的損傷程度。則損傷后結構的剛度矩陣可寫為

(8)

式中：Ne為結構單元的總數；Kn為第n個單元損傷前的單元剛度矩陣。

將式(8)代入式(6)并整理后得

(9)

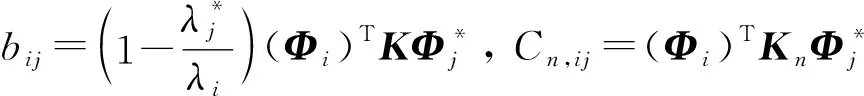
用Ni和Nj分別表示結構損傷前后的模態階數，可以構建Nq=Ni×Nj個線性方程，將其寫成矩陣形式

Cα=b

(10)

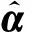
(11)

可采用奇異值分解法(SVD)尋求最小二乘解。對系數矩陣C作奇異值分解

(12)

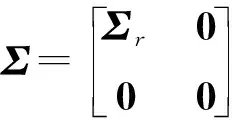
(13)

當測量模態空間不完備時，采用Guyan擴階法[22]對不完備振型進行如下擴階處理

(14)

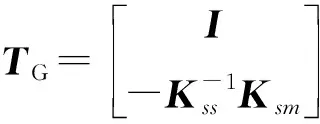
1.2 Tikhonov正則化方法

Tikhonov方法的思想是將最小二乘解和最小范數解綜合考慮。對于式(9)所示的線性系統，可建立目標函數如下

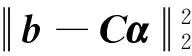
(15)

其中L為Ne階正則化矩陣，一般作變換將L轉化為單位矩陣I[23]。ξ為正則化參數，用于控制最小二乘解和最小范數解之間的平衡。

當L為單位矩陣時，式(14)等價于求解

(CTC+ξ2I)α=CTb

(16)

該方程的解為

(17)

對系數矩陣C作式(11)所示的奇異值分解，則式(17)可表示為

(18)

其中

(19)

稱為Tikhonov過濾因子，顯然，f(σi)的大小依賴于奇異值σi和正則化參數ξ。而當ξ?σi時，式(18)轉化式(13)所示的最小二乘解。

2 基于Tikhonov正則化的迭代求解方法

Tikhonov方法的正則化矩陣一般為單位矩陣，這表明Tikhonov正則化方法對各單元損傷參數進行了相同的加權平滑處理，其解不具有稀疏性。而對于損傷結構而言，其損傷參數是稀疏分布的，即除個別損傷單元外，解向量的大部分元素均為零。因此，傳統的Tikhonov正則化應用于損傷檢測時存在一定的缺陷。適合損傷識別的理想正則化方法應具有如下特性：對于真實的損傷信息，正則化的平滑作用較小以便保留結構的實際損傷信息，即正則化矩陣中對應的權重較小；當出現虛假損傷時，增強平滑作用以消除噪聲導致的虛假損傷信息，即正則化矩陣中對應的權重較大。為了達到這一效果，本文考慮通過具有稀疏性的損傷參數來重新構造正則化矩陣，構造形式如下

L(α)=diag{(|α1|+ε)-1,…,(|αn|+ε)-1}

(20)

其中αi為第i個單元對應的損傷參數，ε為一正常數，避免因αi→0而導致矩陣對角元素趨于∞。

當L為一般的對角矩陣時，式(15)等價于求解

(CTC+ξ2LTL)α=CTb

(21)

該方程的解為

(22)

由于正則化矩陣L(α)需用損傷參數α來構造，而α為待求的未知量，因此，需要采用迭代的方式進行求解。

需要注意的是，正則化參數ξ的選取是利用正則化方法求解線性不適定問題的關鍵。前述研究中，學者們一般采用L曲線法選取正則化參數，而L曲線的繪制通常需要進行大量的試算，尤其是對于復雜的大型結構系統。此外，當噪聲水平較高時，L曲線趨于平直，很難通過該方法選取合適的正則化參數。為解決正則化參數選取時需要大量試算的問題，提出了一種奇異值二分法用于本文新方法中正則化參數的選取。

基于Tikhonov正則化迭代求解(Tikhonov Regularization Iterative Method，TRIM)的損傷識別過程如下：

步驟1構建損傷檢測線性系統，求得系統的初始解

根據結構損傷前后的模態信息利用損傷檢測方法(如CMSE)構建方程組Cα=b。對系數矩陣C進行奇異值分解，獲得系統的r個奇異值σ1≥σ2≥…≥σr≥0。

(23)

步驟2調整正則化參數，重構正則化矩陣，進行第k次迭代求解

(1) 基于奇異值二分法調整正則化參數ξ

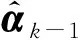
(24)

相應的正則化參數調整為

(25)

上述選擇和調整正則化參數的方法，我們稱之為奇異值二分法。

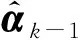
(26)

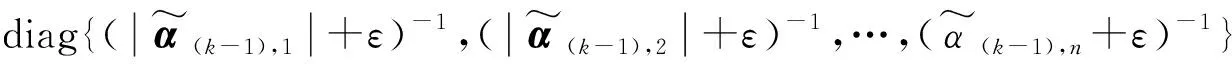
(27)

此處ε統一取為0.01%，以減小對損傷檢測結果的影響。

(3) 進行第k次求解

應用新的迭代參數ξk和矩陣Lk，計算新的解向量

(28)

步驟3重復步驟2所述過程，直到前后兩次迭代求解的向量差值滿足如下條件

(29)

其中δ為收斂閾值，本文建議δ=0.1%，在保證求解精度的同時，控制所需要的迭代步數。基于新方法的最終損傷識別結果為

(30)

基于Tikhonov正則化迭代求解的CMSE損傷檢測(簡稱CMSE-TRIM)流程如圖1所示。

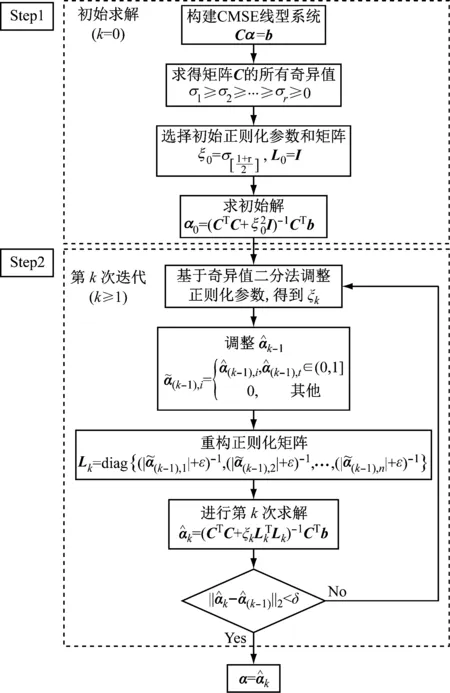
圖1 CMSE-TRIM損傷檢測流程圖

3 數值算例

3.1 海洋平臺結構

本算例的研究對象為一個近海導管架平臺結構[24]，如圖2所示。該結構由36個外徑為17.8 cm，壁厚為0.89 cm的均勻鋼管構件組成，每根鋼管劃分為一個單元。結構三層標高分別為9.14 m，18.29 m和27.43 m。底部和頂部的邊長分別為10.97 m×10.97 m和3.66 m×3.66 m。平臺的四條腿固定于地面。選用材料為鋼材，彈性模量2.1×1011Pa，密度7 850 kg/m3，截面面積2.825×10-3m2，截面慣性矩2.89×10-6m4。按照有限元方法組建整體質量矩陣(采用集中質量法)和整體剛度矩陣，進行特征值分析，得到有限元模型的前三階頻率分別為7.51 Hz、8.80 Hz和8.88 Hz。平臺前三階振型如圖3所示。

圖2 海洋平臺結構示意圖

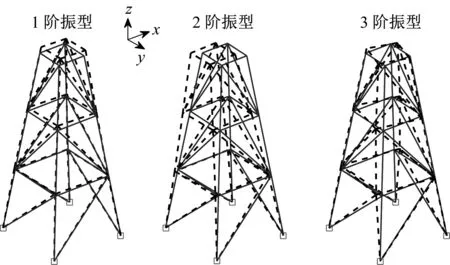
圖3 有限元模型前三階振型

3.2 損傷工況設置

由于實際測試中結構的高階模態一般難以激勵，轉動自由度信息難以測量，因此本文算例中假設僅能測得損傷結構1～3階頻率以及振型中的平動自由度信息，并且所測振型信息含有一定水平的噪聲。

為了研究本文提出的方法在不同因素影響下的損傷識別效果，算例中設置了四類影響因素：① 損傷位置敏感性；② 損傷程度敏感性；③ 噪聲水平敏感性；④ 模態階數敏感性。分別探討不同影響因素下的損傷識別效果。結構損傷后的振型信息添加一定水平噪聲，噪聲添加方式如下

φi,j=φi,j(1+μGi,j)

(31)

式中,μ為噪聲水平；Gi,j為均值為0、方差為1的高斯隨機數；φi,j為對應于第i個自由度的第j階振型值。實測頻率信息一般較為準確，因此算例中不考慮噪聲對頻率的影響。

4 損傷識別與結果分析

本文采用Guyan擴階方法對仿真模擬得到的損傷后模態振型進行擴階處理，利用損傷前后的模態信息構建CMSE方程，求解36個單元(n=36)的損傷參數。并對比CMSE-Tikhonov(基于Tikhonov正則化求解的CMSE損傷檢測)和CMSE-TRIM的損傷識別效果。

4.1 損傷位置敏感性

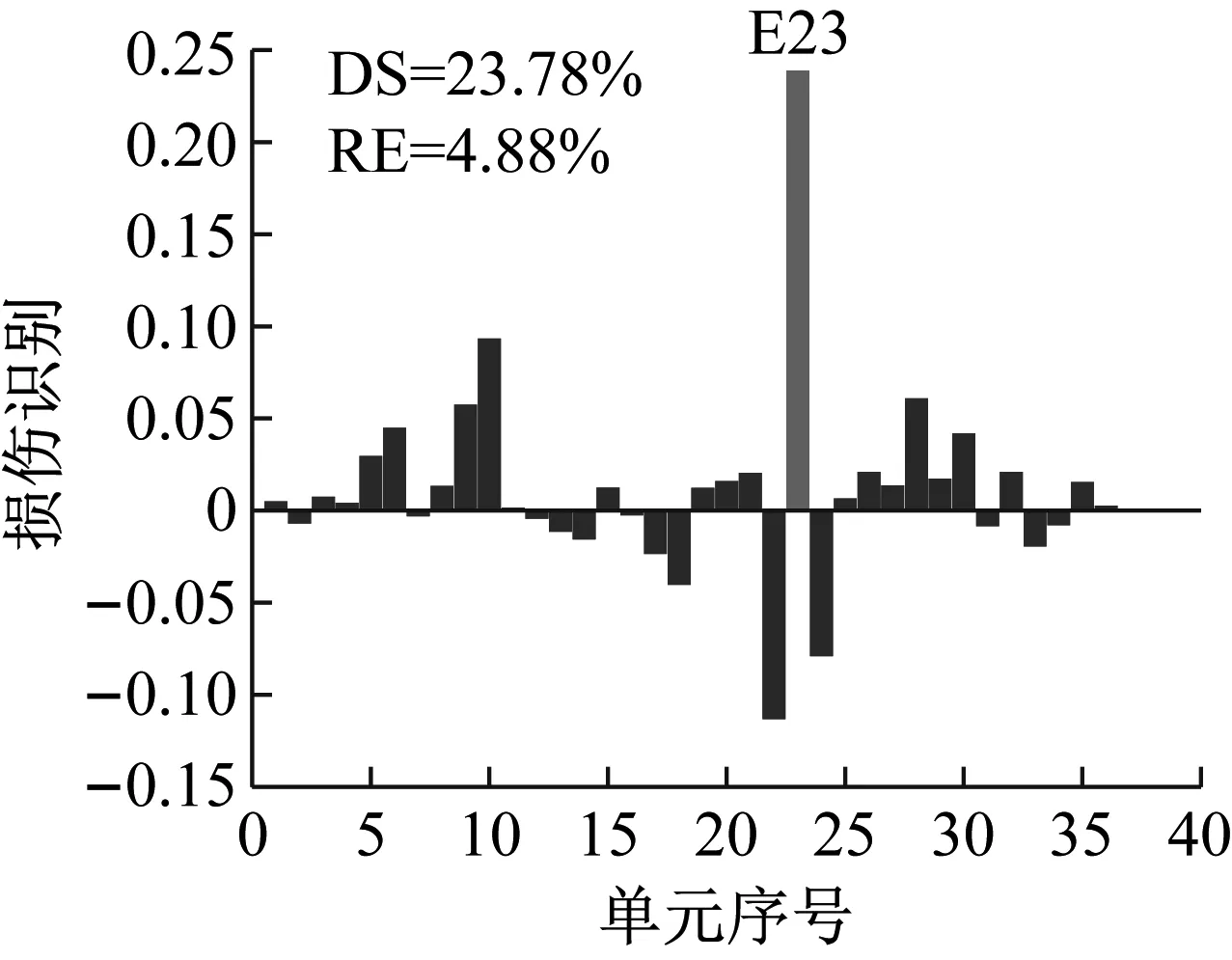
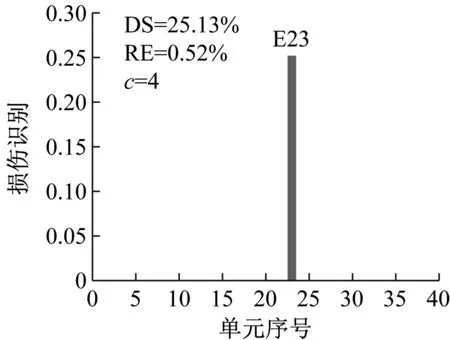
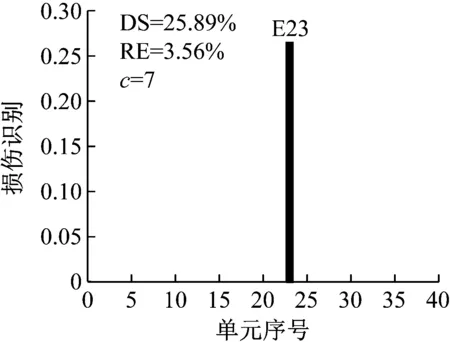
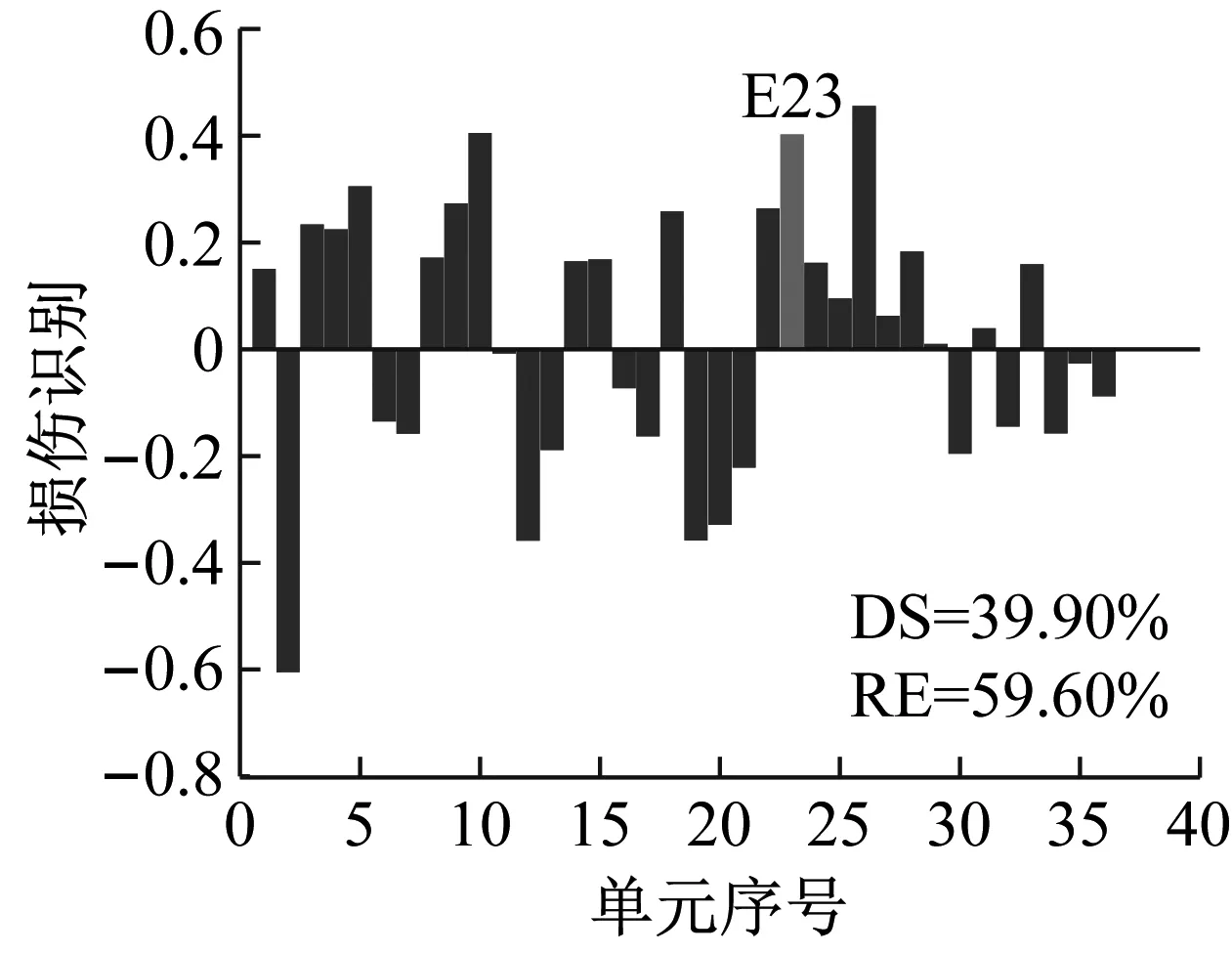
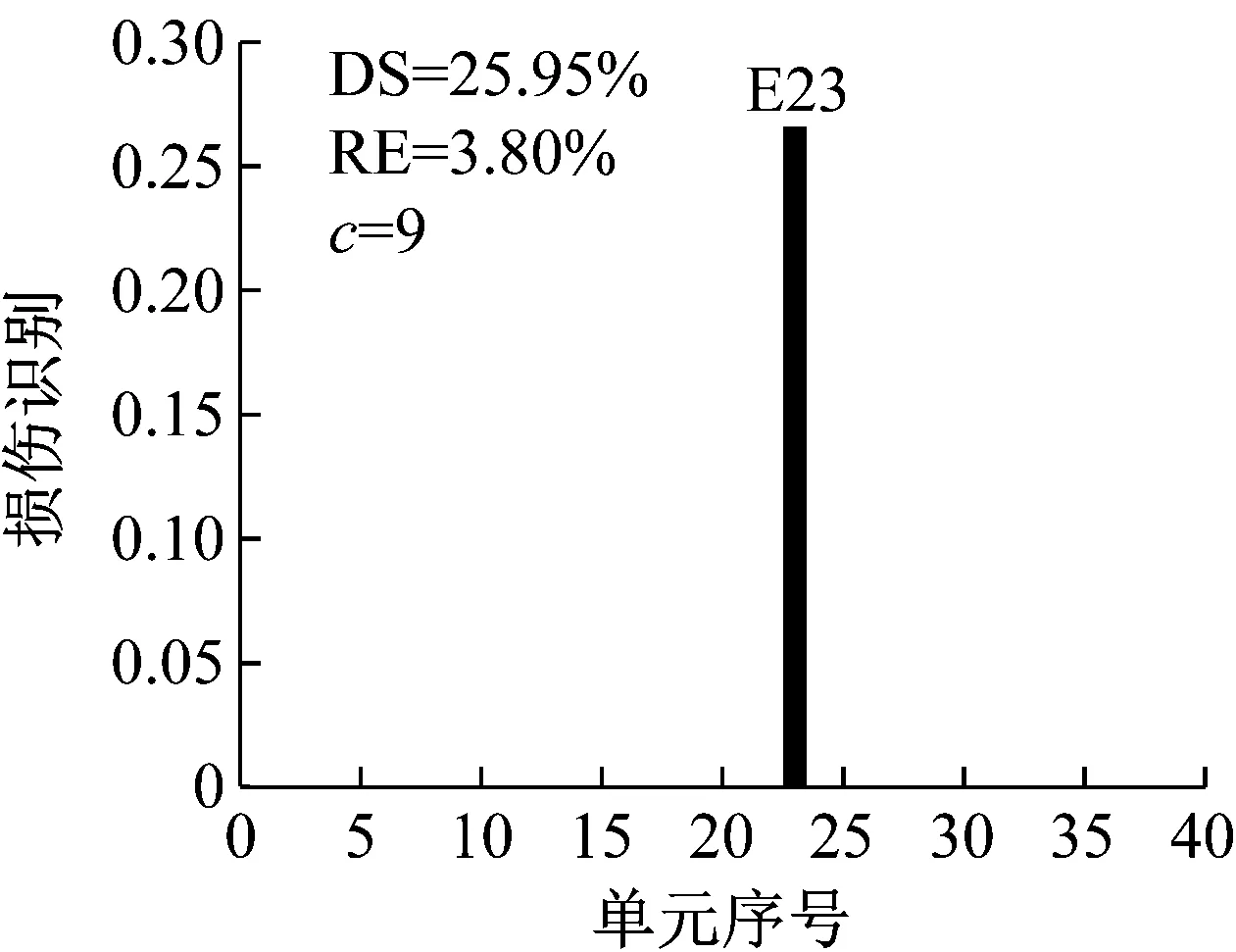
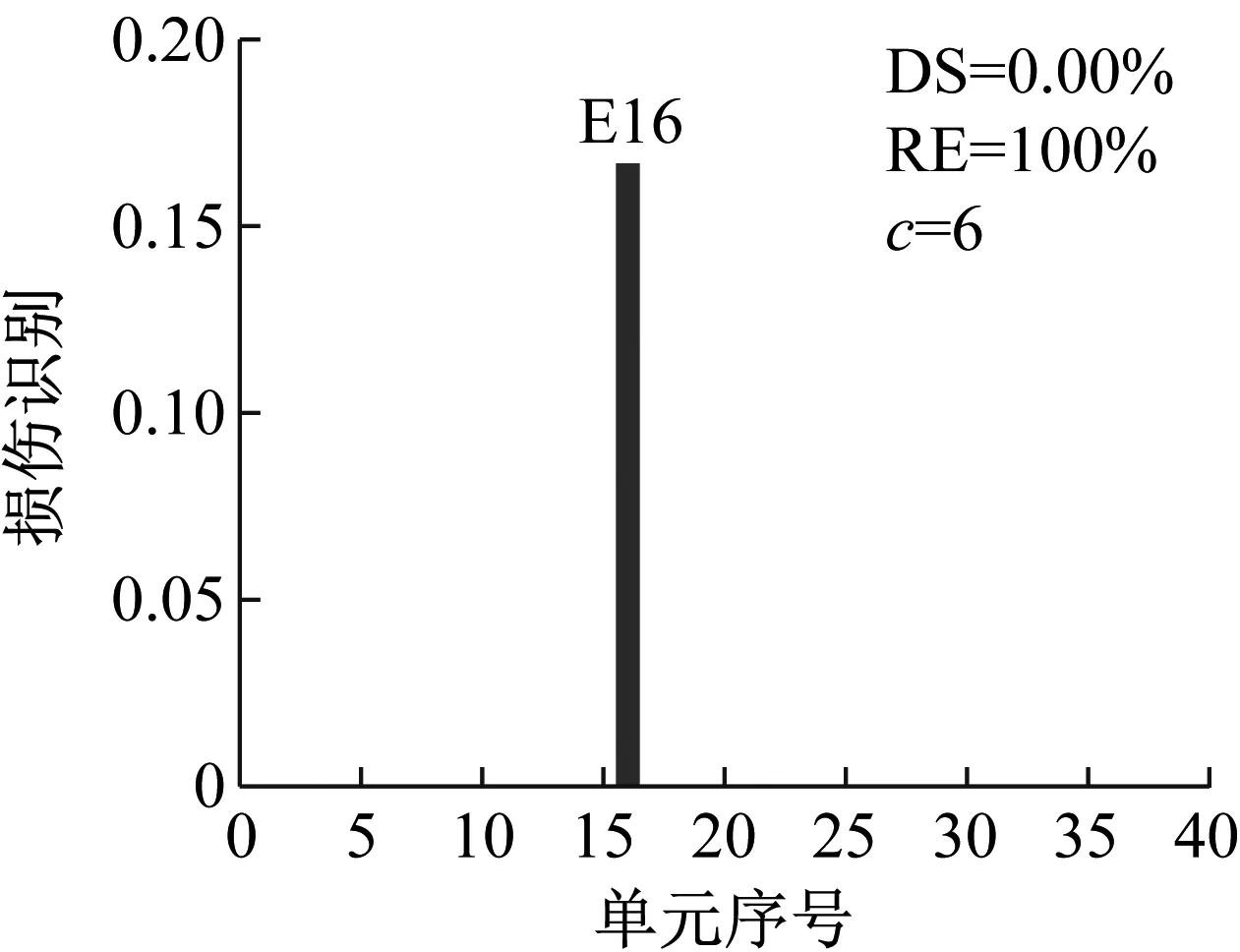
設置噪聲水平1%，損傷程度25%，選用結構損傷后1～3階模態，研究損傷方法對不同類型損傷構件(工況S1：13，工況S2：20，工況S3：23)的損傷識別效果。

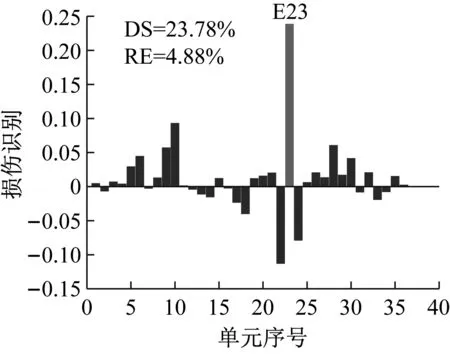
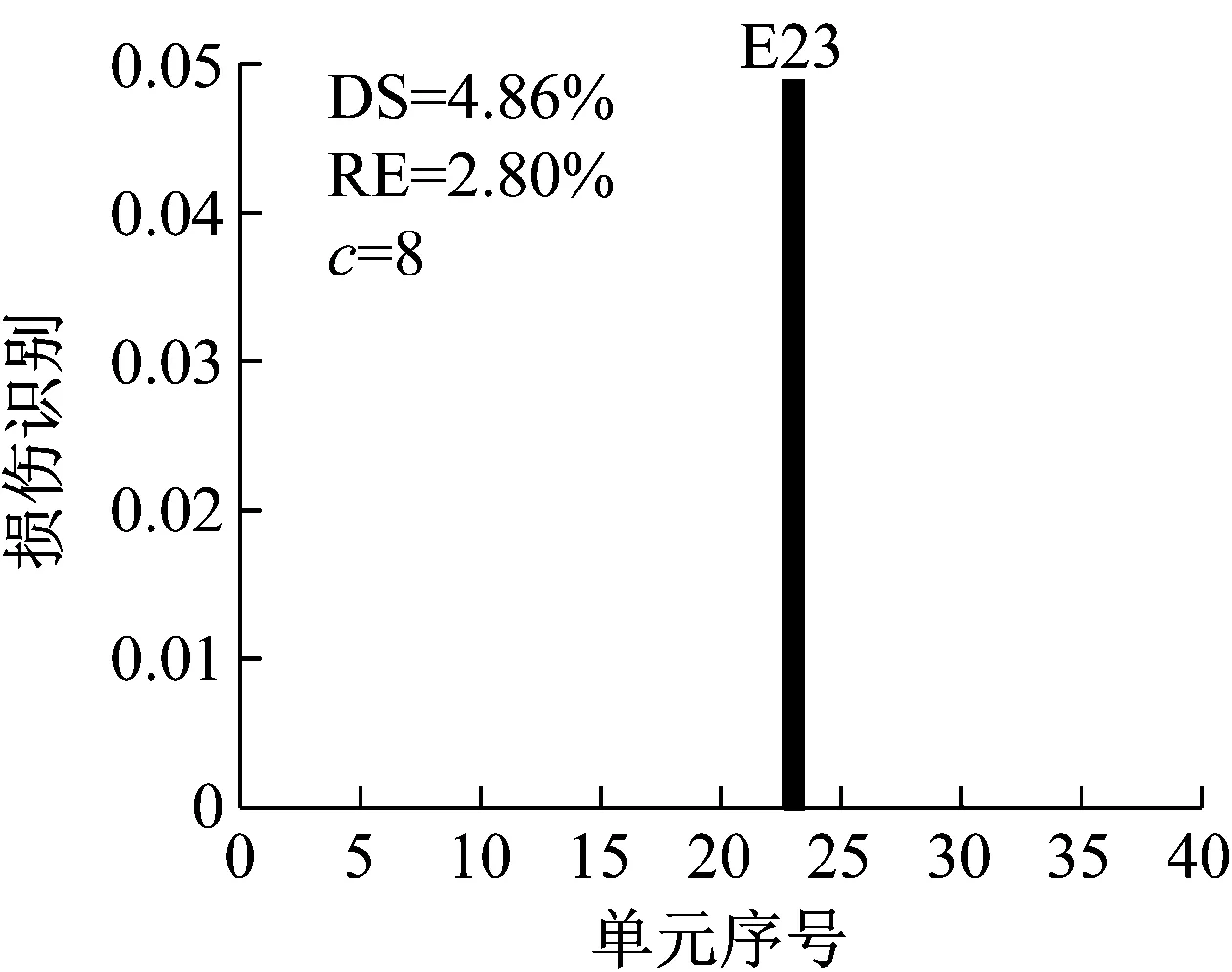
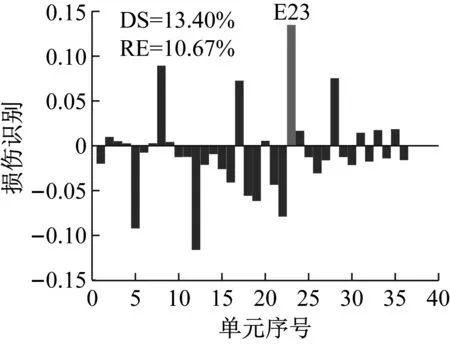
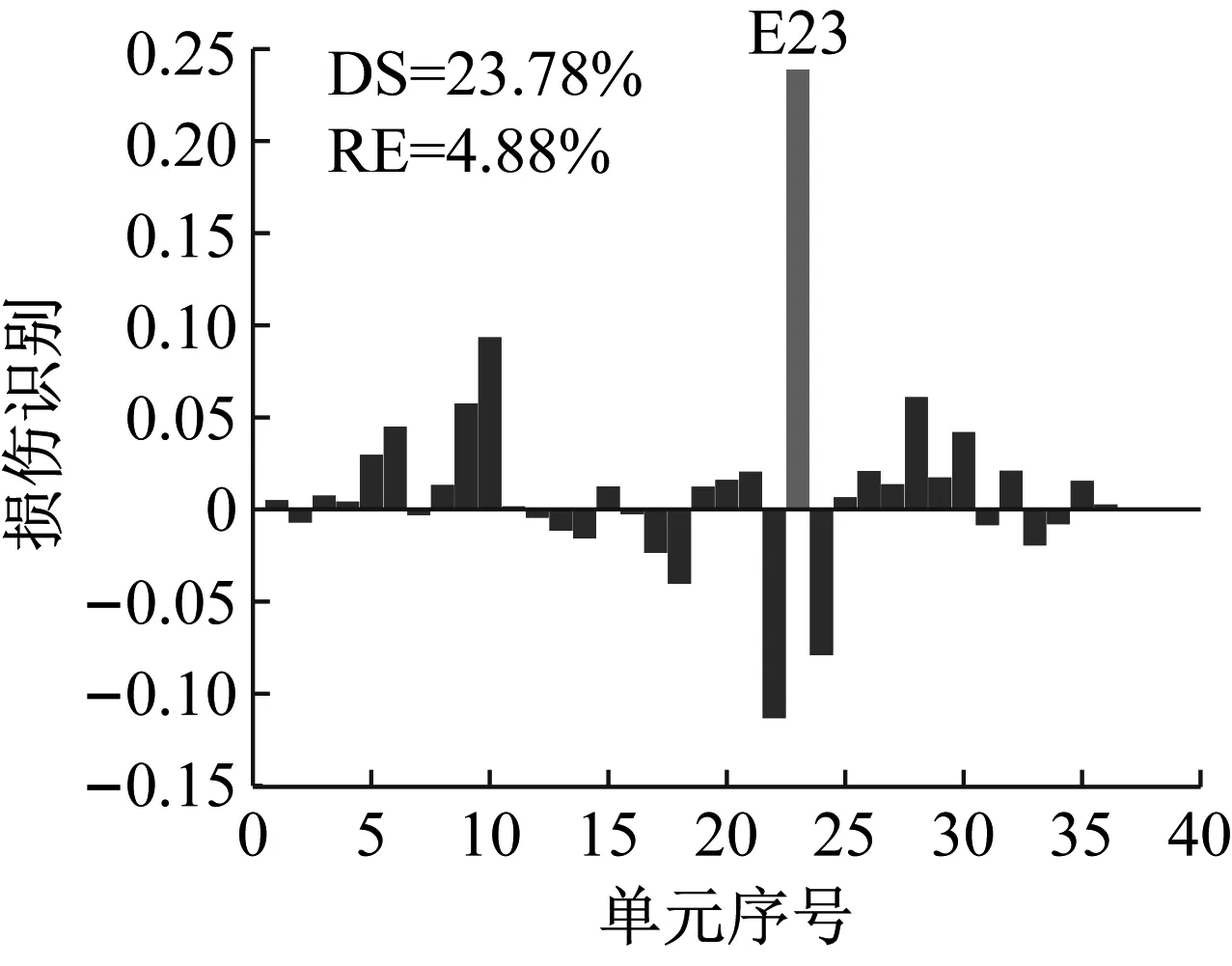
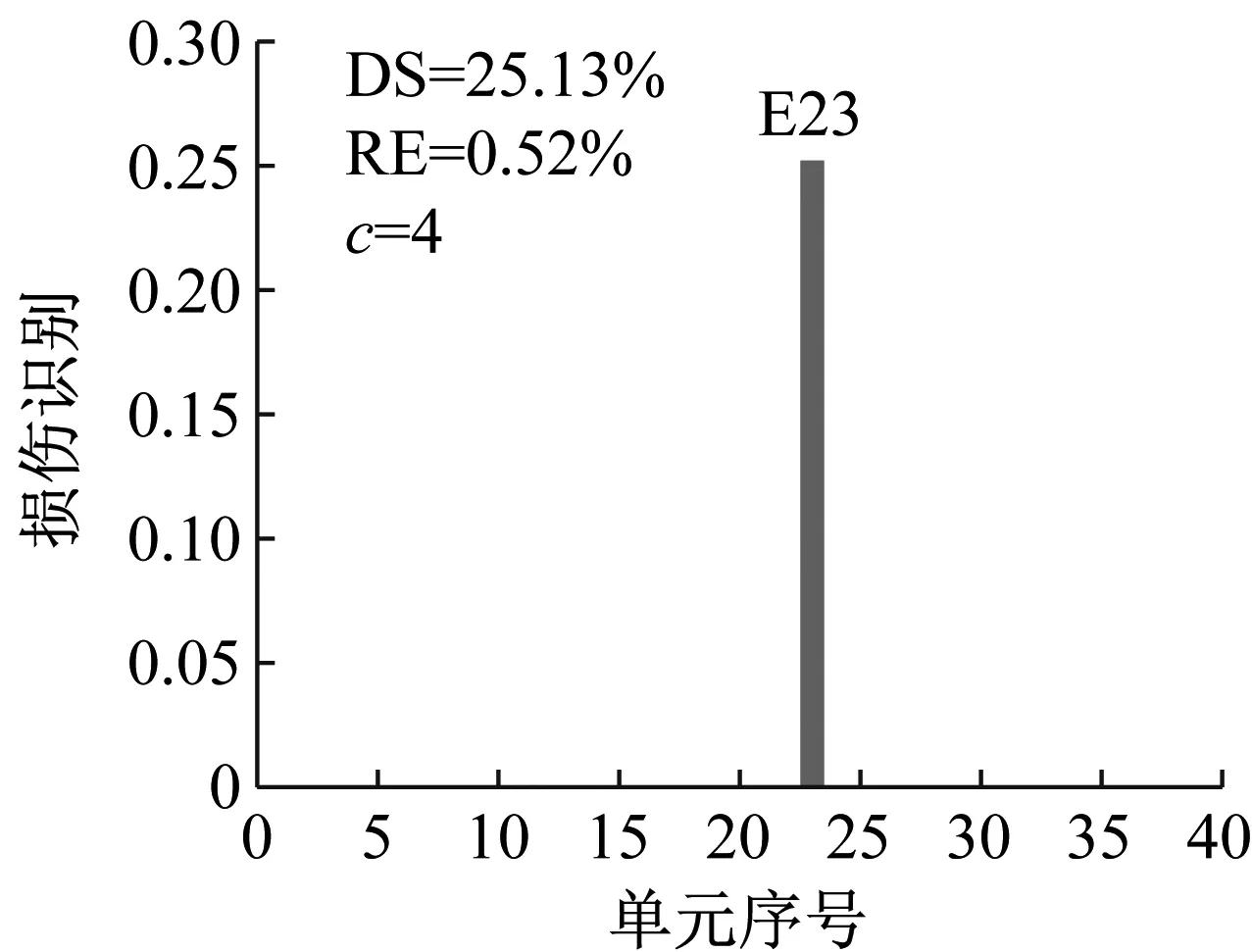
工況S1設置13號單元發生25%損傷，在測量模態空間不完備及1%噪聲影響下利用CMSE-Tikhonov方法進行損傷識別，具體求解過程如下：首先根據1.1節內容構建CMSE方程組Cα=b，對系數矩陣C進行奇異值分解，并將得到的所有奇異值分別假設為正則化參數，根據式(16)進行試算并繪制L曲線圖(如圖4)；找出L曲線最大曲率點所對應的奇異值，作為最終選用的正則化參數，進而求解損傷向量。由L曲線法選取的正則化參數為ξ=7.20×107，根據式(16)進行求解，最終識別結果如圖5(a)所示，其中，深灰色表示干擾項，淺灰色表示損傷單元的損傷指標。此外，圖中DS(damage severity)，表示實際損傷單元的損傷程度；RE(relative error)，表示評估的損傷程度與真實值的相對誤差；c表示迭代的總次數。

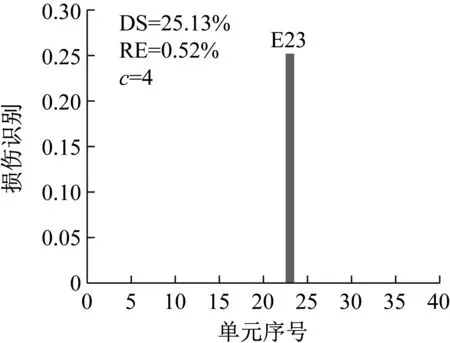
應用CMSE-TRIM對工況A進行損傷識別的過程如下：構建CMSE方程組Cα=b，對矩陣C進行奇異值分解，并直接選取矩陣C的中間奇異值σ18=1.06×108作為初始的正則化參數；按照圖1所示流程進行迭代求解，迭代9次后計算結果達到收斂閾值，最終求解結果如圖5(b)所示(圖中c表示迭代次數)。工況B和工況C損傷識別過程與工況A類似，具體流程不再贅述，最終求解結果分別見圖6和圖7。應用TRIM方法所得損傷單元各迭代步下的計算結果如圖8所示。

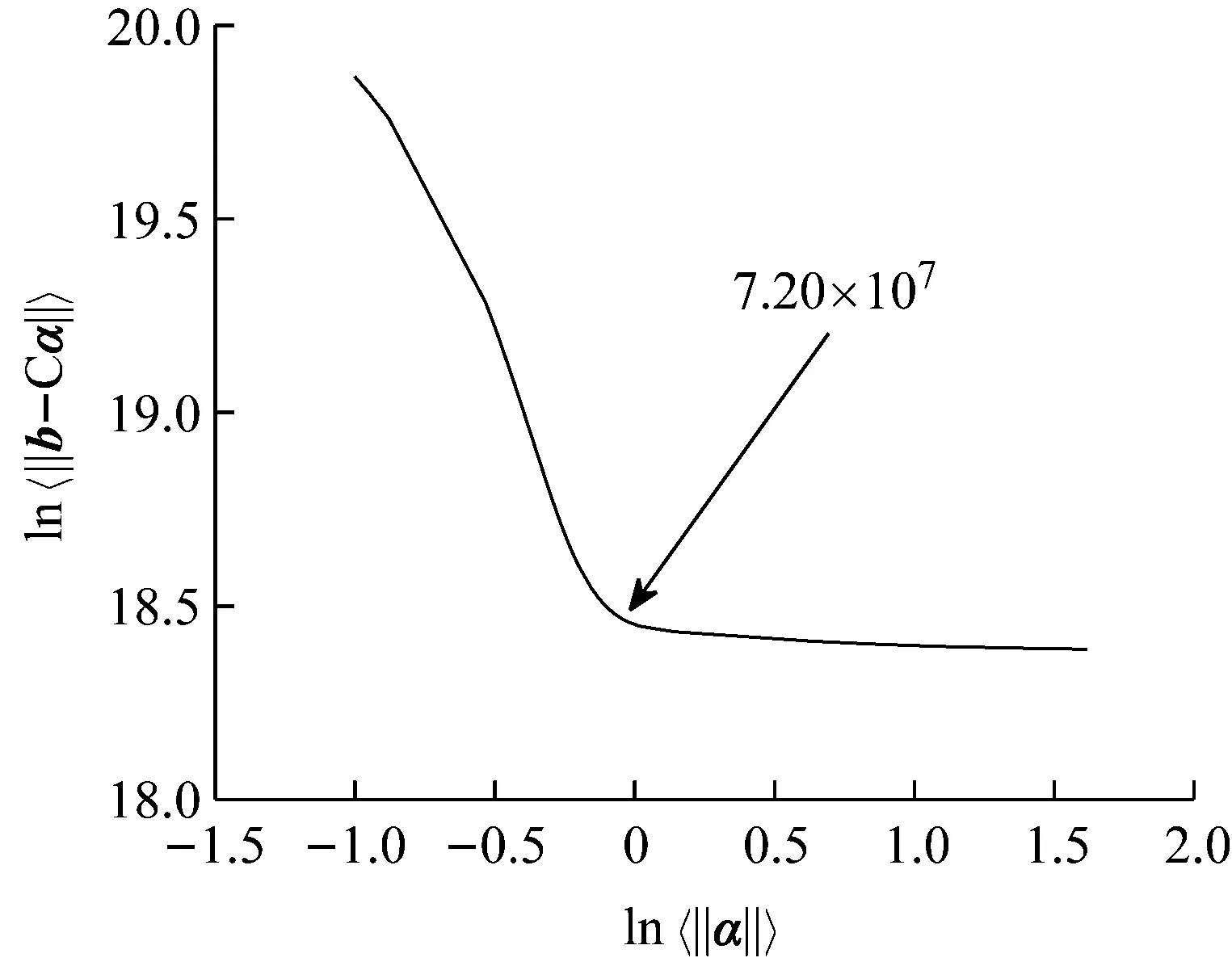
圖4 工況S1 “L曲線”圖

對比三種不同損傷位置下CMSE-Tikhonov求解結果，可以看出，該方法對立柱單元損傷檢測效果最好，斜撐次之，橫撐檢測效果最差。相比之下，CMSE-TRIM方法對上述三工況的損傷識別結果都非常好，無論是在損傷定位還是損傷程度識別方面都明顯優于CMSE-Tikhonov方法。從圖8中損傷單元各迭代步計算結果可以看出，13號橫撐損傷時迭代次數最多(9次)，20號斜撐次之(5次)，識別23號立柱損傷所需迭代次數最少(4次)。迭代次數的多少側面反映出不同類型損傷單元的損傷識別難易程度，即相同條件下，立柱損傷最容易識別，斜撐次之，橫撐損傷最不易識別。此外，從圖8中13號單元迭代結果變化可以看出，該計算結果經歷了由大變小，由小變大，最后逐漸趨于穩定這幾個階段，體現出TRIM方法能夠自適應調節計算結果的特性。

(a) CMSE-Tikhonov

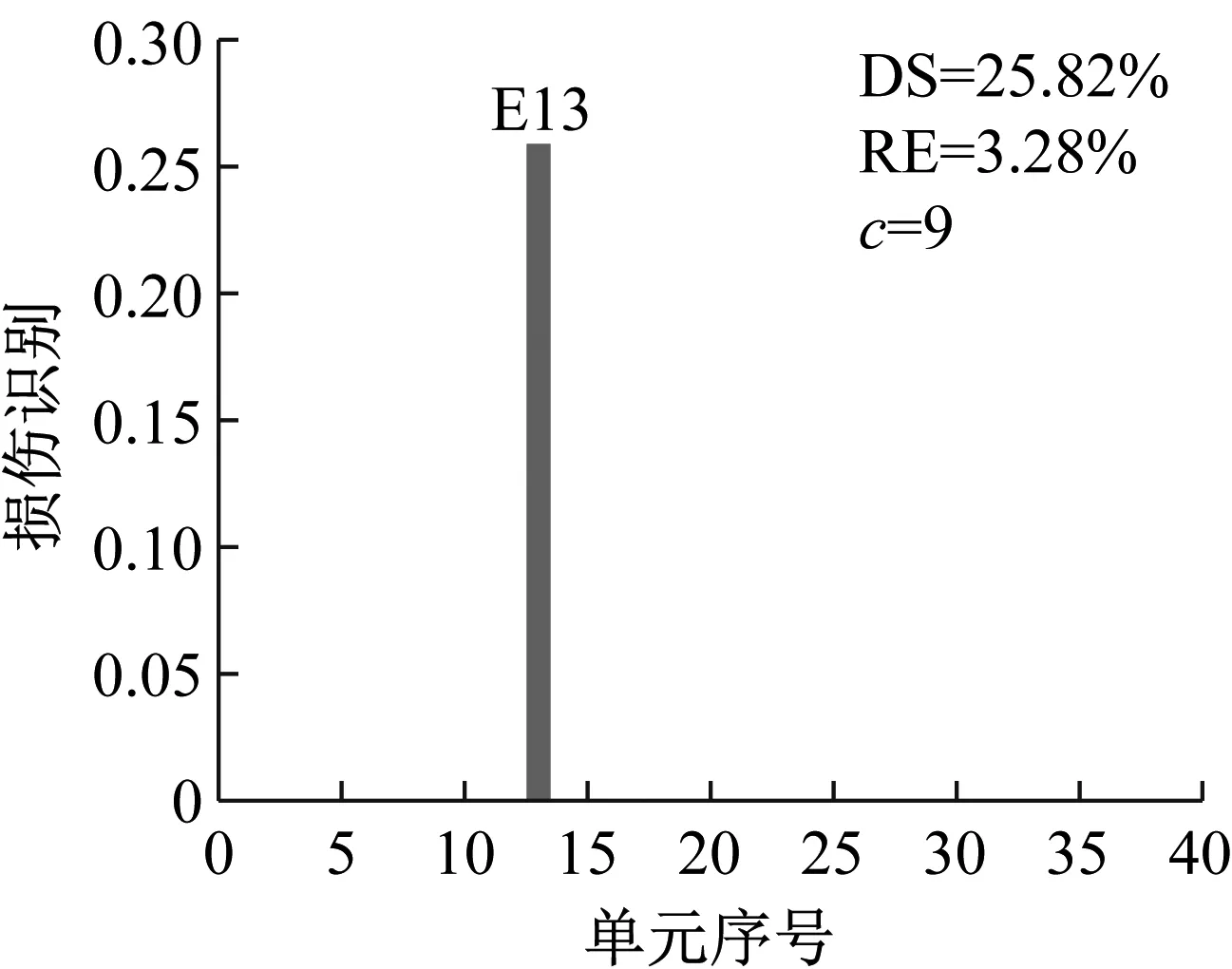
(b) CMSE-TRIM

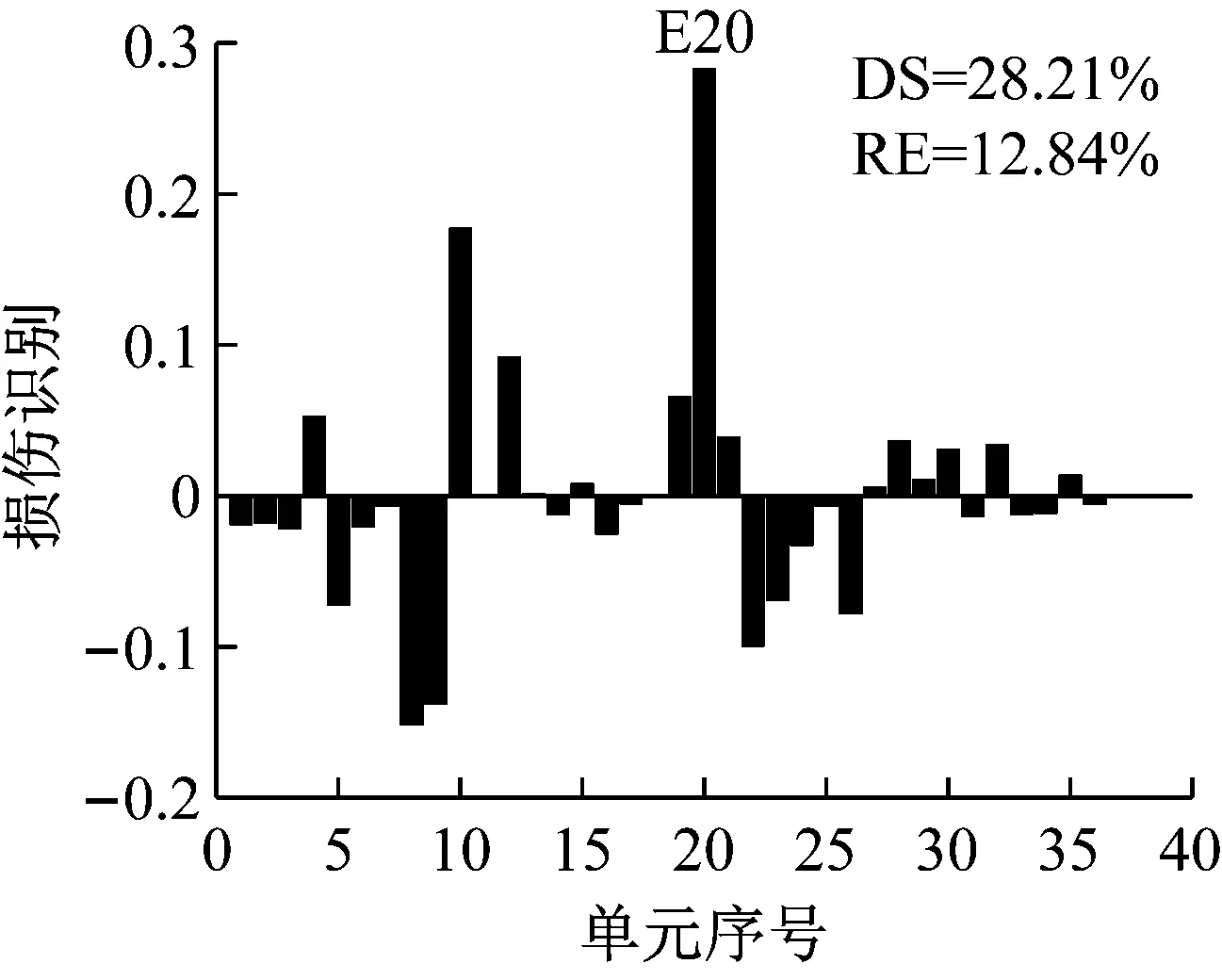
(a) CMSE-Tikhonov

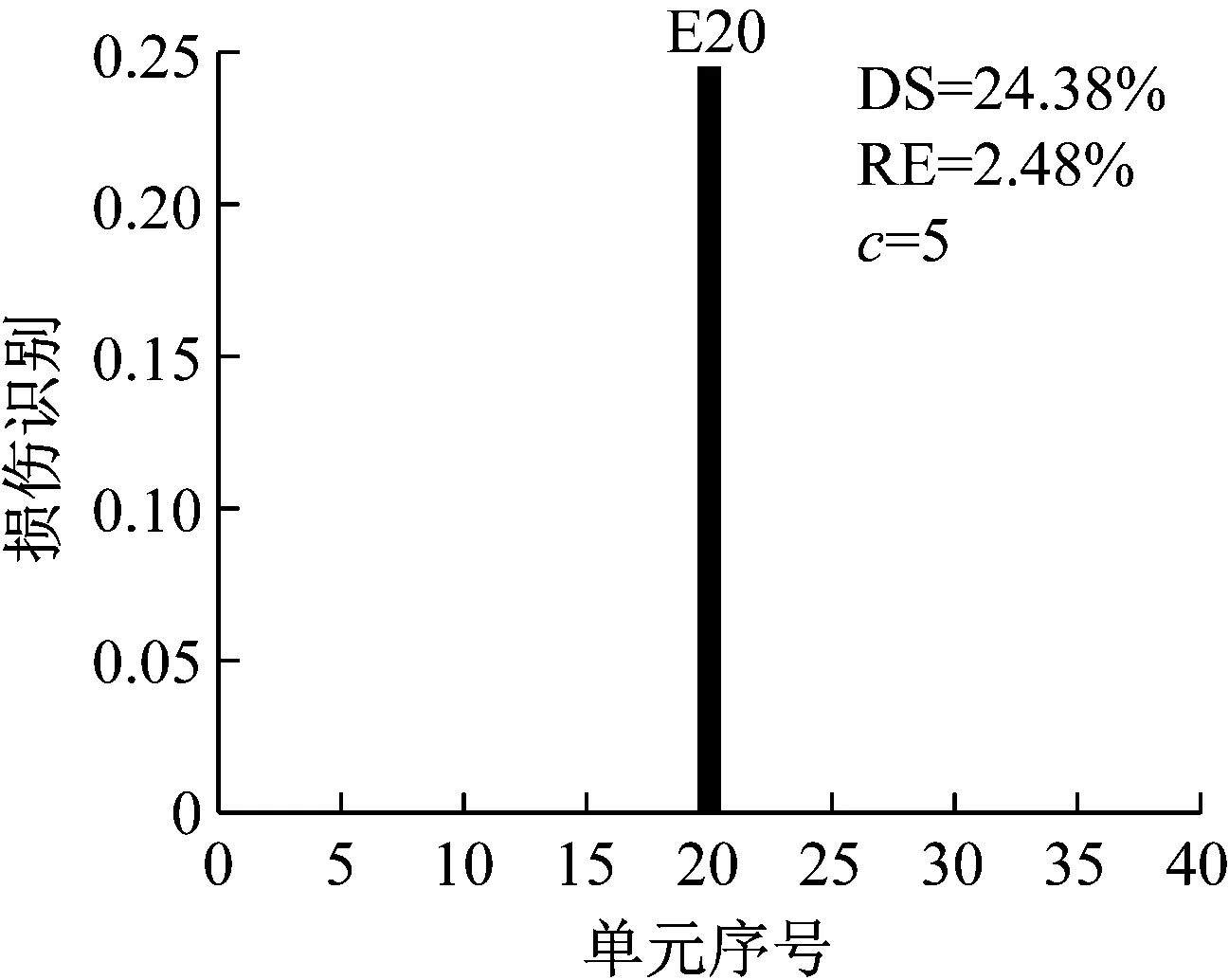
(b) CMSE-TRIM

(a) CMSE-Tikhonov

(b) CMSE-TRIM

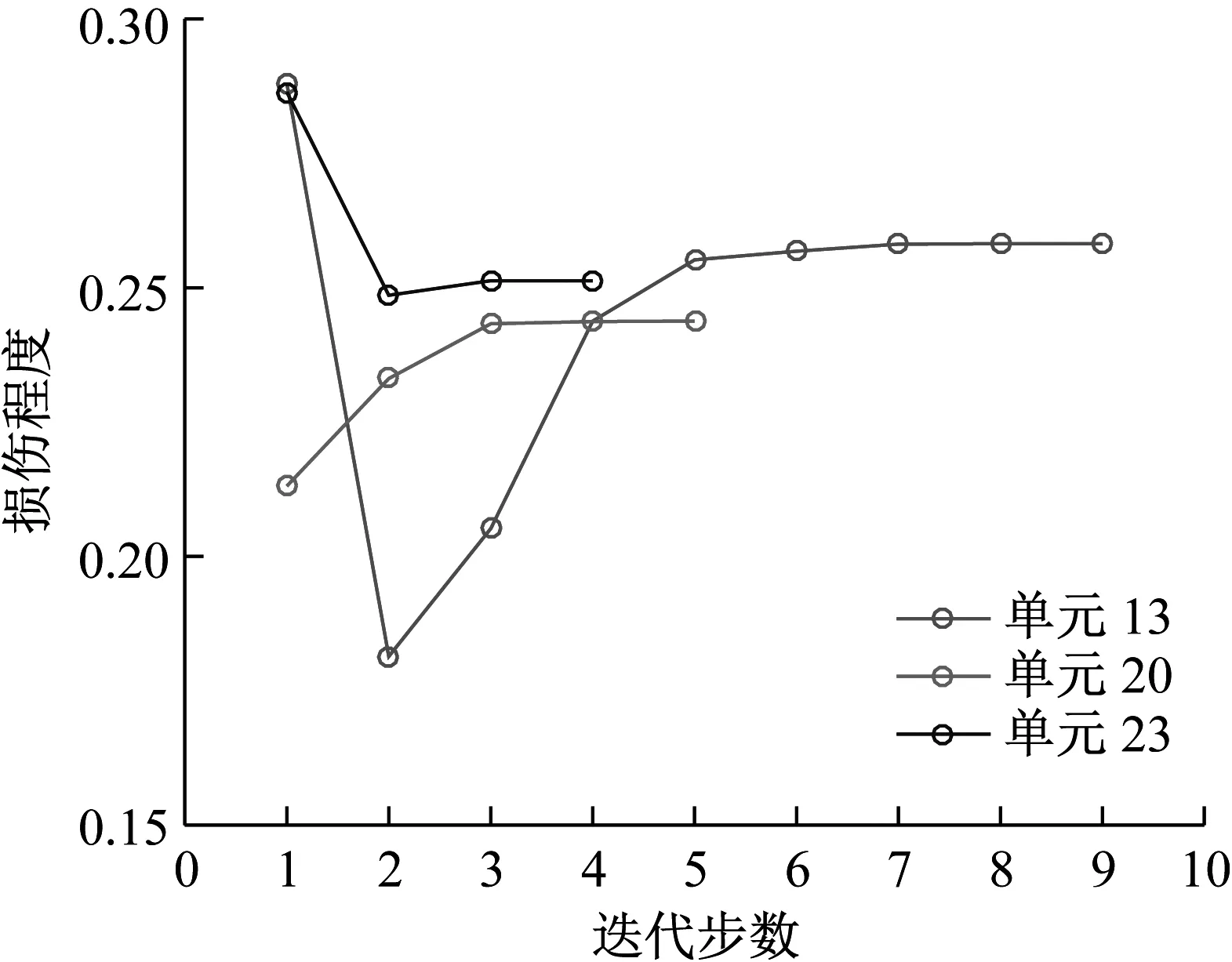
圖8 各損傷單元不同迭代步的損傷程度計算結果

4.2 損傷程度敏感性

設置噪聲水平1%，損傷單元23，選用結構損傷后1～3階模態，研究損傷方法對不同損傷程度(工況D1：5%，工況D2：15%，工況D3：25%)的損傷識別效果。兩種方法識別結果如圖9～圖11所示。

由圖9～圖11可以看出，當單元的損傷程度較小時，使用CMSE-Tikhonov方法會出現大量的虛假損傷掩蓋真實的損傷信息，從而無法完全損傷檢測；隨著損傷程度的增加，求解結果中的干擾項逐漸減少，損傷程度識別誤差也逐漸減小。相比之下，CMSE-TRIM對三種不同損傷程度的工況均能正確識別出損傷單元的位置，而且沒有出現虛假損傷。在損傷程度識別方面，CMSE-TRIM的識別誤差明顯小于CMSE-Tikhonov方法。此外，從計算所需的迭代次數上可以看出，在其他影響因素相同的條件下，TRIM方法需要較多的迭代次數來計算小損傷工況。

4.3 噪聲水平敏感性

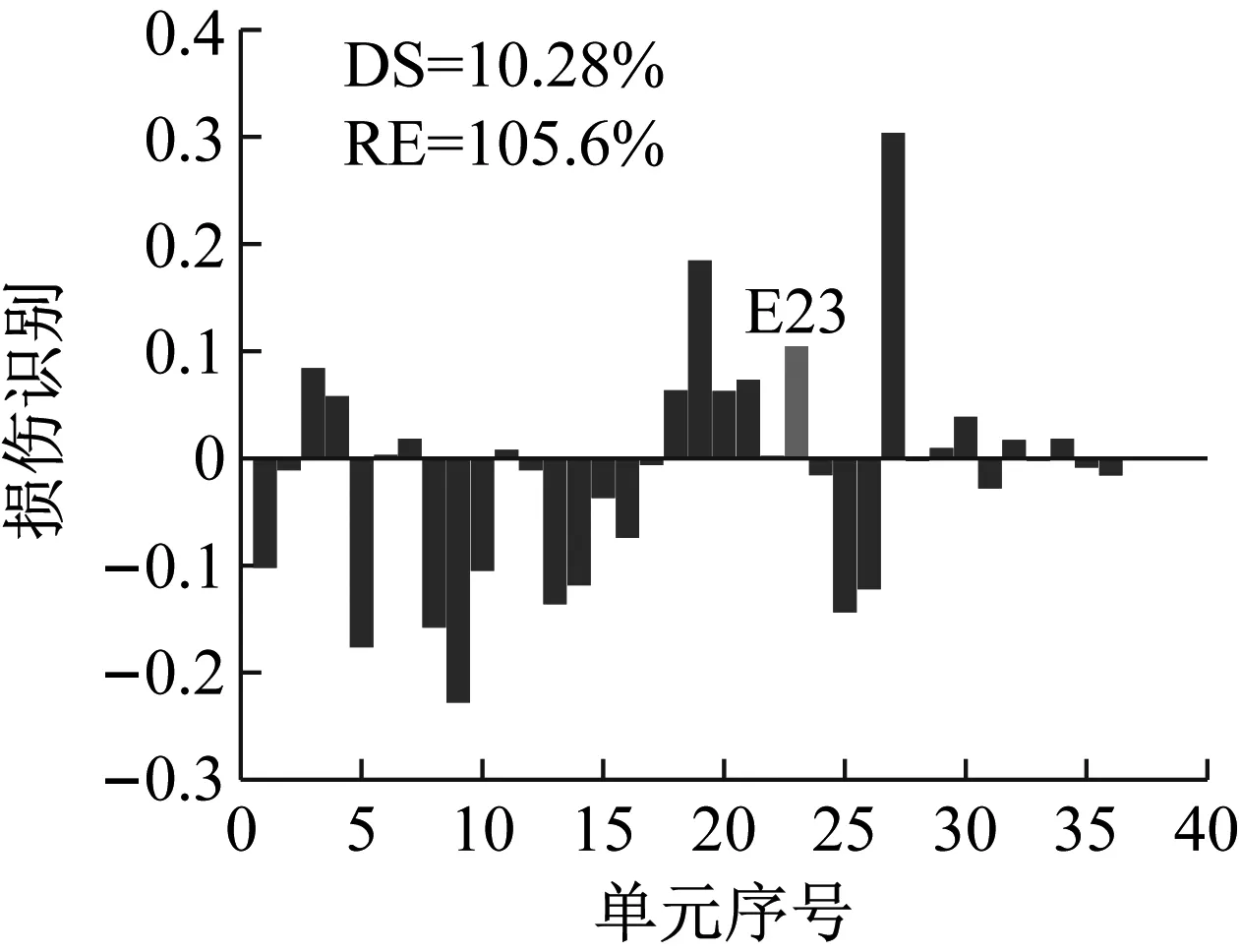
設置損傷單元23，損傷程度25%，選用結構損傷后1～3階模態，研究損傷方法在不同噪聲水平(工況N1：1%，工況N2：3%，工況N3：5%)下的損傷識別效果。識別結果如圖12～圖14所示。

分析圖12～圖14可以看出，當噪聲水平相對較低時，使用CMSE-Tikhonov方法能夠較好地識別出損傷位置及損傷程度，干擾項較少。隨著噪聲水平的提高，該方法損傷識別效果逐漸變差：在損傷定位方面，虛假損傷干擾項逐漸增多，掩蓋了真實的損傷信息；損傷程度識別誤差也逐漸增大。與之相比，CMSE-TRIM在不同噪聲水平影響下均能正確判定出損傷位置，不摻雜任何虛假損傷，而且損傷程度識別精度明顯高于CMSE-Tikhonov。此外，從計算所需的迭代次數上可以看出，在其他影響因素相同的條件下，當影響實測模態的噪聲水平提高時，TRIM方法計算所需的迭代次數相應增加。

(a) CMSE-Tikhonov

(b) CMSE-TRIM

(a) CMSE-Tikhonov

(b) CMSE-TRIM

(a) CMSE-Tikhonov

(b) CMSE-TRIM

(a) CMSE-Tikhonov

(b) CMSE-TRIM

(b) CMSE-TRIM

(a) CMSE-Tikhonov

(b) CMSE-TRIM

4.4 模態階數敏感性

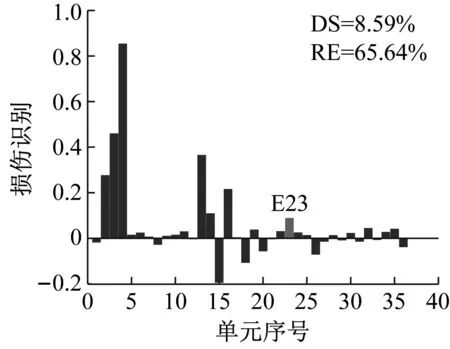
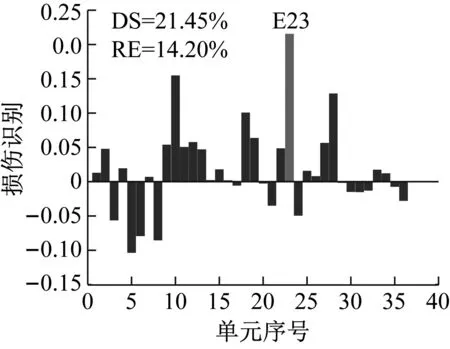
設置噪聲水平1%，損傷單元23，損傷程度25%，研究使用結構損傷后不同階數模態(工況M1：1，工況M2：1～2，工況M3：1～3)的損傷識別效果。兩種方法識別結果如圖15～圖17所示。

從圖15～圖17可以看出，當取用的損傷后模態只有第1階時，使用CMSE-Tikhonov和CMSE-TRIM都無法完成損傷識別；當取用的損傷后模態為前2階時，CMSE-Tikhonov方法雖然能夠識別出23號單元發生損傷，但是求解結果中摻雜多處虛假損傷干擾項，損傷程度求解誤差為14.20%；當取用的損傷后模態為前3階時，CMSE-Tikhonov求解結果中干擾項明顯減少，損傷程度識別精度有所提高。相比之下，當取用的損傷后模態為前2階或前3階時，CMSE-TRIM方法均能正確判定出損傷位置，不摻雜任何虛假損傷，而且損傷程度識別精度明顯高于CMSE-Tikhonov。此外，從計算所需的迭代次數上可以看出，在其他影響因素相同的條件下，取用的損傷后模態階數越多，TRIM方法計算所需的迭代次數越少。

(a) CMSE-Tikhonov

(b) CMSE-TRIM

(a) CMSE-Tikhonov

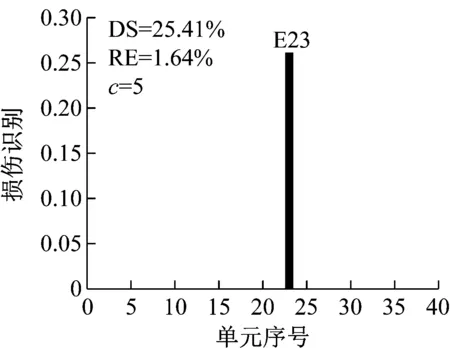
(b) CMSE-TRIM

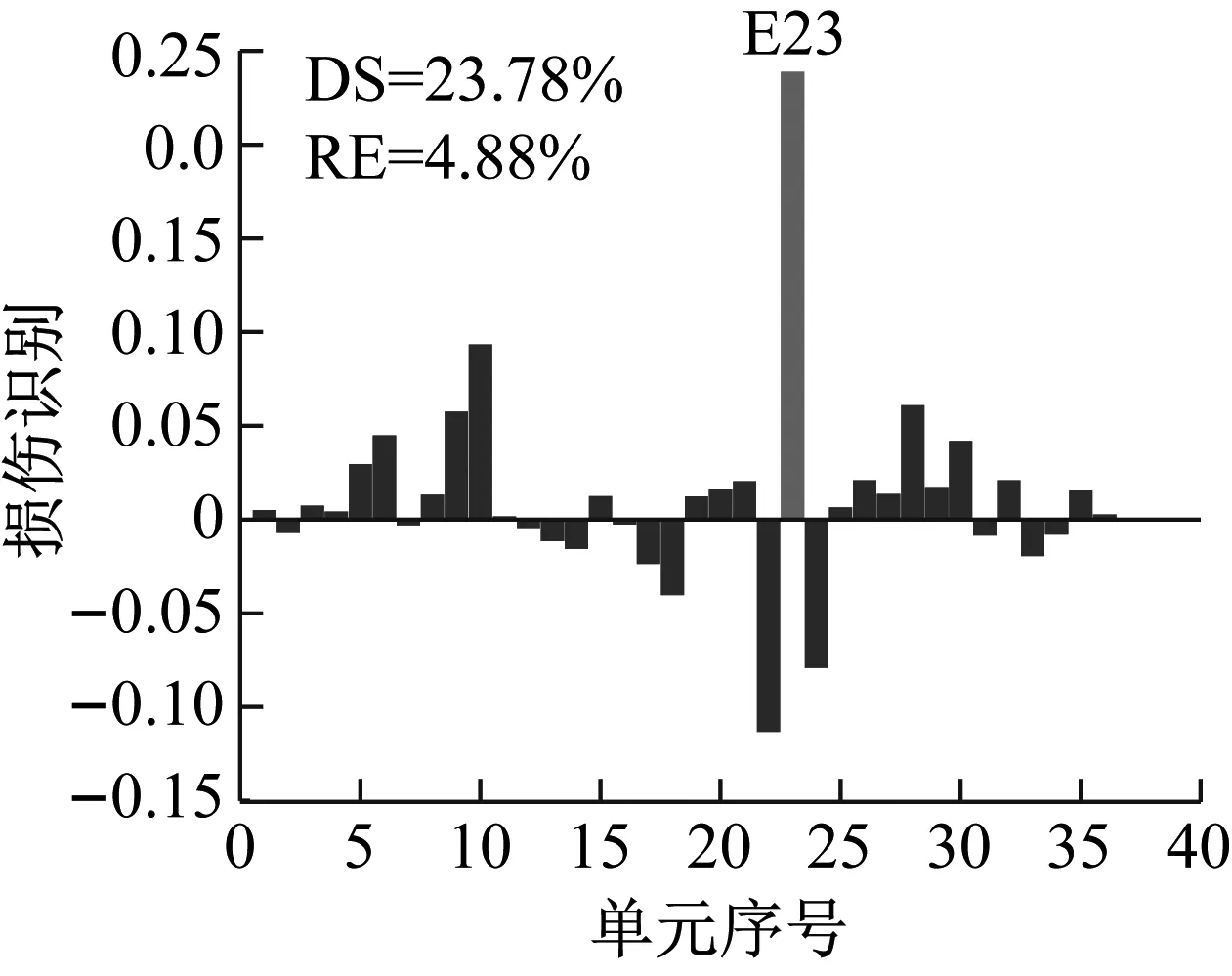
(a) CMSE-Tikhonov

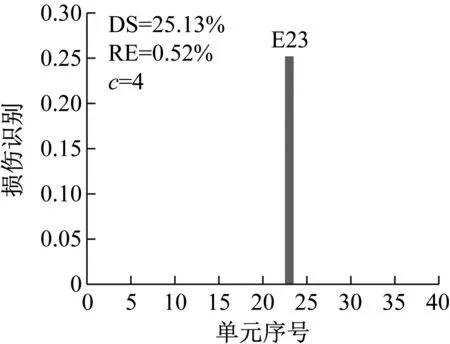
(b) CMSE-TRIM

5 結 論

針對測量噪聲影響下損傷檢測“病態”方程組的求解問題進行了研究，提出了一種基于Tikhonov正則化的迭代求解方法來抑制測量噪聲對損傷檢測的影響。選取一個海洋平臺結構開展數值模擬，探討了新方法在不同因素(損傷位置，損傷程度，噪聲水平，取用模態階數)影響下的損傷識別效果，并同傳統Tikhonov正則化求解下的損傷檢測進行了對比，結論如下：

傳統的Tikhonov正則化方法和本文提出的基于Tikhonov正則化的迭代求解方法均能在一定程度上解決噪聲影響下“病態”方程組的求解問題。相對于傳統的Tikhonov正則化求解方法，本文方法能夠有效地抑制虛假損傷、不遺漏真實損傷，具有更好的噪聲魯棒性。此外，本文方法直接選取方程組系數矩陣的中間奇異值作為初始正則化參數，通過迭代來自適應調整正則化參數及矩陣，無需通過大量試算來繪制L曲線圖，減少了計算工作量。數值分析表明，CMSE-TRIM方法對海洋平臺結構不同類型及不同損程度的損傷工況均能正確地識別，具有較好的噪聲魯棒性。損傷位置不敏感、損傷程度較小、噪聲水平較高以及取用的模態階數較少都會增加損傷檢測的難度，相應地會增加TRIM方法的迭代計算次數。