一種可改善傳動穩定性的混合勵磁型磁齒輪研究

井立兵， 陳俊霖， 張 廷

(1.三峽大學 電氣與新能源學院，湖北 宜昌 443002； 2.湖北省微電網工程技術研究中心(三峽大學)，湖北 宜昌 443002)

機械齒輪作為一種主要的傳動方式廣泛應用于工業生產中，但由于輪齒間相互接觸不可避免產生摩擦、噪音、振動等問題，而磁齒輪利用磁場間相互耦合實現轉矩傳遞，較機械齒輪具有無接觸、低噪聲、無需潤滑和自動過載保護等優勢[1-3]。

20世紀初美國學者提出了磁齒輪的概念并申請專利，從此開啟了磁場傳動的先例[4]。由于早期磁齒輪拓撲結構單一、永磁材料性能低、永磁體利用率很低，磁齒輪并未受到太多關注。直到Atallah和Howe提出基于磁場調制原理的同軸式磁齒輪[5]，磁齒輪才受到研究人員的重視。此后一段時間內，直線式[6]、聚磁式[7]和軸向式磁齒輪[8]相繼問世。眾所周知，Halbach陣列具有良好的正弦氣隙磁通密度分布和自屏蔽磁化特性。文獻[9]中提出了一種Halbach同軸式磁齒輪，通過仿真表明，Halbach陣列能大幅度減少氣隙磁通諧波含量，增加輸出轉矩。文獻[10]利用二維全局解析法推導了Halbach陣列同軸磁齒輪的氣隙磁場分布，并研究其參數與輸出轉矩間的關系。文獻[11]提出了一種新型雙通量調制器同軸磁齒輪，旨在提高永磁體利用率和輸出轉矩。目前，對于改善氣隙磁場、增大磁齒輪轉矩密度的研究已有很多，而致力于減少轉矩脈動，提高磁齒輪傳動穩定性還需進一步研究。

針對磁齒輪氣隙磁密諧波畸變率高和傳動穩定性差的問題，本文提出了一種改善內層氣隙磁密分布的偏心表貼式磁極結構，并在外轉子軛部開槽加入勵磁電流以降低磁齒輪轉矩脈動。利用有限元法對傳動比為6.75∶1的傳統型、開槽未加電流型和開槽加電流型磁齒輪氣隙磁場和轉矩脈動進行分析與計算，通過仿真表明，偏心磁極能實現對磁齒輪內層氣隙磁密的優化，氣隙磁密諧波畸變率明顯減小，另外施加勵磁電流能使磁齒輪具有更好的傳動穩定性。

1 工作原理

圖1為開槽加電流型磁齒輪的結構模型，主要包含內轉子、調磁環和外轉子三部分，調磁環對內、外氣隙磁場進行調制，從而實現轉矩傳遞。

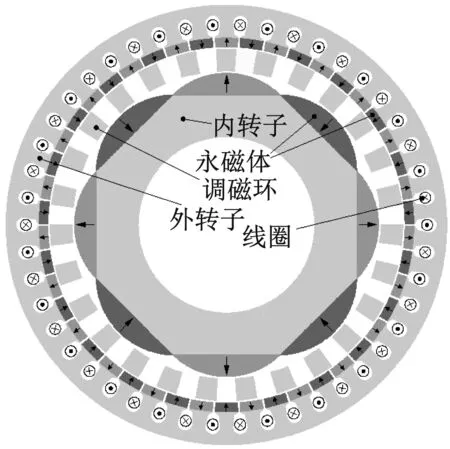
圖1 開槽加電流型磁齒輪模型

在不考慮調磁環作用下，氣隙內r處的徑向磁感應強度可表示為[12]

(1)

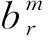
在引入調磁環后，調磁環的徑向調制函數可表示為

(2)

由此可得出經調磁環調制后氣隙的徑向磁感應強度為

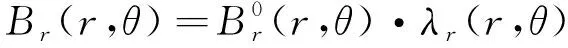
(3)

由文獻[13]可知，磁齒輪氣隙磁場所含的空間諧波極對數表示為

pm,k=|mp+kns|

(4)

式中:m=1,3,5,…,∞，k=0,±1,±2,…,∞；ns為調磁環的鐵心數量。

氣隙中的諧波分量具有特定的空間極對數和轉速，由文獻[14]可知，內、外層氣隙空間諧波分量的角速度表示為

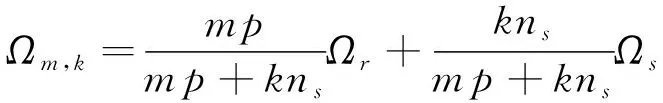
(5)

式中：Ωm,k為空間諧波分量的角速度，Ωr為內、外轉子的角速度，Ωs為調磁環的角速度。

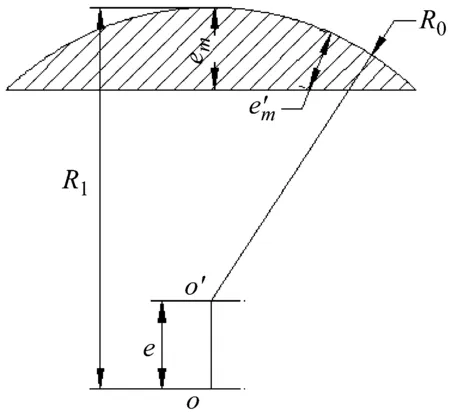
圖2 偏心永磁體

2 磁場分析

磁齒輪由內轉子、調磁環和外轉子三部分組成，內、外轉子上均有表貼式磁極，磁極對數按照傳動比分配。在本文中外轉子上通有勵磁電流不便于旋轉，因此，以下的研究均指外轉子充當定子固定不動，調磁環和內轉子旋轉，因此傳動比指調磁環極對數和內轉子極對數之比。另外，本文沒有對偏心系數進行深入研究，保證永磁體用量、內層氣隙的最短距離和傳統型參數相等的情況下，建立傳動比為6.75∶1的傳統型、開槽未加電流型和開槽加電流型的磁齒輪模型，表1給出了具體的模型參數。

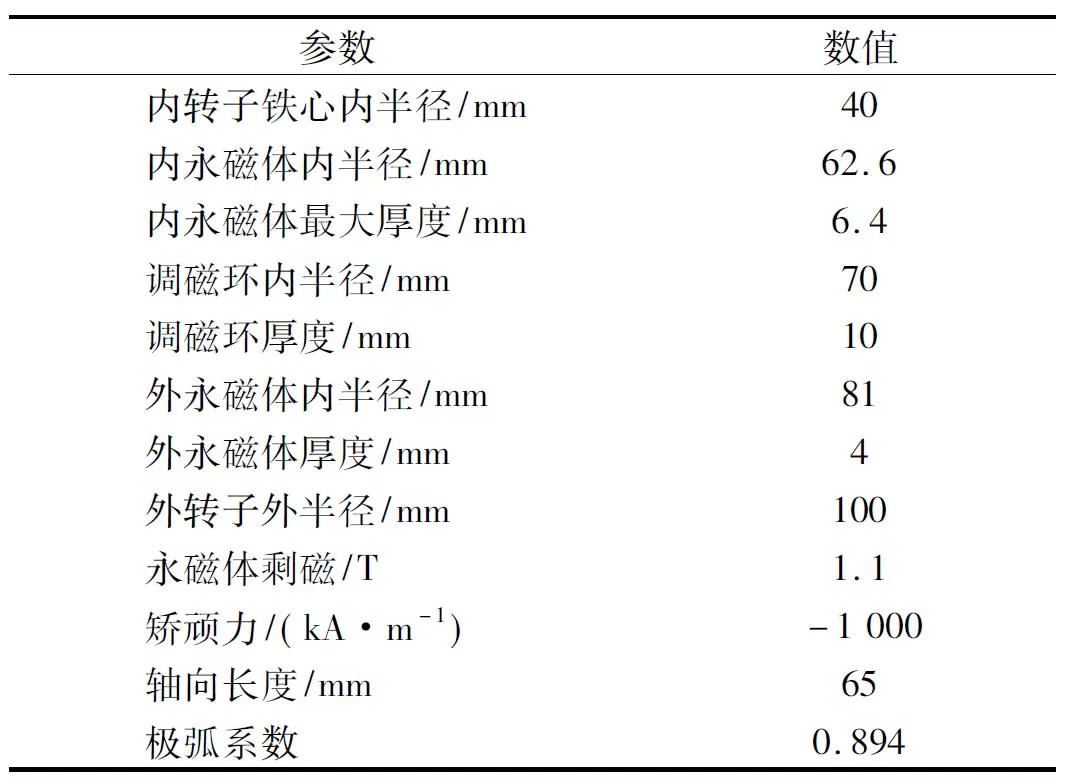
表1 磁齒輪參數

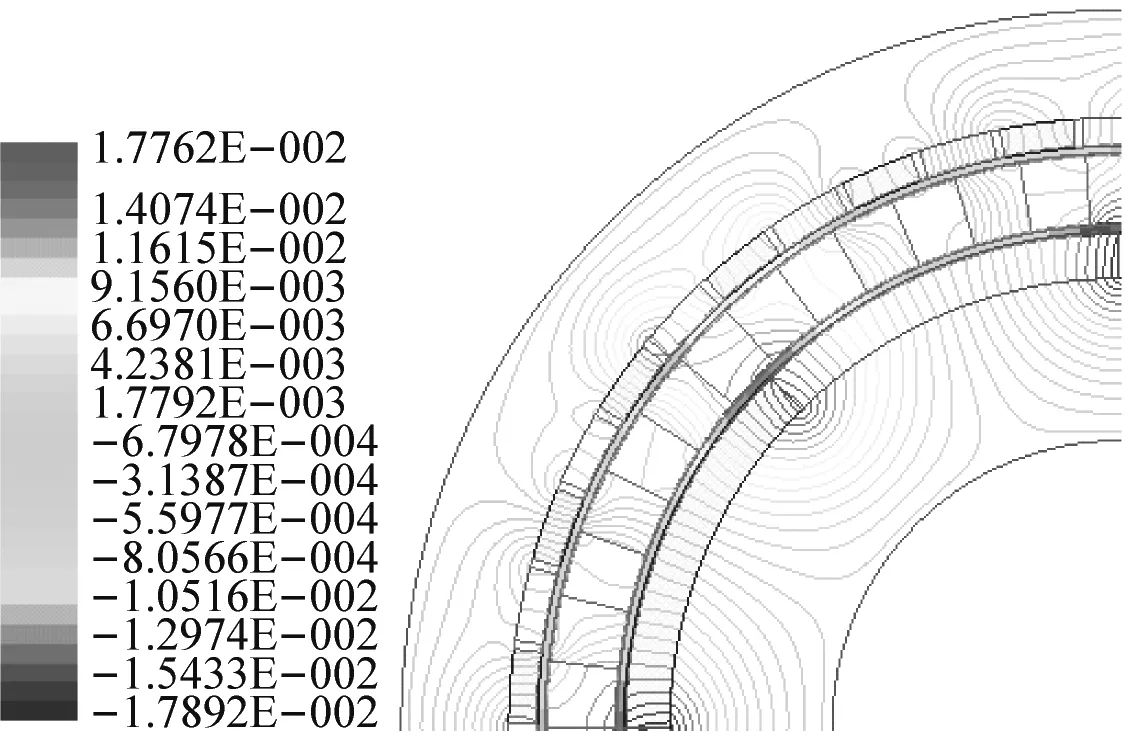
偏心結構的內永磁體使得內層氣隙不均勻，外層氣隙則為均勻氣隙。利用有限元ANSYS Maxwell軟件對氣隙磁場和電磁轉矩進行計算。圖3為傳統型、開槽未加電流型和開槽加電流型的磁力線分布情況。從磁力線對比圖可清晰的看出內轉子上有8個波頭，這與內轉子4對磁極相符。大量的磁力線從調磁環上的導體上穿過，非導體部分上有少量漏磁。開槽未加電流型和開槽加電流型減小部分外層氣隙磁場的通路，因此在槽的附近磁路相對易飽和。

圖4和圖5為三種磁齒輪的內、外層氣隙磁密分布圖。

(a) 傳統型

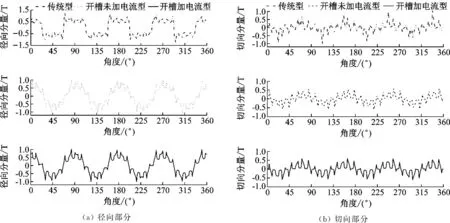
圖4 內層氣隙中間磁通密度

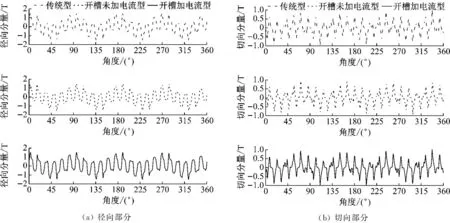
圖5 外層氣隙中間磁通密度

如圖4(a)和4(b)所示，改變內永磁體形狀，開槽未加電流型和開槽加電流型的磁齒輪與傳統磁齒輪相比，其內層氣隙磁密波形由矩形波變為正弦波，但兩者磁密徑向分量幅值由傳統型的1.25 T降到1 T。主要原因是偏心結構的圓弧狀磁極改變了內層氣隙長度，且由均勻氣隙變為不均勻氣隙。如圖5(a)和5(b)所示，傳統型、開槽未加電流型和開槽加電流型三者的外層氣隙磁密均沒有變化，徑向磁密幅值為1.5 T，切向磁密幅值為0.75 T，說明改變內永磁體形狀對外層氣隙磁密的影響較小。

圖6和圖7為磁齒輪內、外層氣隙磁密經傅里葉分解后的諧波對比圖。

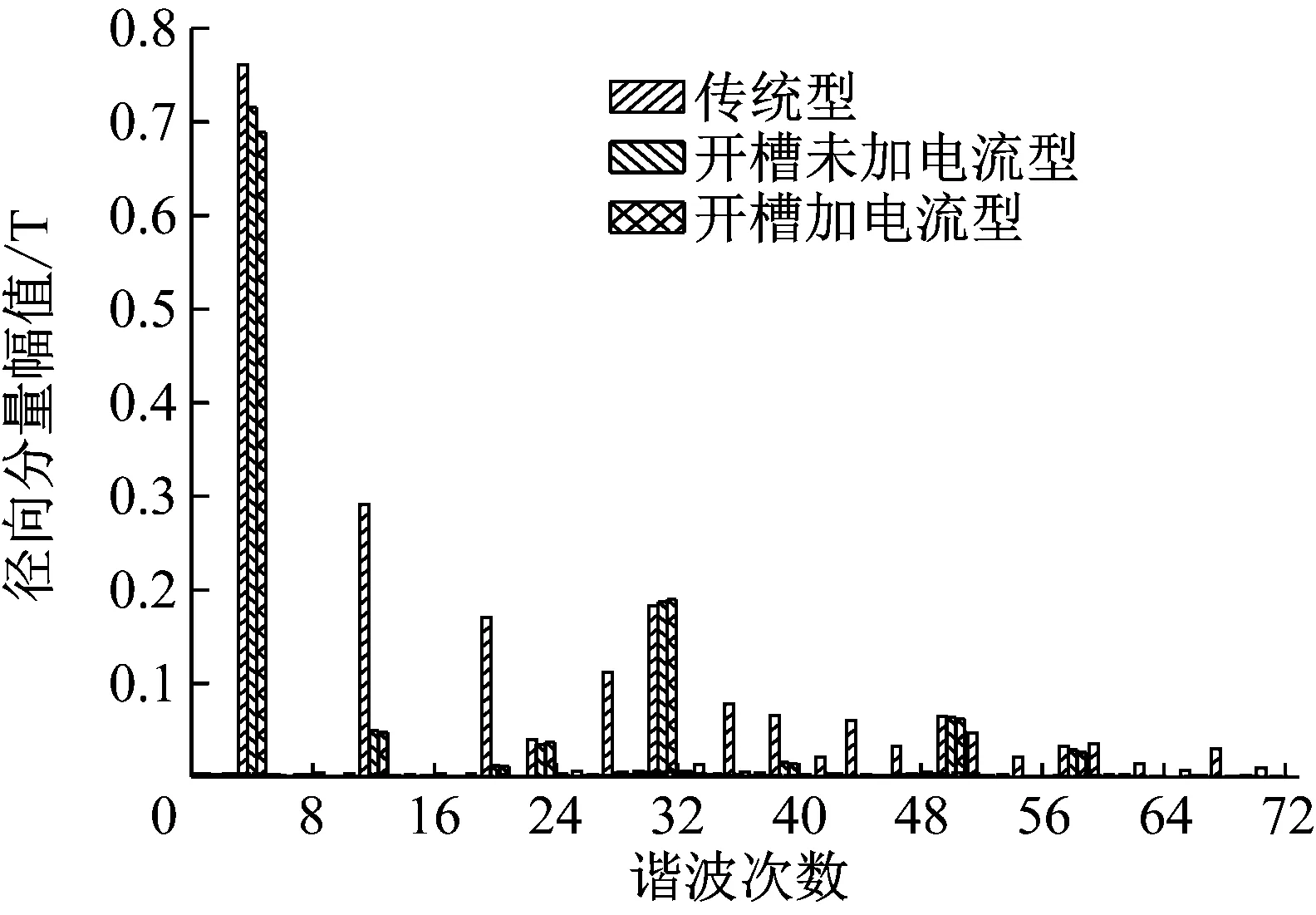
(a) 內層磁密徑向分量

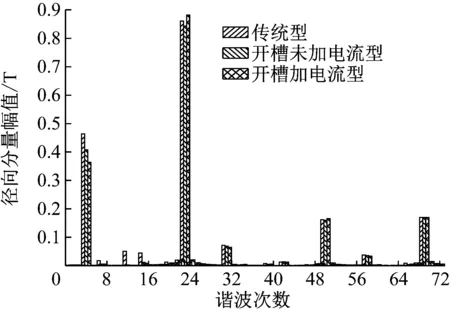
(a) 外層磁密徑向分量

如圖6(a)和6(b)所示，內層氣隙磁密不僅有基波，還有因調磁環的存在而引起的諧波。傳統型主要含有4、12、20、23、28、31、36、39、44和50次等諧波；改變內永磁體形狀后氣隙磁密諧波主要含有4、12、23、31和50次等諧波，相比傳統型，消除了20、28、36、39、44和50次等高次諧波，降低了諧波畸變率，有利于提高磁齒輪的傳動穩定性。如圖7(a)和7(b)所示，傳統型、開槽未加電流型和開槽加電流型三者的外層氣隙徑向諧波含量變化較小；對于外層切向諧波含量，開槽加電流型的4次和31次諧波幅值明顯大于另外兩者，31次諧波主要是由內永磁體的基波經調磁環調制出來的，說明改變永磁體形狀后有利于內、外磁場的耦合，從而增大轉矩的輸出。

3 電磁轉矩計算

靜態轉矩是衡量磁齒輪性能的重要參數，其值根據麥克斯韋張量法[15-18]可得

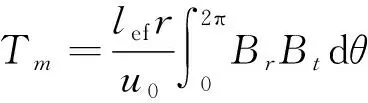
(4)

式中:lef為磁齒輪的軸向長度，Br和Bt為半徑為r處的徑向和切向磁密分量。

固定外軛鐵和調磁環，內轉子以675 r/min的速度逆時針轉動，從而得到內、外轉子靜態轉矩對比圖。如圖8所示。

從圖8中可看出，內、外轉子的靜態轉矩波形均為正弦波，并且在電角度為90°時達到最大值。從圖中看出開槽未加電流型較傳統型轉矩有所降低，主要是因為外軛鐵開槽降低了鐵的用量，從而減少了磁力線的回路。開槽加電流型比傳統型的轉矩更大一些，這是由于電流產生的磁場與永磁體自身磁場疊加增強了外層氣隙磁場。傳統型、開槽未加電流型和開槽加電流型三者的內轉子轉矩分別為29.44 N·m、27.35 N·m和29.62 N·m；外轉子轉矩分別為196.58 N·m、188.23 N·m和199.85 N·m。三者的傳動比分別為6.68∶1、6.88∶1和6.75∶1，傳統型和開槽未加電流型傳動比與理論傳動比分別相差1%和1.9%；而開槽加電流型的磁齒輪傳動比等于6.75∶1，從而也說明開槽加電流型的磁齒輪傳動穩定性更好。

固定外軛鐵和外永磁體，令內轉子和調磁環分別以675 r/min和100 r/min逆時針旋轉，從而得到內、外轉子的穩態轉矩如圖9所示。

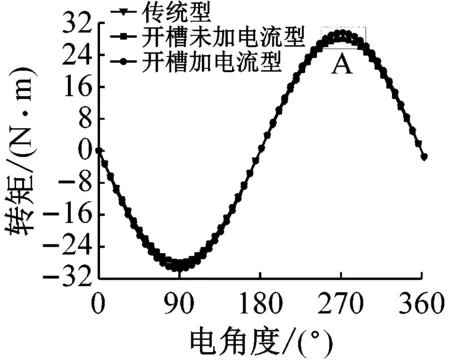
(a) 內轉子

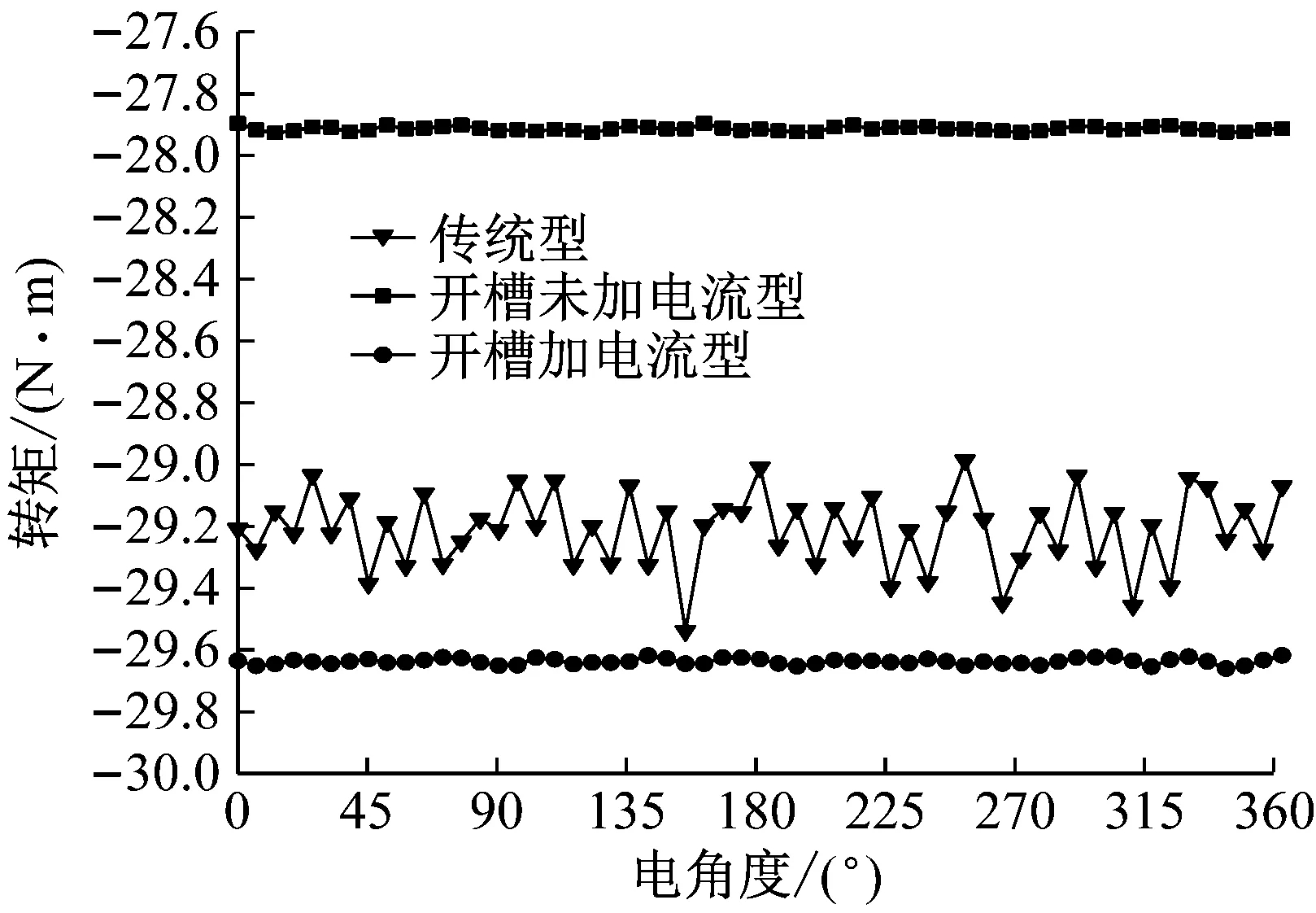
(a) 內轉子

從圖9中可以看出，傳統型的內轉子轉矩脈動明顯大于另外兩個模型；而外轉子的轉矩脈動則更小一些，這是由于外永磁體極對數多于內永磁體極對數。

表2列出了具體的傳統型、開槽未加電流型和開槽加電流型的磁齒輪轉矩脈動百分比。

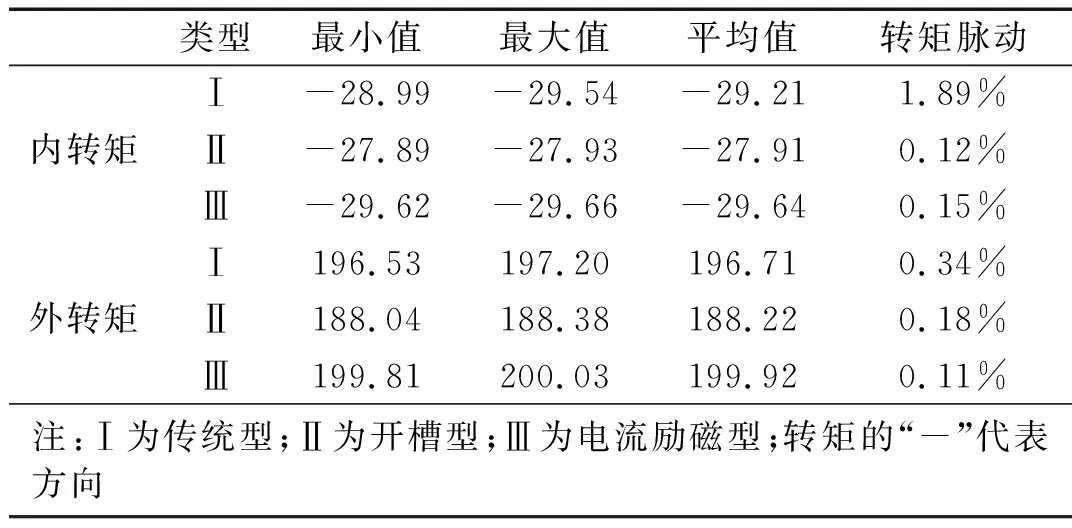
表2 轉矩脈動

從表2中可以看出，無論是內轉矩還是外轉矩，傳統型的轉矩脈動均大于另外兩種，而開槽加電流型的磁齒輪不僅可以提高傳動穩定性，相比開槽未加電流型的磁齒輪，也能提高輸出轉矩。開槽加電流型比傳統型的內、外轉子輸出轉矩分別提高了1.46%和1.63%；相對開槽未加電流型，分別提高了6.18%和6.22%。

表3為磁齒輪內層氣隙徑向諧波畸變率。

表3 氣隙諧波畸變率

從表3得知，傳統型結構的氣隙諧波畸變率最大，為56.97%，開槽加電流型次之，開槽未加電流型的諧波畸變率最小。考慮開槽加電流型較開槽未加電流型轉矩提高較多，諧波畸變率相差不大，因此開槽加電流型的磁齒輪較具有良好的轉矩性能和較高的傳動穩定性。

4 結 論

本文采用二維有限元法計算了傳統型、開槽未加電流型和開槽加電流型磁齒輪的磁場分布和電磁轉矩。通過比較內、外層氣隙磁密、諧波含量、轉矩波動發現，偏心永磁體結構有利于改善減內層磁密波形，諧波畸變率較傳統型大大降低，提高磁密的正弦度；其次，施加勵磁電流不僅能增大磁齒輪的輸出轉矩，還能降低轉矩波動，為改善磁齒輪的傳動穩定性提供了一種方法。