氣體泄漏聲源的時域壓縮波達方向估計研究
韋 娟, 鄭柳青, 鄭浩南, 王文靜, 寧方立
(1.西安電子科技大學 通信工程學院,西安 710071; 2.西北工業大學 機電學院,西安 710072;3.東莞市三航軍民融合創新研究院,東莞 523808)
氣體泄漏不僅會造成嚴重的經濟損失和能源浪費,還會給人民的生命財產安全帶來巨大危害[1],因此對氣體泄漏聲源的檢測和定位至關重要。氣體泄漏產生的聲波頻帶較寬,從可聽聲范圍到超聲范圍均有分布。其中在低頻段噪聲能量較大,因此一般取氣體泄漏聲波能量大而噪聲能量小的超聲頻段進行研究[2-3]。目前人們多利用聲源的超聲特性,用手持超聲檢測設備來獲得泄漏源位置,但其難以實現全面實時的檢測[4-5]。因此,學者開始研究采用麥克風陣列進行氣體泄漏聲源的DOA估計。
目前基于麥克風陣列的氣體泄漏聲源DOA估計算法,普遍存在采樣率高、數據量大以及計算復雜度高等缺點。文獻[6]根據分布式超聲換能器對氣體泄漏聲源進行檢測定位,其中每個傳感器均需以非常高的采樣速率采樣大量數據,并將這些數據傳輸至后臺進行處理。文獻[7]通過麥克風陣列檢測泄漏所產生的低于20 kHz的聲波,利用波束形成方法得到泄漏聲源的DOA估計,然而該方法所檢測的是可聽聲頻段,在該頻段內背景噪聲較強,會將泄漏噪聲淹沒,導致該方法失效。文獻[8]利用隨機部署的平面麥克風陣列,通過稀疏表示方法進行氣體泄漏聲源的方位估計。文獻[9]應用9個MEMS麥克風構成“T”型陣列,采用波束形成方法得到氣體泄漏聲源的DOA估計。上述方法中所有麥克風均為高速率采樣,導致硬件的配置難度增加以及巨大的計算量,因而在實際應用中受到一定限制。
壓縮感知[10-12]技術利用信號的稀疏性,通過少量的采樣數據即可重構原始信號,極大地降低信號的采樣速率以及數據的存儲量和計算量,現已廣泛應用于寬帶信號采集與處理、圖像處理、數據壓縮等諸多領域。壓縮感知理論提出之初主要針對離散數字信號,后來學者相繼提出了基于壓縮感知理論的模擬信號的直接信息采樣方法[13-15],但都存在一定的局限性。例如調制寬帶轉化器的采樣結構適合處理寬頻帶模擬信號,但其主要針對的是稀疏多帶信號。文獻[16]提出一種壓縮方位估計算法進行聲源的DOA估計。其設計思想是選用一個麥克風作為參考麥克風(Reference Microphone, RM)以高于奈奎斯特采樣率的速率進行高速采樣,其他麥克風進行壓縮測量,通過少量的測量數據,計算得到聲源DOA估計結果。然而該算法還是先將模擬信號高速率采樣得到離散信號后再處理,并沒有實現模擬信號的直接壓縮采樣;并且選擇隨機高斯矩陣作為測量矩陣,需要對矩陣的每個元素進行存儲和計算,復雜度較高;此外在信號重構時采用Dantzig選擇器[17]的求解方法,其參數選取對算法的影響較大,且計算復雜度較高。針對上述問題,本文提出一種基于時域壓縮的直接非均勻隨機欠采樣DOA估計算法,在不改變傳統采樣電路的前提下直接對氣體泄漏聲源信號進行低速隨機壓縮采樣,采用計算速度快、重構精度高的子空間追蹤(Subspace Pursuit, SP)算法,通過較少的采樣數據準確得到氣體泄漏聲源的DOA估計結果,極大減少了系統所需的存儲量與運算量。
1 基于壓縮感知的DOA估計數學模型
基于壓縮感知的聲源DOA估計多在頻域上實現,其特點是聲源信號可以通過一些主要的頻率分量表征[18]。而氣體泄漏聲源是一種寬頻帶且具有復雜頻譜結構的超聲波,不具有頻譜稀疏性。因此,本文采用時域方法進行研究。
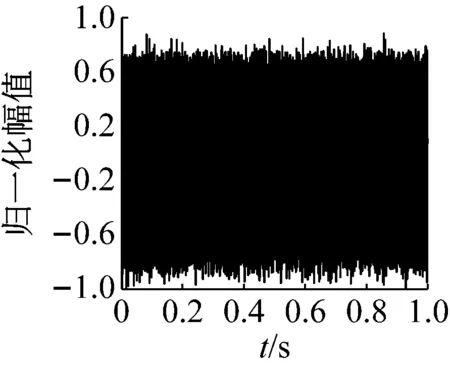
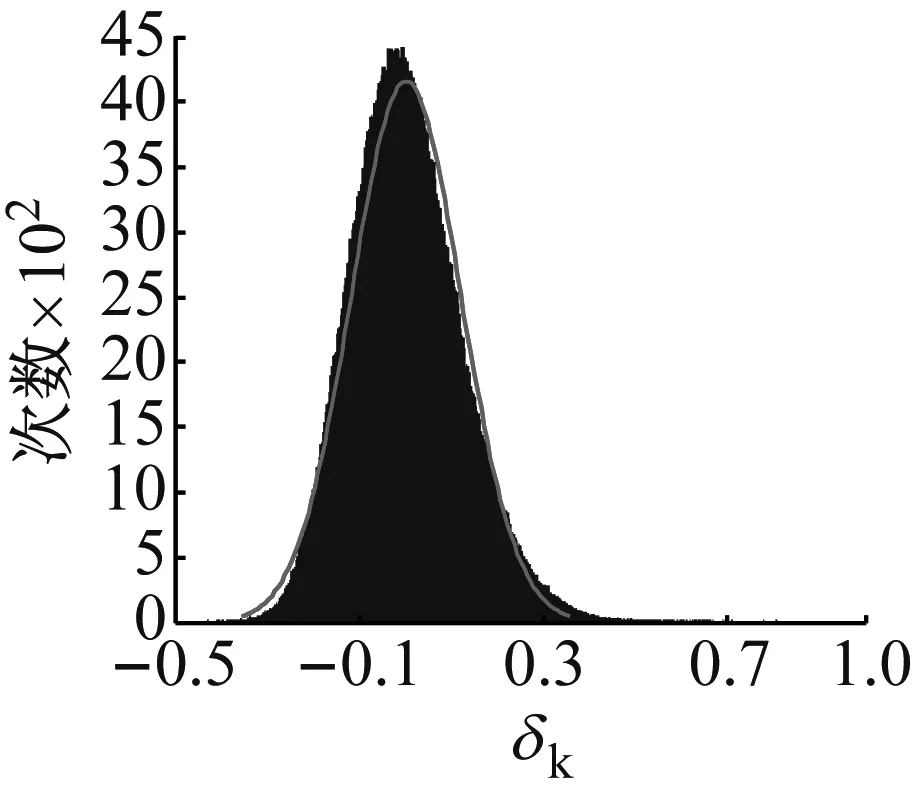
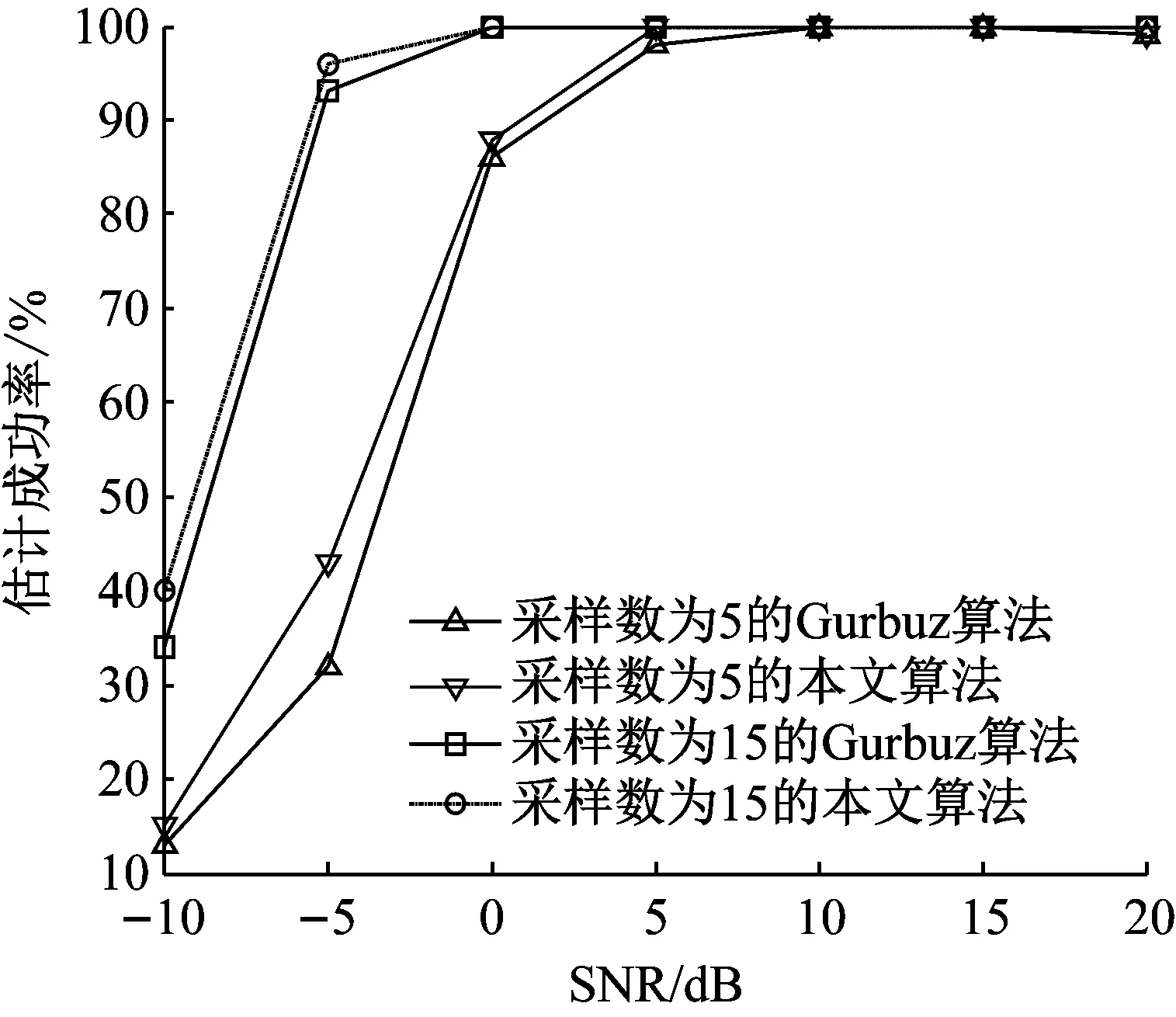
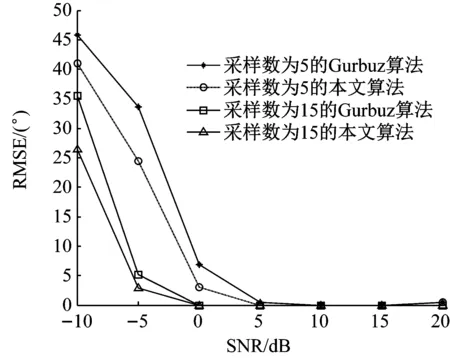
假設一維空間內有K個氣體泄漏聲源,均為遠場聲源。將空間等角度劃分為N份,即B={θ0,θ1,…,θΝ},其中K< 遠場聲源DOA估計示意圖如圖1所示,麥克風陣列為均勻線陣,陣元數目為L,陣元間距為d。其中,RM以高于2倍奈奎斯特采樣率的采樣頻率進行標準采樣,其余麥克風作為壓縮采樣麥克風進行壓縮采樣。 圖1 遠場聲源DOA估計示意圖 t時刻,RM接收到的聲源信號為 ζRM(t)=wsk(t+r0/c) (1) 式中:sk(t)為第k個聲源信號,w為信號幅度的衰減系數,r0表示聲源與陣列的間距,c表示聲速。 第i個壓縮采樣麥克風接收到的聲源信號為 (2) (3) RM以高采樣率對聲源信號進行采樣,可以表示為 (4) 式中:t0為RM采樣的起始時刻,Fs為RM的采樣頻率,Nt為RM的采樣數目。 在實際應用中,氣體泄漏聲源信號未知,若對RM以較高的采樣率采樣便可近似為聲源信號。假設第i個壓縮采樣麥克風以Fs的采樣頻率進行采樣,那么第i個壓縮采樣麥克風的采樣數據矢量為 (5) ζi=Dib (6) 式中:Di為Nt×(N+1)維矩陣,表示第i個壓縮采樣麥克風對應的冗余字典。為了更好理解,將冗余字典的第j列給出 (7) 因此,基于壓縮感知的聲源DOA估計數學模型可表示為 β=ΦDb+e=Ab+e (8) 本節提出一種對模擬信號直接壓縮采樣方案,通過設計一種低速非均勻采樣時鐘,在對應的采樣時刻以遠低于奈奎斯特采樣率的采樣頻率對模擬信號直接壓縮采樣。所提出的直接非均勻隨機欠采樣方案除了需要設計采樣時鐘外,傳統采樣電路的其他部分不必重新設計。低速非均勻采樣時鐘的設計要保證采樣點在采樣時段內分布平衡,即不能出現在某一段時間內采樣間隔很小但采樣點數較多,而在另一段時間內采樣間隔很大但采樣點數較少,否則采集到的信息不全面;此外,任何采樣時間間隔均必須大于RM采樣的時間間隔,否則不能實現低速率采樣。所設計的采樣方案如圖2所示。 圖2 直接非均勻隨機欠采樣方案結構圖 RM是以Fs的采樣率進行均勻采樣,其采樣時間函數為 (9) 式中:tRM(1)表示RM第一個數據的采樣時刻,記為t0。Ts=1/Fs,表示RM采樣時間間隔。 壓縮采樣麥克風采樣時間函數為 (10) 式中:t(1)表示第一個采樣時刻,均為t0。M表示采樣數目,t(M)均等于RM的第Nt個采樣時刻。Tave為平均采樣時間間隔 (11) 式中:|·|表示下取整操作。um-1表示服從均勻分布的隨機數,且需滿足 um-1<(Nt-1)2(M-1) (12) 即um-1Ts<1/2Tave。 根據采樣方案設計有效的測量矩陣是一個難點,測量矩陣的構造直接影響了信號的重構精度。針對2.1節中提出的直接非均勻隨機欠采樣策略,構造與之對應的等效測量矩陣。分析第1節中冗余字典的建立,每個子冗余字典中的每一列都可以看作以Fs的采樣率對聲源信號進行的均勻采樣,而壓縮采樣麥克風對信號的隨機采樣可以看作是利用等效測量矩陣對冗余字典中的每一列進行隨機觀測。根據所設計的采樣策略,建立每個等效子測量矩陣的構造規則 (13) 其中, J(1)=1, J(M)=NtJ(m)=(m-1)(Nt-1)/(M-1)+um-1, m=2,…,M-1 (14) 設計的等效子測量矩陣每一行僅有一個元素為1,且位于不同列,其他元素均為0,矩陣非常稀疏且形式簡單。在其存儲過程中,僅需存儲元素為1的位置即可,極大地減少了存儲量;此外,在其運算過程中,由于矩陣元素只有0和1,從而避免了乘法和加法運算,極大減少了計算量。每個壓縮采樣麥克風對應一個子測量矩陣,根據式(13)和(14)構造L-1個等效測量矩陣,再將子測量矩陣融合成具有塊對角結構的等效測量矩陣。 壓縮感知的目標是在已知低維觀測信號β和A陣的情況下,先重構出稀疏模式矢量b,再計算得到原始信號ζ。重構算法作為壓縮感知的關鍵步驟之一,其優劣將直接影響到壓縮感知的性能。第1節給出了基于壓縮感知的聲源DOA估計數學模型,由于矢量b是稀疏的,因此式(8)可以轉化為最小l0范數問題,即: (15) 式中:ε表示與噪聲和測量誤差有關的參數。然而該優化問題屬于NP-Hard問題,不具有多項式時間內的解。針對式(15)的非凸問題求解,學者提出了利用l1范數代替l0范數的思想,將該問題轉化為二階錐規劃問題[19] (16) 文獻[16]將式(16)轉化為Dantzig選擇器問題 (17) 然而該方法計算復雜度較大,且參數γ值的選取對算法的影響也較大。基于此,我們采用貪婪算法中性能較好的SP算法對式(8)進行求解。 綜上所述,所提算法應用于氣體泄漏聲源DOA估計的步驟歸納為: 步驟1一維空間角度均勻劃分為180份,麥克風陣列布局為均勻線陣,陣元數目為L,任選一個麥克風作為RM,其他麥克風作為壓縮采樣麥克風。 步驟2RM以高于奈奎斯特采樣率的采樣頻率進行標準采樣,并根據式(5)建立冗余字典。 步驟3生成L-1組服從均勻分布的隨機數,根據式(10)設計的隨機非均勻欠采樣方案得到L-1組采樣時鐘,該時鐘用來確定壓縮采樣麥克風的采樣時刻;每組采樣時鐘的數目為M,即壓縮采樣麥克風的采樣數目。 步驟4每個壓縮采樣麥克風根據式(10)對應的采樣時刻對氣體泄漏聲源直接進行壓縮采樣,將其采樣數據組合成L-1個壓縮測量矢量。 步驟5根據式(13)和式(14)的采樣策略構造相對應的等效測量矩陣; 步驟6在已知冗余字典、壓縮測量矢量、測量矩陣和稀疏度的前提下,通過SP重構算法計算得到氣體泄漏聲源的DOA估計。 所提算法的原理框圖如圖3所示。 圖3 所提算法原理框圖 綜上可知,所提算法僅用一個麥克風作為參考麥克風對氣體泄漏聲源進行標準采樣,目的是為了構造冗余字典實現聲源信號的稀疏表示;壓縮采樣麥克風均是以遠低于奈奎斯特采樣率的采樣頻率對聲源信號直接壓縮采樣,降低了信號的采樣率,實現了對模擬信號的直接壓縮采樣。 衡量算法是否可行的一個重要指標就是算法復雜度。所提算法影響計算復雜度的因素主要在于測量矩陣及其參與運算帶來的計算量,為證明所提算法在計算復雜度方面的優勢,分別選取隨機高斯矩陣、隨機伯努利矩陣以及算法中構造的等效測量矩陣作為測量矩陣,比較不同測量矩陣下算法的計算復雜度。因為算法的運行時間主要取決于乘法和加法運算,因此用乘法和加法的運算次數表征每種算法的計算復雜度。文獻[16]中Gurbuz算法采用的測量矩陣是隨機高斯矩陣,其中每個元素均為隨機浮點數,并參與乘法和加法運算,因此耗費存儲空間較大,計算復雜度較高。對于由隨機伯努利矩陣構成的測量矩陣,其中每個元素都是+1或-1,所以不需乘法運算,僅需加法運算,相比于隨機高斯矩陣計算復雜度有所降低,但仍要存儲每個元素,耗費的存儲空間也較大。而所提算法設計的等效測量矩陣,只有少量元素為1,大多數元素為0,所以不需加法和乘法運算,且僅需存儲值為1的元素,所需存儲空間非常小。現給出不同子測量矩陣下算法的計算復雜度以及存儲空間分配情況,如表1所示。 表1 不同子測量矩陣下算法的計算復雜度和存儲空間分配 (a) 人為制造孔徑1.5 mm 利用蒙特卡洛方法,驗證所提算法中的A陣滿足約束等距性(Restricted Isometry Property, RIP)[20-21]條件。測量矩陣分別為Gurbuz算法采用的隨機高斯矩陣以及本文設計的等效測量矩陣。每種測量矩陣下仿真次數為106。 圖5給出了測量矩陣分別由隨機高斯矩陣和等效測量矩陣構成情況下的蒙特卡洛仿真結果。分析可知,等效測量矩陣作為測量矩陣時,有限等距常數δk的最大值為0.359 4,隨機高斯矩陣作為測量矩陣時,δk的最大值為0.356 1。由此可知,本文設計的等效測量矩陣和隨機高斯矩陣均能令A陣滿足RIP條件[22],且RIP性質近似,但相比于隨機高斯矩陣,等效測量矩陣在計算復雜度以及存儲空間分配方面具有明顯的優勢。 (a) 隨機高斯矩陣 為驗證本文算法的有效性,實驗采集同時有兩個泄漏孔時的氣體泄漏聲音信號,信號來向分別為60°和123°。每個壓縮采樣麥克風的采樣數目設定為20。圖6給出了所提算法對氣體泄漏聲源進行DOA估計的仿真結果,分析可知,一維空間角度僅在來波方向處出現峰值。表明所提算法能實現對氣體泄漏聲源的準確DOA估計,且估計效果良好。 圖6 氣體泄漏聲源DOA估計 為驗證本文算法在分辨率上的優勢,實驗采集同時存在兩個泄漏孔時的氣體泄漏聲音信號,信號來向分別為50°和51°。每個壓縮采樣麥克風的采樣數目設定為20。圖7給出了所提算法對兩個空間角度相近的氣體泄漏聲源進行DOA估計的結果。分析可知,所提算法能準確實現對空間角度相近的氣體泄漏聲源的DOA估計,且分辨率較高。 圖7 DOA估計分辨率 為驗證所提算法性能的優越性,參考文獻[7],將頻帶為20~80 kHz的高斯白噪聲作為氣體泄漏聲源,對壓縮采樣麥克風在不同采樣數目下的算法性能進行仿真分析。其中,采樣數目以間隔5增加,SNR以間隔5 dB增加。每種條件下均進行100次蒙特卡洛仿真實驗。圖8和圖9分別給出了不同采樣數目下DOA估計成功率以及RMSE隨SNR變化的曲線圖。分析可知,當-10 dB≤SNR≤0 dB時,采樣數目越多,氣體泄漏聲源的DOA估計成功率越高且RMSE越小。當SNR>0 dB時,除了采樣數目為5之外,其他情況下均能達到100%的DOA估計成功率,并且RMSE為0。而當SNR=5 dB時,即使采樣數目為5,也能得到100%正確的DOA估計結果。分析表明,所提算法能夠通過較少的采樣數據實現對氣體泄漏聲源準確的DOA估計,充分體現了其在壓縮采樣方面的優勢。 圖8 所提算法估計成功率與SNR關系 圖9 所提算法RMSE與SNR關系 為驗證所提算法對比于Gurbuz算法的優勢,現對兩種方法在相同采樣數目條件下的算法性能進行仿真分析。圖10和圖11分別給出了所提算法和Gurbuz算法的估計成功率及RMSE隨SNR變化的對比圖。分析可知,相同采樣數目下,所提算法在低SNR下的估計成功率和RMSE整體優于Gurbuz算法,進而說明其DOA估計性能的優越性。 圖10 估計成功率與SNR的關系對比 圖11 RMSE與SNR的關系對比 本文所研究的氣體泄漏聲源是一種寬帶超聲波,針對其頻譜特性以及現有算法的不足,提出了一種基于時域壓縮的氣體泄漏聲源DOA估計算法。首先設計一種直接非均勻隨機欠采樣方案,該采樣方案無需改變傳統采樣的硬件系統,只需重新設計采樣時鐘就能實現對聲源信號的直接壓縮采樣;然后構造相對應的等效測量矩陣,該等效測量矩陣中僅有少量元素為1,大多數元素為0,極大減少了數據量和計算復雜度;最后,通過SP重構算法計算得到氣體泄漏聲源DOA估計。通過所提算法的DOA估計性能進行仿真分析,結果表明所提算法在降低計算復雜度和數據存儲量的同時,提高了DOA估計準確率,充分驗證了所提算法的準確性與有效性。本文研究對于解決傳統氣體泄漏聲源DOA估計方法中普遍存在的采樣率高和計算量大的問題,以及有效降低數據傳輸、存儲和處理的成本,提高參數的估計性能提供了一定的研究意義與實際應用價值。

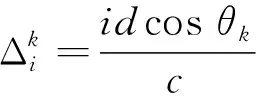


2 算法原理
2.1 直接非均勻隨機欠采樣方案



2.2 等效測量矩陣構造


2.3 重構算法
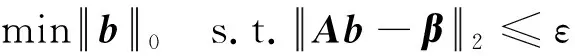
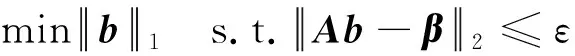
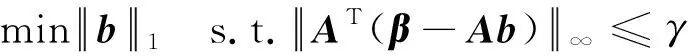

3 復雜度分析

4 實驗仿真分析

4.1 測量矩陣性能分析
4.2 算法有效性分析

4.3 分辨率分析

4.4 算法性能對比


5 結 論

