基于RST-NMF模型的微震信號時頻分析和識別

張法全， 王海飛， 王國富， 葉金才

(1.桂林電子科技大學 信息與通信學院，桂林 541004；2.廣西無線寬帶和信號處理重點實驗室，桂林 541004)

近年來，微震監測技術憑借其有效的地壓監測手段被廣泛的應用于煤礦安全高效生產領域[1]。微震信號識別是微震監測技術的主要部分,微震信號屬于典型的非線性、低信噪比信號[2-3]，其包含了巖石破裂信號、煤礦爆破信號、機械震動和其他施工噪聲信號[4]。如何精確的識別微震信號是微震監測技術的關鍵問題。

目前，針對微震信號的處理主要采用傅里葉變換(Fourier Transform, FT)、小波變換(Wavelet Transform, WT)、S變換(S-Transform, ST)等時頻分析方法[5]。江文武等[6]采用FT對大震級微震信號的頻譜進行分析。Ma等[7-8]在FT的基礎上進行小波切片和重構，彌補了FT的不足，唐守峰等[9]通過WT提取微震信號特征，為微震信號的模式識別打下了重要基礎，朱權潔等[10]采用小波包與分形維結合提取信號特征，對微震信號做了初步識別，但是小波分析結果與基函數的選擇緊密相關[11]。ST集成了短時傅里葉變換(Short-time Fourier Transform, STFT)和WT的優點，姜鵬等[12]將ST引入微震波信號識別領域，提取ST的能量分布特征進行分類，取得了較好的效果，但是該變換受到測不準原理的制約，其時頻分辨能力有限。

非負矩陣分解(Nonnegative Matrix Factor, NMF)是一種新型的特征提取方法，可以得到原始數據的低秩矩陣[13]。傳統的特征提取方法需要假設測量數據服從一定的分布[14-15]，如主成分分析(Principal Component Analysis, PCA)需要測量數據服從于高斯分布，獨立成分分析(Independent Component Correlation Algorithm， ICA)能對非高斯數據進行有效處理，卻對高斯數據的處理效果較差，而NMF算法對測量數據的性質僅有非負性的要求，能夠有效處理高斯及非高斯分布的數據，且NMF分解得到的低維矩陣具有非負性和稀疏性，能夠有效提取數據的局部特征和內在聯系[16-17]，并在一定程度上抑制外界環境的干擾。

時頻重排可以有效的聚集時頻能量，提高時頻分辨率[18]。本文將ST和時頻重排相結合提出RST(Rearranged S Transform, RST)，以期達到在增強微震弱振幅信號的頻域分量的同時又能提高時頻分辨率。借用NMF技術分解時頻矩陣，提取其分解量的宏觀、微觀統計量信息以期構造完備的特征空間，以期避免過擬合的發生。

1 RST-NMF理論

1.1 RST

由于ST對信號開窗分析，受到海森堡效應的制約，導致其時域分辨率和頻域分辨率有限。本文將重排技術與ST相融合，在一定程度上聚集時頻能量，提高時頻分辨率，過程如下。

對于任意一個時變信號x(t)的S變換表達式如下

(1)

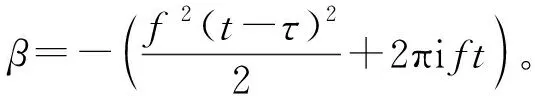
通過把某點(t,f)處的輸出作為該點臨近區域內能量分布重心處的輸出，達到頻譜在抑制交叉項的同時又提高了時頻聚集性。

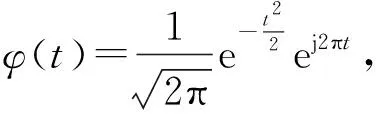
(2)

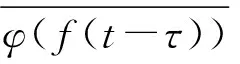
由帕塞瓦爾定理[19]和傅里葉變換的性質可將式(2)變換為式(3)

(3)

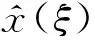
由此得到重排變換的算子如式(4)和式(5)

(4)

(5)

因此經過重排后的ST的表達式如下

(6)

1.2 NMF

NMF定義如下

(7)

式中，VN×M為待分解的N×M維非負矩陣，WN×r為分解基向量矩陣，Hr×M為分解系數矩陣。

NMF的實現過程實際上可理解為一個帶約束的非線性的優化求解問題，本文基于歐幾里得距離度量[20]，建立如下目標函數

(8)

通過迭代式(7)和式(8)可求解出WN×r、Hr×M

(9)

(10)

式中，WN×r反映了信號的頻域特征，Hr×M反映了信號的時域位置特征。

2 算例分析

下面通過三道溝井田微震監測項目，測試RST-NMF算法在信號時頻分析和特征提取的性能。

三道溝的地質特征屬于典型的黃土丘陵溝壑地貌。淺層地質廣泛分布第四系淺黃色黏土、亞黏土、粉沙、細沙層，底層偏松軟；深層地巖主要為砂泥巖夾煤層，沉積較穩定，地層平緩，煤層埋藏淺。

根據實際地形情況，最終布置了12個傳感器，使用圓形布陣如圖1所示。

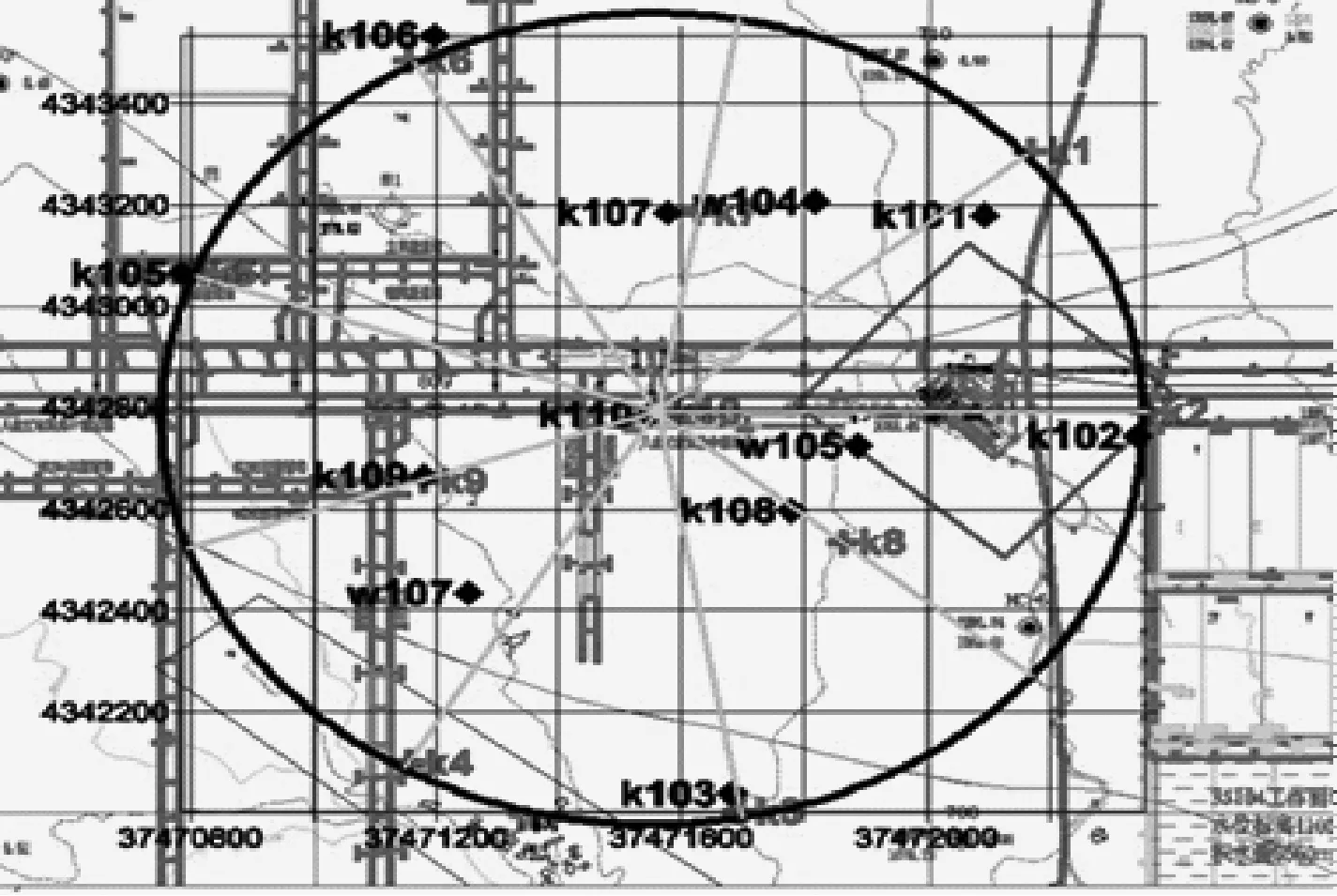
圖1 基站檢波器圓形布局圖

2.1 基于RST的微震信號時頻分析

從采集的微震信號中選取巖石破裂信號(圖2(a))、爆破震動信號(圖2(b))以及機械噪聲信號(圖2(c))為樣本進行分析，其波形如圖2所示。

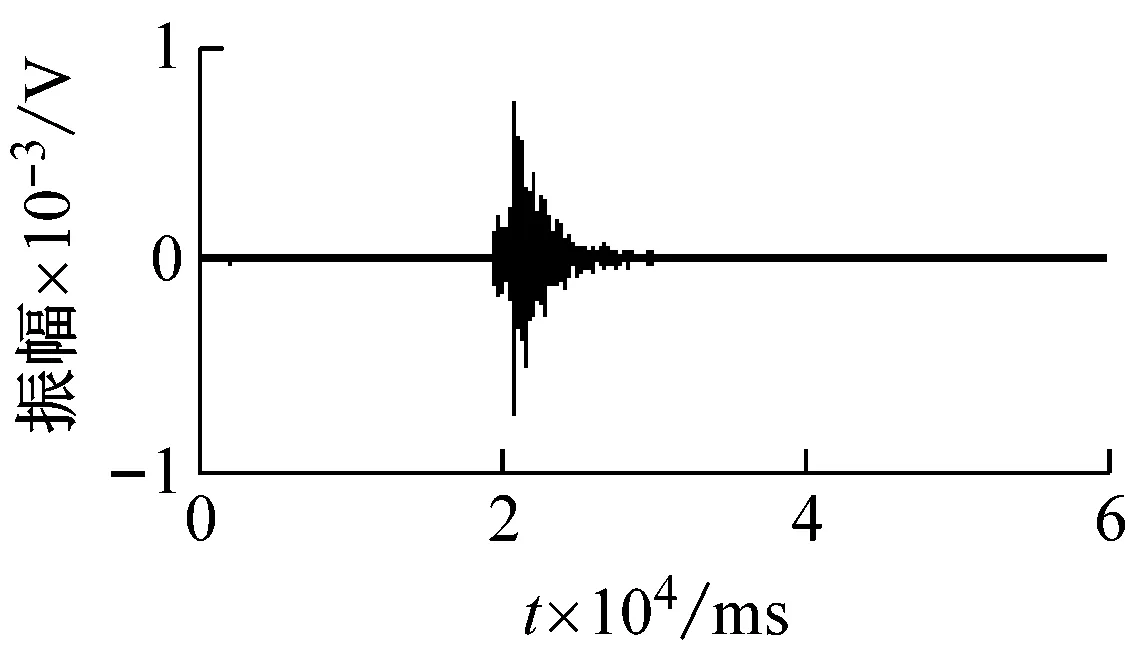
(a) 巖石破裂信號

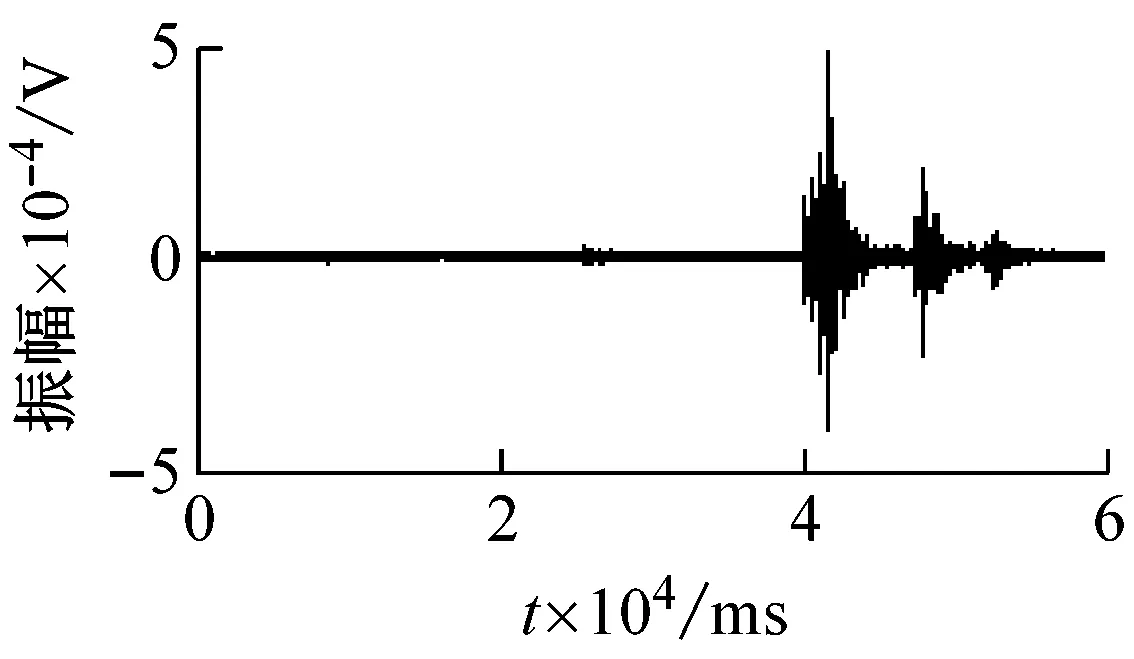
(b) 爆破信號

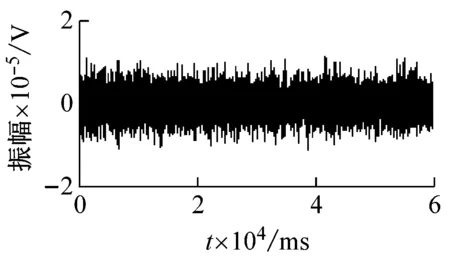
(c) 機械噪聲信號

圖2 信號波形

Fig.2 Waveforms of signals

由圖2可知,震源不同，微震信號波形也不同。巖石破裂信號的振幅相對較大，是由于巖石受高應力發生形變和破斷時，釋放出大量彈性勢能，且持續時間短。而爆破信號高頻成分的吸收衰減相對嚴重，低頻成分相對突出，一般伴隨2～3個地震子波。機械噪聲是由環境中的噪聲生成的，因此持續時間較長，并且震幅較小且平穩。

對上述微震信號進行時頻轉換。為了顯示RST變換的聚集性，這里同時進行ST對比。得到相應的時頻圖，如圖3所示。

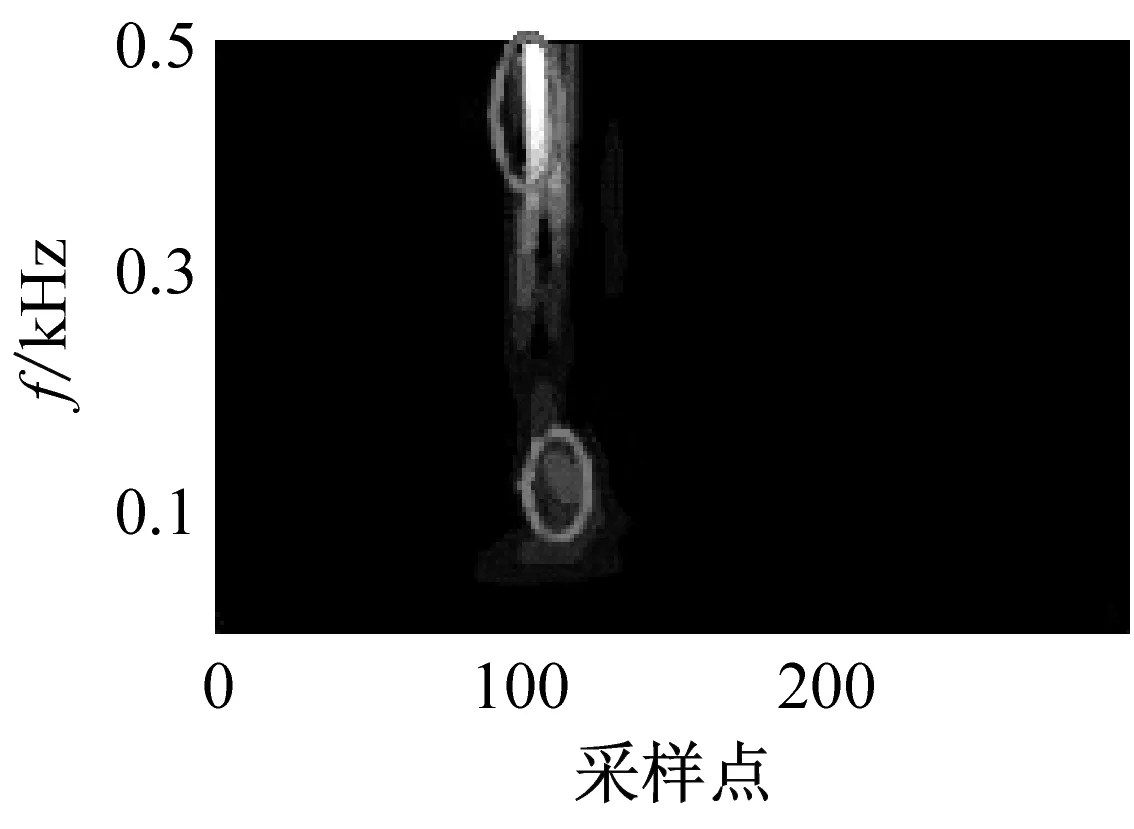
(a) 巖石破裂信號的ST譜

(b) 巖石破裂信號的RST譜

(c) 爆破信號的ST譜

(d) 爆破信號的RST譜

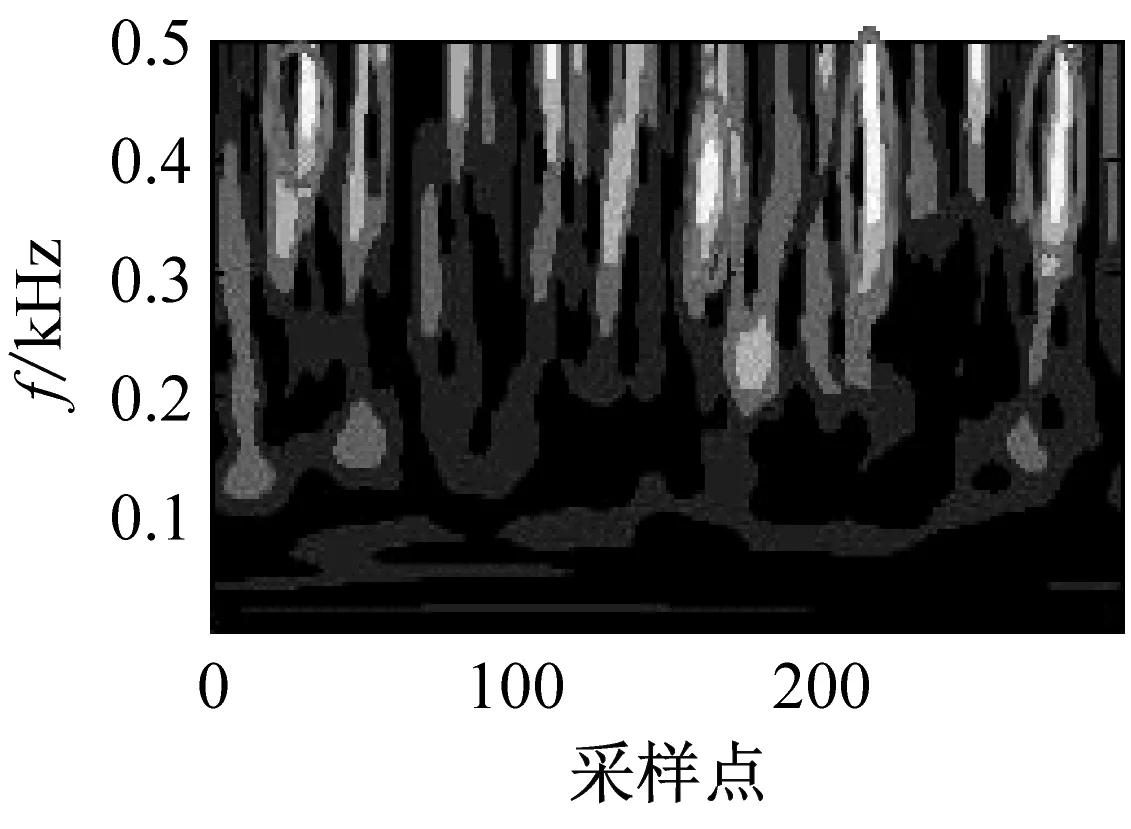
(e) 機械噪聲的ST譜

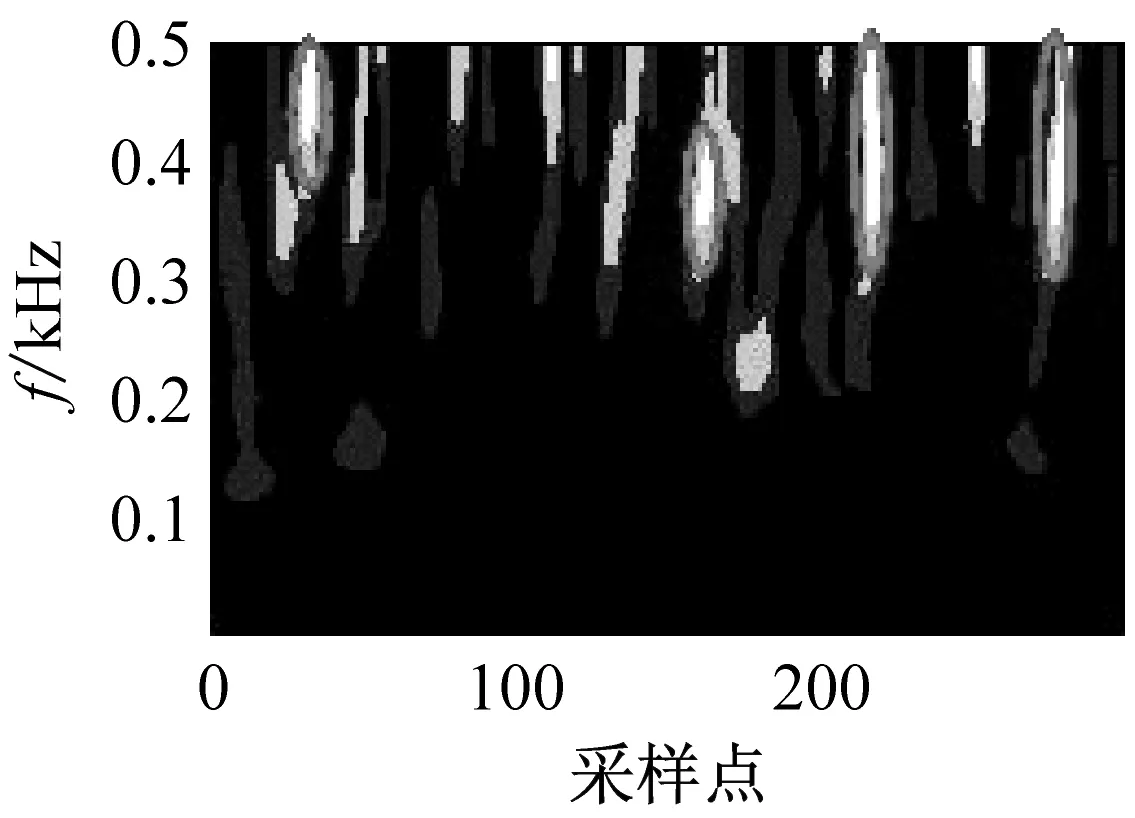
(f) 機械噪聲的RST譜

圖3 信號ST和RST

Fig.3 Signal time spectrum of ST, RST

在圖3中，橢圓部分為微震信號時頻能量的主要分布區域，可以看出RST的時頻分辨率明顯高于的ST時頻分辨率。從整體上巖石破裂信號的時頻譜比較單一，能量主要分布在[400,500]Hz高頻區域，信號持續時間較短，大約30 ms。爆破信號的時頻譜擁有明顯的兩個能量團，集中分布在[200,300]Hz之間，持續時間大約100 ms。機械噪聲的時頻譜比較豐富，分布于整個頻帶上并持續發生。

2.2 重排時頻矩陣的NMF分解

利用NMF分解技術對微震信號的RST矩陣分解，得到相對應的分解基向量W和系數向量H，其分布特征如圖4所示。

在圖4中，1表示巖石破裂信號，2表示爆破信號，3表示機械噪聲，w表示頻域基向量，h表示時域位置向量。

由圖4可知，巖石破裂信號持續時間較短，在50 ms左右，振幅較大，最大達到了20 mV，爆破信號的持續時間較長，大約有100 ms，振幅相對于巖石破裂信號較小，最大為7 mV，而機械噪聲的持續時間較長，分布于整個時間軸上，但是其振幅較小且均勻，大約在2 mV。而系數矩陣的分布，并沒有呈現明顯的規律性。

2.3 提取特征

標準差用來反映一組數據的波動程度，其定義如下

(11)

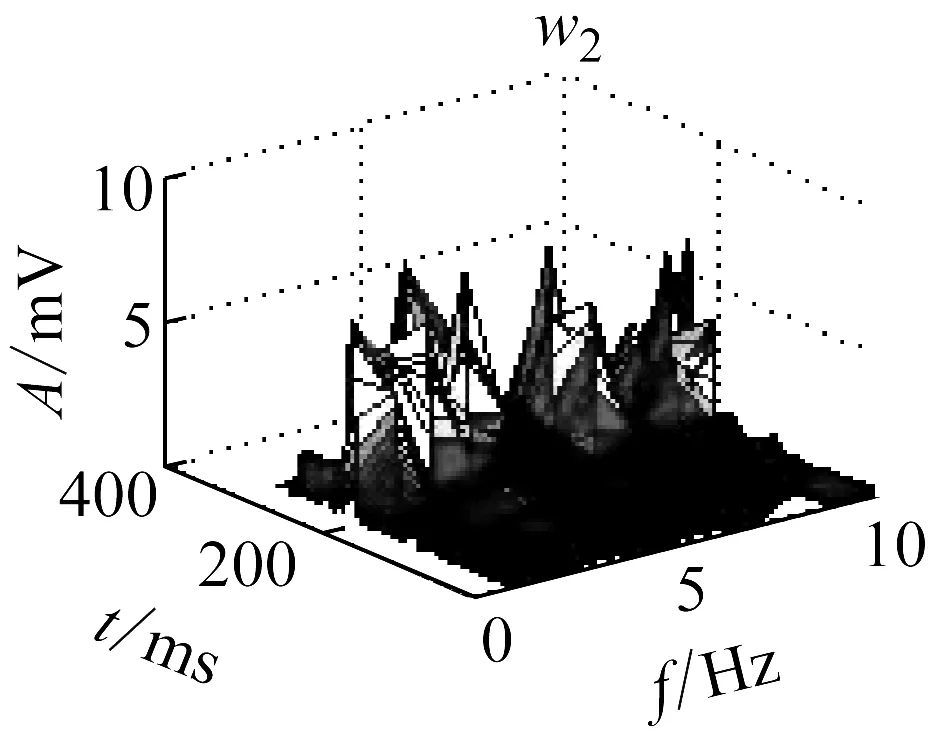
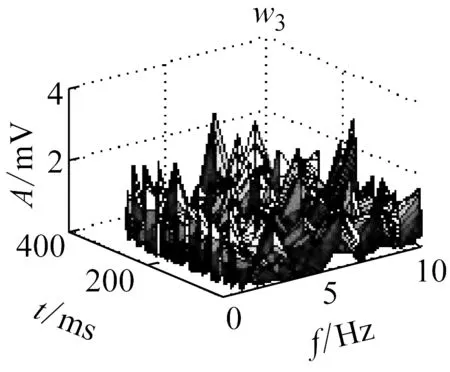
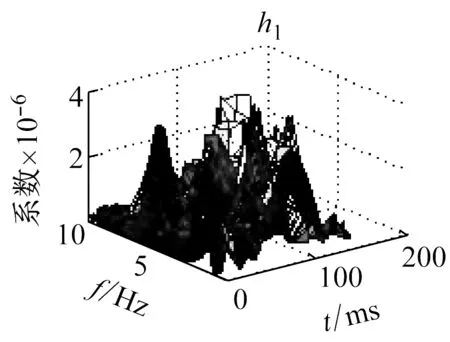
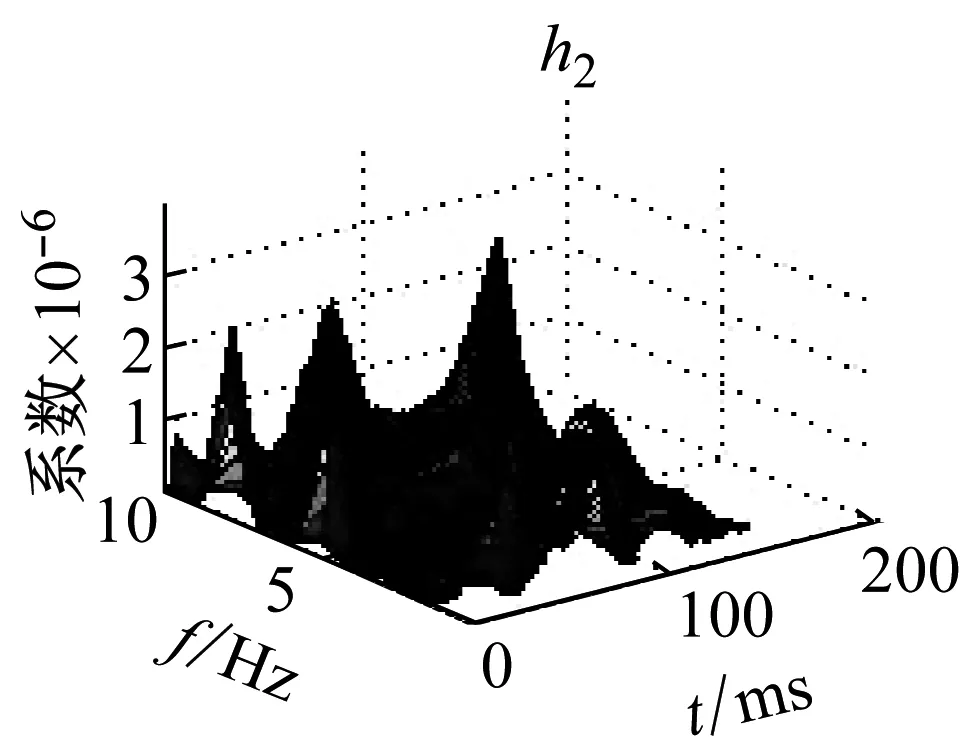
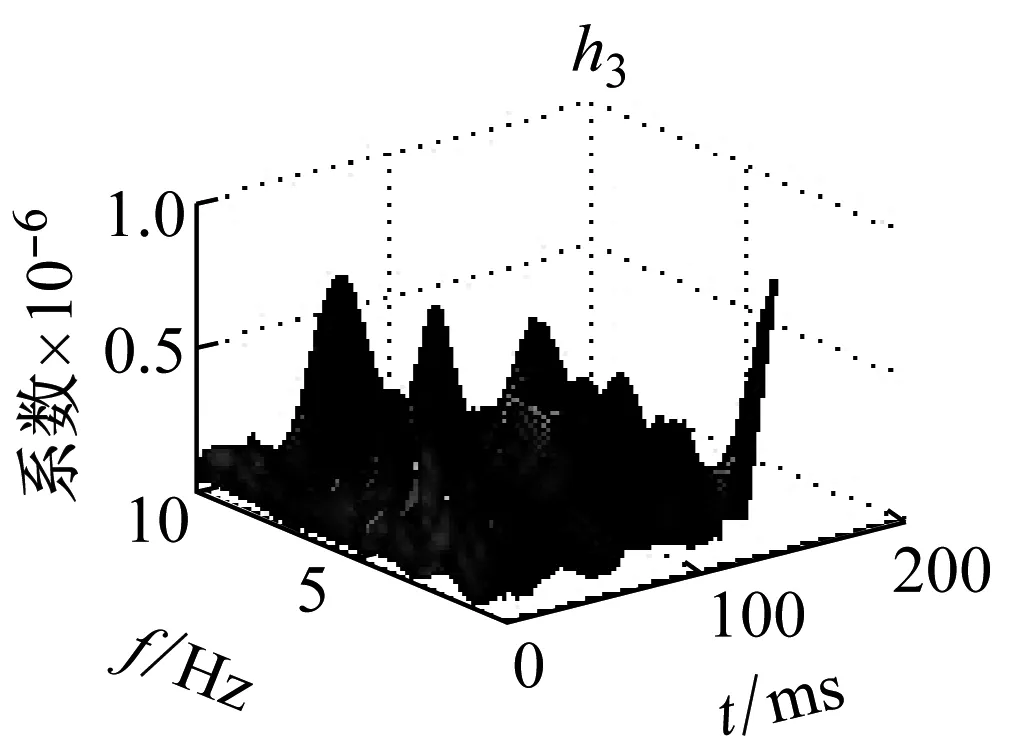
圖4 分解向量分布圖

Fig.4 Decomposition vector distribution

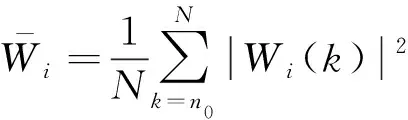
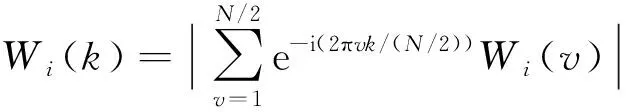
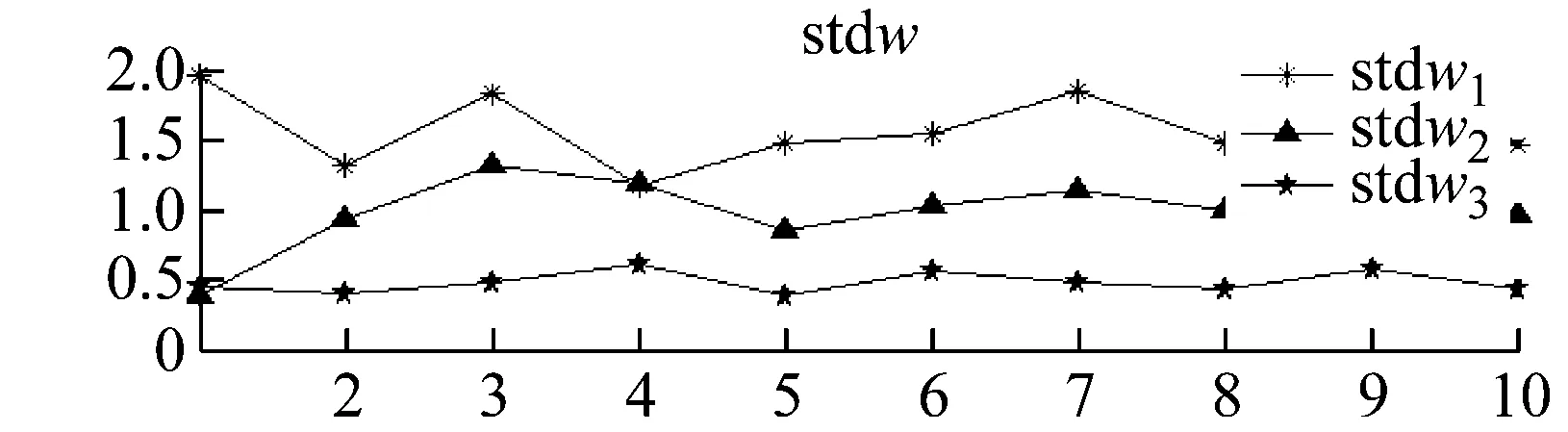
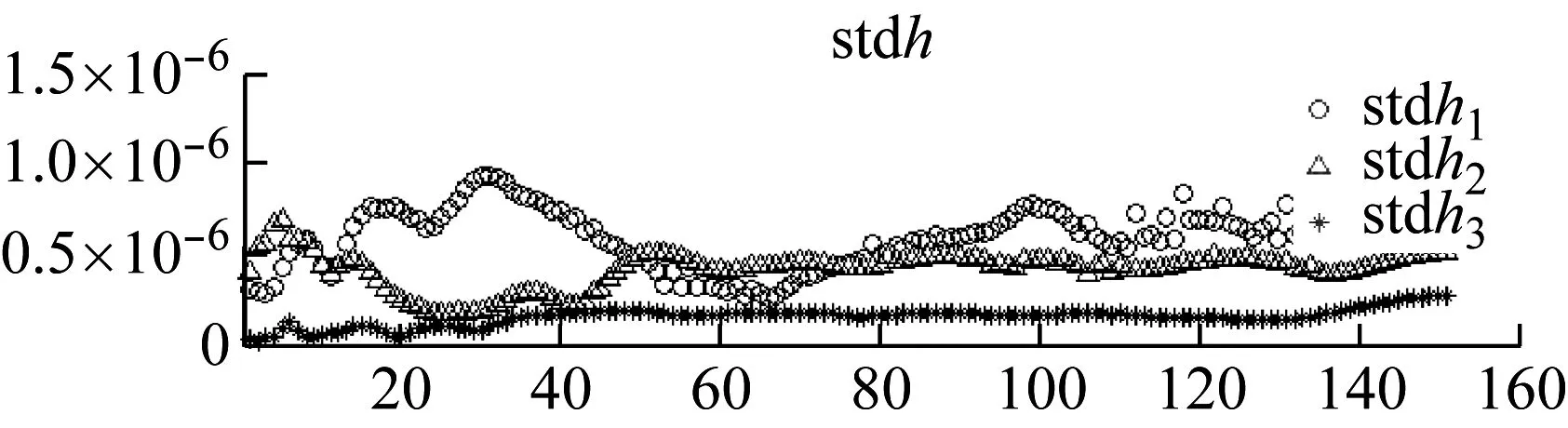
圖5 標準差

由圖5我們可以明顯看到,巖石破裂信號的頻域基向量的波動程度在整體上大于爆破信號的波動程度，爆破信號的波動程度又明顯大于機械噪聲的波動程度。巖石破裂信號和爆破信號存在明顯的極值點，極小值分別為0.75 mV2/s，0.25 mV2/s，極大值點分別為2 mV2/s，1.1 mV2/s。巖石破裂信號時域位置向量的標準差和爆破信號的波動程度相當，但都大于機械噪聲的波動程度，機械噪聲的波動值較小接近于0，說明機械噪聲的時域位置向量基本平穩。

WN×r的相關系數反映一組數據中相鄰元素之間的相關性

(12)

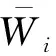
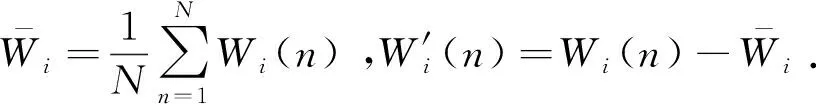
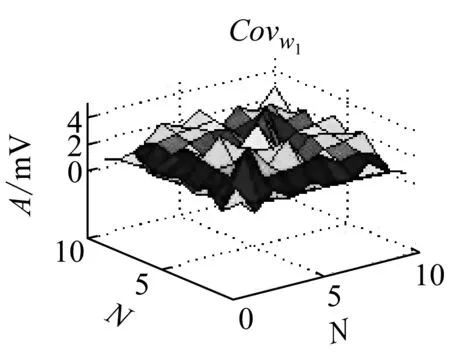
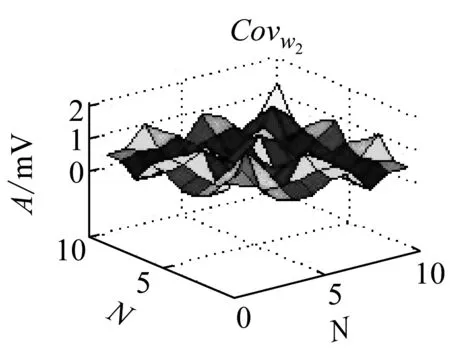
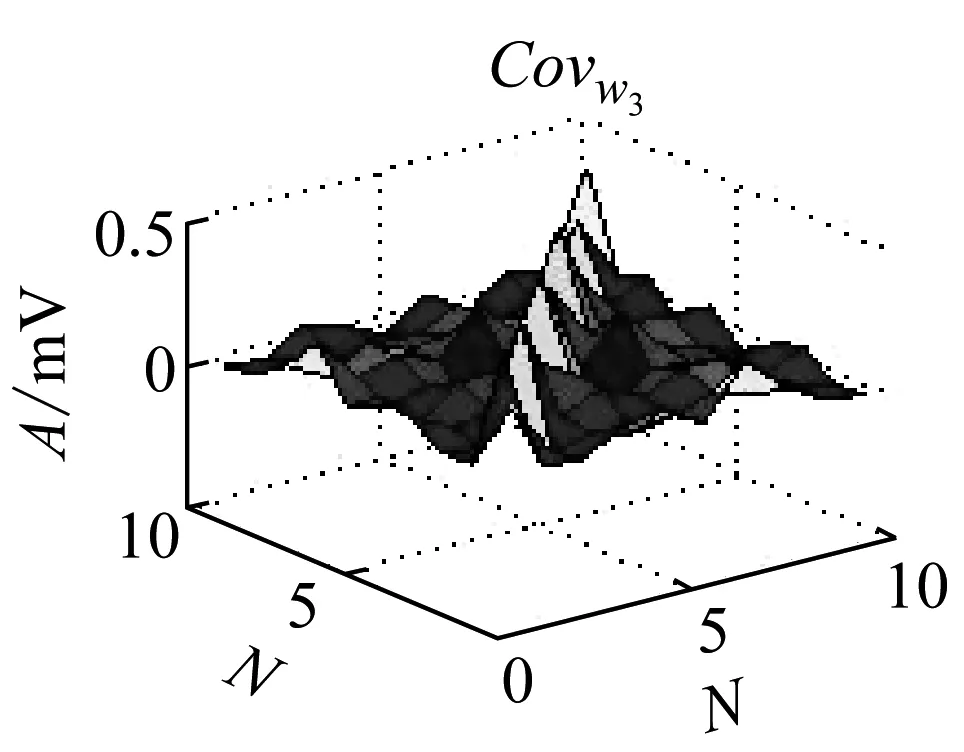
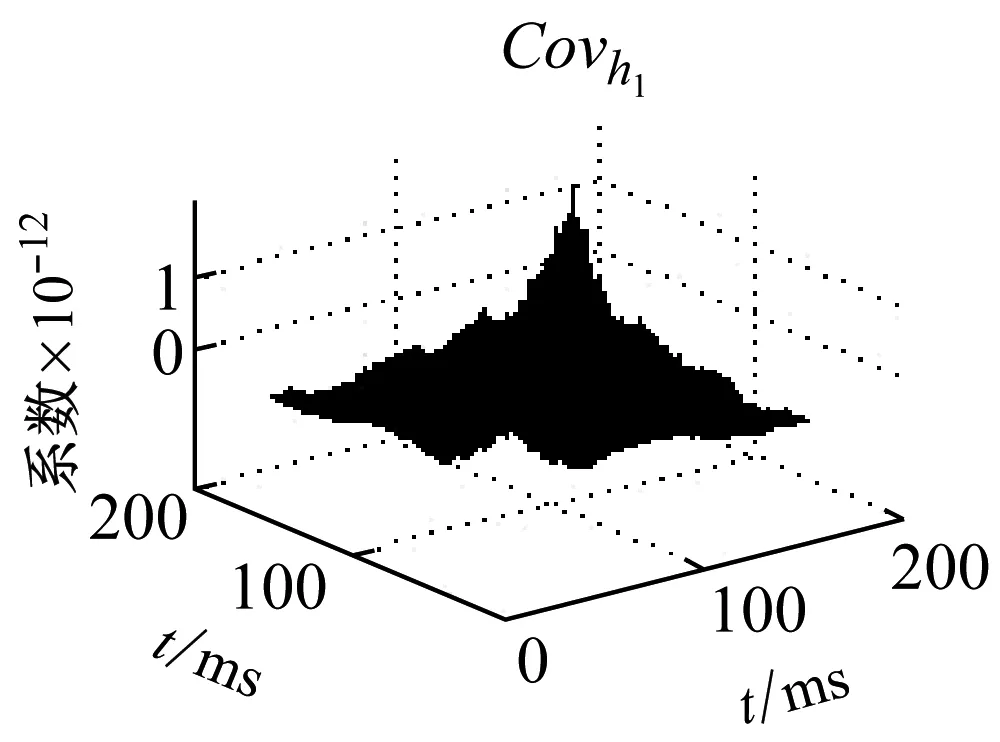
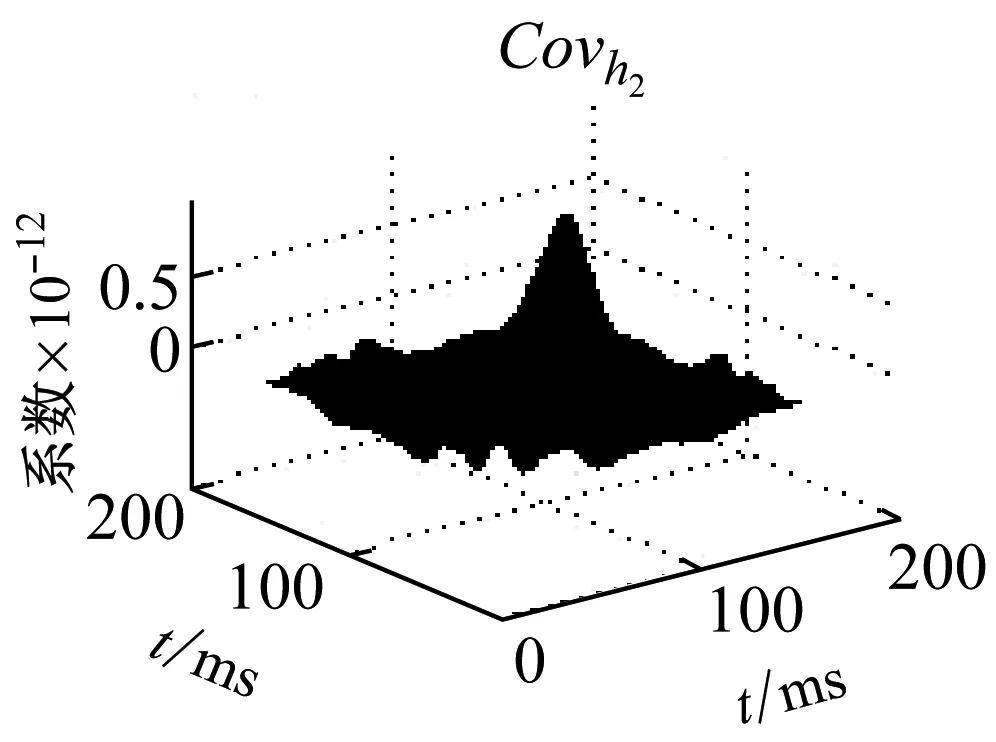
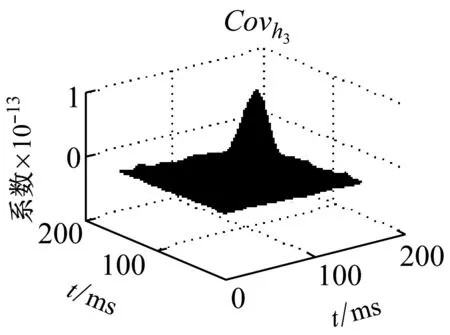
圖6 相關系數

Fig.6 Coefficient of association

在圖6可知，可以看出巖石破裂信號的相關性分布較均勻且基本大于1，說明巖石破裂信號的相鄰時刻元素之間的變換存在較強的相互關系，相關系數在[1,3]之間,爆破信號的相關系數集中在[-0.5,1.5]之間，機械噪聲的相關系數在[0,0.3]之間，相關性較小。

導數反映一組數據的變化趨勢

(13)

其分布如圖7所示。

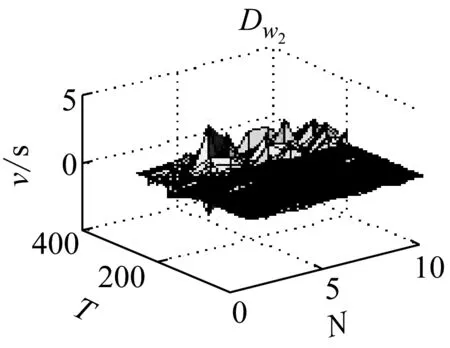
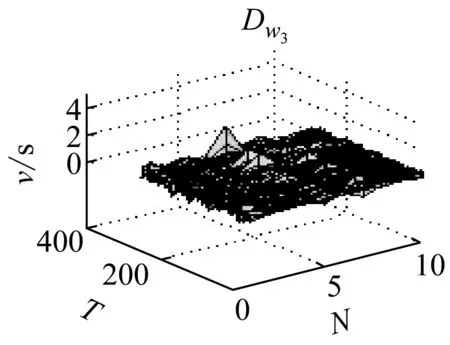
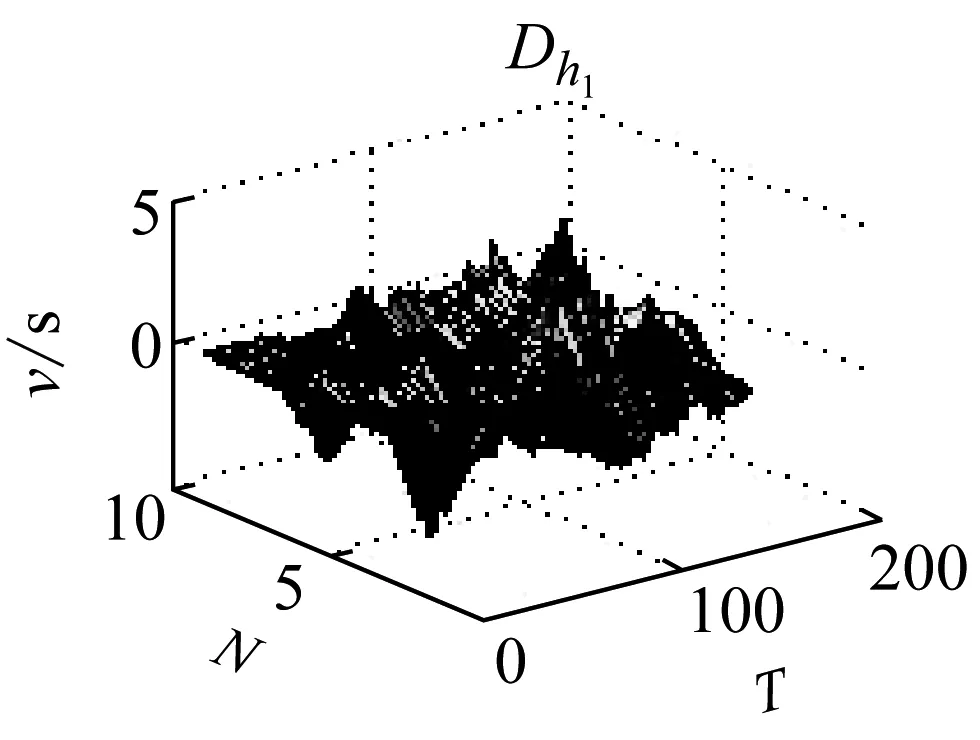
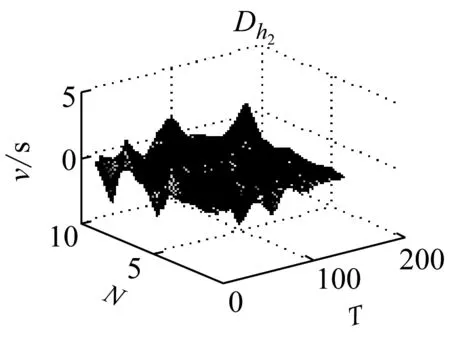
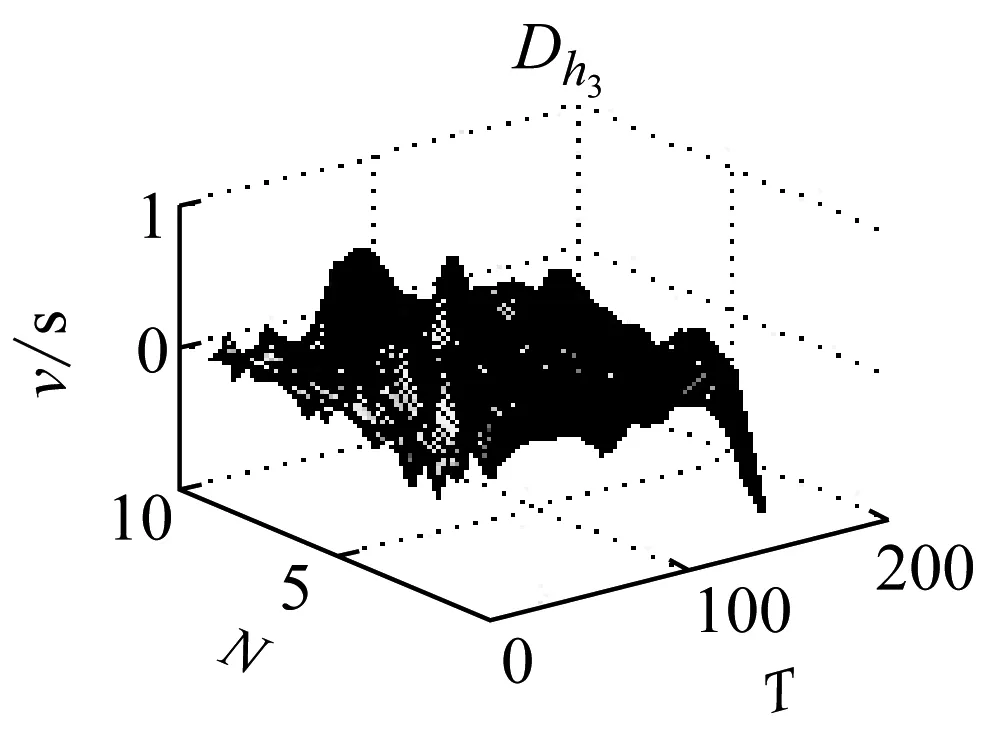
圖7 導數

Fig.7 Derivative

由圖7可以很明顯看出,Dw1在巖石破裂信號的發生的區域導數的變換比較急劇，這是由于巖石破裂信號是受剪切型應力作用的結果，Dw2導數分布呈現緩慢變換的趨勢，這是由于爆破信號發生的受介質傳播的影響，持續時間長，且產生子波。而機械噪聲的導數基本穩定在零附近，說明機械噪聲比較穩定。

稀疏度：

(14)

式中，M為hi的長度。

綜上所述，從每個頻域基向量Wi中提取標準差SDwi、協方差Covwi、導數Dwi三個特征向量，從每個時域位置向量Hi中提取標準差SDhi、稀疏度SPhi兩個特征向量。構造特征空間如下

F=(SDwi,Covwi,Dwi,SDhi,SPhi,…)

(15)

式中,下標wi說明為第i個頻域基向量的特征，其中i=1,2…N。

2.4 震信號多類分類SVM模型

為了將該算法具有更廣闊的工程應用，本文采用支持向量機(Support Vector Machine, SVM)把微震信號分為巖石破裂信號、爆破信號和機械噪聲信號三類，對應的分類標簽為1、2、3。圖8為本文的分類器模型。

由圖8可知，針對微震信號的分類步驟如下：

步驟1 對已知微震信號進行重排ST；

步驟2 對步驟1得到的結果進行NMF分解；

此次網格化管理試點在原來基礎上加以改進，以前社區網格化成員是由社區里面的工作人員下網格，他們既要完成自身的工作還要承擔網格里的工作，導致分身乏術，兩邊工作都無法兼顧。 本次網格化管理是區里面統一從社會上招聘專門的人員，分配到各個社區，工作歸各個社區管理，檔案工資等人事方面歸街道管理。 剛開始試點兩個月多月，書記表示如果此次網格化試點運行順暢，確實能夠幫社區減清一些負擔。

步驟3 步驟2中得到的結果提取標準差、導數、稀疏度、相關系數等信息統計量構造特征空間；

步驟4 采用自助法[21]選擇訓練樣本和測試

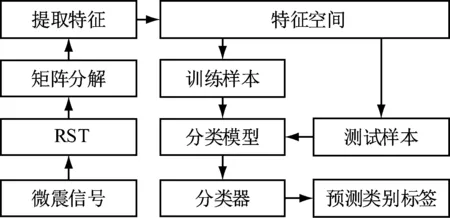
圖8 分類器模型

樣本；

步驟5 訓練模型得出分類標簽。

2.5 不同時頻變換方法的識別結果

下文在分類識別中均采用SVM分類器，Gauss核函數，懲罰參數C=2，Gauss核寬度γ=1。分類結果的優劣，沿用文獻[5,8]中以

準確率=識別正確總數/樣本總數為標準。

為了測試RST變換的優越性，本文選取ST的時頻分析方法對比，分類結果如表1所示。

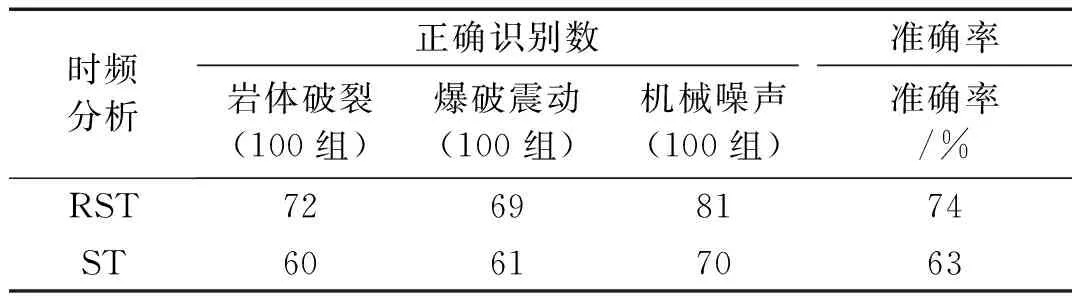
表1 不同時頻變換方法的分類結果

2.6 不同分解方法的識別結果

為了證明RST-NMF的優越性，本文分別采用局部特征尺度分解法 (Local Characteristic-scale Decomposition, LCD)[22]、局部均值分解法(Local Mean Decomposition, LMD)[23]方法對比，分類結果如表2所示。

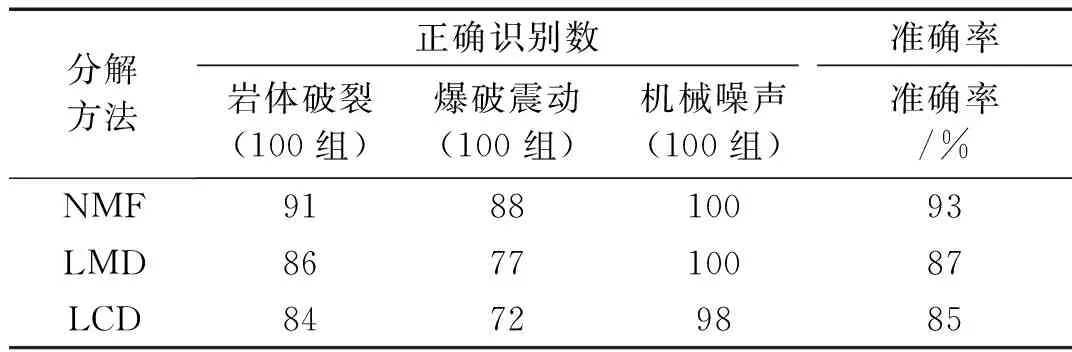
表2 不同分解方法的分類結果

由表2可知,RST-NMF方法的準確率高于LMD、LCD，這是由于LCD、LMD的自適應分解存在端點效應、模態混疊等問題，降低了信號的保真度，導致在分類時存在過擬合的問題，總體來說RST-NMF識別效果較優。

2.7 不同特征空間的識別結果

為了證明特征空間F的優越性，本文選取常用的特征空間相關系數Cov、能量譜系數ECov對比，結果如表3所示。

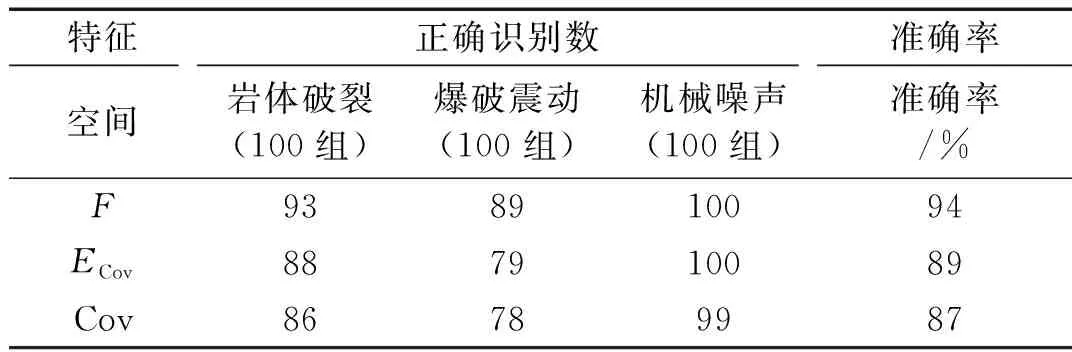
表3 不同特征空間的分類結果

由表3可知：特征空間F的識別正確率大于Cov、ECov識別正確率，即F包含了更多微震信號的特征信息。

3 結 論

本文針對微震弱振幅信號難以識別的問題，提出了RST-NMF的時頻分析和特征提取算法得出如下結論：

(1) RST時頻分析方法，對頻域分散的能量團有很好的聚集性，增強微震弱振幅信號的時頻分辨率。

(2) 時頻矩陣經NMF分解最大程度上獲取微震信號的局部特征和內在聯系，并在一定程度上抑制外界環境的干擾。

(3) 提取NMF分解向量的宏觀和微觀統計量標準差、導數、稀疏度、相關系數，保證了提取的信號特征空間集完備性，可以有效避免分類時欠擬合的發生。