高中數學實驗初探

吳超嫦

摘 要：數學既是一門演繹科學，又是一門實驗歸納科學。在數學教育中，數學實驗的實施有助于學生對數學理論的直觀認知，數學實驗是結合數學教育需要，適應教育技術發展的重要手段。數學實驗的類型包括驗證性數學實驗和探索性數學實驗，驗證性數學實驗立足已知的結論，通過實驗形式展現推導過程，給予學生理論描述更直觀的體會;探索性的數學實驗則通過對未知結論的探索，引領學生進行數學思維的構建。數學實驗是數學理論的再發現的途徑之一，可豐富教學形式，推動數學教育的發展。

關鍵詞：數學教育;數學實驗;探索性數學實驗;驗證性數學實驗;教育發展

一、什么是數學實驗

在數學領域，對數學實驗有著不同的理解和看法。本文中的數學實驗并非簡單地指“思維實驗”，而是指在一定的實驗條件下，借助一定的物質手段，借助數學思維活動，為獲得一定的數學理論和檢驗一定的數學思想而進行的探索和研究活動。從實驗的目的來看，數學實驗可以分為驗證性實驗和探索性實驗。

二、為什么要在高中數學教學中開展數學實驗

1.數學自身特點決定了要在教學中開展數學實驗

美籍匈牙利數學家、數學教育家喬治·波利亞（George Polya）曾精辟地指出：“數學有兩個側面，一方面它是歐幾里得式的嚴謹科學，從這個角度看，數學像是一門系統的演繹科學;但另一方面，創造過程中的數學，看起來卻像一門實驗性的歸納科學。”根據瑞士數學家歐拉的說法，“數學是一門需要觀察和實驗的科學。因此，數學不僅是一門演繹和推理的學科，也是一門實驗和歸納的學科。

2.學生的認知特點決定了要在教學中開展數學實驗

夸美紐斯，16世紀著名的捷克教育理論家和實踐者，在《大教學論》中提到過：“知識的開端永遠是從感官來的”“科學的真實性與可靠性，其所依賴于感官的證明比其他一切事項要多。”“感官是記憶最可信的仆役，所以，如果這種感官的自覺方法能被普遍采用，它就能使知識一經獲得以后，永遠保住。”

皮亞杰的認知發展理論認為：認知發展過程是主體的主動建構過程，主體對信息進行整理、歸類、創造，并將之納入已有的認知結構中。因此，知識不是由教師傳授的，而是由學習者在一定的社會和文化背景下，在其他人（包括教師和學習伙伴）的幫助下，借助必要的學習材料和通過意義的建構來獲得的。

美國教育家戴爾的“經驗之塔”理論把學習分為三類，共十個層次，從下到上是寶塔形的，分別是做的經驗、觀察的經驗和抽象的經驗。戴爾認為，教育應該從具體的經驗開始，逐步抽象。數學學習的有效途徑應該是充滿具體的數學經驗的，而獲得數學經驗的最佳途徑就是做數學實驗。

3.數學教育的需求決定了要在教學中開展數學實驗

在數學教育中，邏輯推理一直受到人們的重視，而實驗、猜測、歸納、創新能力的培養，對科學突破具有重要意義，卻沒有得到足夠的重視。學生越來越不了解數學從何而來，感覺越來越枯燥，越來越不喜歡數學。

數學教育專家鄭毓信教授認為，在數學教育中，我們不應該唯一強調數學知識的掌握，而應更加重視，使學生像數學家一樣去工作，像數學家一樣去思維。而在數學教學中進行數學實驗，可以使學生在教師的指導下，從“聽”轉變為“做”。從過去被動地接受現成的數學知識，轉變為現在像“研究者”一樣去發現和探索知識。中科院院士、數學教育學家姜伯駒指出，“應該組織數學實驗課程，在教師指導下，通過學生自己動手計算、體驗解決問題的過程，探索某些理論或應用的課題，使新鮮想法借助數學軟件可以迅速實現，從而在失敗與成功中得到真知。這種方式，變被動的灌輸為主動的參與，有利于培養學生的獨立工作能力和創新精神。”

4.教育技術發展的狀況決定了可以在教學中開展數學實驗

近年來，多種多樣的實物模型變得非常常見，計算機、TI圖形計算器也逐漸在學校里普及，這為數學實驗的開展提供了物質保障，《幾何畫板》《數學實驗室》《Z+Z智能教育平臺》《Mathmatica》《Maple》《MATLAB》《MathCAD》等一批軟件的應用則提供了強大的技術支持。現在，我們不僅能使用模型等實驗手段進行傳統的“數學實驗”，也能利用各種軟件進行廣泛的計算機輔助實驗。

三、怎樣開展數學實驗

1.數學實驗設計的基本原則

數學實驗設計除了遵循教學設計的一般性原則以外，還應注意以下幾點：

（1）實驗內容應當適合學生的知識水平和年齡特點。

（2）實驗問題要貼近學生生活，以激發學生研究興趣，讓學生從實驗過程中了解數學的價值。

（3）實驗過程應可控、可伸縮，可隨時添加一些數學元素或條件，以幫助探索問題。

（4）實驗通常由學生直接進行，通過啟發式提問，教師在學生實驗過程中起到引導、輔導和幫助學生學習的作用。

（5）要設計實驗報告，學生在實驗后完成。

2.驗證性實驗教學案例

驗證性實驗是通過實驗操作和觀察，記錄和分析來測試數學判斷或結論的真實性的實驗。作為一種常見的理解方式，這種數學實驗是演繹與歸納相結合的。通常教師演繹新的結論時，由于抽象的結論和復雜的推理過程，學生在心理上較難接受，而通過實驗，學生親身經歷了知識產生、形成的過程，使新知識具體化，更好地提高了學生對新知識的認識和理解。

案例1：

【實驗課題】同時擲兩枚質地均勻的硬幣時各事件發生的概率。

【實驗內容】同時擲兩枚質地均勻的硬幣50次，統計“一枚正面朝上一枚反面朝上”“兩枚正面朝上”“兩枚反面朝上”三種結果發生的次數，驗證這三個事件的概率分別為1/2、1/4、1/4，并根據實驗數據分析其原因。

【實驗目標】糾正學生的錯誤觀點：“一枚正面朝上一枚反面朝上”“兩枚正面朝上”“兩枚反面朝上”三個事件是等可能事件。引導學生正確分析試驗中的基本事件。

【實驗準備】兩枚質地均勻的一元硬幣，兩人合作，一人擲硬幣，另一人記錄。

【實驗過程】

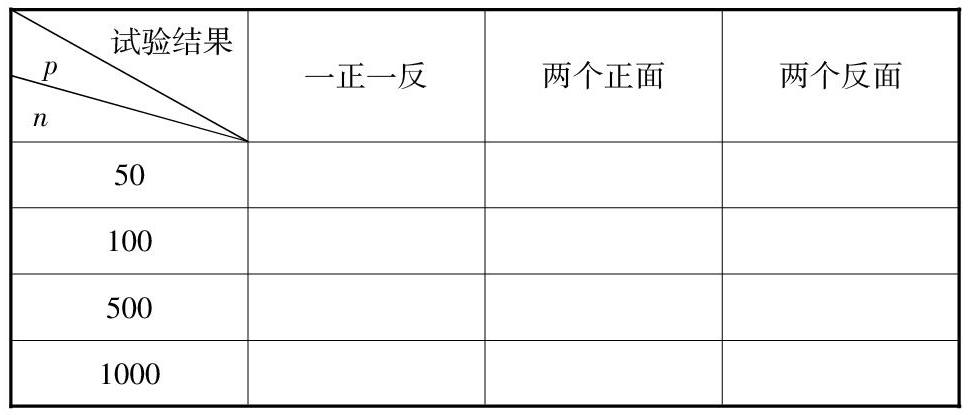
（1）一人同時擲兩枚質地均勻的硬幣50次，另一人記錄“一枚正面朝上一枚反面朝上”“兩枚正面朝上”“兩枚反面朝上”三種結果發生的次數。

（2）填表。

表1：擲硬幣試驗次數n=50。

表2：匯總其他小組的試驗結果后填寫下表。其中擲硬幣試驗次數為n，事件發生頻率為P。

（3）根據實驗結果，我們可以估計同時擲兩枚質地均勻的硬幣，出現“一枚正面朝上一枚反面朝上”的概率為____________，出現“兩枚正面朝上”的概率為____________，出現“兩枚反面朝上”的概率為____________。

（4）試著根據這三個事件的概率大小，分析其原因。

【延伸實驗】

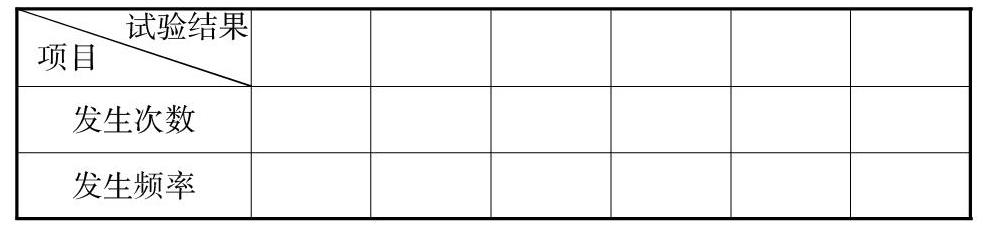
將兩枚質地均勻的硬幣分別標上記號“A”“B”，再同時拋擲50次，會出現哪些試驗結果？記錄并填寫下表：

根據實驗數據，我們可以估計同時擲兩枚質地均勻的硬幣，以上結果發生的概率各是多少？這個概率與前面的實驗中所得的概率有什么聯系？

此案例的實驗簡單易操作，一方面讓學生體驗了通過實驗得出頻率，再用頻率估計概率的研究方法，另一方面用數據糾正了“擲兩枚硬幣出現‘一正一反的概率為1/3”的錯誤認識。通過對知識結論的驗證，無論是積極的還是消極的，都可以培養學生的科學精神，而且可以鞏固學生所學的知識。

3.探索性實驗教學案例

探究性實驗是通過實驗探索，回答學生不知道答案的數學問題，一般也不提供實驗材料，只提供實驗課題。事實上，它為學生通過探究學習數學知識提供了一種實用的途徑，強調探究過程中數學知識的獲取和數學理解。

案例2：

【實驗課題】利用幾何畫板探索指數函數的性質。

【實驗內容】形如y=ax（a>0且a≠1）的函數叫作指數函數，本實驗擬用幾何畫板作為工具探索指數函數值域、單調性、奇偶性以及底數a對函數圖象形狀的影響等方面的性質。

【實驗目標】探索利用動點研究函數性質，獲得指數函數相關性質的方法，培養學生觀察、分析、抽象、概括等數學思維能力的實踐能力，并培養學生運用計算機技術理解數學和解決數學問題的能力。

【實驗準備】為每臺計算機安裝幾何畫板;要求學生復習幾何畫板的相關用途，如根據坐標構點、繪制函數圖象等;一組四人，每組一臺計算機。

【實驗過程】

（1）從圖象探索指數函數的基本性質。

打開幾何畫板新建頁面1，新建參數a（設置參數鍵盤調節單位為0.2，下同），初始值a=0.1，繪制新函數y=ax;觀察圖象有什么特征？

觀察與思考：

①函數圖象分布在第幾象限？這說明函數中x和y的取值范圍是什么？

②函數圖象從左往右看是上升還是下降？說明指數函數的什么性質？

③函數圖象的對稱性如何？反映了指數函數的什么性質？

（2）探索底數a對函數圖象形狀的影響。

改變參數a的值，觀察指數函數圖象的變化，可以發現什么規律？

（3）研究指數函數y=ax和y=（1/a）x圖象的關系。

①繪制函數y=ax和y=（1/a）x的圖象，猜想________________________。

②選定函數y=ax圖象，構造圖象上的動點P，作出P關于的對稱點P'，觀察P'的位置與函數圖象y=（1/a）x有什么關系？

③結論：________________________________________________。

在上面的案例中，教師提出問題，在教師的指導下，學生在規定的時間內按照預先安排的組織進行實驗材料的操作和實驗。根據實驗現象的觀察或數據記錄以及數據分析和處理的結果，進行初步的猜測，并考慮其原因。然后各個小組進行討論和交流，最終獲得大家都認可的結論。在這個過程中，學生自己動手，通過實驗來探索和發現各種規律。這不僅使新知識找到了堅實的附著點，而且使學生的數學認知結構在探索過程中得到了發展。

數學實驗是再現數學發現過程的有效途徑。它豐富了數學學習的形式，為學生提供了一個主體參與、積極探索、大膽實踐和創新的學習環境，為解決數學問題提供了新的途徑。在高中數學教學中開展數學實驗是現代教學方式發展的需要，這是改變教學方法的有益嘗試，它將促進教育技術的發展，并將創造、豐富和發展創新教育理論。

參考文獻：

[1]讓·皮亞杰.皮亞杰學說及其發展[M].湖南教育出版社，1983.

[2]埃德加·戴爾.試聽教學法[M].中華書局，1949.

[3]曹一鳴.數學實驗教學模式探究[J].課程·教材·教法，2003（1）：46-48.

[4]李海軍.讓數學實驗有效地進入課堂[J].中學數學教學， 2014（2）：24-26.

[5]李生，徐瑢.基于現代信息技術的數學實驗課初探[J].教育研究與評論（中學教育教學版），2017（1）：71-75.

編輯 李燁艷