一種高精度加權最小二乘算法

王向陽， 蔡成林， 張文波， 蔡 勁

(桂林電子科技大學 信息與通信學院，廣西 桂林 541004)

北斗衛星導航系統是我國自行研制的全球衛星導航定位系統，廣泛應用于交通運輸、海洋漁業、水文監測等領域[1]。隨著北斗衛星導航系統建設的快速發展，國內外學者對接收機鐘差、電離層、對流層等相關誤差進行了研究，分析并糾正了相關誤差后，評估了偽距單點定位的精度。傳統的偽距單點定位算法有最小二乘(least square，簡稱LS)算法[2]、高斯牛頓迭代最小二乘(Gauss-Neton iterative least square，簡稱GNILS)算法[3]、Kalman濾波算法等。由于GNILS算法的定位精度較LS算法高，目前偽距單點定位普遍采用GNILS算法。利用GNILS算法進行定位解算時，對觀測站坐標的初始值的依賴性較大，若選取觀測站坐標的初始值與真實值存在較大偏差，迭代次數將會增加，計算量也隨之增加[4]。鑒于此，提出了一種不等權的自適應加權最小二乘(adaptive weighted least squares，簡稱AWLS)算法。通過北斗實測數據驗證表明，AWLS算法計算復雜度低，定位精度高，并能有效地排除誤差較大衛星對定位平穩性的破壞，有利于接收機實現高精度的定位和導航，可提高偽距單點定位的精度。

1 GNSS偽距單點定位原理

在偽距單點定位的過程中，電離層延遲誤差、對流層延遲誤差、接收機鐘差等因子會對定位結果造成較大影響[5-7]，因此將偽距的觀測方程設為：

(1)

其中：

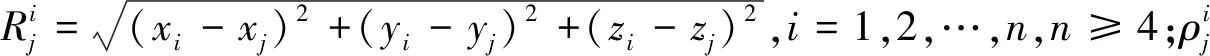
針對以上參數誤差，衛星鐘差dti可通過星歷參數進行修正；電離層延遲誤差dion,j可通過模型進行修正；對流層延遲誤差dtrop,j可通過Saastamoinen模型進行修正[9-11]。誤差修正后的偽距方程為：

(2)

式(1)減式(2)可得Δρi=-(dρi+ερ)。

2 GNILS算法

GNILS算法作為傳統的北斗偽距單點定位算法，在進行定位解算時，根據已知的初始估計值來求解多元非線性方程組，將各個非線性方程在初始估計值處線性化，再根據LS算法原理求解線性化方程，得到解的更新值，并重復這種運算逐次迭代，直至所得結果達到所要求的精度，進而求解接收機的位置坐標[12]。

式(2)的原型為ki=ri0+cdt-ρi，由于Δρi=-(dρi+ερ)非常小，可假設其為零，則式(2)可簡化為：

ki=Ixi·Δxj+Iyi·Δyj+Izi·Δzj-cdt。

(3)

其中：

根據最小二乘原理，得

Δx=(GΤG)-1GΤB。

(4)

其中：

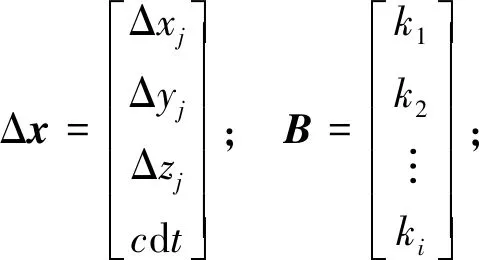
(5)

求出4個估計量(Δxj,Δyj,Δzj,cdt)，更新X0=(x0,y0,z0,B0)，令x0=x0+Δx，y0=y0+Δy，z0=z0+Δz，B0=B0+cdt，重復上述過程進行迭代，直到Δxj,Δyj,Δzj滿足：

(6)

設定一個閾限值α，其取值8～15，迭代次數不超過10次，當式(6)成立時，解算出來的值即為GNILS算法求解出的用戶接收機坐標和接收機鐘差[13]。

3 AWLS算法

AWLS算法與GNILS算法相同的是都需要進行算法迭代，不同之處在于是否構建加權系數矩陣。用AWLS算法構建加權系數矩陣的方法如下：

對于式(2)的原型，

ki=ri0+cdt-ρi

的前2項

ri0+cdt=

其為線性化后的偽距值，后一項ρi為修正后的偽距，雖然后者在實際情況中修正并不完全，還存在一些誤差，但這些誤差相對ρi本身來說是一個非常小的量，即ρi為第i顆衛星與用戶實際位置相對應的含有較小誤差的偽距，ki為第i顆衛星與接收機實際位置相對應的含有較小誤差的偽距與線性化后的偽距之間的偏差。設k為所有可用衛星與用戶實際位置相對應的含有較小誤差的偽距值與線性化后的偽距值之間的偏差，令

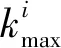
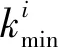
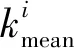
(7)

定位結果最佳。

AWLS算法構造的權系數矩陣Γ是以衛星與接收機實際位置相對應的含有較小誤差的偽距與線性化后的偽距之間的偏差ki為基礎的，它是一個自加權矩陣，隨著迭代的進行，會隨接收機位置的更新而改變。利用此原理，該矩陣能夠極大地降低問題衛星對定位結果的影響，使定位結果更佳。

根據加權最小二乘算法原理：

Δx2=(GΤΓG)-1GΤΓB，

(8)

求出4個估計量(Δxj,Δyj,Δzj,cdt)，更新X0=(x0,y0,z0,B0)，令x0=x0+Δx，y0=y0+Δy，z0=z0+Δz，B0=B0+cdt，重復上述過程進行迭代，直到Δxj,Δyj,Δzj滿足：

(9)

設定一個閾限值β，其取值范圍8～15，迭代次數不超過5次，當滿足式(9)時，解算出來的值即為AWLS算法求解出的用戶接收機坐標和接收機鐘差。

4 算例評估

通過對北斗數據進行分析與仿真來驗證AWLS算法的優越性，其中北斗數據從安裝于桂林電子科技大學的清華高精度接收機中獲取，采用的是2018年3月14日到2018年3月18日的BDS數據，該數據是以30 s為一歷元并連續接收24 h。

在進行定位解算時，考慮到較好的衛星高度角可在一定程度上降低多路徑效應等因素對定位精度的影響，設置衛星的截止高度角為15°。通過多次實驗驗證，衛星的截止高度角為15°時，接收機可接收到足夠多的可用衛星數，且定位精度最優。對BDS數據進行處理分析，通過星歷參數和相應的簡單算法求解衛星的位置，通過Klobuchar模型對電離層延遲進行修正，Saastamoinen模型對對流層延遲進行修正等，進而得到修正后的偽距[14]，如表1所示。利用上述算法得到的衛星的位置坐標、修正后的偽距，通過LS算法、GNILS算法、AWLS算法求解用戶接收機的水平定位精度、高程定位精度、三維定位精度[15]，所得結果如表2所示。

由表2可得以下結論：

1)AWLS算法和GNILS算法相比于LS算法，抗差性能和定位精度都有較大提高；

2)AWLS算法相比于GNILS算法迭代次數少，計算復雜度降低；

3)AWLS算法相比于GNILS算法,抗差性能和定位精度提高約2倍。

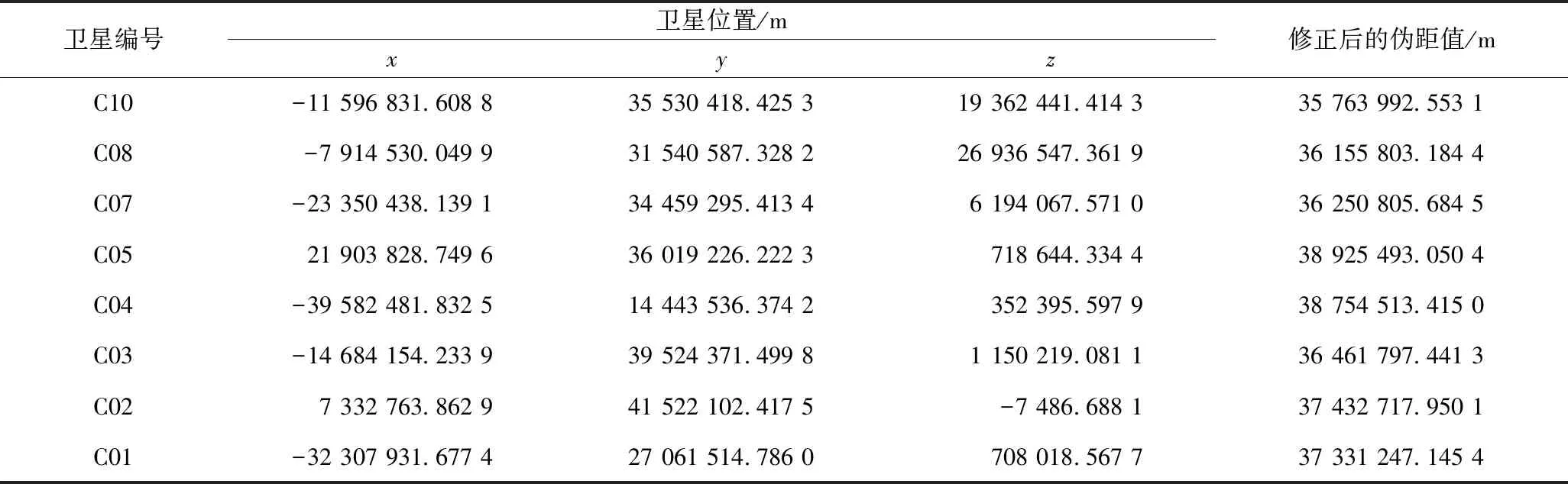
表1 某個歷元的衛星位置坐標和修正后的偽距值

表2 三種算法的定位結果比較

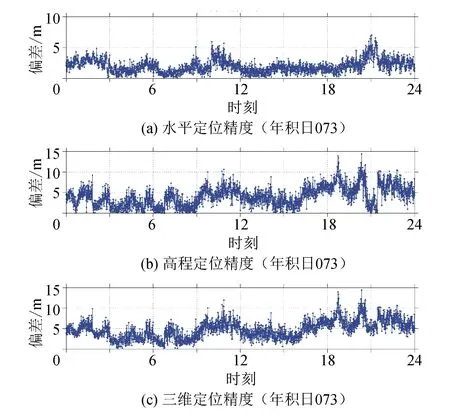
圖1 GNILS算法定位結果

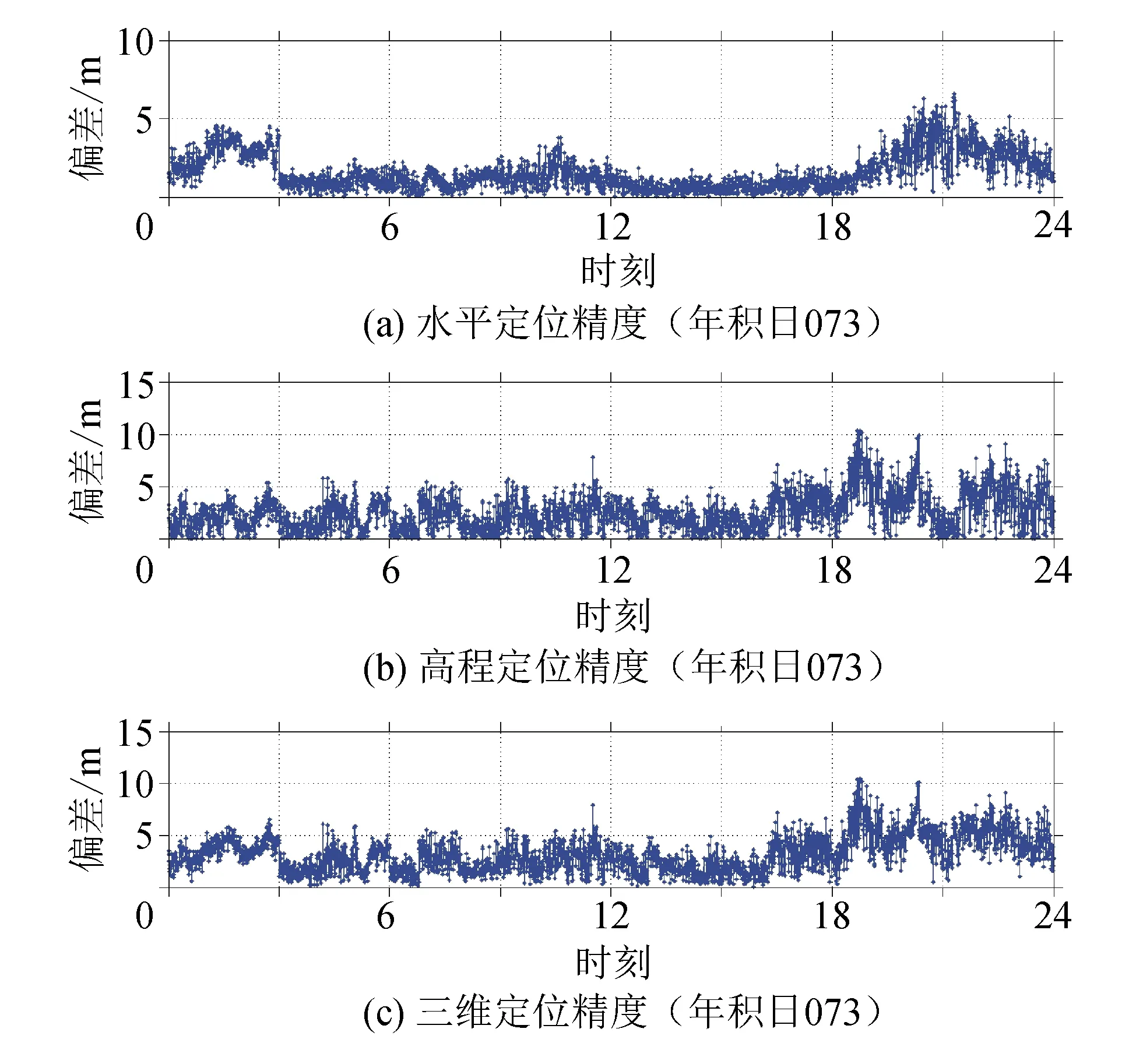
圖2 AWLS算法定位結果

從圖1、2可看出，AWLS算法的定位精度比GNILS算法高，且抗差性能更好,但在18-24這個時間段，幅度較大，精度稍差，但總體來說，AWLS算法相對于傳統的LS算法和GNILS算法較優。

5 結束語

在分析最小二乘法(LS)和高斯牛頓迭代最小二乘算法(GNILS)的基礎上，提出了一種改進的高精度的加權最小二乘(AWLS)算法，并在北斗PVT性能測試評估中進行仿真。該算法利用偽距偏差最大的衛星在定位解算中的權重盡可能小的原理構建一個自加權矩陣，解決了異常衛星對定位平穩性破壞的問題，并極大地提高了定位精度，使北斗偽距的單點定位精度提高到約3 m。