基于深度濾波器優化的SLAM單目稠密重建*

楊海清, 曾俊飛

(浙江工業大學 信息工程學院, 浙江 杭州 310000)

0 引 言

同時定位與地圖構建(simultaneous localization and mapping,SLAM)指搭載特定傳感器的主體，在沒有先驗環境信息條件下，通過自身運動的過程來建立所處環境的空間模型，同時估計自身的運動軌跡。當傳感器為相機時，稱之為“視覺SLAM”。根據使用視覺傳感器的數量和類型的不同，視覺 SLAM 系統主要可分為3 類:單目視覺SLAM、多目視覺SLAM和RGB-D SLAM[1]。

重建稠密地圖是視覺SLAM的兩大目標之一，使用RGB-D相機進行地圖重建是目前的主流方法[2]，但是RGB-D相機存在測量范圍窄、噪聲大、視野小、易受日光干擾等諸多問題，主要適用于室內環境。而雙目相機的配置與標定較為復雜，其深度量程和精度受雙目相機的基線與分辨率所限。對此，本研究選用單目相機傳感器，其結構簡單，成本較低，環境適應性較強，且抗干擾能力顯著。當單目相機移動時圖像會形成視差，利用視差可獲取像素的深度信息[3]。因此，SLAM系統使用了一種既節省計算量還可使估計的地圖點更為準確的方法——深度濾波，通過深度濾波可計算出真實地圖點最有可能存在的坐標位置[4]。

無論哪種工業機器人，想要完成準確跟蹤定位、精確導航、實時避障和完美還原三維場景的任務，都需有高精度的稠密地圖[5]。但是，由于單目相機圖像像素可能出現誤匹配，且傳感器噪聲和環境噪聲時刻存在，總是會形成一些誤差極大甚至假的地圖點，導致稠密地圖重建準確率不高。因此，為提高單目相機恢復原始場景的能力，本文提出了一種基于深度濾波器優化的稠密重建算法，旨在獲取重建準確率更高、表面更加細膩的三維稠密地圖。

1 地圖重建系統的總體框架

系統的框架主要由三大部分組成，包括：關鍵幀選取與匹配像素點對、深度濾波技術和稠密建圖。具體模塊如圖1所示。

圖1 地圖重建系統總體框架

首先，系統對關鍵幀數據進行極線搜索，采用像素塊匹配策略來提高匹配準確率；其次，利用三角化測量獲取像素的深度數據，使用濾波器技術對深度數據進行跟蹤并融合，實現高效的場景重建；最后，本文綜合考慮因光照、遮擋、運動模糊等原因引起的深度值錯誤估計，顯式處理外點，采用優化后的算法對每一像素點的深度估計值進行監控，及時剔除異常深度值，對深度圖中相鄰像素深度變化過大的情況進一步判斷與處理，保證稠密地圖的重建準確性。

2 基于深度濾波技術的稠密重建

2.1 稠密地圖前端預處理

重建稠密地圖，需估計每一個像素點的深度值，如若利用地圖中每個像素點的描述子進行匹配，會在前端階段占用大量的工作時間，這在實時性要求較高的SLAM系統里是不允許的。因此，采用極線搜索[6]和塊匹配技術[7]來確定第一幅圖像中像素在其他關鍵幀的位置，如圖2所示。

圖2 極線搜索示意

左邊相機O1觀測到參考幀IR存在像素點PR，假設其深度存在的范圍區域是最小值dmin到無窮大，即該像素點到對應空間點的距離為圖2中的d射線。d射線的投影在當前幀IC上形成一條線，為極線l1，在極線上比較每個像素與PR的相似程度。

本研究采用比較像素塊的方法，以提高像素匹配的區分性。先在PR周圍選取一個w×w大小矩形窗口W1，再在極線l1上取多個同樣大小的矩陣塊進行比較，把PR周圍的矩形窗口記為W1∈Rw×w，極線l1上的n個小塊記為Wi∈Rw×w(i=1,2,…,n)。計算矩形窗口W1與Wi的相似性，采用去均值的NCC方法[8]，即

S(W1,Wi)=

(1)

式(1)的結果接近于0時表示兩個矩陣塊不相似，接近于1則代表相似。

此外，利用仿射矩陣獲取到更佳的像素匹配結果[9]，并由像素匹配點對估計出當前幀像素深度值，定義為

dRPR=dCRPC+t

(2)

式中R為旋轉矩陣，t為平移向量。式(2)兩端同時左乘PR的反對稱矩陣M可求得當前幀像素深度dC。

2.2 基于均勻—高斯濾波的稠密重建算法

前端預處理階段提供深度初值，后端濾波器負責對這些數據進行深度融合。均勻—高斯濾波算法[10]采用高斯濾波[11]跟均勻濾波相結合的方法，對同一空間點投射在不同關鍵幀的像素點深度值進行概率統計分析，不斷融合更新深度圖。如圖3所示。

圖3 深度圖融合更新過程

圖3中，Zk-1是k-1時刻狀態的深度值，dk是k時刻的深度估計值。以此類推，可以獲取k+n時刻狀態的深度值。均勻—高斯濾波器算法模型如下

(1-p)u(μobs|μmin,μmax)

(3)

記均勻分布中上一個狀態的參數為aest,best，由新的觀測數據計算得到的參數為a,b。經過融合更新后的深度值和方差為μupdate,σupdate,均勻分布的參數變為aupdate和bupdate。深度融合過程如下

(4)

計算權重系數C1，C2

(5)

計算U1，U2來更新均勻分布的系數a，b

(6)

進而，深度融合后的均勻分布系數分別為

(7)

融合后像素點的深度值為

μupdate=C′1*m+C′2*μest

(8)

融合后深度值的方差為

(9)

隨著深度的融合，像素深度值方差逐漸收斂，當方差保持收斂不變時，則停止對該像素點更新融合，并將深度值記錄為真實值。反之，如果深度值的方差經過若干次融合后反而變大，則判斷該像素點為外點，將其剔除，并停止更新融合。當所有像素點停止融合時，算法完成場景的稠密重建工作。

3 基于簇的均勻—高斯濾波算法改進

均勻—高斯濾波算法對圖像各像素點獨立計算深度值，由于像素匹配多義性、噪聲等問題的存在，造成相鄰像素深度相差過大，算法在遇到弱紋理、傾斜表面等區域時，場景的重建完整性仍存在問題。本文算法對均勻—高斯濾波算法進行改進，在正確處理外點的基礎上，構建了用于深度值優化的聚簇分類，簇結構可表征場景的空間平面幾何關系，在簇內進行深度值優化可更好重現場景的三維結構。

3.1 簇類劃分

均勻—高斯算法實時更新深度圖，使用簇類劃分對每個時刻更新的深度圖進行跟蹤，將具有相似特性的區域劃分為同一個簇，在簇內對深度值進行優化處理。基于簇的深度更新流程如圖4所示。

圖4 基于簇的深度更新流程

將深度圖均分為400個區域，區域中心像素作為初始種子點，篩選種子點的條件為

λσi<σ

(10)

式中σ為所有像素的深度方差，σi為第i區域內像素的深度方差，λ為自適應閾值，由σ的大小情況而決定。

將篩選后的種子點深度值作為初始均值向量μ={μ1,μ2,…,μi,…,μN}其中N為篩選后的種子總個數。根據劃分規則將像素xi劃入相應的簇C={C1,C2,…,Ci,…,CN}，簇類劃分規則定義為

(11)

式中μi為第i個簇的深度均值，xμ為第i個簇中心像素的位置，di為第i個像素的深度值，xi為對應的像素位置。T1為像素距離閾值，T2為深度閾值。將滿足式(11)的像素落入相應的簇，未落入任何簇的像素標記為外點，并剔除外點此次狀態深度值。

所有像素劃分完成后重新計算簇的深度均值，定義為

(12)

式中d為像素深度，|Ci|為簇Ci內像素總個數。更新當前均值向量和簇的中心像素位置后，重復執行上述過程，直至所有簇更新很小甚至不再更新或者達到最大迭代次數，則終止迭代，進而得到簇劃分。

3.2 簇內優化

簇內優化算法如下：

2)若選取的圓上有連續12個像素點深度大于du+T3或者小于du-T3(實驗中閾值T3設置為du的10 %)，則以該像素點為圓心，選取半徑為1個像素大小的圓上的8個像素點；

3)將圓上的8個像素點深度均值作為像素點u的深度值，若像素點u為邊緣像素或者圓內包含其他簇的像素時，則對像素點u的深度值不進行處理；

4)循環執行以上三步，對圖像中每一個像素執行相同的操作。

深度校準示意圖如圖5所示。

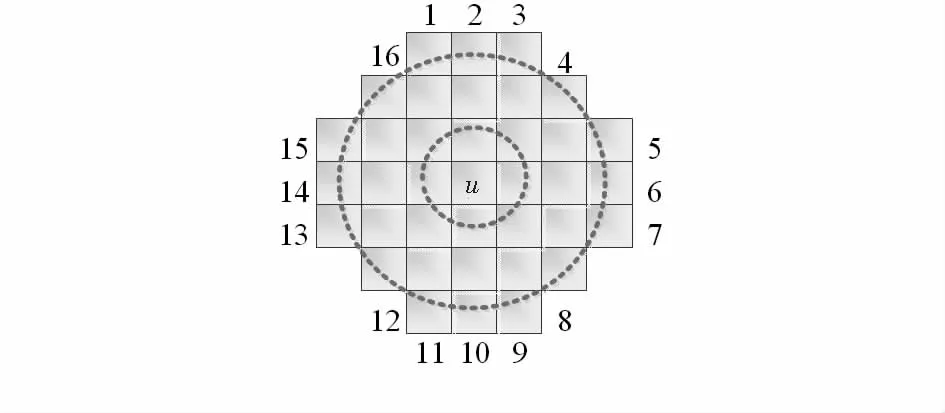
圖5 深度校準示意

故此，采用改進的均勻—高斯濾波算法觀測每一時刻的深度圖，為后續的深度融合提供精確的深度值，極大避免了像素匹配錯誤、深度值估計錯誤所帶來的誤差，使得重建的稠密地圖更加平滑細致。

4 實驗結果與分析

為了驗證本文算法的有效性和可行性，實驗中使用了公共圖像幀數據集進行測試。測試數據集包含Remode數據集、Valbonne數據集和Wadham數據集[12]，三個公共數據集的真實場景圖像如圖6所示。實驗環境為：Intel 八核計算機，8 GB內存，Windows 64操作系統；算法在Ubuntu14.04系統[13]中進行實現，采用了C++語言和Opencv庫[14]。

圖6 公共數據集原圖

本文分別采用高斯濾波器、均勻—高斯濾波器和改進型高斯濾波器三種深度濾波算法對測試數據集進行試驗來獲取評測數據，評測指標包括地圖的重建情況和重建準確率。實驗結果如圖7所示。

圖7 稠密重建地圖

Valbonne數據集背景為天空，深度距離較遠，Wadham數據集建筑物包含大量細節，各細節深度相差較小，這些圖像特點都會對深度估計造成影響。由圖7(a)可知，高斯濾波器對三個數據集的深度估計大致正確，但也存在較多的錯誤估計，其表現為地圖中很多像素點與周圍像素點深度不一致，而位于邊緣區域的深度也沒有得到正確估計。均勻—高斯濾波器將內點和外點進行區別處理，正確處理錯誤匹配的像素點，圖7(b)的三張地圖相比圖7(a)更為平滑，但在物體與天空的邊緣區域仍存在較多地錯誤估計。從圖7(c)中可以明顯看出，改進型算法對三個數據集的物體邊緣區域進行正確處理，剔除錯誤估計的深度數據后，重建的稠密地圖比其他兩種濾波算法重建的地圖更加符合實際的三維場景。

將重建的稠密地圖與原圖進行比對，獲取重建后的有效特征匹配對。各測試數據集在各算法上的平均有效特征匹配對如表1和圖8所示。圖8中的1,2,3分別表示基于改進型均勻—高斯濾波器、均勻—高斯濾波器以及高斯濾波器的特征匹配對數量。

圖8 改進型均勻—高斯算法重建的稠密地圖有效特征點相對于其他算法的增長比例

由表1數據和圖8可知，改進型均勻—高斯算法重建的稠密地圖有效特征點大幅增加，稠密度增高，原算法中存在空洞的區域在算法改進后空洞變小。

表1 不同算法的特征匹配對數量對比

為了進一步衡量本文算法的有效性，需定量比較三種濾波算法的重建準確率[15]。記重建準確率為R，參考幀及其相鄰的K-1個關鍵幀為Ci(i=1,2,…,k)，關鍵幀的全部像素點集合為P，關鍵幀中某一像素點u(u∈P)對應的實際深度值記為Z(u,Ci),由濾波器估計得到的深度值記為Zest(u,Ci)。當像素點u在N個相鄰關鍵幀中都符合這個條件，則認為像素點u的深度值估計成功。故準確率R可定義為

(13)

式中 函數f在括號內條件為真時為1，反之為0，μ為深度值差異閾值，實驗中N設置為6。重建準確率對比情況如表2所示。

表2 稠密重建準確率比較

從表2可以看出，本文提出的改進型均勻—高斯濾波器算法在三個測試數據集上的稠密地圖重建準確率分別為0.836 2，0.803 4和0.843 7，各個數據集的重建準確率相比于高斯濾波和均勻—高斯濾波這兩種深度濾波方式分別提高了約30 %和10 %。顯然，改進型算法無論是在室內場景還是在復雜環境的室外場景，都表現出較強的深度濾波能力，說明該算法在單目稠密重建地圖方面有著較顯著的有效性和較高的準確性。

5 結束語

稠密建圖是視覺SLAM的主流建圖方式之一，其廣泛應用于各項工業任務中。針對高斯濾波算法重建稠密地圖存在像素點誤匹配、重建準確率不高的問題，本文提出了一種基于簇的均勻—高斯深度濾波算法，將深度估計值從一個非常不確定的值逐漸逼近到一個穩定值，重建出更加準確的三維稠密地圖。實驗結果表明，本文算法在不同環境下的數據集中都表現出較強的適應性，能較好地處理弱紋理區域、光照遮擋區域和弧面區域中存在的深度錯誤估計問題，并實時剔除外點數據，優化簇內深度值數據，在三個數據集上的重建準確率都高于高斯濾波算法和均勻—高斯濾波算法，重建的稠密地圖也比其他兩種算法更加準確、細致。在下一步工作中，將根據圖像顏色分布情況和幀間變換信息，進一步改進復雜環境的深度估計，構建更加完善的稠密地圖。