壓電陶瓷執行器的動態遲滯非線性特性建模*

潘云鳳, 潘海鵬, 趙新龍

(浙江理工大學 機械與自動控制學院, 浙江 杭州 310018)

0 引 言

隨著微/納米技術的迅猛發展，智能材料如壓電陶瓷[1]，超磁滯伸縮材料[2]，形狀記憶合金等材料的執行器，已經應用在光學精密加工工程、微電子制造技術、航天航空技術、超精密機械制造、微機器人操作、生物工程等領域，并且正逐步推廣到更多領域。但執行器輸入輸出表現為非光滑，多值映射的遲滯特性[3]不僅會使系統的控制精度降低，甚至會導致系統不穩定，大大局限了其發展。

Hammerstein模型可以描述遲滯的動態特性，它由一部分非線性靜態模型和一部分線性動態模型組成，結構相對簡單，且辨識方法多樣。向微等人[4]將Hammerstein模型的線性動態部分和非線性靜態部分分別用Laguere級數和非線性基表示,辨識得到兩部分的參數，此外，智能算法如神經網絡[5]、支持向量機(support vector machine,SVM)[6]也已用于Hammerstein模型的辨識，使Hammerstein遲滯模型的辨識過程變得更加簡便。但對于壓電陶瓷執行器的遲滯特性來說，如何使神經網絡類的模型接受遲滯的多值映射性成了辨識難點。Zhang X L[7]等人提出了基于擴展空間辨識法的神經網絡辨識法，結合Hammerstein模型得到了率相關遲滯的模型，謝揚球[8]等人也同樣運用了擴展空間法來構建神經網絡，所不同的是他重構了遲滯信號以消除Hammerstein中間信號不可測的問題。神經網絡方法需要設計網絡結構，且容易陷入局部最優，還存在一系列過擬合問題，為此Goethals I[9]將最小二乘支持向量機應用于Hammestein模型。徐運揚[10]等人還將支持向量機結合了奇異值分解進行壓電陶瓷類遲滯的辨識。

本文利用優化的支持向量機逼近一種新的Backlash遲滯因子建立靜態的遲滯非線性模型，再運用Hammerstein結構，引入動態環節來實現動態遲滯建模。本文的創新之處在于：將一種Backlash描述函數算子引入了Hammerstein模型，來提取遲滯環的特征，與萬有引力搜索算法優化的支持向量回歸機結合來建立靜態模型，訓練速度快，收斂性強，并用ARX(自回歸各態歷經)模型實現了動態建模，很好地體現了遲滯的率相關特性，最后用實測數據對模型效果進行了證明。

1 一種Backlash描述函數類遲滯因子

為了將靜態遲滯的多值映射特性從系統中解耦出來，變成一一映射，本文將引入一個新穎的遲滯因子來描述遲滯的“上升”，“下降”，“轉折”的過程等，此算子提取了大部分遲滯非線性的信息，能夠比較好地勾勒遲滯非線性的輪廓。

首先介紹Backlash模型的描述函數[11]，令輸入x為幅值為A的標準正弦曲線

x=Amaxsinθ，θ=ωt

Backlash的特性方程可用式(1)，式(2)表示

(1)

(2)

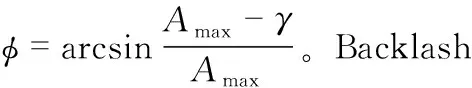
上述標準的Backlash算子加權求和可得到一般遲滯模型[12]。但對于非常規，非平滑的遲滯非線性來說，Backlash的常規模型精度不高，因此引入了以下的Backlash描述函數類算子。

根據諧波分析原理，忽略二次以上諧波分量可得Backlash模型的描述函數

(3)

復數域的計算提高了建模復雜性，所以,由一次諧波分量的定義方式啟發,構造

g(θ)=Psinθ+Qcosθ

(4)

(5)

(6)

式中P和Q分別為描述函數的實部和虛部，顯然，P關于b對稱且單調減小，P∈(0,1),Q≤0，再定義

F(θ)=d·arctan[c·(Psinθ+Qcosθ)]

(7)

式中d,c為函數F(θ)的增益。c控制遲滯特性的大小，γ控制遲滯環的寬度，d控制遲滯環的高度。定義F(θ)為基于Backlash類算子的基本遲滯函數。

采用電容傳感器獲取壓電陶瓷輸入電壓，驅動電壓為幅值為1.5V的正弦波，頻率為3 Hz，建立的Backlash描述函數算子如圖1所示，疊加單個Backlash描述函數算子可對應不同形狀的遲滯環，算子可較好地描述給定輸入下遲滯單環的靜態遲滯特性。

2 動態遲滯特性的Hammerstein模型與辨識

2.1 Hammerstein遲滯模型結構

考慮壓電陶瓷執行器的機理結構，其電壓—位移特性可用Hammerstein塊狀系統[13]來描述，分為靜態非線性環節和動態線性環節，再進行串聯，其中靜態非線性環節用來體現壓電陶瓷執行器的靜態遲滯非線性，動態環節用來體現系統的動態特性，此動態特性表現為系統輸出與輸入信號速率有關。壓電陶瓷執行器的Hammerstein系統結構如圖2所示。

圖2 Hammerstein塊結構系統

圖2中H(·)為遲滯非線性部分，M(·)為線性動態部分，其中，u(t)為輸入信號，v(t)為經過H(·)這個遲滯環節后得到的中間變量，y(t)為經過線性動態環節后Hammerstein系統的輸出，即執行器的位移估計量。為了構建Hammerstein模型，需要首先建立靜態遲滯模型，本文中靜態遲滯模型用萬有引力搜索算法(gravitation search algorithm,GSA)優化的SVM描述，但與神經網絡相同，支持向量回歸(support vector regression,SVR)同樣只接受一一映射的數據集，因此,采用上文的Backlash描述函數算子與優化SVM混合建模。動態線性部分則由ARX模型描述。

2.2 Hammerstein靜態遲滯部分建模

本文采用GSA優化的SVR來逼近Backlash描述函數算子，可將遲滯的多值映射轉變為一一映射，從而建立Hammerstein模型的靜態遲滯部分。

由于最小二乘支持向量機(least square support vector machine,LSSVM)關鍵的模型參數a非常稠密，使得支持向量數量多，模型復雜度高，降低了小樣本數據的建模效率，一定程度上失去了解稀疏性的特點，因此這里采用不敏感損失函數——SVR(ε-SVR)算法來建立靜態遲滯模型，同時，懲罰系數C和采用的徑向基函數(radial basis function,RBF)核參數σ，二者的取值對SVM的逼近效果有很大的影響，本文引入了一種GSA來優化ε-SVR。

實驗所用訓練集可寫為

(8)

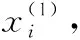
(9)

ξi≥0,i=1,2,…,N

式中C為懲罰系數，ξ為松弛因子，Φ(x)為x的映射空間。ω項表征擬合誤差的大小，ξ項表征模型復雜度，懲罰系數C可平衡二者。構造Lagrange函數求解

(10)

式中ai≥0，μ≥0，ai,i=1,2,…,l為拉格朗日乘子。

運用KKT(Karush-Kuhn-Tucker)最優化條件,整合優化問題成為如下線性方程組

(11)

化簡可得

(12)

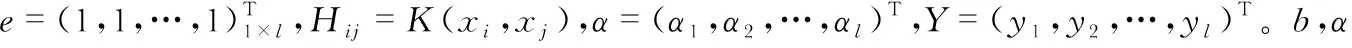
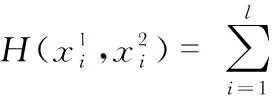
(13)

式中K(x,xi)稱為核函數。本文實驗取RBF核函數K(x,xi)=(-(xi-xk)2/2σ2)。

核參數以及懲罰系數不同的選取影響了系統模型的性能，因此本文采用GSA對參數和C進行優化選取。GSA是一種由自然界中萬有引力使粒子不斷靠近的現象啟發而成的智能算法。現將樣本點假設為粒子

(14)

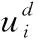
(15)

(16)

靜態遲滯部分建模步驟如下：

2)將算子輸出與輸入電壓通過GSA-SVR模型：按式(14)、式(15)進行更新直到算法收斂，得到SVR的最佳參數，訓練SVR模型H[x(t),F(θ)]，得到靜態遲滯輸出的估計值，即為Hammerstein模型的中間變量v(t)。

3)記錄GSA和SVR的模型參數C，σ，a，b即為靜態遲滯模型參數。

2.3 Hammerstein模型動態部分建模

ARX模型[14]是一種有理傳遞函數模型，本文用ARX模型表征壓電陶瓷執行器的動態線性部分。

ARX動態線性部分模型可寫為

A(z)y(t)=B(z)v(t)+e(t)

(17)

式中e(t)為系統誤差A(z)=1+a1z-1+…+anz-n,B(z)=b0+b1z-1+…bmz-m為單位延遲算子。將ARX模型寫為傳遞函數形式

M(z)=B(z)/A(z)

(18)

動態部分建模步驟如下：1) 壓電陶瓷執行器輸入1～100 Hz掃描正弦數據，按式(6)算出所對應的Backlash類算子的輸出值；2) 將算子輸出和輸入數據通過靜態部分辨識得到的GSA-SVR模型，得到中間變量v(t)；3) 基于實際的遲滯輸出位移和中間變量v(t),可用遞歸最小二乘法辨識出ARX模型的傳遞函數。

2.4 Hammerstein模型建模整體框架

壓電陶瓷執行器的Hammerstein模型整體可寫為

(19)

整體辨識方案如圖3所示。

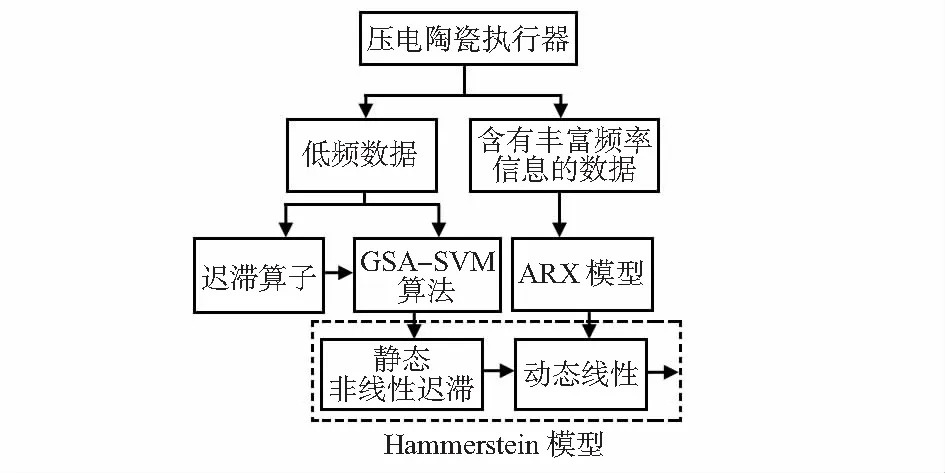
圖3 整體辨識框架

3 仿真實驗

采用壓電陶瓷執行器PZT—753.21C(PI公司產品)來驗證本文所提出的遲滯模型的性能。該執行器在輸入電壓0～100 V下，額定位移為0～25 μm，采樣頻率為30 MHz。測得的數據經過濾波后，采用10 000個數據，將這些數據平均(間隔)分成兩部分，5 000個用于逼進遲滯曲線，5 000個用于模型驗證。

實驗參數設定如下：Backlash算子參數：K0=1,Amax=1.5，c，d=1，b=1/36～1，w=6π,n=36。SVR算法參數：ε設置為0.01。GSA算法參數：群體規模20，最大迭代次數為50。GSA優化結果為C=76.102 4，σ=7.132 2。

遲滯特性在低頻時(小于5 Hz)動態線性部分基本忽略率相關性，此時的辨識結果如圖4所示。

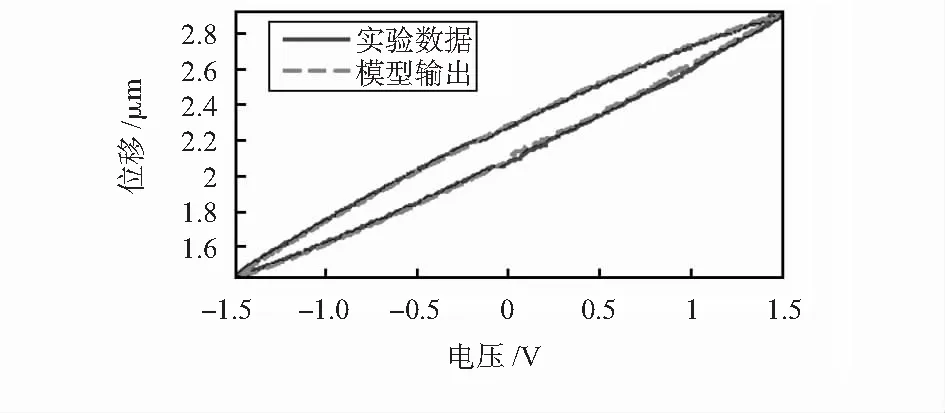
圖4 低頻靜態遲滯辨識曲線

ARX模型的階數可采用赤池信息準則(Akaike information criterion，AIC)[15]來確定，由于系統動力學特性一般可由質量—彈簧—阻尼系統表示，因此,經過多次實驗，辨識得到的階次均為2階。辨識出的二階系統為

(20)

給壓電微動臺輸入50 Hz正弦電壓，獲取5 000個數據來驗證所提出的模型，輸出位移量及遲滯環擬合曲線、誤差曲線如圖5所示。

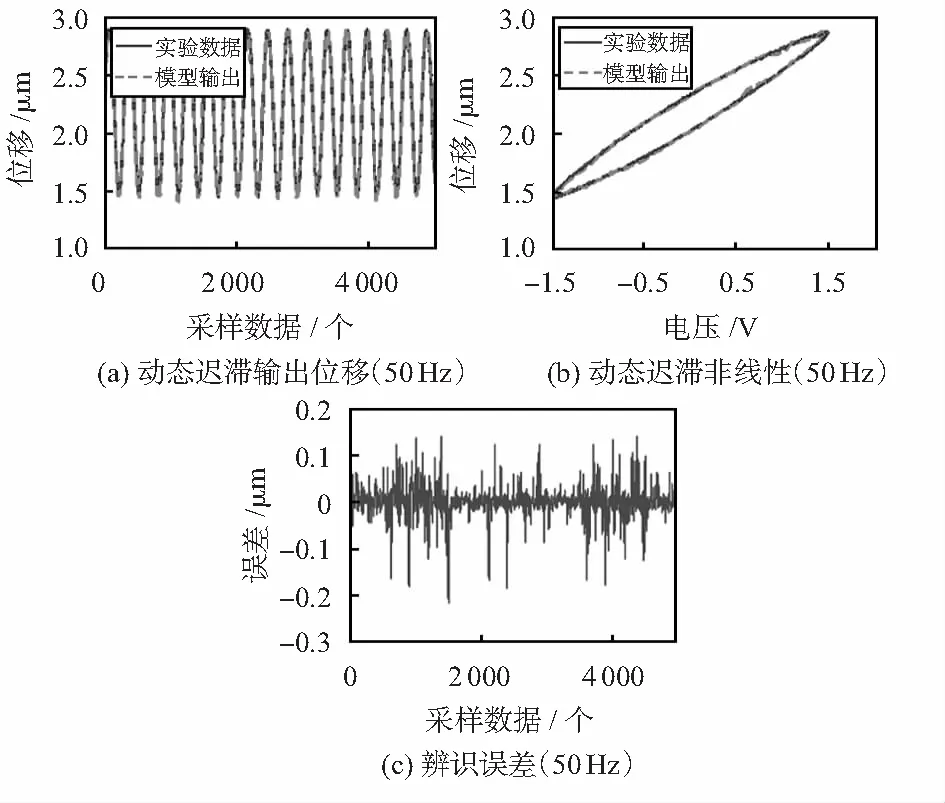
圖5 50 Hz遲滯數據檢驗結果

由圖6分析可知，建模預測位移值與期望位移值偏差較小，相關性很強。再以均方根誤差(root-mean-square error,RMSE)、相對誤差(relative error,RE)及R2作為評價標準，公式如下

(21)

得到的MSE為0.008 0，平均RE為1.43 %，R2為0.999 4,最大建模誤差為0.053 2 μm。

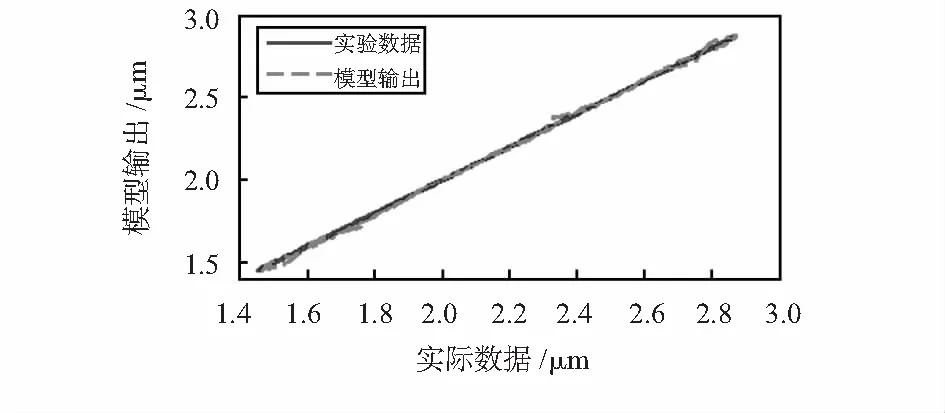
圖6 線性相關曲線

4 結束語

采用Backlash描述函數模型對靜態遲滯環進行了擬合，將算子輸出與輸入電壓一起放入SVM模型，從而將遲滯的多值映射特性變為一一映射，由于SVM本身的缺陷，本文采用了GSA算法對SVM進行了優化，SVM的模型輸出即為Hammerstein級聯結構的中間變量，再通過ARX模型，就可以對遲滯的率相關特性進行描述，所提出的方法的性能通過數值模擬進行了證明。結果表明，所提方法建立的模型與實際模型擬合度好，并且建模速度快。