一堂“意外”的數學課

張雄波

由于數學課的開放性很強，我們的學生又是一群活潑可愛的少年，因此數學教學過程中也充滿了太多的不確定因素。我們在備課中的一些預設，并非會按照我們設想的那樣去完成。作為教師的我們在課堂上充滿了太多的挑戰。這需要教師有一雙慧眼，能捕捉到課堂中有價值的信息，并將這種信息合理的，有效的利用，讓課堂中的意外變成教學中的精彩。

八年級數學12.2.1作軸對稱圖形的最后一個內容是“探究”問題，我在課堂上經歷了一系列意外，促成了良好的教學效果，自己對探究課的意義及組織有了更深的認識，現把課堂教學過程實錄如下。

課本第42面給出了探究內容：

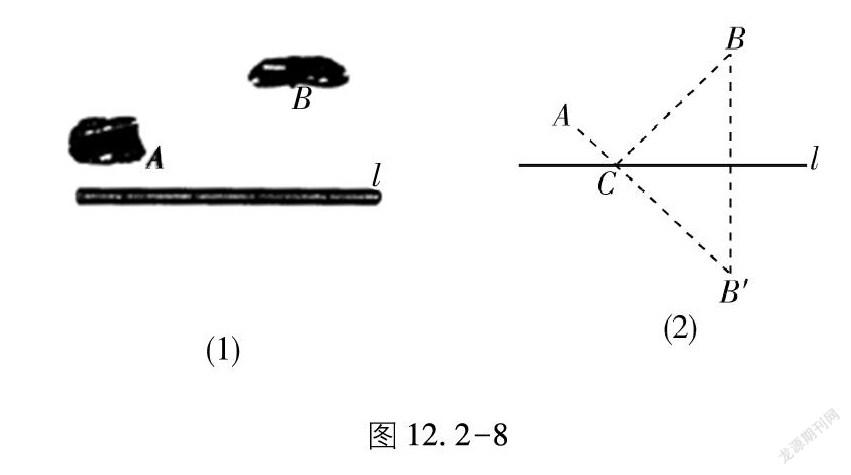
如圖12.2-8（1），要在燃氣管道l上修建一個泵站，分別向A，B兩鎮供氣.泵站修在管道的什么地方，可使所用的輸氣管線最短？

你可以在l上找幾個 試一試，能發現什么規律？

我們可以把管道l近似地看成一條直線，A，B兩鎮近似地看成兩個 （圖12.2-8（2）），問題就是要在l上找一 C，使AC與CB的和最小.設B′是 B關于直線l的對稱 ，本題就是要使AC與CB′的和最小.在連接AB′的所有線中，線段AB′最短.因此，線段AB′與直線l的交 C的位置即為所求.

為了證明 C的位置即為所求，我們不妨在直線l上任取一 C′（不與C重合），連接AC′，BC′，B′C′.

因為直線l是 B，B′的對稱軸， C，C′在l上，所以CB=CB′，C′B=C′B′，

所以AC+CB=AC+CB′=AB′.

在△AC′B′中，

由三邊關系可得AB′<AC′+C′B′，

所以AC+CB<AC′+C′B，

即AC+CB最小.

同年級其他班的數學老師教過該節內容，感覺學生似懂非懂。我擔心教學效果差，就向學生強調預習好該節內容。課堂開始，我問：“多少人看懂了？”（沒有一個人舉手應答），氣氛的沉悶讓我意外。就算我講下去，學生也只是被動接受。

我說：“現在同學們在直線l上找個 試下，只要能說出畫法和自認為滿足要求的理由，不要太在乎對錯，更不必受課本解法的影響。”學生行動了，我看到學生甲找了一個 ，就要他發言，甲說：“先連接AB，再作線段AB的垂直平分線交l于 C，在 C處修泵站，理由是垂直平分線的性質：垂直平分線上的 到線段的兩個端 的距離相等。”我一愣，這與問題要求毫不相關，正準備否定，卻聽到有學生發出輕聲同感“我也是這樣做。”這樣一個錯誤的答案也有部分人響應，再次讓我意外。我改變主意（甲正用期盼的眼神望著我），說：“甲勇于探索，找到了一個 ，大家要向他學習，并且他把剛學過的垂直平分線的性質用上了，得CA=CB，是否符合問題的要求，暫時不討論，想問的是，還有誰像甲一樣探索找到了別的 ？”

受甲的鼓舞，乙主動舉手答：“過 A作l的垂線段，垂足為 C，在 C處修泵站，理由是垂線段最短。”我有些高興，因為他的問答與問題的要求近了 ，正要評價（丙急忙舉手，有觀 迫切表達），我稍遲疑，還是讓丙先說。“過 B作l的垂線段，垂足為 C，在C處修泵站，理由是垂線段最短，我用的道理和乙雖然一樣，但我的做法照顧了B鎮的人，畢竟他們離管道l遠些，所以我認為自己的作法更好。”丙的話音剛落，班上馬上出現了兩派，和乙關系好的學生力挺乙的觀 ，丙也有不少擁護者，一時爭論難下，又有學生開始調和：“兩個人的都對。”大家望著我，等我來評判。我說：“大家量一下兩種情況下的CA+CB。”學生在書上畫圖，很快測量出乙的CA+CB=0.6+2.6=3.2 cm，丙的CA+CB=2.2+1.5=3.7 cm（丙的擁護者很失落，但仍有不服氣的神色），丙站起說：“我和乙用的同樣的道理，如果說我的錯，那么他的也不一定對。”新的一輪爭論又開始……，又有學生調和：“就在乙和丙找的兩個垂足之間再找，可能是兩個垂足的中 吧！”甲也說：“我的作法中，C 也在乙和丙的兩個垂足之間，乙和丙不一定對，那么我的有可能對。”沒有統一的觀 ，教室里學生自發的爭論，各抒己見，久違的活躍氣氛讓我意外。（我既欣喜，又焦急，看表已過了近17分鐘，仍沒進入正確的做法和分析，真不知今天的教學任務能不能完成）

不能破壞學生好不容易形成的積極性，我開始引導說：“大家認真思考了，也都有一定的道理，但因為有片面之處難以說服他人，請同學們按我的提示分步進行分析。”教室變得十分安靜，我說：“首先，泵站C的地 有人認為是乙、丙所說的垂足，也有人認為在這兩個垂足之間，都自覺地把C當成了一個動 來研究，請問動 C還會在其他位置嗎？再研究一下。”很快乙舉手答：“如果在我所說的垂足的左邊，CA與CB都會變大，不可能。”丙也舉手答：“如果在我所說的垂足的右邊，CA與CB也都變大，不可能。”我繼續引導：“看來泵站C只能在乙、丙所說的垂足上或兩個垂足之間了，但同學們剛才的討論始終沒有一致結論，是否應該把CA，CB中的一條線段換下位置，再求和的最小值？”（學生若有所思，3分鐘后有學生陸續舉手）在我示意下，丁回答：“我發現課本上把CB換成CB′了。”我問：“B′是怎么作的？CB=CB′嗎？AC+CB′在什么情況下最小？”丁說：“B關于直線l的對稱 是B′。因為對稱的線段相等，所以CB=CB′。A，C，B′共線時，AC+CB′最小，理由是兩 之間線段最短。”（我在與丁的一問一答中，觀察到許多學生緊皺的眉頭舒展開，露出會意的笑容）我問：“聽懂了丁的分析的同學請舉手。”全班學生都自信地舉起手。這又一次讓我意外，難道學生突然變聰明了，可能是他們今天積極思考、聽講認真、學得主動的緣故吧！（我看了下時間，剛過了30分鐘，估計今天的教學任務可完成）

接著，我訓練學生寫出規范的做法，嚴謹的說明過程。接近尾聲，戊舉手提問：“您作的是 B關于直線l的對稱 B′，再連接AB′交l于 C，在 C處修泵站;我認為也可以作 A關于直線l的對稱 A′，再連接A′B交l于 C，在 C處修泵站。那有兩個 C怎么辦呢？”學生們沒想到戊提出個新的答案，又開始議論起來，也有人動筆畫圖。在集體研究中大家發現兩個修泵站的 在作出的圖中竟是重合的。至此問題圓滿解決（距離下課還有5分鐘，我布置了相關練習題，學生們躍躍欲試，后來從作業的批改來看，完成的情況良好）。

一直以來，我自以為對數學問題的理解和分析都很透徹，教學中盡顯自己的主導作用，但效果平平。這堂探究課對學生放手，產生了意外的效果。在本節課初，我檢查預習情況時氣氛的沉悶，甲的錯誤答問讓我意外，但這是班級的現狀，不能回避。我沒有選擇自己主講，也沒有選擇批評學生。接著乙和丙大膽地探究，以及圍繞著兩個人的結論展開的一輪又一輪的討論使學習氣氛異常活躍，讓我意外，這是我的寬容、鼓勵激發了學生潛在的積極性和智慧，出現百家爭鳴的局面。最后，學生的探究活動在老師的引導下達到新的高度，丁給出精彩的回答，戊提出有價值的疑惑，學生接受知識的能力如此之高，又一次讓我意外，這只說明在探究活動中學生一旦真正參與，成為學習的主人，全身心投入，學習就會成為樂趣，既輕松又高效。

探究性教學成為時代寵兒，源于它符合新的教育理念，信任學生的學習能力，營造寬松且不乏競爭性的課堂氛圍，師生積極互動，共同發展，讓學生在探索、討論、實踐、質疑中學習。探究性教學不但讓學生獲得知識，更讓學生獲得學習的能力。我的一堂課意外的良好效果正是一個有力的證據。

葉瀾教授說過：課堂應是向未知方向挺進的旅程，隨時都有可能發現意外的通道和美麗的圖景，而不是一切都必須遵循固定線路而沒有激情行程。因為數學問題的開放性很強，所以數學課堂上的教學中會有很多的不確定性。而且學生也在接受各種各樣的有意義的信息，因此教師對他們的經驗水平、知識積累乃至認知潛能等諸多方面都不可能預設到位，因此教師在課堂上實施的教學過程中充滿了很大的挑戰。這就要求教師用他的智慧將課堂中的一次次意外，轉變成教學中的一次次亮 。

教師在備課時必須要考慮到不同的學生對同一問題可能會有不同的思考，對可能出現的問題準備相應的解決方法。只有這樣，當“意外”發生時才能從容不迫、應對自如。其次，教師還要有一雙慧眼，透視課堂，敏銳捕捉“意外”中有價值的信息，并合理地利用到課堂中來，靈活地進行調整，讓“意外”的課堂，不再“意外”。