登高遠望好風景，圓角關系一線牽

劉密貴

摘要：在蘇科版初中數學九年級上冊《中心對稱圖形——圓》一章中，學生認識了3種不同的“角”：圓心角、圓周角、弦切角。教學完圓的切線后，設計并實施了一節數學活動課《與圓有關的角》，引導學生整體地、系統地、一以貫之地認識“與圓有關的角”，探究它們的性質，將看似無關的知識串聯成結構體系。串聯這些知識的“金絲線”，表面的材質是點和圓、直線和圓的位置關系，產生了兩次分類;內在的材質是策略和經驗，如“先定性，再定量”“不斷轉化”“一般化和特殊化”等。

關鍵詞：與圓有關的角知識結構經驗遷移教學線索

教學機智一、初始想法：這角那角，何妨一以貫之

在蘇科版初中數學九年級上冊《中心對稱圖形——圓》一章中，學生認識了3種不同的“角”：圓心角、圓周角、弦切角。這些角的性質各有不同，使學生接受起來有些困難。其實，這些角之間有密切的聯系，而且，還有一些與它們相關的角課本中沒有涉及。這引起了筆者的思考：何不引導學生整體地、系統地、一以貫之地認識“與圓有關的角”，幫助學生建立良好的知識結構呢？于是，教學完圓的切線后，筆者設計并實施了一節數學活動課：《與圓有關的角》。

二、教學過程：對比聯系，借經驗解問題

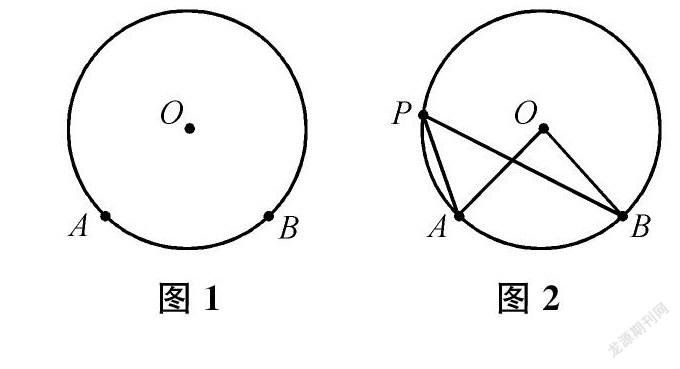
師同學們，若一個角的兩邊與圓有兩個不同的公共點A、B，則稱它是一個“與圓有關的角”。（出示圖1，板書課題）這節課我們一起來研究它。

（出示問題1：我們已經學過哪些與圓有關的角？）

生圓心角、圓周角。

師這兩種角的大小與它們所對弧的度數有什么關系？

生圓心角的度數等于它所對弧的度數，圓周角的度數等于它所對弧度數的一半。

師（出示圖2）請用符號語言分別表示∠AOB、∠APB與AB的度數的關系。

生∠AOB=mAB，∠APB=m12AB。符號“=m”在之前介紹過，表示“弧的度數等于”。

[設計意圖：學生往往憑借已有經驗，解決新的問題。圓心角和圓周角是最重要的兩種“與圓有關的角”，教師的追問暗示了本節課的重點是探究角的大小與弧的度數的關系。其實，在之前的課堂上還補充介紹過“弦切角”，但是，學生沒有馬上想到。不過，這沒有關系，后面完全可以引導學生聯想補充。]

（出示問題2：這兩種角是怎樣區分的？）

生它們的頂點位置不同，圓心角的頂點在圓心，圓周角的頂點在圓上。

師哦，頂點位置不同。我們曾經學習過點與圓的位置關系，請大家回想一下。

生點與圓有三種位置關系：點在圓上，點在圓內，點在圓外。

[設計意圖：問題1是“求同”——圓心角、圓周角都與弧的度數有數量關系，問題2是“存異”——它們因頂點位置的不同而不同。由此滲透了認識事物的異同觀。教師的追問恰到好處地聯系了舊知，為后續的問題3提供了直接經驗。如果說圓心角、圓周角等是“珍珠”，那么點與圓的位置關系就是把它們串聯起來的“金絲線”。]

（出示問題3：若不限定頂點位置，還可能有哪些類型的角？根據角頂點的位置直接命名。）

生還可能有圓內角、圓外角。

師為什么不提“圓上角”？

生已經有了，圓上角就是我們學過的圓周角。

師為什么要提“圓內角”？不是有圓心角了嗎？

生它們不一樣。圓心角是特殊的圓內角，圓內角這個說法更具有一般性。

[設計意圖：問題3是“補全”——基于點與圓的位置關系補全“與圓有關的角”的知識結構。這是一種再創造。目前，學生對“與圓有關的角”的認識從圓心角、圓周角豐富到圓外角、圓內角（含圓心角）、圓上角（即圓周角）。當然，“圓上角即圓周角”的說法有瑕疵，留待后面完善。]

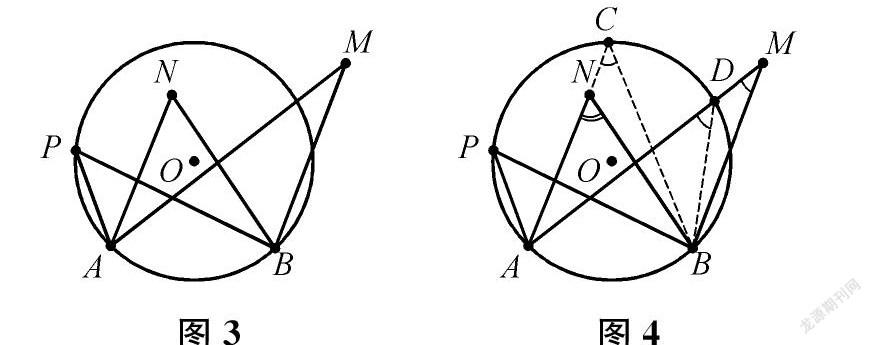
（出示問題4：圖3中有圓外角∠AMB、圓周角∠APB、圓內角∠ANB，比較它們的大小。）

生∠ANB>∠APB>∠AMB。

師為什么呢？

生（出示圖4）延長AN交⊙O于點C，連接BC，設AM交⊙O于點D，連接BD。根據同弧所對的圓周角相等可知，∠APB=∠ACB=∠ADB。因為∠ANB是△NBC的外角，所以∠ANB>∠ACB。因為∠ADB是△MBD的外角，所以∠ADB>∠AMB。綜上可知，∠ANB>∠APB>∠AMB。

[設計意圖：數學研究往往是先定性，再定量。問題4是“定性”——比較角的大小關系，是初步認知。在學習圓周角時，學生曾經探究過這個問題，所以有一定的經驗，經過回憶、思考，可以順利地解決。解決這個問題時，學生重新經歷了“連線通過外角轉化”的過程，為解決后面的問題5提供了直接經驗。]

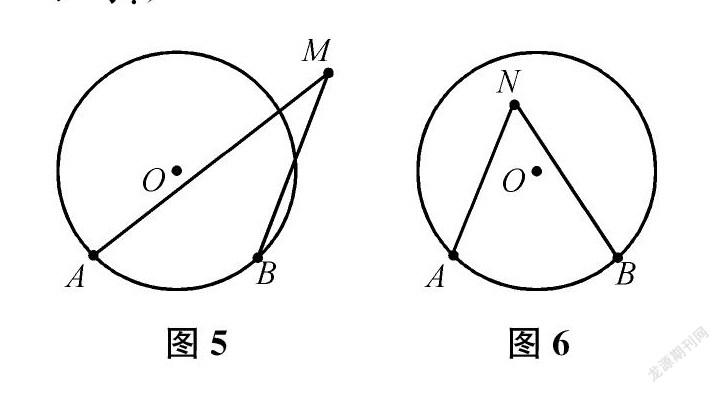
（出示問題5：如圖5、圖6，你能分別量化圓外角∠AMB、圓內角∠ANB的大小嗎？）

生老師，什么是“量化”？

師量化就是用數量刻畫，這里是指用適當的式子表示角的大小。（稍停）如果你沒有頭緒，可以試著小步子前進。以∠AMB為例，要用一個式子表示它，首先需要知道∠AMB的大小與哪些元素有關，以及怎樣將∠AMB的大小和這些元素產生聯系。如果你還想不到，想想是否有類似的經驗可以借鑒。

（學生思考、討論。）

生記∠AMB的邊與⊙O交于點A、B、C、D，則∠AMB的大小與AB、CD的度數有關。因為弧變化，角變化;弧確定，角也應該確定。跟弧有關的角有圓心角和圓周角，只要將∠AMB轉化為圓心角或圓周角，就能產生聯系了。

生可以將∠AMB轉化為兩個圓周角之差。（出示圖7）連接AC，則∠ACB是△ACM的外角，故∠ACB=∠AMB+∠CAM，從而∠AMB=∠ACB-∠CAM。由圓周角性質可知，∠ACB=m12AB，∠CAM=m12CD，所以∠AMB=m12AB-12CD=mAB-CD2。

生哦哦，我想到了！同理，∠ANB可以轉化為兩個圓周角之和。（出示圖8）連接BC，則∠ANB是△BCN的外角，故∠ANB=∠ACB+∠CBD。由于∠ACB=m12AB，∠CBD=m12CD，所以∠ANB=m12AB+12CD=mAB+CD2。

師精彩！管它圓內或圓外，全都轉化到圓周！剛才我們的探究過程，方法上是一脈相承的，即連線通過外角轉化;策略上是從定性到定量，即從模糊感受到精確制導。之前我們提到，圓心角是特殊的圓內角，那么，圓心角的大小滿足剛才得到的這個等式嗎？

生滿足！（出示圖9）當點N在O處時，恰有AB=CD，此時∠ANB=mAB+CD2=m2AB2=mAB。結果完全一致，恰好體現了圓心角是特殊的圓內角。

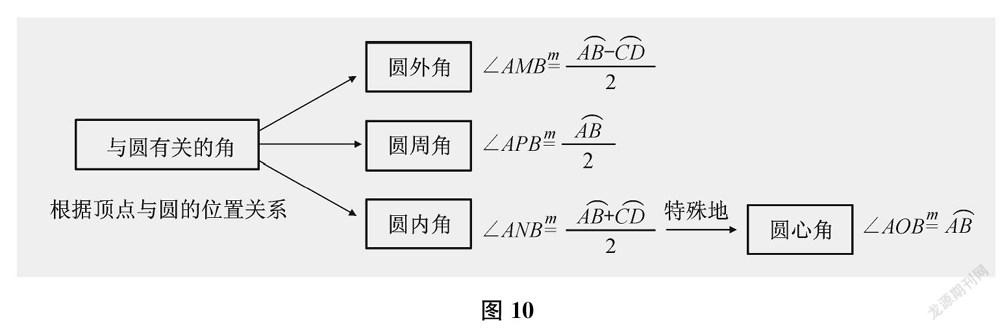
師很好，現在我們已經完成了這樣的內容：（1）根據角的頂點與圓的位置關系，將“與圓有關的角”分為圓外角、圓周角、圓內角;（2）基于圓心角和圓周角的探索經驗，量化圓外角、圓內角的大小。（出示圖10）因此，我們得到這樣的知識結構或者說思維導圖。

[設計意圖：問題5是“定量”——確定角的數量關系。“量化”是一個抽象、凝練的說法，有必要讓學生感受到其合理性。教師通過一些提示，引導學生步步深入，驀然回首，又歸闌珊。問題5沒有直接告訴學生用弧的度數表示角的大小，需要學生感受、分析和發現，這是重要的、珍貴的、不可替代的經驗。學生遇到困難時，教師對學生進行了適當的引導，這個“柳暗花明又一村”的過程是學生形成解決問題能力的必經之路。至此，學生對“與圓有關的角”的認識進一步豐滿。]

（出示問題6：從邊與圓的位置關系看，圓外角還能進一步分類嗎？）

師（再次出示圖5）圓外角∠AMB的兩邊與⊙O有怎樣的位置關系？

生都相交。

師相交是直線與圓的一種位置關系——角的邊是射線，但由于頂點在圓外，不妨看作直線，回憶一下：直線與圓有哪些位置關系？

生相交、相切和相離。

師圓外角的兩邊與圓可能有哪些位置關系？

生只可能相交或相切。

師畫出你能想到的所有可能情況。

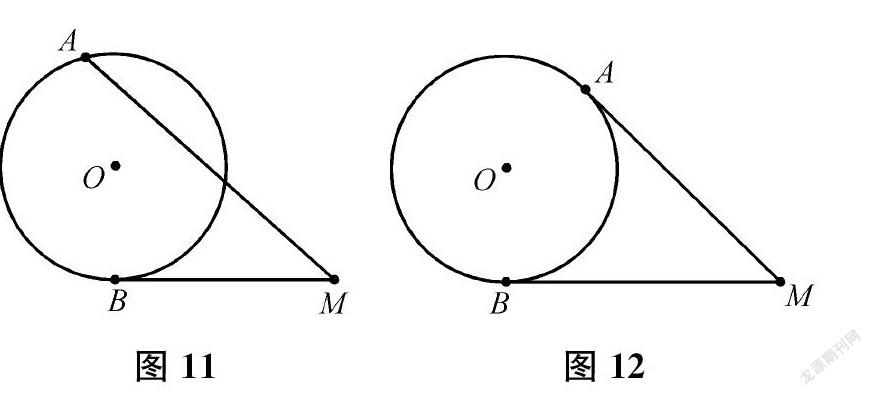
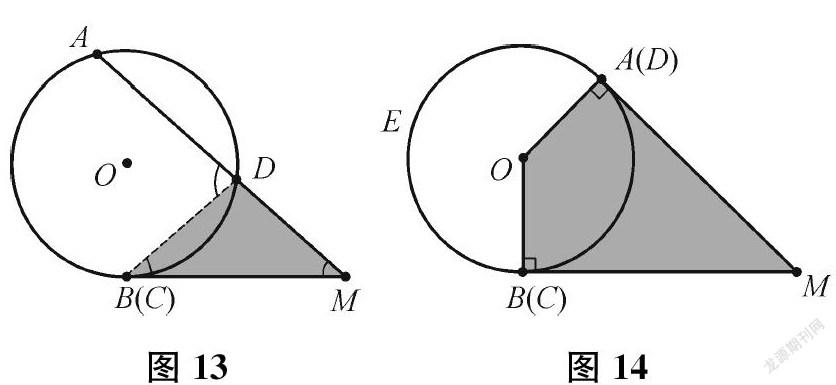
生共有3種情況：兩邊均相交，如圖5;一邊相交，一邊相切，如圖11;兩邊均相切，如圖12。

師哦，原來圓外角還有這些情況。那么，我們剛才的探索完整嗎？

生不完整。還需要補充另外兩種情況。

師那么，之前的結論∠AMB=m大弧-小弧2還成立嗎？請探索。

（學生思考、討論。）

生還成立。（出示圖13）連接BD，則∠ADB是△BDM的外角，故∠AMB=∠ADB-∠DBM=m12AB-12BD=mAB-BD2，從而成立（這里的BD其實就是CD）。（出示圖14）連接OA、OB，由相切可知∠OAM、∠OBM均為90°，易證∠AMB=180°-∠AOB。由于AEB+AB=m360°，所以∠AMB=m12（AEB+AB）-AB=mAEB-AB2，從而成立。

圖13圖14

師現在對圓外角的探索是否已經完成了？

生3種情況都考慮了，完成了。

師對圓外角，由于圖形存在多種可能，為了解決問題，需要討論每一種情況。我們是否有類似的經驗？

生有的，探索圓周角的性質時，也是根據圓心的位置將圓周角分為3種情況。

師很好！現在，我們對圓外角的探索已經經歷了兩次分類，你能說說看嗎？

生第一次是角的頂點位置，第二次是角的兩邊位置。

師既然如此，對圓內角、圓周角是否也可以從這個角度來變化？

生圓內角的邊所在直線始終與圓相交，沒有其他情況。

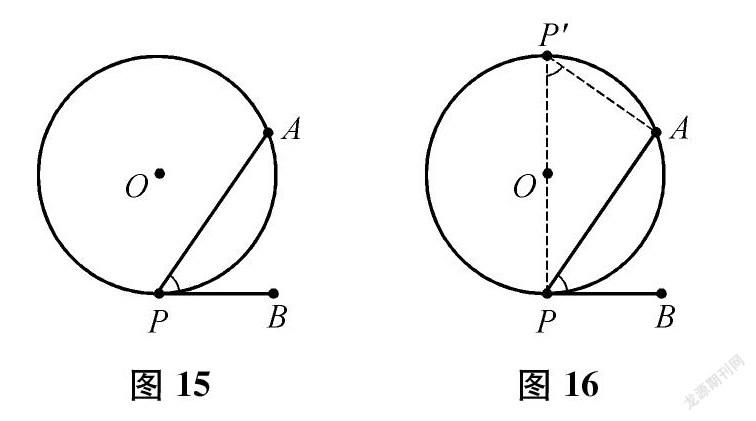
生圓周角的邊可以與圓相切或相交。如果都相交，那就是圓周角。（出示圖15）如果其中一條邊相切，那就是我們學過的弦切角。

師若圓周角的兩邊都和圓相切呢？

生那就變成一條直線了，是平角，且不是前面說的“與圓有關的角”了，就不需要研究了。

師圓周角、弦切角的頂點都在圓上，但邊與圓的位置關系不同，應該怎樣稱呼它們呢？

生可以統稱它們為“圓上角”。

師它們與所對或所夾弧的數量關系一致嗎？

生一致。（出示圖16）弦切角等于它所夾弧所對的圓周角，這個我們證明過。

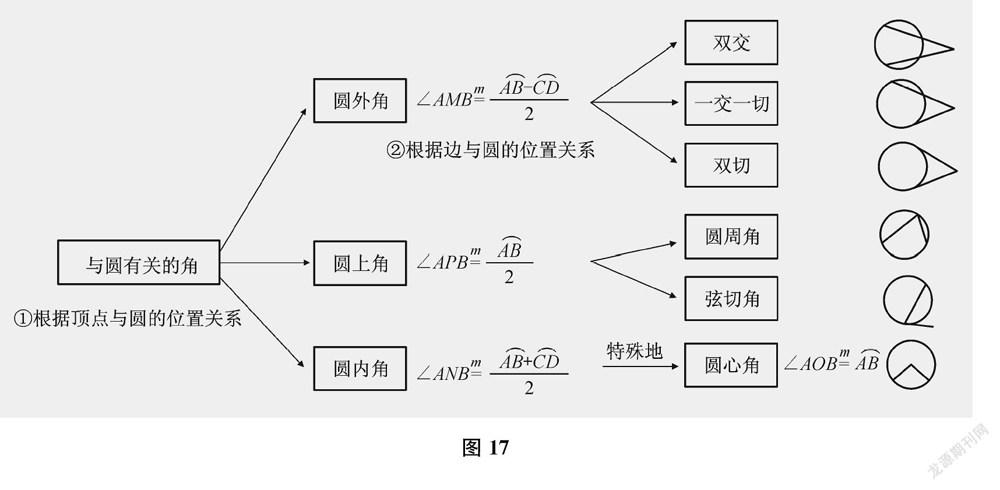
師很好！在知識結構圖上進一步補充我們的發現吧。

（師生共同完善知識結構，得到圖17。）圖17[設計意圖：兩類位置關系共同串聯起“與圓有關的角”，編織出豐滿的知識結構。問題6是再次補全——基于直線與圓的位置關系補全“與圓有關的角”的知識結構。在研究角的大小時，學生其實在不斷地轉化和借鑒，一邊積累經驗，一邊使用經驗;每一個問題都既有復習回顧的成分，又有埋下伏筆的功能——這恰是數學學習的常態。本次探索很好地將《圓》這一章的內容有機結合在一起。]

（出示問題7：你能否提煉一些通用的方法和經驗？）

生要整體地看待知識和問題，它們之間都是有聯系的。

生就像站在高處，看得清楚，居高臨下，一覽無余，我們也要從更高的角度審視數學。

生先定性，再定量！定性就像是認清方向，免得南轅北轍;定量就像找到路徑，實現順利到達。

生很多東西都是我們學過的，我們總是能把新問題轉化成我們學過的問題。

師大家說得都很好！希望同學們可以舉一反三，不斷發現數學中的美麗！

三、教學感悟：整體視角，系統感受全局

局部地看，知識是零散的;孤立地看，知識是繁多的。但整體地看，知識是一個互相聯系的結構;系統地看，知識是一個“條條大道通羅馬”的網絡。平日分課時的教學中，教師經常要求學生從微觀上掌握知識的細節，而很少引導學生從宏觀上感受知識之間的聯系。其實，登高望遠，發現知識的聯系，會更加有助于學生理解數學本質，獲得遷移能力。《義務教育數學課程標準（2011年版）》指出：“教材編寫應當體現整體性，注重突出核心內容，注重內容之間的聯系，注重體現學生學習的整體性。”數學教學中，我們更要通過整合內容讓學生感受到“整體性”的魅力。

本節課中，筆者引導學生將圓心角、圓周角、弦切角補充成“與圓有關的角”，探究它們的性質，將看似無關的知識串聯成如圖17所示的結構體系，這個過程無疑是精彩的。串聯這些知識的“金絲線”，表面的材質是點和圓、直線和圓的位置關系，產生了兩次分類;內在的材質是策略和經驗，如“先定性，再定量”“不斷轉化”“一般化和特殊化”等。本節課中，學生表現出極大的學習熱情，也讓筆者感受到“整體性”的魅力。

正是：登高遠望好風景，圓角關系一線牽，欲知其中真妙法，整體聯系如此看！